Wavelets and Multiresolution Analysis
140.02k views2530 WordsCopy TextShare

Steve Brunton
This video discusses the wavelet transform. The wavelet transform generalizes the Fourier transform...
Video Transcript:
[Music] welcome back so today I'm really excited to tell you about wavelets which you can think of as kind of a supercharged Fourier transform okay so we've already seen how you can take the Fourier transform and decompose a signal into a sum of sines and cosines into its frequency content and we've shown that those sines and cosines form an orthogonal basis for the space of functions that you want to represent and here in this wavelets lecture we're gonna see that you can generalize that idea of sines and cosines providing an orthogonal basis to other functions
orthogonal functions that might provide better representation of certain types of functions so we're going to use wavelets a lot for things like image and audio compression and really wavelets has changed how we how we compress and represent signals in the digital era okay so I'm gonna start off by talking about kind of how we think of time series Fourier transforms and the spectrogram so if you have time series data then you have this this time axis I'm just going to write these up so I have time series sometimes you can Fourier transform this data and
you get you get the Fourier transform and the idea that we've seen in the spectrogram lecture is that if I have a time series I have exquisite resolution of where my signal is in time but I know absolutely nothing about what frequency let's call this the frequency axis I know absolutely nothing about what frequencies are occurring at that moment in time so I'm going to draw that as this kind of vertical bars where I have a lot of resolution in time but I have a lot of uncertainty in the frequency similarly when you Fourier transform
say max use time frequency I know exactly what the frequency content of my signal is but I know absolutely nothing about when those frequencies occurred in time so I have a very high resolution in frequencies tons of uncertainty in where in time those frequencies occurred okay so time series Fourier transform this is what motivated us to develop the spectrogram okay so the spectrogram we saw earlier the Gabor transform spectrogram is where now we give kind of equal weighting to time and frequency and we can break this up into let's say kind of a grid where
we have maybe less time resolution that on our original time series and less frequency resolution than our Fourier transform but we know kind of when individual frequencies turn on and turn off in time so we have a little bit of time information and a little bit of frequency information okay and what I'm going to show you today this wavelet transform is going to so kind of wavelets and this is also often called multi-resolution analysis because what you're gonna see is that we're going to get multiple scales in in time and frequency in the wavelet analysis
what you have is this kind of hierarchical grading of time information and frequency information so at very very low frequencies there's this observation that low frequencies tend to last for a long time and don't change that much or that quickly over time so what we're gonna do is we're going to have a bar at the bottom which is basically the lowest frequency we don't really care when it occurs in time because we're going to assume it's on all the time okay that's kind of your baseline little frequency and then at the next level we're gonna
split this in half and we're going to get a little bit less frequency resolution but we're going to have information about you know is it in the first half of your time series or the second half of your time series and then at the next level we're gonna break this up into even more frequency resolution because at higher frequencies they change faster in time but I'll have less resolution about exactly which of those high frequencies are turning on and so this is kind of a multiscale time frequency decomposition that we're going to use the wavelet
decomposition to compute and the idea here is that the lower frequencies change more slowly in time so I don't need as much temporal accuracy and then for higher and higher frequencies I need more and more temporal accuracy but I get correspondingly more uncertainty in what exact frequency is turning on and off in that in that range and of course I only do this with three levels in reality you might have you know ten levels to this to this wavelet decomposition if you like okay and so so the the wavelet decomposition is kind of like a
really really good spectrogram that is tailored to spend as much information in the regions as necessary so low frequencies don't need as much information higher frequencies need more temporal resolution and so on and so forth so this is the wavelet decomposition okay now the idea behind a wavelet decomposition it's exactly the same as what you're used to seeing in say the Fourier decomposition or the Gabor transform we're gonna take some signal some some time series or some spatial data and we're going to project it onto an orthogonal basis but in the wavelet transform that orthogonal
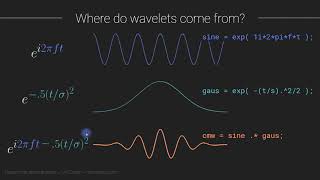
basis is not just going to be sines and cosines it's going to be kind of a hierarchy of orthogonal functions that are going to get smaller and smaller in time or in space in these little windows in time and space I'm going to write this out for you this always starts with what's called a mother wavelet so you have a kind of a mother wavelet which is basically just a shape okay and we're gonna call this some sigh of T and then from that mother wavelet you can derive all of your smaller wavelets sigh a
comma B as a function of time is going to be one over square root of a times sigh of t minus B divided by a and so you could kind of imagine if this side was something like a Gaussian then B and a what B would do is it would shift it would slide that Gaussian left or right in time so it would basically pick which window in time I'm at and a would make this wavelet bigger or smaller and make it you know a bigger a would make this wavelet smaller I guess so as
B as a increases we're going up the level so as a goes from one to two to four to eight we're going up the levels making our windows smaller and smaller and smaller and B is going to correspondingly slide that window across our our time signal okay so this is is the idea here and then what we're going to be able to do is we're going to take and we're going to say that the wavelet transform and this wavelet transform is with respect to this mother wavelet sigh of the function f and it's going to
have these two parameters a and B and it's just the inner product of our function f of T with that particular wavelet sigh a B T okay and I think it's it's probably really helpful to give you an example of what one of these these wavelets would look like so that you can picture this this wavelet transform okay so the example I want to choose is the haar wavelet which is the oldest wavelet this is I think this was around since like the 1910s I think this was introduced in 1910 and so the haar wavelet
is basically this the mother wavelet is a function that starts off at 1 and it goes down to negative 1 and that's the function it's basically just a step function plus 1 minus 1 over the whole interval that you're the whole interval that your that your wavelet transforming over okay so this is psy and I'm going to call that psy 1 comma 0 okay so it's the kind of scaled by a equals 1 so we're not making it bigger or smaller and B equals 0 so we're not shifting it at all so this is the
mother Wade lips.i 1 0 but then from this mother wavelet you can build smaller wavelets you can build the one that is in this left half that goes again from plus 1 to minus 1 only in the left half or you could also build the one that goes in the right half to plus 1 - one okay so this is the sigh let's see this is the sigh 1/2 zero okay so now I guess I said this wrong earlier so a if you make it 1/2 or 1/4 or 1/8 it makes this window smaller and
smaller and smaller so this is the 1/2 the 1/2 wavelet and this one would be the 1/2 and I'm going to shift it by 1/2 okay so and you can keep going and going and going so essentially this function here the 1 0 wavelet corresponds to this this region of the decomposition here this 1/2 0 wavelet corresponds to this portion of the decomposition here and let me maybe make blue here this 1/2 1/2 wavelet will correspond to that portion of the decomposition ok so the basic idea here and notice that these are all orthogonal functions
so if I take the inner product of this function with this I get 0 because when this is plus 1 this is half of its plus 1 and half of its minus 1 so these have an inner product of 0 similarly with with the bottom one and the top one and also the bottom two are orthogonal because they're kind of anti you know correlated this one is off this one is 0 when this one is on and the bottom one is 0 when the top one is on so all of these wavelets are orthogonal by
construction because we're basically taking this shape and we're shrinking it down into halves and if if the top shape shaped you know kind of sums up to 0 then you're gonna get this orthogonal decomposition okay and what's nice is that you can imagine kind of if this is an audio signal or if you're doing this on an image or something this big wavelet is going to pull out big structures and each of these smaller wavelets is going to pull out smaller and smaller and smaller structures in different portions of the signal in different portions of
the image or in different portions of the audio so maybe you know at some level these wavelets are gonna pull out you know the eyes on the left part of the face and the eyes on the right part of the face or something like that ok good so this is the basic idea of a wavelet it's some between a time-series and a Fourier transform it's kind of like an enhanced spectrogram where you're only putting resolution where it matters for for your signal and this is this is completely motivated by kind of natural signals that humans
care about where low-frequency stuff doesn't change that fast in time but high-frequency stuff does and so you want to put more temporal resolution at higher frequencies and more kind of frequency resolution at at lower frequencies okay so that's that's the wavelet decomposition we're gonna use this a lot for image compression so I'm going to cook up some examples where we're going to use this to compress images we're gonna do a two dimensional wavelet transform where psy is going to be a function of x and y of both spatial directions and we're going to use this
idea of these kind of shrinking and shifting wavelet transforms to compress and to represent images very very efficiently okay and I'll point out that there are hundreds of these these wavelet transforms or these mother wavelets lots and lots and lots of mother wavelets to choose from so I showed you the haar wavelet so I'm just gonna write these out there's the haar wavelets there is the dobisch ease wavelet this is named after ingrid daubechies who's one of the pioneers of this theory it's kind of a fun spiky it's a little hard to draw but this
is the dobisch ii the dobashi wavelet there's also the Mexican hat wavelet which is kind of like this I don't know why it's not called the Sun barrera wavelet but it's called the Mexican hat wavelet you can kind of see it looks like a sombrero the koi flit is basically a Mexican hat but with pointy corners it's a little hard to draw but I'll try so that's kind of like a koi foot after Ron Kaufman coil it and there's just more and more and more of these okay there are there's hundreds of wavelets that are
tuned to different data sets so maybe images you want to use dobashi wavelet or a coy flit because you know I don't know if you can see like on the black background the there's there's these sharp corners that delineate images on a background right so you might want these really sharp kind of edges and your wavelet decomposition so the the doba sheet and the coif lid are really good for that other signals you might want something smoother like a Mexican hat or a Gaussian and really you get to choose these are and we know a
lot about this there's a lot of image science of which which wavelets to use for different compressions I'll point out there are some excellent books ingrid Doba she wrote a great kind of lecture series on wavelets i think it's called ten lectures on the wavelet and also stefan millat from from paris wrote a great great book on wavelet analysis so if you want to know more there's a rich theory this this in some sense generalizes the Fourier transform it's the same exact idea of basically expanding out a function in terms of a bunch of orthogonal
functions but now we're building these functions so that they are orthogonal on this kind of hierarchical or multi-resolution domain so you have big wavelets medium wavelets and small wavelets and they're all orthogonal to each other but this this gives you kind of enhanced signal compression over just a standard Fourier transform or spectrogram okay so we're gonna play around with this for image compression but really wavelets are everywhere and you'll yeah if you if you look you'll find wavelets in lots of modern technology so JPEG the old technology used to use Fourier transforms for image compression
the new JPEG 2000 uses wavelets for image compression okay good so that's all coming up in MATLAB and in Python will code this up for image compression thank you
Related Videos

13:01
Image Compression and the FFT
Steve Brunton
48,498 views

34:29
Wavelets: a mathematical microscope
Artem Kirsanov
627,427 views
14:14
The Wavelet Transform for Beginners
Andrew Nicoll
164,301 views

45:52
Ingrid Daubechies: Wavelet bases: roots, s...
The Abel Prize
33,575 views

12:16
Fourier Series: Part 1
Steve Brunton
184,999 views

51:46
Time Frequency Analysis & Wavelets
Nathan Kutz
89,942 views

14:48
The Fourier Series and Fourier Transform D...
Up and Atom
812,212 views

46:43
Stéphane Mallat: A Wavelet Zoom to Analyze...
The Abel Prize
20,000 views

37:40
Wavelets-based Feature Extraction
Rami Khushaba
61,652 views
15:55
An introduction to the wavelet transform (...
Léo Géré
34,007 views

13:15
The Spectrogram and the Gabor Transform
Steve Brunton
63,851 views

31:38
Financial Time Series Analysis using Wavelets
VoglData
25,774 views

14:36
The Fourier Transform
Steve Brunton
138,709 views

16:28
The Laplace Transform: A Generalized Fouri...
Steve Brunton
299,454 views
46:39
Time Frequency Analysis & Gabor Transforms
Nathan Kutz
20,233 views
10:58
What is wavelet analysis
My Knowlege space
10,478 views

18:28
Terrence Tao on Yves Meyer's work on Wavelets
The Abel Prize
24,434 views
17:48
Morlet wavelets in time and in frequency
Mike X Cohen
59,618 views