O que é sazonalidade?

o Olá pessoal tudo bem com vocês nesse vídeo vamos abordar questões relacionadas à sazonalidade de uma série temporal como vimos a tendência é o importante componente de uma série de tempo além da tendência a sazonalidade também um fator que pode explicar uma parcela significativa da variável podemos definir sazonalidade como movimentos temporais regulares que ocorrem em uma variável normalmente em períodos específicos do ano esses movimentos ocorrem devido ao chamado efeito calendário e por exemplo o clima é um fator de suma importância na geração de diversos produtos agrícolas e as condições climáticas dependendo da época do ano

por essa razão a produção desses bens oscila em razão do calendário Além disso existem alguns produtos que tradicionalmente são vendidos em maior quantidade em determinados períodos do ano por questões estacionais por exemplo sorvete que é mais vendido no verão Outro fator importante na definição da sazonalidade são as preferências dos agentes por exemplo em períodos de férias ou recessos as pessoas tendem a viajar mais e a gastar mais com lazer e as instituições também podem ser citadas porque elas são que definem os feriados e outras datas que modificam o comportamento das pessoas como Natal e mais

recentemente a black friday por exemplo e veja esse gráfico novamente perceba que a períodos do ano que o comportamento da série se mostra muito acima da média e essa oscilação ocorre de forma bastante sistemática essas oscilações sejam para baixo ou para cima definir em um componente sazonal E por que é importante considerar a sazonalidade no modelo primeiro porque temos que isolar o efeito que essas tonalidades pode ter uma sede tempo caso contrário o modelo pode ser em pesado e inconsistente segundo porque é sazonalidade muitas vezes tem um papel muito importante na definição da trajetória da

sedes e por isso esse componente é objeto importante de análises e a sazonalidade pode ser estimada por meio de um modelo com dano sazonais escrevemos que a série de tempo está em função da tendência e da sazonalidade observadas mais um erro por aumente aleatório a partir disso definimos 12 danos uma para cada mês Oi aqui vemos que Y está em função de uma especificação do tempo mais do somatório das danças sazonais Beta J representam os parâmetros do efeito do tempo sobre y e os alphas são os parâmetros que definem a série em um determinado mês

e e esse quadro apresenta a estrutura dos dados quando definimos as danças sazonais por exemplo de um será igual a um se o mês analisado foi um mês de janeiro em todos os demais meses de um recebe o valor de zero já de dois recebe o valor um quando o mês correspondente a Fevereiro para todos os demais meses de dois recebe o valor zero e assim sucessivamente É sim ser hicimos todas as damas na equação o modelo não poderia ser estimado Por que teríamos um problema de multicolinearidade perfeito para evitarmos esse problema podemos optar por

duas formatações é a primeira é definir as 12 danos e exclui o intercepto da equação nesse caso os alfas mede exatamente a média histórica da variável em cada mês correspondente por exemplo alfa-1 me diria a média histórica da variável Y considerando todos os meses de Janeiro alfa-2 seria a média histórica do mês de fevereiro e assim sucessivamente No entanto quando perdemos o intercepto a reta da regressão passa na origem e isso torna a abordagem um pouco diferente o R2 por exemplo não poderia mais ser analisado ou em alternativa podemos incluir 11 da Mc manter o

Inter certo Nesse contexto os alfas medem a diferença das médias entre os períodos j e o mês base correspondente que aquele que foi omitido é uma das vantagens dessa abordagem é que a significância dos coeficientes são um teste de diferenças entre as médias dos meses correspondentes e o mês vasos nós podemos representar um modelo sazonal da seguinte forma Y = Beta 0 mais Alpha 2 de 2 + Alfa 3 de 3 mais sanan Alfa 12 de 12 o Beta 0 representa a média de y no período obtido nesse caso seria o mesmo e os demais

coeficientes são as diferenças entre a média do período base e ir no período de análise formalmente definimos a média da variável Y no primeiro mês como o valor esperado de y dado que de 2 = 0 de 3 = 0 tá na de 12 é igual a zero substituindo as variáveis islâmico zero obtemos o valor de Beta 01 e essa é uma forma muito clara de visualizar que a constante do modelo representa na verdade a média da variável Y no período que foi omitido é o segundo mês calculando dessa média como o valor esperado de

y dado que de 2 = 1 de 3 = 0 tá na de 12 é igual a zero então substituímos de 2 por 1 na equação e eliminamos os demais alimentos O resultado é que a média do mês de dois é a soma de Beta 0 mais Alpha 2 então podemos ver claramente que Alpha 2 é a diferença entre a média dos meses 1 e 2 e também é possível observar que se alfa-2 foi estatisticamente não significativa a média dos meses 1 e 2 serão iguais essa análise pode ser feita para todos os coeficientes sazonais

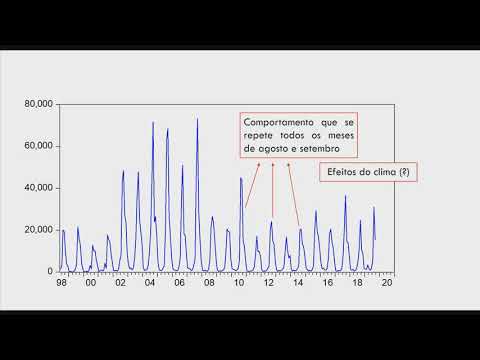
e para fixar melhor o conceito Vamos a um exemplo vamos supor que um pesquisador pretende estimar a sazonalidade da variável número de Queimadas na Amazônia entre Junho de1998 a setembro de 2019 esses dados foram retirados do Instituto Nacional de Pesquisas espaciais e veja aqui no gráfico fica evidente que em alguns períodos o número de Queimadas que estou em relação ao comportamento padrão da série essas oscilações estão concentradas Principalmente nos meses de Agosto e Setembro que são menos que historicamente apresentam baixa precipitação e a partir desses dados foi estimado um modelo com 12 danos sazonais os

resultados do modelo estão nesta tabela e as séries observada prevista residual estão plantadas nesse grupo e foi preciso da tabela são as médias históricas do número de Queimadas em cada período do ano recebemos por exemplo que em setembro aqui representada pela Thammy de 9 a média do número de Queimados foi de 32 1606 no Bioma amazônico e vamos analisar agora o braco e pelo gráfico podemos ver que a sede prevista se comporta de forma similar sair observado porém os valores estimados dos períodos sazonais Ficaram em boa parte do tempo abaixo dos valores observados perceba por

exemplo que entre 2002 e 2008 os Picos de Queimadas foram bastante superiores aos públicos estimados é isso fica evidente também se observamos os resíduos da regressão os valores acima de zero mostra o que nesse período a série observada foi de fato superior da série A Série estimado e o próprio comportamento do resido indica ainda que a informações relevantes para serem consideradas no modelo já que o erro deve ser uma variável puramente aleatório para tentar controlar esse padrão sistemático sazonal que ocorrem entre 2002 e 2008 criamos uma nova Dame especificamente para os meses de Agosto e

Setembro desse período essa Dani assume o valor 1 ciúmes era Setembro ou a gosto de 2002 a 2008 e 0 caso contrário e após controlar esse evento particular os resíduos da série passaram a se comportar de forma mais aleatório além disso a série estimada parece estar mais próxima da série observado e como podemos interpretar esses novos resultados por exemplo para o mês de agosto em média o número de Queimadas esperadas é de 15.927 é certo para o período de 2002 a 2008 nesse período particular temos que somar o coeficiente da Dame de agosto com coeficiente

da Dama e do período aquele nome nada de de 9 Alt ao somar esses parâmetros podemos inferir que a média de Queimadas de agosto entre 2002 e 2008 foi de aproximadamente 47 1842 é para Setembro Tomamos o coeficiente de 9 com o coeficiente do período específico para estimar a média de Queimadas nesse mês Nesse contexto relativo ao fazer isso a média foi de 52 1555 focos de Queimadas O que é bem superior à média desse mês nos demais anos da série analisado e no modelo com constante e vemos obtir uma dano aqui eu mentimos Adami

de Janeiro a escolha do mês é critério do pesquisador com agora temos a constante podemos analisar o R2 o modelo vemos que cerca de oitenta e sete porcento da variabilidade do número de queimadas podem ser atribuídos a fatores sazonais nesse modelo os coeficientes podem ser interpretados como a diferença entre o mês base e o mês em análises vamos analisar o coeficiente de 2 nós vemos que o coeficiente de dois foi negativo isso indica que a média histórica dos meses de Fevereiro é menor que a média dos meses de Janeiro o valor do coeficiente mostra exatamente

essa diferença podemos dizer que em média o número de focos de queimada em fevereiro é menor que Janeiro no montante de 811 queimadas ou seja Esperamos que o mês de fevereiro tem 811 queimadas a menos do que o mês de janeiro por outro lado esse coeficiente não foi estatisticamente significativo então na prática não poderíamos inferir que essas duas médias são de fato diferentes e a título de exercício tente interpretar os coeficientes dos meses de Agosto e Setembro E não se esqueça de que existe um controle específico para esses meses no período entre 2002 e 2008

esse vídeo fica por aqui até o próximo e bons estudos e E aí