Truth Table, Characteristic Table and Excitation Table for SR Flip Flop

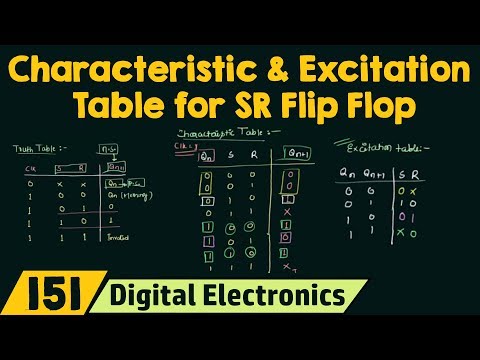
the last presentation we saw the basic off your SR flip-flop and also at the end we were having our truth table that I made here now by using this truth table in this presentation we are going to find out the characteristic table and the excitation table for s our flip-flop which is a very important part of the flip-flops and especially when you are having your flip-flop conversion so let's move to it the truth table is familiar to you in this we are having the clock whenever the clock is low whatever be the values of s

and are the QN plus 1 now let me tell you about this QN plus 1 because till now we were using Q and Q Bar actually QN plus 1 is your next state ok and QN is your present state what I mean by this is that whatever be the value stored in the flip-flop is your present state and now when your clock changes and the inputs SNR changes depending upon their values the next state will be determined ok when clock is high and s and r are 0 0 we know that it is the memory

it is the memory and by memory I mean that the next state is going to be same as the present state so the next state is QN plus 1 and the present state is Q 1 and in this case you can see that QN plus 1 is equal to Q and similarly when clock is 0 it's always the memory and by memory I mean the next state is equal to the present state QN so this is what you have to keep in your mind and similarly when clock is high SNR are 1 1 it is

invalid we don't use this configuration in SR flip-flop when s is high and R is also high so by using this information we are going to make our characteristic table first let me tell you what we have to find out in this characteristic table we have to find out the value for your QN plus 1 because QN plus 1 is your next state and next state is dependent on your input your input is s R and also the previous state so it's very clear that the inputs to this characteristic table is qn s r and

the output is q n plus 1 because i just told you that the next state is dependent on the s are the two inputs as well as the previous state so let's find out the values for QN plus 1 by using this truth table there are three inputs to it therefore eight possible combinations so let me first make it 0 0 0 0 1 1 1 1 it's a very interesting table you will find out you will enjoy evaluating the values for QN plus 1 and also the excitation table will be evaluated by using this

characteristic table so it's important now we are having the possible combinations let's try to find out the values for QN plus 1 the first case when s and R both are 0 0 we already know when SN r are 0 and I am assuming clock is high for all this operations it cannot be low indefinitely the clock is high when s is 0 R is 0 it's for memory and by memory I mean that this next state is equal to the present state so present state is what QN and QN is 0 for this configuration

so QN plus 1 is equal to Q 1 and Q n is 0 ok so this is how we have to do for a rest of the cases when s is 0 R is 1 when s is 0 R is 1 QN plus 1 is 0 so simply is 0 here when s is 1 R is 0 QN plus 1 is 1 you can see from this case and when s and R both are 1 it is invalid so I will put a cross mark here again when SN R R 0 memory and in this

case Q 1 is 1 so 2 n plus 1 is also 1 and 0 1 because s RR 0 1 1 0 and the last case is also in well because SNR r1 so you have just evaluated your characteristic table a very simple one if you know the truth table and you can see that until unless you know the values of your next state depending upon SNR you cannot evaluate your characteristic table so first remember the truth table now we will move to our next important table that is your excitation table excitation table and in

excitation table the two inputs are Q n and Q n plus 1 and the two outputs are s and R so we have to find out the values for your s and r depending upon the values of Q 1 and Q n plus 1 so let's see for the first case when both QN and QN plus 1 are 0 we have to see from this characteristic table I have already told you that the characteristic table is determined by the truth table and the excitation table is determined by the characteristic table and that's why the truth

table is the basic block for this tables so QN is 0 for this two cases and also QN plus 1 is 0 for this two cases and I can see that the value of s is always 0 so I can write as equal to 0 but the value of R is 0 1 so I can write cross that is our is our don't care now let's see when Q n is 0 and QN plus 1 is 1 so I will do it in different color here Q n is 0 Q 1 plus is 1 and

in this case s is 1 and R is 0 so s is 1 and R is 0 now let's move to the next case when a QN is 1 and 20 plus 1 is 0 and for this we are having this case Q n is 1 and QN plus 1 is 0 and this s is 0 and R is 1 so s is 0 R is 1 and for the last case when Q and and QN plus 1 R 1 which means in this case and also this case the green ones in this are is

always zero you can see but s is changing from 0 to 1 so s is our don't care and our is zero so this is our excitation table you need to remember this thing because you are going to use it frequently in the flip-flop conversions and also in the counters so just remember these things they are very important one more thing that you have to do here is to find out the value of Q and plus one so how you are going to do that you are going to make it cell k-map because three inputs

are there so we are having a itself key map let me make it and in this eight cell K map you are having your inputs as qn s are 0 0 0 1 1 1 1 0 0 1 here now let's fill this K map for Q 1 plus 1 0 0 1 Cross 1 0 1 cross ok now let's do the pairing my first group is this combining 2 don't cares and 2 ones I will call it 1 and my second group is this one okay and I will call it - so let's find

out what is the value of Q n plus 1 it is 1 or 2 so from the first group I'm having what s because R is changing from 1 to 0 and QN is also changing from 0 to 1 so it is s and from the second group I'm having QN and s is 0 and it is 1 and R is 0 and remains 0 so s will be neglected and I'm having our complement so this is the value for QN plus 1 similarly you can find out the values for s and R do it

by yourself and this is all for the characteristic table and the excitation table of SR flip-flop when we do the flip-flop conversion and designing of the counters you will find out that how these tables are used so see you in the next presentation when we will discuss the D flip-flop