Redes Neurais - A arquitetura da rede Multilayer Perceptron
2.39k views3197 WordsCopy TextShare

UNIVESP
Nesta videoaula, o professor Marcos G. Quiles irá apresentar a arquitetura base da rede MLP e a impl...
Video Transcript:
[Música] Olá bem-vindos à sétima aula do curso de redes neurais Eu sou professor Marcos killes e na aula de hoje nós vamos aprender sobre os modelos mais importantes dessa área que é o modelo Multilaser mlp nós vamos lembrar Recordar um pouco das limitações modelos Linhares apresentar como funcionam como arquitetura dessas redes de múltiplas camadas estão organizadas como a gente interpreta o problema chora a partir da solução utilizando redes com multiplas e apresentar por fim algumas topologias alternativas da rede Multilaser o que que o problema chora diferente do Problema Hora do problema end que nós abordamos
as aulas anteriores que podem ser resolvidos utilizando uma fronteira de separação linear no problema chore nós temos que o padrão 00 representa pra gente a classe 0 o padrão 11 representa a classe zero e o padrão 0110 representam a classe 1 ou seja não tem como passar uma reta nessa nessas regiões aqui separando o que é Classe 1 do que a classe zero então precisa de uma superfície de separação não linear assim como essa elipse que está desenhada aqui Então como que a gente pode resolver isso a gente sabe que a gente não consegue resolver
com o neurônio apenas porque ele só resolve portas lineares então o que que nós precisamos fazer para resolver esse tipo de problema primeiro assumindo redes com apenas uma camada a gente está restrito a solução de problemas nas quais a fronteira de separação vai ser sempre uma reta um plano dependendo da dimensionalidade do problema quando nós acrescentamos redes com múltiplas camadas nós podemos resolver essa limitação e como o contexto histórico como nós já vimos na aula sobre história das redes neurais artificiais o desenvolvimento algoritmo da propagação que foi proposto para treinar essas redes muito pelas camadas
foram um dos Marcos na década de 80 e responsável pelo surgimento do interesse pela pela área de redes neurais após o inverno da década de 70 Qual que é a questão não adianta apenas utilizarmos redes com múltiplas camadas se nós não utilizarmos funções de ativação adequada por exemplo se nós tivermos redes com múltiplas camadas que utilizam funções lineares esse problema pode ser emulado por uma rede com uma única camada Ou seja a rede com múltiplas utilizando saídas lineares vai funcionar de certa forma como uma rede com uma única camada linear Vamos pensar esse exemplo simples
aqui onde nós temos a saída y1 do neurônio 1 é o X1 vezes o W1 então X1 vezes W1 a gente tem a saída 1 do neurônio essa saída alimento o segundo neurônio então a saída desse segundo neurônio é o y vezes W2 então nós temos dois neurônios representando duas camadas primeiro camada oculta segundo camada de saída a saída do neurônio N1 é X1 xw1 a saída dorme 2 é o y1 x W2 só com y1 que tá aqui nós sabemos calcular ele de maneira explícita então substituindo esse y1 pelo valor X1 W1 nós chegamos
que Y2 = X1 vezes W1 vezes W2 Aqui nós temos duas constantes multiplicando W1 com W2 nós podemos gerar um WC ou seja nós podemos calcular o Y2 a partir da multiplicação de X1 vezes WC diretamente a partir de entrada então não precisa Nós não precisamos passar por duas camadas essa rede com duas camadas lineares ela pode ser simulada por uma rede com uma única camada linear então portanto nós precisamos de função de ativações funções de ativação não linear para introduzir na rede essa capacidade de resolver problemas não lineamente separadas Então tá aqui nosso neurônio
CP que nós veremos diversos visa ao longo do curso aqui a diferença é que eu não tô colocando um teto explícito ou seja não tô colocando a função degrau tô falando o seguinte o campo local induzido V é o produto interno do vetor x pelos respectivos pesos gerando V esse V ele vai passar por uma função de ativação definida aqui por fim e essa funcionativação ela pode assumir diversas formas por exemplo a gente pode pensar numa ativação é do tipo degrau uma função sigmoide uma função tangente parabólica a gente vai ver algumas delas ao longo
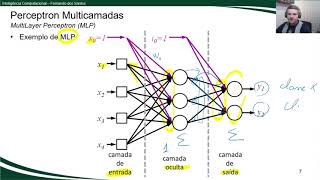
dessa aula então aqui da arquitetura da nossa rede Multilaser a gente tem a nossa entrada nesse caso aqui representada por cinco dimensões cinco padrões a primeira camada oculta ou também chamada de camada escondida uma segunda camada oculta também chamada de camada escondida então a gente pode ter múltiplas camadas entre a entrada e a camada de saída e por fim uma camada de saída que vai ser aquela que vai apresentar o resultado do problema resolvido pela rede é Cuidado que na literatura nós temos alguns autores que falam que essa daqui é uma rede com três camadas
porque ela tem três camadas de neurônios ajustáveis porém alguns autores falam que essa é uma rede com quatro camadas porque ela tem a camada de entrada e três camadas ajustáveis eu prefiro falar três camadas porque nós temos três camadas nas quais nós podemos ajustar os parâmetros dos neurônios bom então funciona ativação Como já tinha comentado nós temos diversas desde uma função linear que é limitada resolver lineares lineamente separáveis função degrau a função sigmoide tangente pebólica função reluca ela é muito utilizada atualmente função soft Max utilizada como uma camada softmax para a classificação de dados e
dentro diversas outras que nós podemos encontrar na literatura então aqui tá um exemplo primeiro a função linear nada mais é do que f de x = x então Campo local induzido ele vai ser fornecido como saída da rede a gente não tem nenhum tipo de modificação nesse sinal já a função degrau é uma função Não linear que fala o seguinte se o campo colocar induzido for maior do que zero a saída é um senão ela é zero a função sigmoide logística já é uma função contínua que vai de 0 até 1 então com essa função
a gente consegue representar o que a gente chama de neurônios frequenciais Ou seja aquele neurônio que ele tá no estado de repouso sai da Zero aquele neurônio que tá com uma saída 1 indicando um neurônio biológico ou analogia neurônio biológico com saída de ativação máxima capacidade para o máximo mas também a gente pode representar um degradê entre 0 e 1 por exemplo 0.5 a gente poderia distrair como sendo um neurônio representando um neurônio representando neurônio biológico com 50% da sua capacidade de disparo e aqui embaixo nós temos a derivada dessa função de ativação sigmoide logística
a segunda função tangente perbólica função é contínua né a tangente parabólica ela é equivalente a função sigmoide logística porém o intervalo dela vai de -1 e 1 ela é antimétrica e a derivada dela Segue o mesmo comportamento da função sigmoide ela é bastante utilizada também principalmente em redes recorrentes que a gente vai ver mais para frente aqui a função relu ela também é uma função no linear só que ela é mais simples se o valor do campo localizado for menor igual a zero ela é zero se não é o próprio valor x a vantagem dessa
função é que a derivada na fase positiva ela é constante ela é sempre igual a 1 então a gente não tem diferente da tangente hiperbólica da sigmoide logística o desaparecimento do Gradiente é para valores muito distantes da origem a gente sempre é uma derivada constante a gente sabe que é derivada vai ser importante para fazer a atualização dos pesos os parâmetros dessa rede e a função softmax ela é uma função utilizada para classificação basicamente a gente vai transformar a saída a saídas de um de uma rede e uma distribuição de probabilidade então o que que
vai acontecer com esse caso nós temos que a saída de um neurônio qualquer vai ser a exponencial do campo local induzidores neurônio dividido pelo somatório da exponencial do campo local induzido de todos os outros neurônios essa camada de saída como consequência eu somatório dessas saídas da camada softmax vai ser sempre igual a 1 então se eu tenho três saídas representando um problema de três classe por exemplo se eu tenho que sair da um Ela É 0.8 eu sei que a soma das saídas da do neurônio 2 e 3 vai ter que ser igual a 0.2
para somar para totalizar um e essa forma dá Exatamente isso para a gente bom retomando o problema chora nós vimos que ele é um problema que eu não consigo resolver utilizando uma fronteira de separação linear utilizando uma rede linear Então como que a gente pode utilizar uma rede múltiplas camadas para resolver esse problema eu quero criar essa Fronteira não linear aqui mas a cada neurônio resolve apenas uma fronteira de separação linear então utilizando múltiplas camadas a gente consegue resolver esse problema eu vou mostrar isso para vocês nesse exemplo aqui eu tenho uma rede com dois
neurônios na camada oculta e um neurônio de saída e o que que eu tô falando essa rede como um todo ela vai receber o X1 e X2 suas entradas e vai fornecer aqui na saída os valores desejados por padrão 00 e um um A gente vai ter uma saída zero e quando a gente tem apenas uma das duas entradas ligadas seja X1 ou X2 a gente vai ter uma saída um indicando a classe 1 bom então o que que esses neurônios representam né se a gente pegar o primeiro neurônio da rede neurônio N1 e analisar
só o conjunto de pesos dele a gente tem que o bayers é menos 05 eu tenho o primeiro peso associado um e o segundo peso associado ao neurônio a entrada 2 É também um então o que que esse neurônio resolve para a gente Primeiro vamos calcular o campo local induzido dele que é o somatório das entradas ponderada pelos pesos a gente pode observar o seguinte o campo localizado Vai ser 1 x - + X1 vezes o peso 1 + X2 x 2 que é o que tá representado aqui nessa equação substituindo os valores para o
primeiro caso onde nós temos entradas 0 e entradas zero eu tenho que y1 a saída desse neurônio 1 vai ser então menos 1.5 + 0 - 5 como esse valor é negativo a saída do neurônio é zero Então a gente tem que o primeiro a saída do primeiro neurônio O primeiro exemplo vai ser igual a zero como está indicado aqui na tabela se a gente pegar o segundo exemplo onde agora eu tenho o X2 = 1 então o que que a gente vai ter o menos um e-mail do baias + 0 porque o X1 =
0 e mais um vezes um porque eu tenho peso 1 vezes a entrada um fornecida pela rede aqui eu vou ter então um menos um e meio ainda tem um valor negativo de menos meio logo a saída também é zero e a mesma coisa vale se eu tivesse o X1 = 1x2=0 também teria um valor de menos meio e a saída também seria 0 então a gente tem que a saída para esses dois casos aqui também é zero por outro lado quando eu tenho tanto X1 quanto X2 ativos então vou ter menos um meio mais
um mais um Eu tenho dois menos um e meio eu tenho o valor de meio positivo logo a saída é igual a um então apenas para o padrão um e um a gente tem uma saída do neurônio igual a 1 Só que nós sabemos que a porta do tipo Wendy que nós já resolvemos ela nas aulas anteriores então o que que essa porta representa né ela representa para a gente uma porta end um relógio 2 que que ele vai representar Observe que a ele tem exatamente o mesmo conjunto de pesos porém o baias do neurônio
era um e-mail o Bayer como consequência toda vez que eu tiver apenas Uma das entradas ou as duas entradas ativas esse neurônio vai responder com saída 1 por quê Porque a hora que eu faço somatório menos meio mais um ou mais um ou mais dois a gente vai ter um valor positivo Então essa função ela só vai ter um valor negativo representando a saída zero quando tanto X1 quanto X2 forem positivos forem iguais a zero Então como consequência a gente tem a seguinte saída para o neurônio n2 que é uma saída Zero Apenas quando os
dois forem nativos e uma saída um quando eu tiver pelo menos uma das entradas ativas com valor um Então esse segundo neurônio vai responder para a gente como sendo uma porta lógica do tipo ó ou lógico bom então nós sabemos o que que o neurônio representa e o que que neurônio 2 representa essa porta Angel ou seja essa reta essa Fronteira de separação abaixo da reta classe zero acima da reta classe 1 o neurônio 2 representa essa segunda reta aqui acima da reta classe 1 os 3 padrões e abaixo da reta classe 0 o que
que neurônio 3 representa primeiro lugar o neurônio 3 O que que ele recebe como entrada Ele não recebe X1 e X2 ele recebe as saídas dos neurônios N1 e dos neurônios n2 assim como qualquer neurônio ele também vai resolver uma fronteira de separação linear mas eu sei que eu tenho um problema na linear Então por que que ele tá resolvendo problema primeiro fato como eu já falei ele não tá recebendo x1x2 ele tá recebendo a saída de N1 n2 que são essas duas colunas que foram geradas por essa camada oculta então basicamente N1 n2 eles
transformaram aquele problema X1 X2 num outro problema representado por Y2 logo o neurônio 3 ele vai criar uma fronteira de separação sobre essa nova configuração do problema sobre essa nova representação do nosso problema então se nós plotarmos os valores de y e Y2 no nosso passo euclidiano aqui eu tenho zero zero tá aqui classe 0 0 1 que são as duas linhas subsequentes vai ser 01 que é classe 1 e o padrão 1 1 também é classe 0 ou seja um probleminhamento separado eu consigo separar com uma reta que é exatamente o que esse neurônio
que está fazendo ou seja sempre que eu tiver a saída Y2 ativa eu vou ter um mais menos meio então vou ter um valor positivo a classe vai ser um e quando o Y2 for 0 ou quando Y um Y2 for com Y2 for zero ou quando Y2 for 1 associado ao Y também 1 a gente vai ter um valor negativo indicando a classe zero para esses dois casos que é o que tá aqui abaixo dessa reta ou seja o neurônio N3 ele resolve para a gente o problema chora mas ele não resolve o problema
chora a partir das entradas originais ele resolve a partir de uma representação criada pela camada oculta representada pelos neurônios N1 e n2 então o que que a rede mlp faz como um todo primeiro camada camada ela vai transformar um problema original num segundo problema a partir da saídas dos neurônios da primeira camada oculta essa saídas ou essa nova representação criada pela primeira camada oculta vai alimentar uma próxima camada que vai alimentar uma próxima camada Até chegar na camada de saída então o que que a gente está fazendo passo a passo a gente tá transformando um
problema difícil um problema que não linearmente inseparável impossivelmente um problema que lá na penúltima camada ele se transforma num problema lineamente separável a partir dessas múltiplas transformações das representações permitindo que apenas um neurônio ou um conjunto de neurônios na camada de saída que só criam Fronteira separação linear possam resolver esse problema algumas topologias alternativas da rede MP como nós vimos até então a rede mlp é formada pela camada de entrada que alguns autores consideram ou não como uma camada como eu já comentei e uma sucessiva sequência de camadas ocultas e a camada de saída sendo
que a cada camada ela alimenta cada neurônio de uma da camada alimenta todos os neurônios da camada posterior só que a gente pode ter topologias alternativas por exemplo as representadas aqui nesses gráficos onde as entradas alimentam os neurônios da primeira camada mas também alimentos neurônios da segunda camadas da terceira camada a partir do que a gente chama de sinais residuais esse artigo apresentado nesse link aqui ele faz uma abordagem bastante interessante sobre essas topologias alternativas da rede Multilaser Qual que é a vantagem dessas abordagens alternativas nós conseguimos representar ou resolver problemas um problema específico utilizando
uma quantidade menor de neurônios a utilizar essas conexões residuais essas abordagens não não triviais como consequência ao ponto mais crítico disso é que a estrutura de dados que representa essa rede já passa a ser uma estrutura não trivial em comparação a arquitetura tradicional onde nós temos cada camada alimentando todos os neurônios da próxima camada sem as ligações residuais então aqui eu trago para você só para mostrar que é possível a gente configurar a conexão entre os neurônios de mandar da camada com uma outra camada da rede Multilaser não apenas com aquela conexão densa que a
gente faz camada camada todo mundo alimentando todo mundo mas também a partir dessas conexões residuais no qual uma entrada por exemplo pode alimentar um neurônio da primeira da segunda da terceira camada e a saída de um dado neurônio pode alimentar não apenas a camada posterior mas todas as camadas posteriores ou um conjunto de camadas posteriores então o que que nós vimos nessa nessa vídeo aula nós entendemos as limitações das redes como a única camada nós sabemos que uma ritmo a única camada só consegue resolver problemas e uma rede com múltiplas camadas utilizando função de ativação
linear também só vão resolver problemas Porém quando nós agregamos múltiplas camadas utilizando funções de ativação não linear nós conseguimos criar representações intermediárias passo a passo camada camada de tal forma que a gente chega na penúltima camada da rede ou na camada de saída da rede é transformando aquele problema original que ela não lineamente separado num problema que passa a ser lineamente separado ou mais próximo de um problema lineamente separado então nós conhecemos a rede mlp nós vimos como resolver o problema choro utilizando essa rede entendemos como o que que cada neurônio da camada oculta representa
nesse caso bom na próxima aula nós vamos aprender sobre algoritmo de reto propagação Beck propagation que é o Como já foi mencionado na no histórico das redes neurais é um algoritmo dos mais importantes da literatura e acarretou o re interesse pela área de regionais na década de 80 Então nós vamos entender como ele funciona e a derivação dele como a gente calcula a atualização de cada peso da rede a partir da retropropagação dos erros obtidos na camada de saída bom Agradeço a todos pela atenção e até a próxima vídeo aula [Música] [Música]
Related Videos

20:30
Redes Neurais - Fundamentos e derivação do...
UNIVESP
2,108 views

14:29
Como uma Rede Neural Aprende? Tutorial par...
Escola de Inteligência Artificial
79,258 views

1:16:13
RNA - Redes de Múltiplas Camadas (MLP)
Prof. Dr. Petronio Silva
257 views
9:54
Redes Neurais: Conceito de MultiLayer Perc...
Fernando dos Santos
6,520 views

14:55
Por que o CHOCOLATE FICOU TÃO RUIM?
Olá, Ciência!
368,417 views

34:48
The Unreasonable Effectiveness of JPEG: A ...
Reducible
1,093,060 views

18:19
Por que o BRASIL não tem TRENS?
Ciência Todo Dia
586,494 views

9:33
Pro-Israel lawyer laughed at by British po...
Declassified UK
210,794 views

17:56
Ukraine peace deal fractures over unworkab...
Times Radio
176,827 views

15:56
10.4: Neural Networks: Multilayer Perceptr...
The Coding Train
325,586 views

10:42
‘He’s been exposed’: Tesla flounders as El...
MSNBC
476,143 views

30:30
‘Trump chickened out’: Chinese social medi...
CNN
682,222 views

3:01
Mateta STUNNER but Palace draw at Arsenal ...
Sky Sports Premier League
812,390 views

2:28:58
Shaolin Warrior Monk: Hidden Epidemic Nobo...
The Diary Of A CEO
97,735 views

11:54
Lawrence: China sees 'world's biggest clow...
MSNBC
1,148,658 views

2:25:27
Former FBI Agent: If They Do This Please R...
The Diary Of A CEO
949,705 views

20:02
Best Sports Fails | Dumb Athletes
FailArmy
334,317 views

11:51
Trump's Crimea gamble crumbles as Zelensky...
Times Radio
38,581 views

10:18
VIDA EM OUTRO PLANETA? A DESCOBERTA MAIS I...
Ei Nerd
863,356 views

42:54
Redes neurais e multilayer perceptron - Au...
Diogo Cortiz
18,119 views