A melhor explicação de Recursividade do Youtube

na programação a recursão pode ser definida como uma função que chama ela mesma É como se você tivesse um sonho dentro de um sonho ou como uma boneca russa onde você precisa abrir todas as bonecas uma dentro da outra até chegar na menor de todas e depois você faz a mesma coisa de trás para frente para voltar elas no formato original para entender a função recursiva primeiro a gente precisa entender a diferença entre a função iterativa e a função recursiva a função interativa é uma função que usa o loop como o for ou I para

repetir uma série de instruções até que uma certa condição seja atendida por outro lado a função recursiva é uma função que chama ela mesma até uma condição ser atendida ou seja ela divide o problema principal em problemas menores e no final é como se ela juntasse todos os resultados dos problemas menores para retornar ao resultado do problema principal eu sei que só falando assim vai ficar difícil de entender então eu vou te dar um exemplo prático vamos supor que a gente precisa criar uma função em JavaScript que calcula o fatorial de um número se você

você não sabe Na matemática o fatorial é representado por um número positivo seguido por um ponto de exclamação e o resultado do fatorial é a multiplicação de todos os números positivos de 1 até n ou seja o fatorial de 5 seria 5 x 4 x 3 x 2 x 1 que vai ser 120 E o fatorial de 3 seria 3 x 2 x 1 que vai ser 6 Então a gente vai criar essa função que calcula o fatorial das duas formas a iterativa e a recursiva Assim fica mais fácil de você você entender a diferença

entre elas na forma iterativa a gente vai criar a função fatorial que vai pegar n como argumento e dentro dela a gente vai criar uma variável resultado com valor de um porque esse é o valor mínimo que o fatorial pode ter e agora a gente vai criar o loop for da função então enquanto o contador I for menor ou igual ao número que a gente quer calcular o fatorial o loop vai continuar e dentro desse loop a gente vai multiplicar o valor do resultado pelo próximo número da Contagem ou seja se a gente pedir pra

função calcular o fatorial de 3 esse loop vai fazer multiplicação de 1 x 2 x 3 que vai retornar o resultado 6 essa é a função iterativa que você provavelmente já usou diversas vezes agora para criar a função recursiva a gente vai começar de novo criando a função fatorial que pega n como argumento só que agora a gente vai começar criando uma condição onde se n for igual a 1 ou igual a z0 a função vai retornar 1 mas agora se n for maior do que 1 a função vai retornar n multiplicado pela própria função

só que dessa vez levando n - 1 como argumento ou seja se a gente quiser calcular o fatorial de 5 a função vai verificar 5 = 1 não então ela vai retornar 5 x fatorial de 4 isso vai chamar a função de novo mas dessa vez com fatorial de 4 que vai retornar 4 x fatorial de 3 o fatorial de 3 vai retornar 3 x fatorial de 2 o fatorial de 2 vai retornar 2 x fatorial de 1 e por fim o fatorial de 1 vai retornar 1 o fatorial de um é o que a

gente chama de caso base porque que é ele que coloca um fim no loop da função sem o caso base a função recursiva iria entrar em um Loop Infinito E isso não seria muito bom pro seu computador então quando a função recursiva chegar no fatorial de 1 e retornar um esse resultado vai ser usado para completar o fatorial de dois que tinha ficado pendente na memória do computador então agora o fatorial de do vai conseguir a resposta que vai ser 2 x 1 que é 2 com isso o fatorial de 3 também vai conseguir se

completar resultando em 3 x 2 que é 6 com o resultado do fatorial de de 3 vai ser possível completar o fatorial de 4 que era 4 x fatorial de 3 ou seja 4 x 6 resultando em 24 e por fim com o resultado do fatorial de 4 o fatorial de 5 que foi o problema que a gente queria resolver desde o começo Vai resultar em 5 x fatorial de 4 ou seja 5 x 24 que vai ser 120 E é assim que a função recursiva funciona ela basicamente divide o problema em diversas partes e

depois junta tudo para retornar à resposta do problema Inicial É como se você quisesse pegar água do poço você começa com um balde na superfície e tem que baixar ele até o fundo do poço passando por todo o percurso e lá no fundo você pega água que nesse caso seria o caso base da função recursiva e então você traz o balde para cima de novo fazendo todo o caminho de volta até que o balde retorna cheio de água ou seja com o resultado esperado toda função recursiva tem duas partes obrigatórias A primeira é o caso

base que é onde a gente vai dizer pra função quando ela deve parar o caso base é muito importante porque é ele que vai impedir que a função fique rodando infinitamente e a segunda parte que é a chamada recursiva Essa é a parte da função onde ela chama ela mesma Ou seja é isso que torna a função recursiva então só para lembrar na nossa função recursiva que Calculava o fatorial a condição que verificava se n Era Zero ou 1 seria o caso base e a parte que retornava n ve fatorial de n - 1 seria

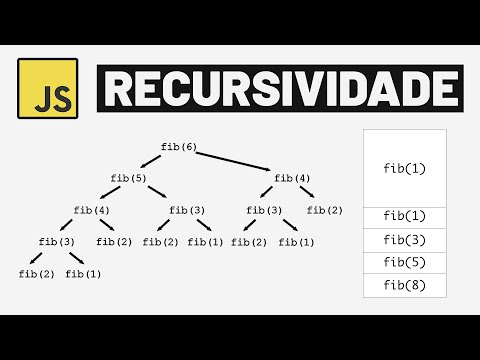
a parte da chamada recursiva agora que você já entendeu melhor como a função recursiva funciona a gente pode ir para um exemplo mais famoso em que a recursividade também pode ser aplicada a sequência de Fibonacci a sequência de Fibonacci é uma sequência de números onde cada número é a soma dos dois números anteriores a sequência começa com 0 e 1 e segue assim 0 + 1 1 1 + 1 2 1 + 2 3 e assim por diante a sequência de Fibonacci é interessante porque ela aparece em muitos lugares na natureza como nas flores nas

amif das Árvores no formato das galáxias e até na Monalisa é um conceito matemático simples mas que tem muitas aplicações práticas na programação então para criar uma função recursiva de Fibonacci a gente vai começar incluindo p como argumento da função onde P vai ser a posição de Fibonacci que a gente quer descobrir ou seja se P for 5 a função tem que retornar o quinto número da sequência que é 3 agora a gente vai criar uma condição que verifica se p é igual a 1 Se esse for o caso a função retorna Zero Isso porque

o primeiro elemento da sequência é zero agora se esse não for o caso e p for igual a 2 a função vai retornar 1 já que esse é o segundo elemento da sequência ou seja essas duas condições vão ser os casos base da função recursiva Agora falta a gente criar a chamada recursiva e é aqui que as coisas vão ficar mais complicadas a função vai retornar Fibonacci de p - 1 mais Fibonacci de P - 2 O que isso quer dizer é que a função vai retornar a soma dos dois números anteriores da sequência E

é exatamente isso que a gente quer então se a posição da sequência que a gente quer descobrir for TR por exemplo a função vai perguntar 3 é igual a 1 não 3 é = 2 não então retorne Fibonacci de 3 - 1 mais Fibonacci de 3 - 2 ou seja retorne o número na posição 2 mais o número na posição 1 da sequência de Fibonacci isso vai chamar função de novo só que dessa vez P vai ser 2 e 1 então em Fibonacci de 2 a função vai perguntar 2 é iG 1 não 2 é

iG 2 sim então a função vai retornar 1 já no caso do Fibonacci de 1 a função vai perguntar 1 é ig a 1 sim então retorne zero e essa é a mágica dos casos base então voltando paraa Fibonacci de3 onde a função tinha chamado Fibonacci de 2 e Fibonacci de 1 a Fibonacci de 2 vai retornar 1 e a Fibonacci de 1 vai retornar zero agora é só somar 1 + 0 que vai ser 1 ou seja o número da terceira posição na sequência de Fibonacci é um Agora se a gente quer saber Fibonacci

de c Por exemplo a Fibonacci de 5 vai chamar as funções Fibonacci de 4 e Fibonacci de TR a Fibonacci de 4 iria chamar Fibonacci de TR e Fibonacci de 2 e assim por diante até chegar nos casos base onde as funções de Fibonacci de 1 ou dois vão ser chamadas e vão retornar zero e 1 respectivamente E então as respostas das funções com o caso base vão completar todas as funções que estavam pendentes de trás paraa frente Até voltar pra função Fibonacci de 5 que vai retornar três ou seja quando você usa uma função

recursiva ela vai chamar ela mesma repetidamente até chegar nos casos base que você definiu ou seja ela vai criando várias cópias dela mesma e enquanto não chegar nos casos base as funções que foram chamadas vão ficar pendentes na memória então basicamente as diferenças entre a função iterativa e a recursiva São que na grande maioria dos casos a função recursiva tende a ser mais lenta já que ela acaba criando várias cópias dela mesma de certa forma isso acaba consumindo mais memória que a função iterativa e consequentemente deixando seu programa mais lento já a vantagem da função

recursiva seria que em alguns casos ela pode simplificar e fác a compreensão de um problema sendo assim em geral as funções iterativas são mais eficientes porém mais complexas e as funções recursivas em geral são mais lentas porém mais simples de escrever