Modelos autorregressivos (AR) - propriedades de média e variância
2.64k просмотров2198 СловКопировать текстПоделиться
economiaetv
➡️ CONSULTORIA, ASSESSORIA ACADÊMICA E PARCERIAS: economiaetv@gmail.com.
➡️ CURSO: INTRODUÇÃO A MOD...
Транскрипция видео:
o Olá pessoal tudo bem no vídeo de hoje a gente vai falar um pouco sobre os processos autoregressivos a gente vai abordar as propriedades de média e variância EA gente vai tentar entender como que essas propriedades podem ter relação com a condição de estacionariedade da série modelos autoregressivos são aqueles em que uma variável é gerado por um processo estocástico estacionário que contém os valores passados a gente pode representar um processo auto-regressivo por y t = fiz um yt menos um mais fi 2yt menos dois mais FIPE yt - p mais é ter que é o
nosso termo de erro B é a ordem desse processo e Assumimos que o erro do modelo tem média zero variância constante igual a Sigma 2G e covariância é igual a zero para todo ter diferente DS TS aqui são os períodos do tempo bom então dizemos que um processo auto-regressivo de uma variável estacionária no período T pode ser representado por uma função de seus valores passados mais de um termo de e puramente aleatório e o processo auto-regressivo também pode ser representado por meio de operador de defasagens primeiro Vamos colocar todos os elementos que contém Y do
lado esquerdo da equação depois vamos substituir os termos defasadas de y pelos seus respectivos operadores e defasagem por exemplo lyt é o termo que representa yt - 1l 2yt é o termo que representa e y tem menos dois elyt é o componente que se refere a expressão YP - p e quando colocamos os termos que contém Y em evidência obtemos a expressão Y que multiplica um menos fio 1l - free 2 L2 - cplp igual ao termo de erro essa expressão de forma compacta pode ser definida também por Fi que multiplica lxy T = ET
nesse caso fieli representa o polinômio de grau P em l a escrita compacta do processo é muito utilizada porque ela sempre fica muito anotação do modelo já definimos que cada observação do processo yt uma variável aleatória que afetado por inúmeros eventos ao mesmo tempo então nós temos uma sequência de variáveis aleatórias que juntas formam a trajetória de y supomos que esse processo seja fracamente estacionário então definimos que as funções de densidade de probabilidade dessas variáveis aleatórias apresentam a mesma média e a mesma variância Vamos definir um processo estacionário auto-regressivo de primeira ordem também chamado de
modelo R1 constante por y t = Alpha mais fiz um yt menos um mais é ter a média de Y ou seu valor esperado pode ser escrito por esperança de Y igual a esperança de Alpha mais a esperança de fio um vezes yt menos um nesse caso os coeficientes alfa e filmes são constantes e utilizando as propriedades do valor esperado podemos definir o valor esperado de y um pouco esperança de y t = Alpha mais fio um Esperança dyt menos um pela condição de estacionariedade a gente pode dizer que o valor esperado de yt -
1 = o valor esperado dyp substituindo esse termo isolando do lado esquerdo os termos que contém Esperança dyt chegamos a conclusão que o valor esperado de y = Alpha sobre um menos fiz um Ou seja a média esperada de y depende dos coeficientes alfa e fiz um e eu também que se um processo R1 possui uma raiz unitária ou seja se o coeficiente fiz um da equação foi igual a 1 indicando por exemplo que a Célia não estacionária não é possível obter um valor é esperado de y porque aí a gente teria uma divisão por
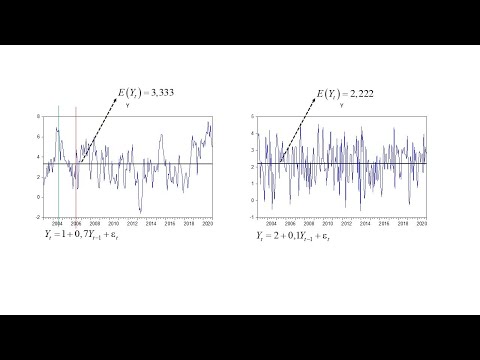
zero e muitas vezes é conveniente também expressar Y como uma variável de desvio da Média essa suposição permite simplificar algumas operações algébricas nesse caso se Y for descrita como desvio da média e sabendo que os modelos em desvio da Média apresenta o intercepto igual a zero a gente pode dizer que o valor esperado de Y também ser igual a zero e vamos ver o que acontece com o valor esperado de y quando os parâmetros do modelo se alteram e na primeira figura eu simulei uma série Y como um processo auto-regressivo = 1 + 0,7 yt
menos um mais o termo de erro o termo de erro é puramente aleatório comédia zero e variância igual a 1 e se aplicarmos a definição do valor esperado de Y com esses parâmetros vamos obter uma média de 3,33 essa média representa a melhor previsão de longo prazo para série Y e vamos ver agora esse outro gráfico foi simulado um processo auto-regressivo = 2 + 0,1 yt menos um mais o termo de erro aplicando a mesma definição anterior o valor esperado de y foi de 2,22 e Perceba como o gráfico da série é diferente No primeiro
caso a série parece se comportar de uma forma - Rua idosa e com padrões mais bem definidos de subidas e descidas por exemplo até 2004 a variável apresenta um comportamento mais autista de crescimento e de 2004/2006 a trajetória da variável apresentam um comportamento decrescente já no segundo gráfico ela se comporta de uma forma bem mais parecida com um ruído branco ou seja parece oscilar sem um padrão definido em torno de um valor constante qualquer isso faz todo sentido porque o coeficiente do parâmetro do componente auto-regressivo foi muito próximo de zero Lembrando que um ruído branco
é uma série estacionária que oscila somente em função de um erro puramente aleatório e os processos autoregressivos de ordens maiores apresentam semelhanças com o modelo R1 por exemplo no caso do cor acesso a R2 temos agora um componente auto-regressivo que representa y dois períodos para trás Subimos novamente que a série são estacionários Ou seja que o valor esperado de y é igual ao valor esperado de yt menos um e dyt menos dois aplicando o operador de esperança matemática e isolando o termo esperança de y ter do lado esquerdo temos que a média esperada de y
= Alpha sobre um menos fiz um menos e 2 e veja aqui o parâmetro do componente yt menos um agora a participa também do cálculo a gente pode generalizar o valor esperado de um processo auto-regressivo estacionário para defasagem p e descrever esse processo como Alfa sobre um menos somatório de fie e com ir variando de 1 até p e vamos ver agora o que ocorre no caso da variância de um processo R1 vamos supor novamente o modelo autoregressivo de primeira ordem dada por y = fio um Y temos um mais o termo de erro a
variância de y pode ser descrita como esperança de y ter menos é dyp elevado ao quadrado veja que o modelo não tem uma constante então implicitamente a gente supõe que Y é uma variável de desvio da Média é matematicamente o valor esperado de uma variável em desvio da média é igual a zero então a variância de yt é reduzida para esperança de y t ao quadrado e vamos substituir Y dentro do parênteses por fim um yt menos um mas é ter e agora vamos resolver o quadrado dessa sono nós temos aqui o primeiro termo ao
quadrado mais o segundo termo ao quadrado mais duas vezes o primeiro vezes o segundo em cada componente ao aplicar o operador de esperança os parâmetros ou as constantes de uma forma geral saindo parênteses vamos primeiro analisar o último termo por preço posição o erro do modelo não possui com relação com a defasagem de y então o valor esperado do produto entre yt menos um e o erro vai ser igual a zero isso elimina o último termo e como yt menos um está em desvio da Média a esperança matemática de yt - 1 ao quadrado é
igual a variância de yt menos um da mesma forma a esperança do resíduo ao quadrado é igual a variância do erro denominamos a variância do erro de Sigma 2 The Air é a definição de estacionariedade a priori nos permite dizer que a variância de yt - 1 = variância dyt então transformando esse elemento e isolando os termos que contém Y do lado esquerdo a gente chega à conclusão que a variância da série temporal do processo R1 pode ser escrita por cima 2D e sobre um menos fiz um ao quadrado e perceba que se o modelo
tiver uma raiz unitária ou seja se o modelo for não-estacionário a gente não consegue chegar ao cálculo da variância por causa da indeterminação que ocorreria no denominador Então para que a variância seja positiva incalculável a condição de estacionalidade requer que o parâmetro fiz seja menor do que 1 e em um modelo a R2 a estrutura da variância muda um pouco vamos supor um processo auto-regressivo de segunda ordem dado por y t = filme yt menos um mais fi2epi estão ter menos dois mais termos de erro agora vamos denominar a variância de Y por Gama 0
Gama 0 é obtida pelo valor esperado de y ao quadrado novamente supomos que Y é um desvio da Média essa expressão também pode ser escrita por Esperança dyt vezes YP agora vamos substituir apenas um Y pelo processo a R2 escrito anteriormente bom então a expressão fica Gama 0 igual a esperança de ypd vezes filme yt menos um mais fi 2yt menos dois mais o termo de erro é o próximo passo é realizar a multiplicação de y contra todos os elementos em parênteses e depois aplicar a esperança matemática em todos esses componentes que foram multiplicados por
propriedade os parâmetros novamente saem da expressão porque são considerados constantes então a variância de yt pode ser descrita como a soma de três termos no primeiro termo temos o parâmetro fiz um vezes a esperança de YP vezes eles não ter menos um a esperança dyt vezes yt menos um é chamada de autocovariância de primeira ordem Nesse contexto a covariância é uma medida de relação entre a variável Y com sua defasagem yt - 1 e essa medida é usada também para calcular correlação entre dois momentos do tempo quando não existe autocovariancia a correlação entre esses dois
termos também é igual a zero e pela estrutura definida do processo auto-regressivo Assumimos que as variáveis possuem alguma relação então a esperança de yt vezes eles vão ter menos um seria por construção diferente de zero aqui vamos chamar essa autocovariancia de Gama 1 é a esperança do segundo componente representa autocovariancia de segunda ordem de y novamente pelo processo a R2 Assumimos que Y não ter e y tem menos dois também possuem alguma relação na prática na equação definimos anteriormente que Y ter depende dos valores de y ter menos dois por isso o termo Esperança dyt
vezes yt menos dois também seria diferente de zero Vamos denominar essa alto covariância de segunda ordem de Gama dois agora temos o último componente para definir a esperança desse produto a gente precisa primeiro Abrir Y ter e definir os kits não ter é igual a filme Eles não têm menos um mas fiz 2yt menos dois mas o termo de erro se a gente introduzisse essa expressão aqui a gente teria uma multiplicação entre todos esses termos e o erro aleatório que já faz parte aqui desse final e aplicando a esperança matemática a gente cancelaria todas as
multiplicações entre o termo de erro e as defasagens de y porque a gente define que os erros são não autocorrelacionados aleatórios Independentes sobraria somente o produto é ter vezes é ter que a multiplicação entre os termos de erro e o valor esperado desse termo é a variância do erro ou seja Sigma do higiene E assim a gente pode escrever a variância do processo a R2 como Gama 0 = fiz um Gama um mais fih2 Gama dois mais Sigma 2D é Resumindo o gama 0 é a variância de y o gama um é autocovariancia de primeira
ordem de y Gama dois é autocovariancia de segunda ordem de y e Sigma 2D é é a variância do erro e generalizando podemos descrever a variância do processo RP como o somatório de fio e Gama aí para ir variando de 1 até p mais Sigma 2D é e no processo R1 a relação entre a condição de estacionariedade o valor do parâmetro auto-regressivo EA variância de y é fácil de ser verificado por exemplo para o processo teve Alliance positiva infinita o parâmetro filme módulo tem que ser menor do que 1 e nesse caso o modelo estacionário
em processos de ordem superior não fica muito claro essa relação mas a gente sabe que para um processo ser estacionário a variância de y numa estrutura R2 R3 ou é Hip também tem que ser positivo infinita Então existe uma série de combinações numéricas aqui que poderiam garantir a propriedade de estacionariedade desses modelos E aí é bom estudar essas características nos ajuda a entender um pouco melhor sobre a estrutura do modelo físico EA relação que elas têm com o processo de estacionariedade da série se identifica por aqui é o próximo e bons estudos [Música]
Похожие видео

9:14
Modelos de médias móveis - propriedades da...
economiaetv
2,023 views

34:22
Introdução aos Modelos Auto regressivos - ...
Outspoken Market
6,121 views

9:53
Using ML To Solve Problems For A Manufactu...
Richard Aragon
975 views

15:52
Aula 15: Conheça a Autocorrelação, uma das...
Análise de Séries Temporais
6,174 views

8:54
Time Series Talk : Autoregressive Model
ritvikmath
330,343 views

5:11
Autoregressive Order one process introduct...
Ben Lambert
178,714 views

29:43
Probability and Statistics: Overview
Steve Brunton
31,230 views

23:10
Séries Temporais - Modelo Autoregressivo A...
Estatística para Concurso
8,423 views

13:16
Time Series Talk : Autocorrelation and Par...
ritvikmath
412,375 views

6:15
O que é estacionariedade?
economiaetv
5,416 views
5:01
What are Autoregressive (AR) Models
Aric LaBarr
124,865 views

13:36
Aula 30: Modelo de Média Móvel: Definição ...
Análise de Séries Temporais
1,270 views

16:44
Aula 24: Saiba o que é o Modelo Autoregres...
Análise de Séries Temporais
4,642 views

9:26
Time Series Talk : ARIMA Model
ritvikmath
331,181 views
11:20
The Expected Value and Variance of Discret...
jbstatistics
360,665 views

14:27
Análise de estacionariedade (gráficos e te...
economiaetv
8,796 views

12:13
Propriedade de invertibilidade dos modelos...
economiaetv
1,357 views
![ARDL - Modelos Autorregressivos e de Defasagens Distribuídas [TEORIA]](https://img.youtube.com/vi/eK0sHKLxHO0/mqdefault.jpg)
9:13
ARDL - Modelos Autorregressivos e de Defas...
economiaetv
173 views