Redes Neurais: Exemplo de propagação de entradas no MultiLayer Perceptron (MLP)
1.74k views1810 WordsCopy TextShare
Fernando dos Santos
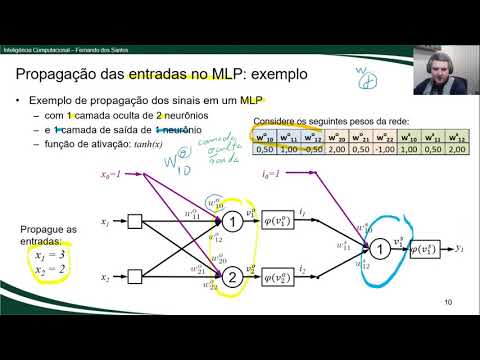
Neste exemplo temos uma rede neural com:
1 camada de entrada com 2 neurônios sensoriais;
1 camada oc...
Video Transcript:
é o que eu vou mostrar para vocês primeiramente é como ocorre a propagação das entradas no multilayer perceptron E aí eu vou fazer esse exemplo aqui com vocês ou para pagar uma única vez uma única entrada só precisa dois valores aqui de entrada Nós Vamos considerar esse exemplo aqui ou de um multilayer perceptron ou seja ele tem uma camada uma camada oculta com dois neurônios que essa camada camada oculta aqui essa camada oculta e ele tem uma camada de saída uma camada de saída com um neurônio que essa camada de saída aqui certo é eu já tô dando aqui para vocês alguns valores de peso certo ó cada um desses dessas entradas aqui tem o seu respectivo o peso que nós vamos usar para fazer a propagação Eu já coloquei aqui ó os valores por exemplo aos valores aqui agora que eu lembrei que tem uma uma diferença de notação aqui não sei se vocês perceberam mas antes enquanto lá no percebe Tron simples a gente tinha só o w com um esse um esse aqui embaixo por exemplo esse J agora Como nós temos várias camadas a picada camada pode ter vários neurônios bom e cada neurônio pode ter várias entradas especificação aqui a formalização dessa rede neural específica mais índices aqui por esses pesos como é que você vai interpretar esses vídeos Vou colocar aqui todo neurônio então por exemplo Vamos pegar esse aqui esse cara aqui é o w 110 e ele tem um esse aqui em cima que parece 10 mas é uma letrinha ok O que que significa esses valores aqui essa letra que aparece aqui em cima é a camada se ela é uma camada oculta ou se ele é uma camada SD saída Essa é a policial aqui da camada por exemplo ó e oculta o Ultra oculta oculta o culto só para a gente não se perder Já o neurônio lá na camada de saída ela tem um curso super escrita QSS para indicar que é um neurônio da camada isso aí e sem relevante lá para o treinamento depois então aqui já tem os dois slides bom né esse primeiro slide aqui é só para porque vocês relembrarem o esquema de propagação né as formas pra gente calcular e aqui tal enunciado da do exercício que eu tô pedindo a propagação e agora vamos fazer aqui a propagação juntos então então nessa rede eu tenho eu tenho duas camadas uma três na verdade não é uma camada de entrada uma oculta e uma saída para eu calcular a saída definitiva que é o que interessa eu tenho que passar essas entradas aqui sequência para frente por essa rede para gente ver o que que vai acontecer então vou fazer aqui com cores para a gente identificar bom aqui estão as entradas preço e dois então o valor do x 1 vai vale três Nessa entrada e o do x 2 vai valer 21 eu vou para pagar essas entradas Por toda a minha rede para calcular saídas tem que fazer em sequência vou fazer primeiro vou usar cores aqui primeiro eu vou fazer preci neurônio aqui é um neurônio em vermelho a gente calcular essa saída aqui E esse valor de saída intermediária aqui para isso eu vou usar os pesos né estão aqui ó os pesos desse primeiro neurônio são esses pesos que eu destaquei aqui em azul certo então vamos lá para calcular esse ver vamos calcular o ver que vou fazer Deixa eu tirar esse vou fazer aqui do lado preocupar para dar espaço para gente ir fazer de todos eles botar um pouquinho mais para cima e aqui um beijo conseguir fazer então o valor de saída ver do neurônio da camada oculta neurônio um da camada oculta vai ser o seu matorio dos pesos vezes os valores de entrada então eu vou ter tenho três pesos e três entradas vai ser w o em 10 vezes x 0 mais W1 xx1 mais wa12 x 1 x 2 são as entradas pesos esses pesos aqui pé vezes aquelas entradas ali bom agora é só substituir né olhar aqui na nossa nossa tabela ww10 tá valendo 0. 5 XX x0 x0 sempre fixo em um vezes um mais W1 aqui um tá valendo um vezes x 1 x 1 tá aqui três mais w12 daqui está valendo ou menos 0. 5 xx2 que tá aqui dois então vamos lá aqui eu vou ter 0.
5 + 3 + - 1 é isso aqui vai me dar e aqui então vou ter 3 e Meio - 1 2,5 Tá certo então esse valor veio aqui é 2,5 Preto calcular a saída a definitiva deste neurônio sendo intermediário eu tenho que aplicar a função de ativação sobre aquele valor ali qual que é essa função de ativação função e ativação tangente hiperbólica sanduíches Então vai ser TAM HD 2. 5 isso aqui eu vou usar o vou ver eu vou usar que eu vou ver para calcularmos 12. 5 e daí eu voltei aqui que o valor da tangente hiperbólica aumentar um pouco uso a quem gente hiperbólica do valor 2.
5 é 0. 98 posso arredondar para 0. 99 usar o ponto zero 98 o arredondado p099 então voltando aqui o valor é 0.
99 esse é o valor da saída fizer aqui ó 099 do neurônio um é igual a zero. Nove nós nós fizemos o primeiro passo para esse neurônio um da camada oculta agora tem que fazer por segundo para usar Azul aquela agora tem que fazer para esse neurônio fazer a mesma propagação usando esses valores de peso aqui o e propagando as mesmas mesmos sinais de entrada então vamos lá bom então aqui por ver da camada oculta do neurônio dois vai ser igual de novo né w o neurônio dois entrada zero vezes x 0 mais w o neurônio dois entrada 1 vezes x 1 + w o é camada oculta neurônio dois entrada 2x x 2 substituindo peso w o camada é e neurônio dois valor 2 vezes valor de entrada que é fixo em um mais wh21 Oi tá aqui 0. 5 às vezes x 1 que é 3 mais o w o 22 tá aqui que é menos um às vezes x 2 que é dois os dois mais 1.
5 ma - menos dois então aqui eu vou ter 1. 5 de novo né esse 1. 5 é esse valor ver para saber o valor i.
a. do neurônio dois tem que passar a função de ativação sobre o V2 a camada oculta ó e vai ser igual TAM HD 1. 5 é igual e eu tenho anotado aqui vou usar a minha minha cola para não precisar abrir o Wolfram mas isso aqui vai dar 0.
91 então esse 0. 91 esse valor do idoso com isso nós finalizamos a propagação pressa primeira camada e oculta aqui usando esses pesos ali o que falta fazer agora é calcular o valor de saída para o último neurônio E aí a gente conseguir calcular a saída definitiva da rede e deixar pois aqui pro lado e pronto para fazer isso aqui então vou usar esses pesos aqui e vamos agora calcular a saída ver a ver camada de saída neurônio um vai ser igual de novo né tem que pegar esses valores de peso aqui no ficar pelas entradas então vou ter w camada de saída neurônio um entrada zero vezes esse cara aqui ó que é o fizeram entrada Extra né aqui no caso dos neurônios da camada de saída não é mais x aí agora em casa né porque ela corresponde a saída intermediária da camada anterior vezes fizeram mais W camada de saída um vezes i G1 é mais W camada de saída 12 x e 21 e agora é só substituir novamente né tem aqui o peso um w0 é um vezes e zero é sempre fixo em um mais W1 da camada de saída tá aqui zero. Cinco vezes e um o que que é esse youm esse e um essa entrada que vem aqui no neurônio que corresponde a saída daquele neurônio anterior kewe um Qual que é o valor de um que nós temos calculado antes tá aqui ó e 10 99 então a entrada desse neurônio aqui que corresponde a saída do neurônio um da camada anterior 0.
99 mas w12 que tá valendo 2 vezes Windows esses dois é esse cara que quer a saída do neurônios da camada anterior calculamos ac091 e pronto fazendo isso aqui aqui vai dar um aqui vai dar 0. 49 alguma coisa assim né mas é duas vezes 91 da 1. 8 alguma coisa eu tenho aqui na minha na minha cola que esse valor aqui vai dar aproximadamente de chover aqui 3.
3 esse 3. 3 esse valor ver aqui para calcular a saída definitiva tenho que passar pela função de ativação Y um vai ser igual a função de ativação sobre o valor ver e da camada de saída neurônio função de ativação sobre o valor 3. 3 que a tangente hiperbólica né hum HD 3.
3 guardá-la segundo as minhas anotações aqui o valor 1.
Related Videos

7:54
Redes Neurais: Como determinar a arquitetu...
Fernando dos Santos
1,217 views

15:07
Avaliação de Modelos Preditivos: Validação...
Fernando dos Santos
1,316 views
2:49:19
Algoritmo da retropropagação de erros (Bac...
Centro de Excelência em IA & Deep Learning Brasil
24,583 views
16:38
Modelo Conceitual, vídeo 6
profantini
9 views

27:57
Multiplexers
José Sousa
18 views

17:52
Teoria sobre Redes Neurais Artificiais: cá...
IA Expert Academy
14,637 views

25:14
(ML) Redes neuronales ‐ Introducción
El Umbral
56 views

42:54
Redes neurais e multilayer perceptron - Au...
Diogo Cortiz
17,245 views

7:20
Redes Neurais: Introdução ao MultiLayer Pe...
Fernando dos Santos
934 views
23:38
Buscas em Espaço de Estados: Resolução do ...
Fernando dos Santos
1,019 views
1:40:06
Análise Estrutural - Método dos Esforços
Douglas Andrin Edmundo
19 views

7:48
Teoria sobre Redes Neurais Artificiais: De...
IA Expert Academy
3,528 views

20:08
HIBRIDAÇÃO E CLASSIFICAÇÃO DOS CARBONOS
Revisões Gerais
8 views
23:08
Inteligência Artificial - Aula 04 - Exempl...
Samuel Felipe Moreira
10,478 views

10:56
Redes neurais artificiais #17: Descida do ...
Machine Learning para humanos
1,501 views

24:46
Formulação do Problema dos Jarros para Apl...
Fernando dos Santos
399 views
32:22
Principais Exercícios de TIPAGEM SANGUÍNEA...
Pedro Henrique Reis
29 views

20:10
ELETRODINÂMICA ASSOCIAÇÃO DE RESISTORES
LAELSON PEREIRA SANTOS
36 views
5:38
Resolução de Exercício: Buscas Competitiva...
Fernando dos Santos
2,645 views

8:10
PRIM
CDanna
8 views