Markov Chains Clearly Explained! Part - 1

hello people from the future welcome to normalized nerd today i'm gonna talk about markov chains this is a concept that is used in many places from statistics to biology from economics to physics and of course in machine learning i guess some of you have heard of markov chains before but don't have a clear idea about it i hope by the end of this video you will have a fair understanding of markov chains and you will know why they are so interesting if you are new here then please subscribe to my channel and hit the bell

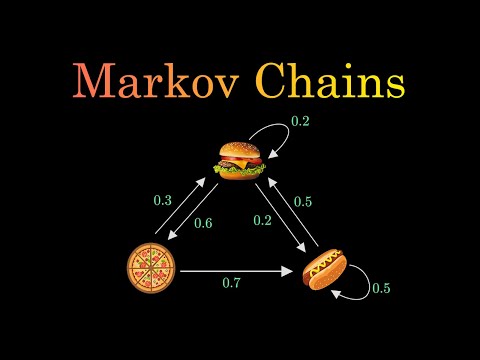
icon i make videos about machine learning and data science regularly so let's get started well as you know me i like to start with an example assume there's a restaurant that serves only three types of foods hamburger pizza and hot dog but they follow a weird rule on any given day they serve only one of these three items and it depends on what they had served yesterday in other words there is a way to predict what they will serve tomorrow if you know what they are serving today for example there is a 60 chance that

tomorrow will be a pizza day given that today is a hamburger day i'm gonna represent it in the diagram as weighted arrows the arrow originates from the current state and points to the future state i'm using the term state because that's the convention let's see another one there's a 20 chance that tomorrow again they will serve hamburgers and that is represented as a self-pointing arrow well each arrow is called a transition from one state to the other now i'm gonna show you all the possible transitions the diagram you are seeing right now is actually a

markov chain yes the concept is that simple now let's discuss some properties of the markov chain the most important property of the markov chain is that the future state depends only on the current state not the steps before mathematically we can say the probability that n plus 1 x step will be x depends only on the nth step not the complete sequence of steps that came before n at first glance this might not seem so impressive but on a closer look we can see that this property makes our life a lot easier while we tackle

some complicated real world problems let's understand it a little better suppose the restaurant served pizza on the first day hamburger on the second and again pizza on the third day now what is the probability that they will serve hot dogs on the fourth day well we just need to look at the third day and it turns out to be 0.7 this is the heart of markov chains and it's known as the markov property the second important property is that the sum of the weights of the outgoing arrows from any state is equal to 1. this

has to be true because they represent probabilities and for probabilities to make sense they must add up to one here i should probably tell you that there are certain markov chains with special properties but they deserve individual videos on their own so here i'm just gonna stick to the basic kind of markov chains now that you know what a markov chain actually is let's explore our markov chain by doing a random walk along the chain initially we are on a hamburger day let's see what they serve for 10 consecutive days so after 10 steps we

have a situation like this now we want to find what is the probability corresponding to each of the food items aka the probability distribution of the states well it's pretty simple just divide the number of occurrences of an item by the total number of days for hamburger it's 4 upon 10 for pizza it's 2 upon 10 and it's 4 upon 10 for hot dogs it's obvious that if we change the number of steps then these probabilities will vary but we are interested in what happens in the long run do these probabilities converge to fixed values

or they continue to change forever i wrote a python script to simulate the random work for hundred thousand steps i found that the probabilities converge to these values and this probability distribution has a special name which is the stationary distribution or the equilibrium state this simply means that this probability distribution doesn't change with time for this markov chain okay so we have managed to find the stationary state but this method doesn't seem to be very efficient is it moreover we don't know if there exists any other stationary states well a better way to approach this

problem is linear algebra let me show you first of all let us think about how we can represent this markov chain more efficiently well this is essentially a directed graph so we can represent it by an adjacency matrix if you don't know what it is then please don't worry it's very simple the elements in the matrix just denote the weight of the edge connecting the two corresponding vertices for example the element in the second row and first column denotes the weight or the transition probability from pizza to hamburger if an element is 0 then it

just means that there's no edge between the two vertices this matrix is also called transition matrix let's denote it by a remember that our goal is to find the probabilities of each state conventionally we take a row vector called pi whose elements represent the probabilities of the states basically pi denotes the probability distribution of the states suppose in the beginning we are on a pizza day so the second element which corresponds to the pizza becomes one and other two remain zero now see what happens when we multiply this row vector with our transition matrix we

get the second row of the matrix in other words we get the future probabilities corresponding to the pisa state then we take this result and put it in the place of pi zero we will do this once again now if there exists a stationary state then after a certain point the output row vector should be exactly same as the input vector let's denote this special row vector as pi so we should be able to write pi a equals pi if you have ever taken a course of linear algebra then you should find this equation somewhat

similar to a very famous equation yes i'm talking about the eigenvector equation consider lambda equal to 1 and just reverse the order of multiplication and you have got our equilibrium state equation how to interpret this you might ask well we can imagine that pi is a left eigenvector of matrix a with eigenvalue equal to 1. please pause the video if you need a moment to convince yourself now the eigenvector must satisfy another condition the elements of pi must add up to 1 because it denotes a probability distribution so after solving these two equations we get

the stationary state as this it tells us that the restaurant will serve hamburger about 35 of the days pigs are about 21 and hot dog about 46 percent using this technique we can actually see if there are more than one stationary states can you guess how we just need to see if there exists more than one eigenvectors with eigenvalue equal to 1. isn't it super elegant now let's compare this result with the previous one that we got from our simulation look how close they are they kind of validate each other by now you should have

a very good understanding of markov chains and you should be able to identify markov chains successfully obviously there is much more to learn about different kinds of markov chains and their properties that cannot be covered in a single video if you want me to make more videos on this topic then please let me know in the comment section if you like this video do share it and please please please subscribe to my channel stay safe and thanks for watching [Music] you