Retas paralelas cortadas por uma transversal

o ângulos formados por duas retas paralelas e uma transversal olha essa figura que eu vou desenhar aqui ó uma circunferência em 360 graus na verdade então vamos fazer assim vamos traçar uma reta dividindo essa circunferência ao meio e agora cada uma dessas metades tem exatamente 180 graus concorda vamos acrescentar mais uma reta e se chamar esse ângulo aqui de ar e esse outro aqui bebê agora nós podemos afirmar com toda a segurança que a medida do ângulo a mas a medida do ângulo b = 180 graus serra quando isso acontece esses dois ângulos são suplementares

ó fica a dica ângulos formados por semi-retas opostas são suplementares vamos continuar dando nome aos ângulos aqui é ser e esse ângulo aqui eu vou chamar de da mesma forma podemos afirmar que ser mais de demais de ah mas se são iguais a 180 graus tô tomando como centro da circunferência que tem um vértice em cada ângulo podemos afirmar que os ângulos a = di e b = c são opostos pelo vértice agora imagine se eu copiar jr e desenhá-la um pouco abaixo os ângulos formados por essa cópia dr que agora eu vou chamar de

reta s formaram ângulos congruentes a b c e d só que agora eu irei chamar d f g h de imediato vem na minha mente a seguinte associação a = f b = c = h e d = i isso é tem as mesmas medidas ainda referente a reta s é possível também afirmar que a mais h demais ir ser mais f e demais são iguais a 180 graus agora vem comigo presta bem atenção no que eu vou é porque é muito importante essa parte entre as retas r s pintado de azul vamos chamar de

região interna e acima da reta r e abaixo na reta s pintada de verde chamaremos de região externa agora observe os ângulos cf e veja que ambos se encontram do mesmo lado da reta t então vamos dizer que esses ângulos são colaterais internos a palavra colateral significa do mesmo lado o mesmo acontece com os ângulos de g só que agora do lado direito da reta t com esse mesmo pensamento podemos dizer que os ângulos anhangá bee também são colaterais só que externos por isso também são suplementares agora que acontece eu pegar dois ângulos da região

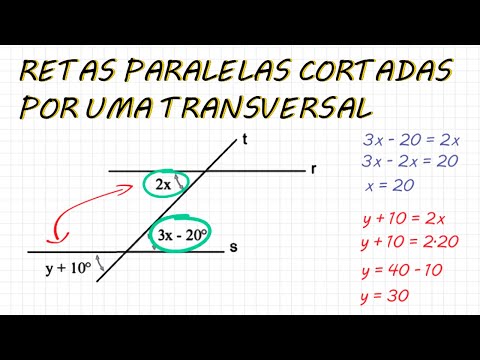
interna mas alternando os lados como por exemplo ceg1 e a resposta é alternos internos e tem a mesma medida isso se aplica também a usar o ternos e externos aí e bh eles também possuem a mesma medida vamos resolver algumas questões para a gente poder fixar o que a gente aprendeu e calcule o valor de x e y na figura abaixo sendo r s e t retas paralelas observando a figura nós podemos perceber e esses ângulos 2x e 3x menos 20 são ângulos alternos internos e como nós aprendemos ângulos alternos internos são congruentes então posso

escrever assim ó 3 x - 20 = 2x resolvendo essa equação vai ficar essa fórmula 3 x passo 2 x para o primeiro membro ele vai vir subtraindo então fica 3 x - 2x = 20 logo valor de x = 20 para achar o valor de y eu vou pegar por exemplo o ângulo y mais 10 e o ângulo 2x esses dois ângulos são correspondente e os ângulos correspondentes também são congruentes aí a equação fica assim ó y + 10 = 2x e agora eu sei que x = 20 então fica y + 10 =

duas vezes 20 então y = 40 - 10 y = 30 beleza vamos resolver a próxima e determine o valor de x na figura nesse tipo de figura você repara que os ficar aqui sozinho a gente não tem uma referência né para dizer se ele alterno interno colateral de não tem diferença nenhuma então vamos fazer o seguinte nós vamos traçar aqui uma reta passando pelo vértice desse ângulo x agora nós podemos perceber claramente que aqui também é 146° porque esses dois ângulos são alternos internos e os ângulos alternos internos têm a mesma medida da mesma

forma nós podemos dizer que aqui embaixo é 154 pelo mesmo motivo são ângulos alternos internos agora nós podemos dizer o seguinte olha uma circunferência não tem 360 graus se aquilo tem 146 aquele tem 154 e aqui eu tenho x significa e se eu somar tudo isso vai ter que dar 306 bom então vai ficar assim ó 154 mais 146 + x = 360° 154 mais 146 = 13 anos então fica assim 300 + x = 360 a x = 360 passado 300 por outro lado ele vai ficar negativo né assim a gente encontra o valor

de x de 60° beleza vamos resolver mais uma e na figura os pontos a e b estão no mesmo plano que contém as retas paralelas rs assinale o valor de ar essa questão é um pouco parecida com a anterior né então vamos traçar duas retas paralelas à rs passando pelo vértice b e pelo vértice a agora a gente pode perceber que aqui é 30 graus porque é correspondente com aquele agora em cima e também é 30 graus e se o total era 40 aqui embaixo só pode ser 10 na verdade agora aqui embaixo olha essa

parte aqui tem que ser 60° porque e alterno interno e os ângulos alternos internos eles são congruentes ou seja ele tem a mesma medida se aqui é 60 eu já achei o valor dessa outra parte aqui que é 10° o meu alpha ele vai ter exatamente 70 graus a resposta ele atende então é isso aí pessoal espero que vocês o vídeo tem o compreendido desfila que bacana e se inscreva no canal ative também as notificações para você poder receber conteúdos iguais a isso tá bom então essa grande abraço tchau tchau