Entenda agora o que é a equação da linha elástica em vigas
10.16k views2405 WordsCopy TextShare

Prof. Carol Grossi
Olá pessoal! Nesse vídeo eu vou te ensinar como encontrar a equação que define a posição da linha el...
Video Transcript:
e aprenda de uma vez por todas o conceito da linha elástica Olá no vídeo de hoje eu vou te ensinar o conceito da linha elástica eu te garanto que entendendo o conceito vai ser muito mais fácil para depois você interpretar seus resultados para gente encontrar a equação da linha elástica existem diversas maneiras por integração do momento fletor por integração da carga distribuída por superposição dos efeitos pelo método dos momentos diárias e por funções de singularidade hoje a gente vai iniciar o estudo da linha elástica aplicando o método de Integração no momento fletor antes de começar
a aula não esqueça de deixar o seu like para ajudar o canal e se inscrever para não perder nenhum vídeo toda terça-feira nós temos vídeos não para o vídeo dessa semana a gente ainda vai ter um bom esse vídeo vai ser para vocês entenderem de uma vez por todas o conceito e no próximo vídeo postado ainda hoje também a gente vai fazer um exercício para a gente aplicar o que a gente aprendeu nessa matéria gente é e vocês façam exercícios tá você tem que treinar a o método porque senão treinar fica muito difícil da gente
conseguir ganhar é esse que a gente não treinar fica muito difícil da gente ganhar habilidade para interpretar todos os diferentes problemas que envolvem a equação da linha elástica quando a gente conversou sobre flexão nesse vídeo aqui eu expliquei para vocês que uma via submetida um momento fletor positivo ela tem as suas fibras de cima comprimidos e as fibras de baixo tracionada pelo menos como acontece com essa régua aqui chegamos a conclusão que em algum lugar ele não vai existir nem compressão nem para-sol Esse lugar é o eixo que passa pelo centróide de todas as seções
transversais e a gente chama ele de eixo neutro se a nossa vida primeiramente estava reta e ao aplicar o momento setor ela se desloca para baixo Existe uma forma de calcular o deslocamento desse eixo neutro em qualquer. e ao longo do comprimento da vida para isso a gente vai precisar encontrar a função que descreve essa curva Então pensa comigo na hora que a minha vida reta ela sofre flexão ela passa a ser uma curva e eu posso definir essa curva matematicamente em função da posição X então o que a gente vai achar que é uma
função y DX Vamos pensar lá no matemática quando escreva a função y e x é igual a x ao quadrado mais 2x mais um Eu estou desenhando essa parabolt se eu quero saber por exemplo o valor de y para x = 1 é só substituir um na equação correto substituindo na equação a gente encontra Quanto que vale Y para x = 1 eu também posso encontrar esse valor caso e e nessa curva em escala E aí eu encontro esse valor pra ficar meio isso é exatamente a mesma coisa que acontece no nosso problema de linha
lá eu vou encontrar uma função ydx que vai me dizer o valor do deslocamento vertical do eixo neutro em qualquer posição de x ou seja em qualquer ponto ao longo do comprimento da vida essa função ela pode ser representada em um gráfico ou então o enterro de engenharia a gente chama de diagrama de deflexão do eixo neutro que é a nossa linha eu acho obviamente aqui para os nossos problemas esse gráfico a gente não desenha ele em escala ele é só uma ideia de como que vai ficar a posição final na nossa vida quando ela
está submetida a carregamentos transversais que gera um momento fletor lá dentro então existe uma relação muito importante entre a curvatura da linha elástica e o o corretor associado é importante lembrar que que eu estou simplificando o problema falando que todo deslocamento transversal que acontecer nessa vida ele é único e exclusivo gerado pelo momento fletor Essa aproximação é uma aproximação legal porque na maioria das nossas vidas que regem o comportamento é realmente o momento fletor Então vamos ver essa relação se eu vou ter ao fundo o gênio e se comportar de maneira linear elástica é válida
essa equação que disse para gente que um sobre whole é igual a m sobre aí como entendeu que cada um desses símbolos representa aqui para gente um sobre ro é a curvatura deformada da vida ou seja a curvatura da linha elástica essa linha em azul mostrado aí no desenho para vocês é uma representação da linha elástica se a gente pensar a curva como um arco de circunferência a gente pode desenhar o seguinte não existe um centro o e um raio então a curvatura nada mais é do que o inverso desse raio m é o momento
fletor e aqui vai ser muito importante a gente encontra a equação que descreve o momento fletor ao longo na vida tá isso vocês viram lá em estática quando você sabe um aprendendo a traçar diagramas nós vamos ter vídeos aqui no canal também sobre esse tema então aqui para o nosso caso a gente sempre vai ter que procurar um M que seja em função de x é é o módulo de elasticidade e do material que compõe amiga um é a inércia e da seção transversal em torno na linha neuro é importante a gente também define as
coordenadas que a gente vai usar no problema o eixo X é esse eixo em amarelo definido ao longo da vigas e positivo da direita para a esquerda igual ao mostrado aqui o eixo Y e a positivo a partir do eixo neutro para cima dependendo da bibliografia que vocês estão utilizando vocês vão achar ydx oi ou então ver disse a curva Daniel acho que ela expressa matematicamente por essa equação aqui vender um sobrevoo igual a derivada segunda de y em relação a x sobre um mais dydx ao quadrado elevado a 3 meses hifas Agora complicou fera
fera fera fera fera não sai do vídeo a gente vai simplificar as coisas você é mais forte do que uma equação feia da matemática Vem comigo a gente já tinha visto que um sobre ro era igual a m sobre em Então vamos substituir esse resultado nessa nova equação se ac = M sobre ei e essa equação representa uma equação diferencial não linear de segunda ordem e sua solução da forma exata da linha considerando é claro que as informações dentro da vida são causadas somente por flexão mas pra facilitar nossa vida a gente vai simplificar essa
equação é e na grande maioria dos problemas na engenharia a gente sempre vai estar no campo de pequenas deformações e pequenos deslocamentos as próprias normas vão alimentar esses valores de deformação e deslocamento a valores bem pequenas bom como consequência a gente tem um termo dessa equação que a gente vai poder ver qual que é esse termo dydx vai ser para a gente a inclinação da linha neutra é mais ou menos assim se eu tenho uma curva que é função de x y e x e aderivo essa função em relação a x no ponto por exemplo
esse contém amarelo eu encontro a inclinação desse ponto ou seja o nosso pega essa inclinação ela está representa E aqui nessa equação dydx essa inclinação Ela é pequena porque a gente está falando de pequenas deformações e pequenos deslocamentos quando eu levo ela o quadrado ela fica muito pequena em relação a unidade eu poderia dizer que eu tenho um mais 0,00001 por exemplo algo que quando eu somar é desprezível então para facilitar nossa vida a gente considera que esse termo é 01 elevado a 3 meios é um e como diversificar Então a nossa equação para encontrar
a linha elástica a derivada segunda de y em relação a x vai ser igual a e me lembrando que esse M também é função de x sobre hein a equação a gente consegue resolver obviamente a gente não tem mais a solução exata do problema mas temos uma solução muito próxima do valor real e aqui no engenharia a gente sempre trabalha com isso gente é sempre custo-benefício então eu abro mão de saber o valor exato da posição da minha linha elástica para eu facilitar os meus cálculos sabendo que eu estou dentro de uma margem de segurança
Ok essa aproximação não vai influenciar em nada negativamente nos resultados a fessora Agora sim o a derivada segunda de 1 m DX e facilitou a nossa vida né agora tá tudo maravilhoso Só que não né Calma calma vai dar certo vem comer o que significa procurando eu estou procurando Y DX ele tá aqui ó Ipê bom então a gente vai ter que integrar duas vezes os dois lados dessa equação para que a gente encontre o ydx que ela função que vai me dar a posição da linha elástica Ou seja a posição transversal de qualquer ponto
do eixo neutro da Viga aqui esse trabalho vai ser mais simples porque a gente sempre vai estar lidando com polinômios tão a integral de polinômio é uma entregar entregar a integral de polinômios é uma integral mais simples vamos ver como que isso vai ficar a integral Oi Dede ao quadrado Y sobre de x ao quadrado tem que ser igual a integral dmdx sobre e em quando o íntegro lado de cá eu retiro 1° da derivada então vai ficar dydx sobre de x é igual eu vou precisar integral meu momento fletor tá mdx Way ele é
constante então ele se mantém o mesmo e eu tenho que adicionar uma constante de integração essa equação ela representa a inclinação da linha elástica em qualquer ponto lembra que dá Y B X = festa então a gente pode né Igual a isso afeta DX continuando eu preciso integrar mais uma vez Então vamos lá a integral de dydx de X = integral e quando a gente integral lado de cá a gente diminuiu 1° da derivada chegaremos em ydx vai ser igual a gente vai ter que integral momento e mais se um X + C2 tão vejam
né apareceu mais uma constante de integração E aí o mais profundo espera aí Que diabos é esse C1 e C2 essas valores são constantes de integração Se eu quisesse integrar essa função y de x é igual a x ao quadrado sobre dois o que que eu teria um X ao cubo sobre 3 + 2x ao quadrado sobre dois correto é errado porque imagina o contrário agora eu vou derivar a seguinte expressão sem o derivar-se expressão em relação a x qual que vai ser o meu resultado 3X ao quadrado sobre 3 + 4 x sobre 2
é igual então a x ao quadrado mais 2x tudo bem agora vou derivar é essa outra expressão o que que eu vou ter como resposta 3X ao quadrado sobre 3 + 4 x sobre 2 = x ao quadrado + 2x percebam que tem um termo constante nessas duas expressões que quando eu derivo em relação a x ele some mas essa expressão é diferente dessa essa expressão de cima vai me dar uma função é diferente do que a expressão de baixo então a gente precisa colocar essas constantes de integração quando a gente faz a integração porque
tem só um valor para cada constante que vai me dar exatamente o problema é que eu tô procurando bom então agora voltando aqui no nosso problema como que eu vou encontrar os valores corretos de C1 e descer dois a gente encontra esses valores a partir das condições de contorno do nosso problema o que que são essas condições de contorno são as vinculações que eu aplico a minha filha então por exemplo se eu tiver uma viga bi-apoiada o que que eu voltei como condição de contorno nesse problema nos apoios eu sei que eu não tenho deslocamento
transversal o apoio de primeiro e segundo gênero ele serve justamente para falar que naquele. Eu não tenho um deslocamento E aí nesse caso se eu fizesse x igual a zero eu tenho que Obrigatoriamente ter que Y também é igual a zero por que que eu tenho um apoio do segundo gênero que impede o deslocamento transversal a mesma coisa lá no final da vida eu tenho um apoio de primeiro gênero que vai me garantir que para x = l o meu Y também seja igual a zero o último tipo de vinculação que a gente pode ter
é um engate e o que que o engaste garante para gente por exemplo nessa posição onde ela é o tamanho da virilha para x igual a zero eu também voltei Y = 0 porque amanhã o engaste impede esse deslocamento transversal 1 e para x igual a zero eu também vou ter que dydx é igual a zero porque eu acho que é o nosso apoio terceiro gênero ele impede além do deslocamento transversal a rotação onde ele está aplicado sabendo o tipo de vinculação que o seu problema tem você vai conseguir encontrar as constantes C1 e C2
e consequentemente você você vai ter a expressão que define a inclinação da linha elástica em qualquer ponto e o deslocamento transversal em qualquer. Pessoal de novo ressaltando é muito importante que vocês trem os exercícios dessa matéria você tem que fazer os exercícios para vocês conseguirem desenvolver com maior facilidade tanto as equações de movimento quanto as integrações e as aplicações das condições de contorno a linha elástica é um conteúdo muito e principalmente para aqueles que querem continuar na área de estruturas utilizando os conceitos da linha elástica a gente pode fazer verificações muito rápidas de deslocamentos máximo
100 vigas que a gente chama de flecha e adquirir um pensamento crítico de acordo com os valores que o software que você está usando vai te dar então nessa semana a gente vai ter um bônus dois vídeos no canal frase no café para mim os exercícios são esses vídeos e compartilhem com seus amigos eu não quero ver mais ninguém eu não quero ver mais ninguém ela Ei só Cebolinha pelando eu não quero ver mais ninguém errando a linha elástico aqui no próximo vídeo eu vou desenvolver um exercício de linha elástica com vocês Te vejo no
próximo vídeo Um abraço e
Related Videos

18:57
Linha elástica: viga biapoiada e carregame...
Prof. Carol Grossi
5,520 views

14:37
12.3 Deflexão em Vigas e Eixos - Linha El...
EAexatas
25,112 views

25:14
EXERCÍCIO RESOLVIDO: viga engastada e carg...
Prof. Carol Grossi
8,504 views

14:39
Aprenda agora o que é tensão na resistênci...
Prof. Carol Grossi
13,136 views
16:17
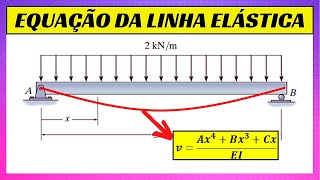
How to Determine the FUNCTION OF THE BEAM ...
Steven Róger
12,077 views
50:06
Deflexão de vigas e eixos (Integração direta)
Prof. João Paulo - Ifes São Mateus
2,786 views
24:48
Equação da Linha Elástica (viga hiperestát...
Prof. Arlindo Pires Lopes, Ph.D.
2,433 views

11:12
Exercício resolvido linha elástica: Beer, ...
Prof. Carol Grossi
4,269 views

22:02
Vigas Linha Elástica - Teoria e Exemplo | ...
Tutorial Mecânica
3,557 views

29:45
12.4 Deflexão em Vigas e Eixos - Linha Elá...
EAexatas
11,978 views

37:04
Flambagem de Colunas - Teoria e Exemplo | ...
Tutorial Mecânica
16,435 views

15:58
Entenda o Conceito da Flexão pura SEM comp...
Prof. Carol Grossi
5,403 views

15:23
Equação da linha elastica
Banca Virtual BV
37,800 views

23:28
Calcule as REAÇÕES DE APOIO em VIGA: guia ...
Prof. Carol Grossi
11,561 views

10:15
Determination of the Elastic Line Equation...
Steven Róger
7,688 views
25:56
Deflexão de vigas e eixos (Método da Super...
Prof. João Paulo - Ifes São Mateus
11,754 views
26:17
Linha Elástica - Exercício 01
Murilo Silva
13,661 views

21:07
Resistência dos Materiais - Aula 11 - Defl...
UNIVESP
42,524 views

22:56
Exercício 01: Deslocamentos na flexão - vi...
Mauricio Carvalho
6,283 views