Análise da Tendência Determinística (Séries Temporais)
7.16k views1461 WordsCopy TextShare
economiaetv
➡️ CONSULTORIA, ASSESSORIA ACADÊMICA E PARCERIAS: economiaetv@gmail.com.
➡️ CURSO: INTRODUÇÃO A MOD...
Video Transcript:
Oi Oi pessoal tudo bem com vocês no vídeo de hoje nós vamos estudar sobre componentes não observadas de uma série temporal especificamente a gente vai abordar o componente da tendência é uma série temporal pode ser decomposta em quatro elementos a tendência é sazonalidade o ciclo e um termo puramente estocástico cada elemento desses representa um padrão de comportamento previsível que uma determinada variável possui ao longo do tempo Nós estudamos esses componentes por dois motivos principalmente o primeiro deles é para controlar influência que eles têm sobre a dinâmica de uma série temporal sem esse controle o pesquisador
pode enfrentar problemas de viés e de inconsistência na modelagem e o segundo é para analisar a própria influência desses componentes da dinâmica da série quanto melhor é o entendimento dessa dinâmica melhor será a previsão do modelo nós vamos iniciar com um componente de tendência a maioria das séries econômicas varia com o tempo por exemplo a produção o emprego inflação Nesse contexto a tendência pode ser entendida como um movimento sistemático lento e de longo prazo no nível médio da série esse componente Mostra o caminho natural e determinada variável percorre ao longo do tempo na economia a
tendência é definida principalmente pelas preferências da sociedade e por exemplo se o crescimento da renda per capita é um fator desejável os agentes vão locar recursos de modo a assegurar que essa variável Apresente uma tendência de crescimento ao longo do tempo e agora veja o exemplo da taxa de mortalidade infantil o fato de a sociedade desejar que essa variável diminua passa em que sua tendência seja decrescente ao longo do tempo e de certa forma a sociedade se mobiliza criando condições favoráveis para que essas trajetórias tem uma determinada direção persistente no caso da renda per capta
a sociedade investe em tecnologia produtividade fortalecimento das instituições no caso da taxa de mortalidade investe na qualificação dos Profissionais de Saúde em saneamento básico no sistema de saúde é obviamente que esse movimento e não acontece no curto prazo ele depende substancialmente das condições e do empenho da sociedade para fazer com que essas curvas persistam nessa trajetória existem dois tipos de tendências a determinística e a estocástica nesse primeiro momento vamos focar somente na determinística e a tendência determinística é uma variável temporal que pode ser utilizada como regressora em um modelo econométrico pressupomos que a variável dependente
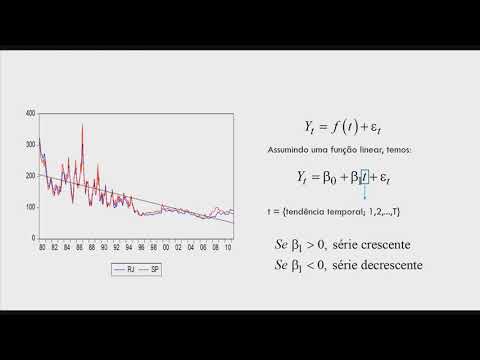
yt é uma função do tempo a forma funcional depende do objetivo e da referência teórica da pesquisa Mas normalmente Assumimos que essa função seja linear e o modelo de tendência determinística linear pode ser escrito por YP igual a Beta 0 mais Beta um t a variável B é uma sequência cronológica ela pode estar em anos trimestres meses ou pode ser simplesmente uma sequência de números inteiros que se inicia em um e termina no número que define a última observação da série por exemplo se a variável analisada em dois períodos a sede tempo te pode ser
iniciada em um e terminada em 12 e a partir disso estimamos um modelo econométrico por meio de n que ó para obter soluções numéricas para os parâmetros Beta 0 e beta um o coeficiente Beta 0 é uma estimativa do valor inicial da série mas sua interpretação normalmente não é o foco já o Beta um é muito importante porque ele representa a inclinação da tendência da variável se Batam por positivo isso quer dizer que a variável y te possui uma tendência de crescimento se Betão for negativo essa variável decresce ao longo do tempo vamos supor que
a variável y te esteja sendo analisada em meses e que após estimar o modelo encontramos a solução yt chapéu = 2 - 25 t e esse resultado mostra que a variável Y possui uma tendência de de crescimento porque o sinal do coeficiente que acompanha o tempo foi negativo além disso a gente pode dizer que a cada mês a variável Y diminuia cerca de 25 unidades em médio Ah tá mas e se o coeficiente da tendência não for significativo bom isso quer dizer que é variável Y não apresenta uma tendência determinística ou seja ela oscila em
torno de algum valor médio constante e em alguns casos a variável pode apresentar um padrão de tendência que cresce a taxas crescentes Veja por exemplo nessa figura que a variável de emissões CO2 observado aparentemente cresce mais rápido no início do que no final nesse caso o modelo de tendência linear numa oferece mais o melhor ajuste para série alternativamente A gente pode adotar o modelo de tendência quadrática basicamente construímos uma nova variável a partir da série definida cronologicamente essa nova variável é o quadrado de ter que é o tempo e depois que o modelo é estimado
a variação média de y no tempo vai depender do momento histórico que estamos analisando a série por exemplo se tem foi igual a um a taxa de crescimento de y vai ser Beta um mais duas vezes beta-2 se ter foi igual a dois essa taxa será beta-1 mais quatro vezes beta 2 tá em qual ponto do tempo a variável para de crescer para calcular isso dele vamos Y em função do tempo igualamos a 0 e resolvemos a expressão para ter nesse caso o ponto de máximo da série é observado no meio do T = -
Beta 1 sobre 2 beta 2 o mesmo raciocínio pode ser aplicado pela séries que decrescem com taxas variáveis e o ponto de mínimo também pode ser obtido da mesma forma e ainda em relação a esse gráfico perceba que nós temos aqui três séries a série observada prevista e o Rezende o resíduo dessa regressão representa o comportamento das emissões de CO2 quando a gente remove o efeito da tendência da variável o que a gente consegue perceber é que ainda um padrão sistemático um resíduo esse padrão quando está associada a UPS componente determinístico da série que são
a sazonalidade e o ciclo das emissões e vamos analisar agora aplicação do modelo de tendência a uma variável de vendas e pela análise gráfica vemos que a variável apresenta uma tendência de crescimento ao ajustar o modelo de tendência linear obtemos uma reta de regressão com inclinação constante a diferença entre as vendas observadas e previstas é o resido e novamente o resíduo representa as vendas quando controlámos o efeito da tendência após a se controle fica visível um outro tipo de comportamento da variável vendas agora avariaram se mostra como a trajetória de crescente até meados de 2007
período no qual a uma reversão sua dinâmica temporal Além disso recebemos também que existem períodos em que a série apresenta alguns Picos e ajustando o modelo de tendência quadrática vemos que a previsão e os resíduos assumem outras trajetórias a primeira coisa que a gente observa é que a série entrevista tá mais próxima da observado então a gente poderia dizer que o modelo tá mais bem ajustado aos dados já os resíduos aparentemente os irão próximos a zero mas os Picos em alguns meses continuam evidentes e até aqui a gente viu o modelo de tendência onde os
parâmetros são lineares mas existem algumas formulações da Economia em que esses parâmetros não são lineares a igreja a equação 1 um Y crece uma função exponencial do tempo a zero é o valor inicial R é a taxa de crescimento e t é o tempo esse modelo não pode ser estimado por ele que ó porque os parâmetros não são lineares preço demais modelo é necessário mineralizada equação para isso clicamos logaritmo Em ambos os lados pela propriedade dos logaritmos podemos reescrever o modelo como Y = log de a zero + log dos elementos que estão dentro do
colchetes podemos cancelar o logaritmo com o termo exponencial e escrever equação dessa fórmula agora veja que a variável login de y está em função de log de a zero mais rxp e como as LR são constantes podemos novamente reescrever a equação substituindo agora longo de ar o Beta 0 e r por Beta 1 e agora os parâmetros do modelo podem ser estimados por ele que outro o Beta um tem uma interpretação bem conhecida na economia esse coeficiente representa a taxa de crescimento instantânea da variável Y ou seja ele reflete a variação percentual média da variável
y ao longo do tempo a título de exemplo vamos supor que após estimar o modelo encontramos o seguinte resultado Como podemos interpretar o paralama do que acompanha um tempo dessa maneira a cada período a variável Y cresce em média 7,5 por cento é bom pessoal e se identifica por aqui até o próximo e bons estudos [Música] E aí
Related Videos

12:01
O que é sazonalidade?
economiaetv
5,337 views

9:36
Qual a diferença entre regressão e séries ...
Samuel Macêdo
8,351 views

30:19
Semana 1 - Introdução às séries temporais
Ricardo Buscariolli
6,290 views
![[PrevisãoDemanda] - Tendência e Sazonalidade](https://img.youtube.com/vi/PjRNnOhPO0A/mqdefault.jpg)
10:02
[PrevisãoDemanda] - Tendência e Sazonalidade
Felipe Tumenas
42,531 views

13:18
Aula 64: O Que é Análise de Séries Tempora...
Análise de Séries Temporais
646 views

10:28
Introdução a modelos de séries temporais (...
economiaetv
4,111 views

9:53
Séries Temporais no R
Professora Vanessa Manhães
10,918 views

28:37
Time series regression using Cochrane Orcu...
Mike Crowson
12,915 views

34:22
Introdução aos Modelos Auto regressivos - ...
Outspoken Market
6,121 views

20:13
Python - Análise de Séries Temporais - Méd...
Bruno Lima - PBIx
6,316 views

9:54
Médias Móveis Análise de Séries Temporais
Estatística para Concurso
3,332 views

6:15
O que é estacionariedade?
economiaetv
5,416 views

21:30
Conceitos de Séries Temporais - Outspoken ...
Outspoken Market
20,550 views

11:49
Planilha de Previsão no Excel 2016 - Como ...
Aprendendo Gestão
51,776 views

36:58
Aula 1 - Intro
José Augusto Fiorucci
16,977 views

34:45
Regressão de Séries Temporais
Análise Macro
2,505 views

15:02
Mostrando modelos ARIMA para análise de sé...
Análise de dados e metodologia de pesquisa
8,315 views

11:18
Aula 02: Não inicie a Análise de Séries Te...
Análise de Séries Temporais
6,632 views

4:12
Séries Temporais - Resumo - Parte 01
Monitoria Econometria II
4,323 views