Redes Neurais - Fundamentos e derivação do algoritmo de retropropagação
2.11k views3691 WordsCopy TextShare

UNIVESP
Nesta videoaula, o professor Marcos G. Quiles introduz o principal algoritmo da área, o algoritmo de...
Video Transcript:
[Música] Olá bem-vindos a oitava vídeo aula do curso de redes Morais artificiais nessa aula nós vamos apresentar a fundamentação do algoritmo de reto propagação e a derivação desse algoritmo de propagação ela vai ser uma aula um pouco mais densa que eu vou apresentar uma sequência de derivações uma sequência de aplicações da regra da cadeia da derivada para que nós consigamos atingir a derivar a forma de atualização de cada peso de uma rede neural com múltiplas camadas então nessa aula nós vamos fazer a introdução né entender a ideia Qual que é a fundamentação por trás do
algoritmo de propagação e a derivação desse algoritmo bom nós vimos na aula passada que essa rede aqui com duas camadas uma camada oculta e uma camada de saída resolve um problema não linear que é o problema chora que foi responsável inclusive pelo pessimismo aprontado pelo missky pelo Papa tinha uma década de 70 especificamente 69 né finalzinho da década de 60 é que levou ao Inverno da primeira inverno das redes neurais na década de 70 Então nós vamos ver agora como configurar esses parâmetros tanto dos neurônios ocultos quantos os neurônios da camada de saídas suas respectivas
baias a partir do algoritmo de retropropagação qual que é a ideia principal aqui na camada de saída eu consigo saber exatamente qual que é o valor desejado para aquela saída do neurônio então neurônio teve como saída apresentou como saída zero eu sei que a saída desejada é um eu consigo calcular de maneira explícita esse erro porém Qual que é a saída desejada para o neurônio da camada oculta se eu tivesse múltiplas camadas ocultas uma sequência de camadas qual que seria a saída desejada para cada um desses neurônios a gente não tem como calcular esse erro
ou a sair esperada para cada neurônio de forma explícita aí tá consequência uma das limitações que ficou durante muito tempo de como treinar essas redes com múltiplas camadas então algoritmo de retropropagação ele surgiu para resolver esse problema ele apresentou uma forma de como nós podemos calcular as derivadas de camada camada da camada de saída até a camada de entrada permitindo que essas esses neurônios das camadas anteriores também possam ser atualizados e o seu desenvolvimento mostrou que aquele pessimismo lá do misky em 1969 estavam errados ou seja nós podemos utilizar redes neurais para treinar para resolver
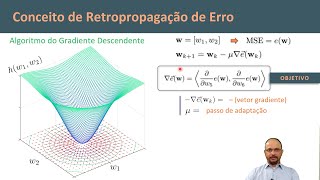
problemas não lineamento separados pelo menos mais complexos assim como choro e como já falei inúmeras vezes fomos algoritmos mais importantes aí motivou o ressurgimento pelo interesse da área na década de 80 bom qual foi a ideia o princípio do algoritmo de retropropagação ele vai partir também da regra Delta Ou seja a mesma regra que nós utilizamos lá numa modaline Ou seja a derivação o ajuste dos pesos de um peso do yésimo peso de um caésmo neurônio da rede vai ser dado a partir da derivada o sinal negativo né indicando que o gradiente descendente da derivada
parcial da energia do erro em relação aos pesos multiplicado pelo Eta que representa para a gente a nossa taxa de aprendizagem no qual a energia do erro nesse caso aqui representa o somatório quadrático dos erros de cada um dos neurônios da camada de saída podemos é importante frisar aqui que essa aqui é uma função possível mas existem diversas funções de custos que a gente pode utilizar qualquer ideia toda função de custo ela vai fornecer presente uma superfície e o que que a gente busca os mínimos dessa superfície ou seja os parâmetros que levam ao mínimo
daquela função de custo Então seja o erro quadrático médio função de entropia cruzada também é utilizada para a classificação e diversas outras que nós temos a literatura a ideia vai ser exatamente a mesma vai mudar Vai ser como que a gente deriva a função mas todas elas partem do Gradiente descendente para ajustar os pesos então aqui nós vamos precisar fazer o uso do nosso gráfico de fluxo então o que que nós sabemos fazer uma passagem geral por esse gráfico nós temos a saída da rede que gera um erro esse erro é quem é a saída
fornecida pelo neurônio comparado com o sinal desejado para aquele padrão então subtraindo desejado menos obtido nós temos o erro então o erro ele depende da saída do neurônio por sua vez a saída do neurônio depende do campo local induzido desse neurônio que passa pela função de ativação por sua vez o campo local induzido desse neurônio depende dos respectivos pesos e das suas entradas por sua vez é centrada específica dessa sinapse aqui é a saída de um neurônio parece sintático então eu posso falar que a energia do erro Ela depende da saída deória mas também depende
da saída de neurônio depende do Peso desse neurônio assim como dos neurônios anteriores camada a camada então para calcular essa derivada aqui nós precisaremos aplicar a regra da cadeia ao longo de todo esse gráfico de fluxo saindo da camada de saída e chegando a primeira camada na camada que primeira camada oculta posterior a camada de entrada então qualquer ideia vamos Primeiro começando aplicando a regra da cadeia de forma genérica eu tenho que o delta w Depende de -0 vezes a derivada parcial da energia do e relação aos pesos mas eu sei que antes de depender
dos pesos eu posso falar que o erro depende do campo local induzido do neurônica então a gente pode desmembrar o aplicar a regra da cadeia sobre essa derivada transformando ela na derivada parcial da energia do erro em relação ao campo local induzido do neurônio k multiplicado pela derivada parcial do campo local induzido neurônio cai em relação aos seus pesos resolvendo essas derivadas começando com essa segunda derivada que nós temos que o campo local induzido é o produto interno entre as entradas e suas respectivos pesos seu derivar em relação ao peso específico de j ou seja
a JS entrada do neurônio Car então nós já temos essa primeira derivada essa outra derivada que a energia a derivada parcial da energia do em relação ao campo local induzido nós vamos chamar ela de Delta minúsculo ou seja Delta do neurônio k esse Delta também é chamado por alguns autores de erro local do neurônio cardiente local do neurônio Car ou simplesmente Delta minúsculo de cá tá bom então substituindo isso aqui na nossa equação nós temos que a o delta a variação do peso do jéssimo peso do neurônio k vai depender de dieta vez o delta
do neurônio k vezes o XJ que alimenta aquela sinapse J do neurônio k Mas quem que esse deltacar né ela derivada parcial da energia do erro em relação ao campo local induzido do próprio neurônio que eu tô derivando como que a gente faz essa derivada novamente a gente fazer a aplicação da regra da cadeia em diversos Passos eu sei que a saída o erro do neurônio depende do campo local induzido mas o campo local induzido alimenta funciona ativação que gera a saída do neurônio Então posso falar que essa derivada aplicando a regra da cadeia pode
ser a derivada parcial da energia do em relação a saída do neurônio k por sua vez multiplicada pela derivada parcial da saída do neurônio cai em relação ao seu campo local induzido eu tô falando que a derivada parcial da saída em relação ao próprio argumento é a própria derivada da função de ativação Então você tem que Y uma geral da parte de F de V de k derivando isso aqui em relação a veia de k nós temos a própria derivada da função de ativação já esse termo aqui essa derivada ela vai depender da posição do
neurônio na rede porque se eu tô na camada de saída eu conheço o erro de forma explícita se eu tô na camada oculta eu não conheço o erro de forma explícita Então a gente vai ter que ver maneiras de como calcular esse erro para as unidades nas quais eu não consigo é definir explicitamente o erro de saída Então se a gente pensar na no neurônio de saída que é o nosso caso mais simples Aqui nós já Vimos que isso daqui representa para nós a derivada da opção de ativação aqui eu vou derivar então a energia
do erro em relação a saída do neurônio Car energia do erro é um meio do somatório dos erros quadráticos derivando isso daqui em relação ao Y da mesma forma que nós já fizemos para dar Line também vai sobrar duas vezes no meio corta o 2 o erro vezes menos um ou seja menos o erro de k então substituindo no Delta aqui o delta de cá vai ser o erro daquele neurônio multiplicado pela derivada da sua função de ativação então Delta do neurônio no carro quando o neurocar pertence à camada de saída exatamente o erro vezes
a derivada funciona de ativação Qual que é o erro do neurônio cultura eu não consigo derivar de maneira direta esse erro em relação à saída de um neurônio J que pertence uma camada anterior da rede então a gente aplicar sucessiva às vezes a regra da cadeia da derivada para conseguir chegar na fórmula analítica dessa derivada bom nós sabemos como já comentei né pelo processo supervisionado nós conhecemos o erro apenas na camada de saída do neurônio fornece uma saída eu comparo essa saída com o valor desejado e consigo calcular de maneira explícita esse erro bom o
neurônio k sai o erro na cama no neurônio Car ele depende internamente ele depende diretamente do campo local induzido da atividade interna desse Drone cá por sua vez esse estado interno o campo local depende dos seus respectivos pesos e das saídas dos neurônios que alimentaram esse neurônio Car ou seja neurônio j ou dois neurônios Jotas que antecedem a camada k que a gente está calculando como sendo a camada de saída portanto a gente pode falar que de alguma forma a saída desses neurônios da camada anterior elas influenciam no erro do neurônio da camada de saída
Então qual que é a nossa Nosso propósito aqui é tentar estimar o erro dos neurônios Jotas a partir do erro conhecido dos neurônios da camada k da camada posterior aí uma vez que eu conheço os erros desse neurônios da camada J eu posso utilizá-los para tentar estimar o erro de uma camada anterior e assim sucessivamente Até chegar na camada de entrada Vamos pensar o seguinte se eu tenho aqui minha camada de saída e aqui eu tenho um neurônio da camada oculta esse aqui é o delta minúsculo ou Gradiente local desse neurônio 1 que que eu
posso falar desse delta em relação essa saída yj aqui vamos pensar o seguinte se esse Delta aqui ele tem um valor muito baixo indicando um erro muito pequeno quer dizer que a resposta desse neurônio nenhum ela foi boa se ela foi boa e eu tenho um alto peso ligando esse neurônio há um neurônio anterior significa que essa saída anterior Possivelmente Foi boa também porque essa saída ela contribuiu em grande parte para a formação do Estado interno desse neurônio porque esse peso aqui é grande então de alguma forma a saída o erro ou acerto desse Drone
J ele depende do erro do neurônio da camada posterior e também do peso que liga esse neurônio a camada posterior é no outro caso se eu tenho um erro aqui desse neurônio é um erro muito baixo e esse peso é muito alto significa que esse essa saída aqui contribuiu muito para o estado interno desse terror e gerando um erro baixo logo esse neurônio também Possivelmente tem um erro baixo e se quando esse peso ele é muito pequeno que que eu posso falar do neurônio anterior que basicamente ele influencia muito pouco esse neurônio então o erro
dele depende de pouco do erro desse da camada posterior Então como que fica isso para que a gente aplica a regra da cadeia da derivada da cadeia da derivada Vamos lá nós queremos calcular o nosso Delta do neurônio J Lembrando que agora o J ele não pertence mais a camada de saída ele pertence uma camada anterior então a derivada parcial da energia do e relação ao campo local induzido a gente já viu que a gente pode desmembrar ela como sendo derivada parcial da energia do erro em relação a saída do J e as derivada parcial
da energia do neurônio J em relação desculpa da saída do J em relação ao seu campo local induzido essa segunda derivada aqui ela é própria derivada da função de ativação do neurônio J então isso aqui a gente já tem calculado de maneira direta agora o nosso problema tá aqui como calcular a derivada parcial da energia do erro em relação a uma saída yj de um neurônio de uma camada anterior então quem que é a energia do erro é o somatório quadrático dos erros dos neurônios da camada de saída dos neurônios da camada k então o
seu derivai isso daqui em relação ao yj a gente vai ter duas vezes o meio vezes o edcar vezes a derivada do Edgar em relação ao yj Então essa derivada aqui vai ser representada por esse termo aqui juntando tudo nós temos que o delta minúsculo de J vai ser menos a derivada da função ativação de J multiplicada pelo somatório dos erros dos neurônios da camada posterior k multiplicados pela derivada parcial da energia do erro desse neurônio Car em relação à saída do neunoj ou seja existe ainda uma derivada aqui que nós precisamos resolver ela bom
Então como que a gente pode desenvolver resolver essa derivada novamente não vamos aplicar a regras da cadeia tudo todas as cadeias essa regra da cadeia que eu tô aplicando ela pode ser acompanhada pelo gráfico de fluxo do neurônio tô pegando uma saída que depende de outra que depende de outra a partir do gráfico a gente consegue verificar a relação de dependência entre esses Entre esses termos então a derivada parcial do erro em relação à saída do J A gente pode falar que ela é derivada parcial do erro em relação ao campo local induzido de um
neurônio lá da camada de saída de neurônio k vezes a derivada parcial do campo local induzido pela derivada pela derivada parcial da saída do neurônio J que é quem alimenta o neurônio do carro então eu tô falando que o campo local induzido dono neurônio k depende da saída do neurônio J é como que a gente calcula a saída o campo local induzido neurônio k é o somatório ponderado das entradas seu derivai isso daqui em relação ao yj específico sobra apenas o w de kj que é o que tá aqui essa outra derivada eu preciso derivar
então a o erro do neurônio Car em relação ao campo local induzido específico Quem que é o erro do neurônio k é o desejado menos obtido sendo que obtido é a própria função ativação alimentada pelo pelo campo local induzido seu deriva isso daqui em relação ao verticar Isso aqui é uma constante corta vai ficar menos a derivada da função de ativação do neurônio k dever de cá então substituindo tudo isso a todas essas derivadas calculadas na nossa forma de atualização nós temos que o delta minúsculo de J vai ser a derivado da função ativação do
próprio neurônio J vezes o somatório ponderado dos erros dos neurônios da camada k vezes a derivada da função ativação sobre aquele neurolocar ponderada pelo peso que liga o neurônio cá ao próprio neurônio J como é de cá a vez a derivada da função ativação do próprio neurônio a gente já viu que isso pode ser representado por Delta minúsculo de cá a gente pode substituir esse pedaço da equação por Delta de caqui então nós temos que o delta de J vai ser o quê o somatório ponderado dos deltas da camada posterior ponderado pelos pesos vezes a
própria derivada da função ativação do neurônio que eu tô calculando naquele momento aí uma vez que eu calculei os deltas dessa camada aqui eu posso replicar o processo e utilizar esses Delta JJ para calcular os Delta de uma camada anterior fazendo isso sucessivamente Até chegar na camada de entrada então basicamente isso é a ideia do algoritmo de propagação a gente vai sair da camada de saída calcular os deltas de maneira explícita no qual nós conhecemos o erro é uma vez que eu tenho esses deltas calculados a gente vai tentar estimar o delta da camada anterior
utilizando o somatório ponderado dos deltas da camada posterior vez a derivada ele funciona a ativação desse nome a hora que eu calculo os deltas dessas dessa última camada oculta eu consigo utilizar esses deltas para calcular os deltas da camada que antecede essa camada oculta e assim até chegar na camada de entrada então para atualizar os neurônios nós temos que a forma de atualização geral é isso daqui né que é o delta é w kj é o Eta que a taxa de aprendizagem vezes o delta vezes a entrada J dessa sinapse para a camada de saída
o deltak é calculado de maneira explícita derivada ela funciona ativação vezes o erro de cá e para os neurônios da camada oculta a gente sempre precisa dos deltas da camada posterior então a gente calcula esse somatório ponderado desses deltas da camada posterior multiplicado pelo X que alimenta aquela sinapse vez a derivada era profissional de ativação do próprio neurônio então algoritmo de propagação ele funcionar em duas fases principais primeiro tem a gente tem a fase Fit faword ou fase adiante a fase de propagação do qual nós vamos apresentar um padrão para entrada da rede esse padrão
vai ser no propagado camada camada Até chegar na camada de saída cheguei na camada de saída eu consigo calcular os erros esse erro multiplicado pela derivada da função de ativação é o delta minúsculo esse δ eu consigo reto propagar ele na nossa fase 2 que a fase de feedback ou fase de retorno fase de retropropagação dependendo do autor Então vou reto propagar esse erro esse Delta da camada de saída até a camada de entrada e uma vez que eu tenho os deltas calculados eu consigo atualizar os pesos porque a atualização do Peso nada mais é
do que o Eta vezes o delta vezes a entrada daquela sinapse então algoritmo de retopropagação o que que ele permite ele permite nós conseguimos estimar a qual que é o delta Qual que é o erro local de cada neurônio da camada oculta sem necessariamente conhecê-lo de maneira explícita ele vai ser uma estimativa a partir dos erros calculados na camada posterior Então tá aqui nossa uma estrutura possível da rede Multilaser Lembrando que Nesse caso tem duas camadas ocultas mas eu poderia ter uma duas três n camadas ocultas ligando a camada de entrada até a camada de
saída então na fase de propagação ou fase adiante a gente vai sair da camada de entrada e propagar o sinal até a camada de saída aqui nós computamos os erros e depois reto por pagamos esses erros da camada de saída até a camada de entrada corrigindo todos os pesos todos os parâmetros desses neurônios Então como que eu como que é algoritmo funciona de maneira geral nós temos a inicialização dos hiper parâmetros dos modelos que que seria o zíper parâmetros Aqui nós temos duas camadas ocultas com cinco neurônios essa primeira camada e três neurônios nessa segunda
camada oculta eu poderia ter três camadas poderia ter 10 neurônios na segunda camada Então essa quantidade de camadas quantidade de neurônios Assim como as taxas utilizadas taxa de aprendizagem outras taxas que a gente vai ver em outros algoritmos elas podem ser consideradas e preparamos da rede Então isso que eu defini Quais são os parâmetros Qual que é o tipo de topologia que eu vou utilizar na rede é uma rede com nitradas y saídas eu tenho tantas camadas ocultas com uma quantidade específica de neurônios em cada uma delas então com base nisso eu vou configurar os
pesos iniciais essa rede geralmente de forma aleatória e a gente vai iniciar o treinamento dessa rede é aplicando o padrão a padrão fazendo a propagação e a reto propagação atualizando os pesos até o momento que a gente consiga atingir um erro mínimo aceitável o mesmo erro 0 se a gente conseguir criar uma fronteira de separação que separa de maneira precisa as duas classes que eu tenho as n Class que eu tenho nesse problema então primeiro a gente vai pegar um padrão do nosso conjunto de dados apresentar na entrada da rede esse padrão vai ser propagado
camada camada Até chegar na camada de saída lá nosso calculamos o erro e a gente uma vez que eu tenho esse calculado a gente reto propaga esse erro da camada de saída até a camada de entrada atualizamos os pesos de cada processador ou seja cada uma daquelas arestas cada peso associado a cada neurônio e a gente volta ao passo 1 até atingir uma quantidade máxima de épocas estabelecidas ou até atingir aquele erro de tolerância aceitável bom que que nós vimos nessa aula então nós compreendemos os fundamentos do algoritmo da propagação e nós entendemos como que
como que a gente chega a partir da derivada da energia do e relação aos parâmetros do cálculo de atualização de cada peso da rede seja ele de um neurônio de saída ou de um neurônio na próxima vídeo aula vai ser uma aula um pouco diferente vai ser uma aula prática no qual vou mostrar para vocês utilizando a linguagem Python o funcionamento de uma de uma rede neural do tipo Multilaser o funcionamento e treinamento dessa Rede Bom Agradeço a todos pela atenção até a próxima aula [Música] [Música]
Related Videos

22:55
Redes Neurais - Exemplos práticos de imple...
UNIVESP
2,129 views
24:41
Projetos de Redes Neurais - Parte 03: Conc...
Pratique IA
668 views

7:47
Question about Fungi - General Characteris...
BIOLOGIA com o TUBARÃO
8 views

POWERFUL DEEP HEALING MUSIC 432Hz | Super ...
Sallay

14:29
Como uma Rede Neural Aprende? Tutorial par...
Escola de Inteligência Artificial
79,257 views

18:19
Por que o BRASIL não tem TRENS?
Ciência Todo Dia
586,583 views

14:55
Por que o CHOCOLATE FICOU TÃO RUIM?
Olá, Ciência!
368,459 views

9:51
Congresswoman Jasmine Crockett on Trump Ca...
Jimmy Kimmel Live
1,048,614 views

11:54
Lawrence: China sees 'world's biggest clow...
MSNBC
1,154,186 views

17:34
Neural Networks Pt. 2: Backpropagation Mai...
StatQuest with Josh Starmer
623,522 views

51:41
Webconferência - ENADE 2023
UNIVESP
900 views

15:43
Oops!: Trump's first 100 days marked by in...
MSNBC
507,105 views

11:55
Happy Easter And 4/20 | The Trump Whispere...
The Late Show with Stephen Colbert
2,670,520 views

10:42
‘He’s been exposed’: Tesla flounders as El...
MSNBC
479,935 views

13:25
Hegseth SLAMS Leakers After Text Fallout &...
Jimmy Kimmel Live
2,123,609 views

19:29
Backpropagation : Data Science Concepts
ritvikmath
48,243 views

17:55
INTRODUCAO AOS METODOS INSTRUMENTAIS
QUÍMICA+
987 views

10:28
Backpropagation descomplicated
Sandeco
27,298 views

49:13
BREAKING NEWS: Trump Takes Multiple Questi...
Forbes Breaking News
333,987 views

23:08
There's No Bishop Pair Like Ivanchuk's Bis...
agadmator's Chess Channel
60,678 views