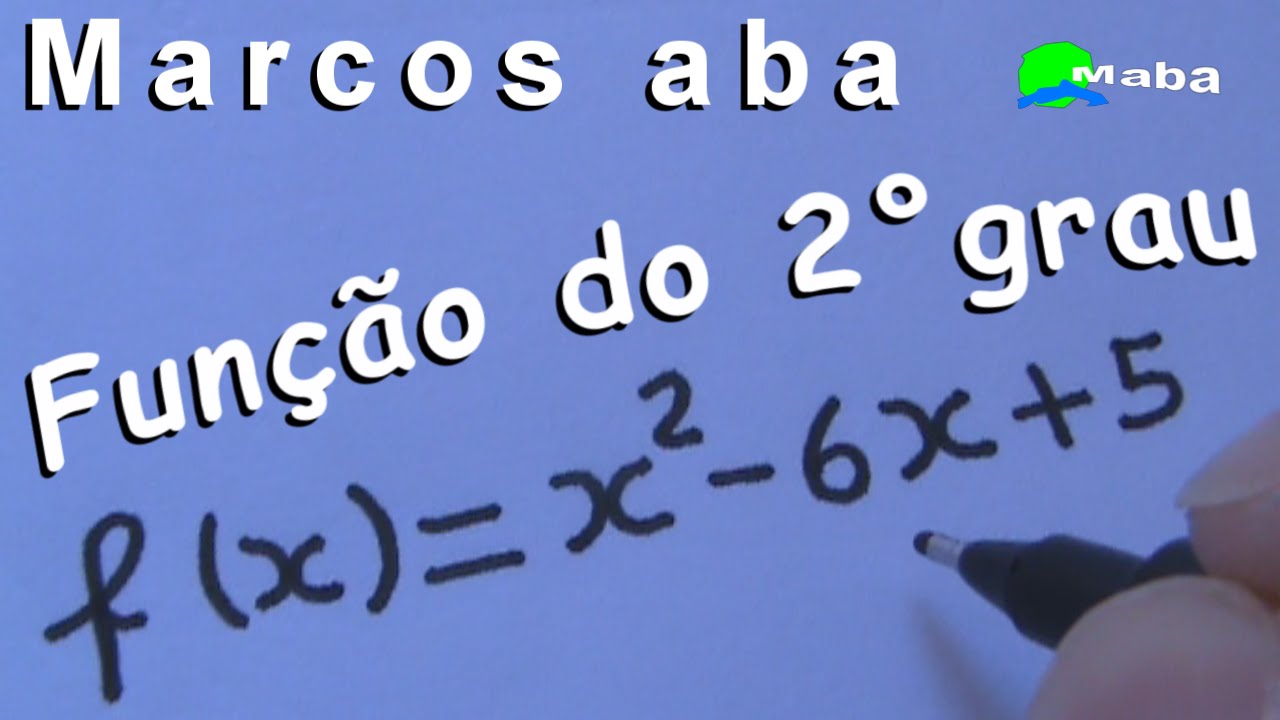FUNÇÃO DO 2º GRAU | FÁCIL E RÁPIDO

fala frente deu pleno vídeo vem até o final aprender função de segundo grau esse vídeo vai ser diferente eu vou explicar direto eu vou apagar e continuar explicando e não tem corte acabou o vídeo você aprendeu lembrando quer estudar comigo no curso completo de matemática do zero ao topo clica aí na descrição e vem vamos nessa função de segundo grau a estrutura eu tenho incógnita elevada ao segundo grau é o maior grau que eu tenho da função curió E aí qual é a condição para uma função sexto segundo grau é o termo isso mesmo coeficiente

que acompanha o x ao quadrado ser diferente de zero ele tem que existir sendo diferente de zero curiosa já dá um exemplo que tua aula é assim é sempre com exemplos Claro achemy para que seja do segundo grau ou seja acho o valor de m aqui para que essa função seja de segundo grau aqui ó eu o termo de segundo grau tendo coeficiente com a incógnita M que que eu vou fazer o que tá acompanhando x ao quadrado eu vou falar que ele tem que ser diferente de zero que essa é a condição e se

você assistiu o vídeo de equação do segundo grau você sabe resolver aqui ó M ao quadrado diferente de 4 que eu passei para cá M diferente de mais ou menos raiz quadrada de 4 não esquece do mais ou menos logo M diferente demais ou menos dois para todos os outros valores reais de m você tem essa função sendo de segundo grau não podendo ser o dois e o -2 curió essa parte eu peguei agora eu quero aprender com cavidade Eu quero achar as raízes de uma função do segundo grau e eu quero saber construir o

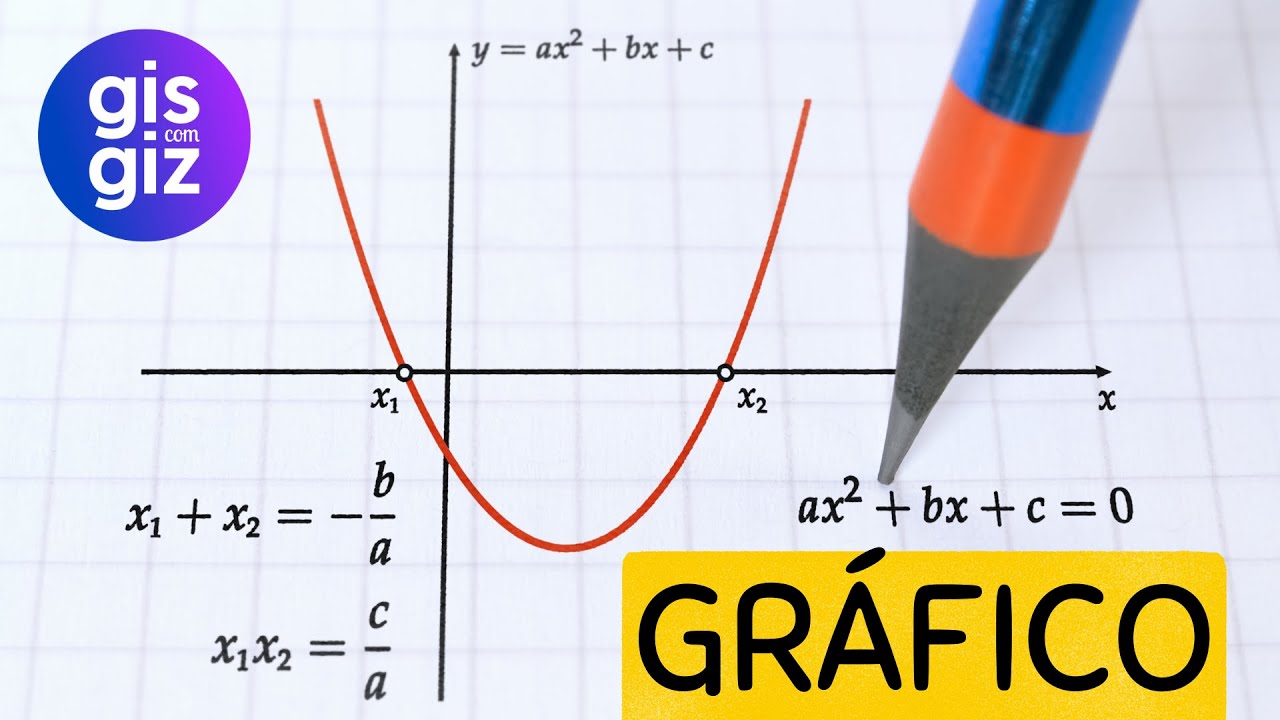
gráfico inclusive falou de função máximo mínimo eu fico perdido Vai vendo esse vídeo vamos nessa a concavidade pode estar com cavidade da parábola que é o gráfico da função do segundo grau é o valor do coeficiente a é o coeficiente do termo de segundo grau curió Como assim você vai guardar o seguinte ó se o a for positivo a parábola vai estar sorrindo A positivo parábola sorrindo e o curió ficou igual uma carinha aqui ó vou botar até o topetinho nele perfeito a maior que zero parábola sorrindo e se tiver negativo aí é triste Friends

a negativo a menor que zero a parábola tá com cavidade voltada para baixo ela tá triste aqui eu vou fazer uma Franjinha nesse daqui pegou Então não esquece mais a maior que zero positivo a com cavidade da parábola voltada para cima sorrindo a menor que zero negativo o valor de a com cavidade da parábola voltada para baixo triste negativo como achar as raízes da função Friends é super importante saber achar as raízes da função até porque você precisa construir o gráfico ou saber os valores que anulam a função logo eu preciso achar as raízes e

para as raízes você aprendeu lá né o a=1 o b menos 6 e o c é 5 você aprendeu a fazer máscara a equação do segundo grau você primeiro igual a zero que a intenção é achar as raízes se achar as raízes Você quer os valores de x que anulam a função logo eu vou pegar o y que é o valor da função e vou chamar de zero igualando eu tenho o quê aqui você está diante de uma equação do segundo grau que se você não lembra eu vou resolver por Bhaskara para você e na

sequência aqui eu vou construir o gráfico dessa função perfeito Então vamos nessa achando as raízes primeiro eu vou achar o valor de Delta quer b² - 4ac substituindo b o a o c eu tenho aqui ó -6² - 4 x 1 x c que é 5 ficou um valor agradável por quê - 6² é 36 e esse produto dá 20 dando Delta um número quadrado perfeito 16 achei 16 eu venho aqui para achar as raízes ó x = - b mais ou menos raiz de Delta sobre duas vezes a E aí eu vou achar as

raízes aqui sendo um e cinco fazendo essa conta as raízes vão dar 1 e 5 curió achei a solução Achei as raízes deu um deu cinco perfeito mas eu quero saber como construir o gráfico de uma função de segundo grau vou dar o delete aqui nessa parte que nós já vimos e vou construir para você o gráfico da função do segundo grau curió como você vai hidrográfico primeiro eu vou te dar umas dicas aqui ó o gráfico o foco é construir o gráfico Como eu disse Esse vídeo é direto dessa função aqui ó x ao

quadrado menos 6x + 5 para construir o gráfico da função você vai fazer o seguinte o primeiro passo você vai verificar se a parábola está sorrindo ou triste é com cavidade se ela sorrir que nós já vimos com topetinho ou se ela fica triste que nós já vimos com a Franjinha o segundo passo Olha o bizu Não esquece você vai fazer o seguinte você vai achar as raízes isso mesmo vai achar as raízes da função curió porque achar as raízes porque as raízes elas cortam o eixo X então quando você acha as raízes seja ela

sorrindo ou triste você passa até essa informação aqui ó se ela sorrindo Você tem os pontos onde elas cortam as raízes onde a parábola corta as raízes o mesmo estando triste ó vai cortar aqui e aqui pegou Então essa importância de achar as raízes da parábola curió mais um bizu para eu não esquecer o terceiro passo Friends não esqueça quando você for construir o gráfico de uma função de segundo grau sempre a parábola vai cortar o eixo Y no valor de ser coroa é mentira te digo verdade sempre a parábola vai cortar o eixo Y

no valor de criou dar um exemplo se eu tenho uma parábola aqui eu posso afirmar que ela corta no valor do c do termo independente exatamente então curiosa aqui não tem esse x né então eu posso afirmar que aqui ó o ser igual a 5 logo a parábola vai cortar o eixo Y no cinco sim esse vai ser o gráfico nós vamos construir e por último eu vou explicar para você as o valor de máximo e mínimo da função tá então já expliquei isso daqui de sorrindo e triste Vou encaixar aqui o quarto passo primeiro

segundo terceiro e quarto passo para construirmos o gráfico o quarto passo é você achar o vértice da parábola curioso vértice da parábola é onde ocorre o quê onde ela muda de sentido e o vértice é um ponto né dela onde tem duas coordenadas o x do vértice e o y do vértice eu vou botar aqui para você não esquecer ó x do vértice menos B sobre 2 a e y do vértice - δ / 4 a é importante você guardar essa estrutura Mas vamos lá vamos construir os gráficos Lembrando que eu já achei as raízes

tá Vou botar aqui para você as raízes foram um e cinco perfeito agora agora vamos nessa seguindo passo a passo como achar o gráfico dessa função que aqui está primeira coisa que você vai fazer você tem aqui ó o eixo Y e o eixo X perfeito ABC sabe X é o x y ordenada vamos seguir os passos primeiro a parábola sorrir ou está triste x ao quadrado menos C x + 5 o valor de a é 1 C é 1 eu já vou fazer essa anotação aqui no canto só é igual Ele é positivo a

parábola está sorrindo segundo passo vamos achar as raízes dessa função como eu acho as raízes igual a da Zero nós fizemos ela aqui e tivemos como resposta 1 e 5 você vai na sua prova e vai marcar um dois três quatro cinco seguindo um bom senso de distância terceiro nós vamos ver onde é que o gráfico cortar corta o eixo Y Ele vai cortar o eixo Y no valor de c o c não é 5 você pode afirmar que ele vai cortar o eixo Y no 5 coroa já posso botar o gráfico Claro tá aqui

ó esboça aqui ó já tá aqui seu gráfico esboçado ó só que ele desce até onde ah aí vem a pergunta crucial ele desce até o vértice da parábola e como eu acho vértice calculando o x do vértice o y do vértice mas eu vou te dar um bizu Mas vamos lá se fosse calcular o x do vértice é menos B Olha quem é o b nós já Vimos a o b menos 6 é menos B sobre duas vezes a o a tá aqui ó o a é um então duas vezes um x do vértice

menos com menos dá mais e 6 sobre 2 resposta 3 tá aqui ó desce desce desce achei aqui ó x do vértice porque o vértice ele tem duas coordenadas lembra o x do vértice do vértice achamos o x do vértice agora basta achar o y do vértice que eu vou jogar aqui ó Y do vértice é igual a menos Delta o delta tinha dado 16 então é menos 16 sobre 4 x 1 e menos dividido por mais dá menos resposta menos quatro é o meu Y do vértice pegou e assim nós construímos o gráfico da

parábola em Quatro Passos curiosa entendi perfeitamente só que tira uma dúvida eu posso afirmar que o x do vértice ele é sempre equidistante das duas raízes sim você pode afirmar que x do vértice ele estará sempre no meio ele tem a mesma distância entre as duas raízes pegou dá o print o quadro É e vamos para a próxima curió fala a próxima aí parte que você vai falar o pessoal tem muita dificuldade em ver o valor máximo e o valor mínimo da função tá é algo que cai muito em prova do ensino médio concurso vestibulares

e a galera tem dificuldade Então vamos nessa presta atenção no bizu que eu vou te dar só que antes eu vou falar o seguinte para você lembra daquilo Delta maior que zero tem duas raízes reais e distintas Delta igual a zero duas raízes reais e Iguais Delta menor que zero não admite raiz real não tem raiz real isso é algo muito importante também curar então criou a tabela para mim agora vou botar aqui para você ó para você não esquecer tá as duas situações é quando o a é positivo e quando há for negativo tá

então antes de falar de máximo e mínimo anota esse besouro aí que eu vou dar para você aqui então tá aqui ó A positivo e a negativo curioso ficou top esse quadro Obrigado vamos nessa tá aqui ó Delta maior que zero você tem a parábola cortando eixo X em dois pontos por quê tem duas raízes reais e distintas ó X1 e X2 se ele for negativo lembra que é triste então é mesmo uma situação ó vai ter o eixo X só que estará triste cortando também em X1 X2 curiosos tudo de sinais como eu faria

gráficos acima do eixo X função positiva abaixo aqui negativa aqui ó o contrário negativo na extremidade e positivo no meio curou mas se delta foi igual a zero se for igual a zero as raízes são reais iguais ela toca o eixo X no caso a parábola em apenas um ponto ela sorrir na coluna da Positivo tocando o x onde são as raízes na verdade elas são iguais em apenas um ponto curioso se tiver triste é o mesmo procedimento ela tá triste tocando em apenas um ponto porque eu estou na situação do Delta igual a zero

raízes reais e Iguais curioso Delta menor que zero não tem raiz real exatamente nos reais Delta menor que zero não tem raiz real se não tem raiz real que que vai a parábola faz ela fica voando sorrindo e no triste também ela fica voando Como assim voando ela não toca o eixo X até porque ela toca onde nas raízes se não tem raiz real ela não toca sendo aqui ó os sinais sempre positivo e aqui sempre negativo aqui ó mais mais aqui menos menos pegou esse é o Néctar Supremo dá o print aqui e eu

já vou falar para você de valores máximos e mínimos da função valor máximo da função muito importante esse hein cai direto e valor mínimo da função que que é da função cru é o máximo de y e o valor mínimo de y presta atenção que é muito importante isso sempre que a prova pedir a você qual o valor máximo da função ou qual o valor mínimo da função você vai achar o y do vértice aí você fala quando é uma mentira te digo verdade então pedir o valor máximo da função ou mínima é o y

do vértice porque quem vai dizer se ela tem valor máximo mínimo é o ar Como assim valor máximo da função Qual o valor máximo a parábola com certeza que ela estaria triste E aí se ela está triste ela tem um pico guarda isso ah curiosa nunca vou esquecer se ela tá triste ela é um morrinho E se ela é um morrinho ela tem um pico e nesse pico é onde você acha o valor máximo da função que por sinal é o y do vértice Quando me refiro a função é sempre Y pegou função é sempre

y a colher quando eu acharia o x do vértice se te pedisse o seguinte qual o valor de X torna a função máxima Aí sim é diferente de eu te pedir Qual o valor máximo da função valor máximo da função pode anotar Isso é só achar o y do vértice cura mais e se pedir Qual o valor mínimo da função Com certeza para ele te pedir um valor mínimo ela tá sorrindo e se ela tá sorrindo ela não tem mais um pico ela tem um vale se ela tem um vale Com certeza essa função terá

um valor mínimo que também vai ser calculado através do Y do vértice então o que que eu quero que você guarde nesse momento pediu o valor máximo da função ou pediu o valor mínimo da função você vai calcular o y do vértice que é menos Delta sobre 4a pode anotar coroa me dá um exemplo aí vou te dar um exemplo agora que cai muito em prova dá o print quadro é seu e olha o exemplo que eu vou te dar esse exemplo aqui ó cai demais em prova essa questão que eu vou anotar para você

de máximo e mínimo é o seguinte fala que tem um canhão aqui ó e esse canhão disparam projétil o projeto faz aqui assim ele fala que tem altura né e aqui é o tempo tá tempo em segundos altura em metros você já deve ter visto essa questão o canhãozinho tá aqui apontando para cima e eles para o projeto beleza ele fala para mim que a função desse projétil é descrita né a trajetória através dessa função aqui ó perfeito e ele pede para você lerei qual a altura máxima do projeto Qual a altura máxima do projétil

no caso disparado pelo canhão e a leribi Qual o instante a atenção Qual o instante em que o projétil que o projeto atinge sua altura máxima em qual qual é o instante em que o projétil atinge sua altura máxima Friends essa questão cai demais em Provas fiz agora para você como eu disse a aula ia ser direto sem interrupções Então vamos nessa cruel como é mesmo uma questão sabendo que a altura em metros e o tempo em segundos e um projeto é disparado por um canhão de escrevendo a trajetória dessa função determine para mim qual

a altura máxima do projeto primeiro observação que você ia ter é que aquela função do segundo grau onde eu tenho o a menos um o b 8 e o c é nulo e é importante você saber também o seguinte ó O a é negativo só é menor que zero a parábola é triste se ela é triste ela tem um pico lembra que eu falei para você tá aqui ó o pico e nesse pico eu consigo achar o valor máximo da função que por sinal o valor máximo dela é quem é a altura máxima se a

autora máxima que você vai achar você vai achar Com certeza o y do vértice tendo em vista que o pico é o vértice como eu te prometi Então qual é a altura máxima altura não funciona como Y por sinal é quem está isolado aqui a altura logo eu quero valor máximo da função e o curió disse que sempre que eu quiser o valor máximo eu vou achar o y do vértice que é menos Delta sobre 4a perfeito você vem aqui acha o delta ó é B ao quadrado menos 4 vezes a vezes c o c

sendo zero você já anula toda essa parte aqui e o delta fica B ao quadrado ou seja 8 ao quadrado Delta é 64 eu venho aqui substituir - 64 sobre 4 vezes a e o a menos um menos dividido por menos dá mais 64 / 4 16 metros é a altura máxima projeto curou a mentira que eu já calculei te digo verdade é isso e se pedir para mim qual o instante em que o projétil atinge sua altura máxima então projétil atinge sua altura máxima em que instante reparem você deve observar o gráfico o eixo

Y que é o da função é a altura e o eixo X Ele corresponde essas incógnitas é o tempo em segundos logo eu estou te perguntando em que instante ou seja qual é o tempo que o projétil atinge a autora máxima logo eu quero o x do vértice o valor de x que torna autora máxima Essa foi a pergunta e você calcula aqui ó x do vértice - B sobre dois a menos 8 sobre duas vezes menos um menos por menos dá mais e 8 sobre 2 o instante de 4 Segundos após o disparo o

projétil atinge altura máxima frente Esse foi o vídeo de função de segundo grau o Néctar supremo para você aprender com o método curió lembrando quer estudar comigo no curso de matemática começa na base matemática do zero ao topo é só clicar na descrição e vir com aulas ao vivo simulados monitoria diariamente muito mais para sua aprovação dá o print o quadro é seu Valeu em frente [Música]