A SEQUÊNCIA DE FIBONACCI e o NÚMERO DE OURO (razão áurea)
237.18k views1957 WordsCopy TextShare

Tem Ciência
Números de Fibonacci estão entre os mais famosos dentro da matemática. E principalmente fora dela! A...
Video Transcript:
no vídeo de hoje nós vamos falar sobre a sequência de Fibonacci e entender porque os seus números são conhecidos como os mais importantes da natureza e como eles se relacionam com o chamado número de Deus o número de ouro Muito provavelmente você já ouviu falar na sequência de Fibonacci ela é uma sequência de números naturais formadas a partir de uma regra bastante simples começando com um e um os termos seguintes são obtidos somando os dois termos anteriores assim o próximo termo é 2 = 1 + 1 depois 3 = 2 + 1 depois 5 =
10 + 2 e por aí vai se chamarmos de FDN o termo geral da sequência ou seja f de um F de 2 é um fd-3 é dois e etc então A Regra geral de formação da sequência de Fibonacci FD n = FDN menos um mais FDN menos dois Apesar do nome de ficou Naty Quem foi Leonardo Fibonacci Quem descobriu a famosa você conheça Aliás figurati nem era o nome verdadeiro dele mas a gente vai chamar tio Bonatti mesmo assim para descobrirmos então De onde veio a tal sequência vamos conhecer um pouco mais da história
do fibonattis rebonatti nasceu por volta de a 1.170 na cidade italiana de Pisa e era filho de um representante comercial que viajava muito ainda criança chocolate acompanhou o pai numa viagem de trabalho Argélia e lá ele começou a aprender a matemática indiana a matemática que ficou na tia atendia era de grande aplicação em contabilidade é uma ferramenta indispensável para Comerciantes naquela época a Europa ainda usava o sistema de numeração romana você já tentou fazer uma conta com algarismos romanos que o Bonatti Aprendeu o sistema de numerais indo-arábicos esses que a gente usa hoje em dia
e eles facilitam enormemente a realização de contas usando o sistema de posição Além disso Libonati também foi 10 ninguém mais ninguém menos que zero nas suas viagens fibonattis conheceu muitos problemas da Matemática indiana um deles que já era conhecido no Oriente vários séculos antes de fio Bonatti era calcular de quantas maneiras diferentes podemos organizar fonemas curtos e longos na poesias Anchieta a solução está numa certa sequência essa mesma que você está pensando ao retornar de viagem Libonati pegou todos esses conhecimentos que aprendeu nas suas viagens com o pai em escrever um livro chamado Liber abaci
no ano de 1202 esse livro trouxe uma verdadeira revolução para matemática europeia introduzindo o zero e demais numerais indo-arábicos que permitiram o desenvolvimento de toda a matemática moderna por isso o Liber abaci é considerado a obra matemática mais influente na Europa desde os elementos de Euclides escrito mais de mil anos antes um dos Capítulos e era baseado em pequenos problemas um deles era sobre uma população de coelhos o problema é o seguinte um homem coloca um par de coelhos jovens uma região cercada por muros um cativeiro bom com os pares de coelhos podem ser produzidos
a partir de separe um ano supondo que a cada mês cada para adulto gera um novo par jovem e que jovens coelhos levam um mês para se tornarem adultos e começaram a se reproduzir formando um novo par a cada mês irmãos que se amam bastante esse problema dos Coelhos estudiosa os presos no cativeiro é reprovável por vários pontos de vista mas o que mais importa aqui é que ele é biologicamente e realista então ao invés de falar dele vamos falar de outro problema que no final das contas é matematicamente idêntico mas é biologicamente correto a
ancestralidade de cromossomos X em seres humanos ele mostra uma importante conexão da sequência de Fibonacci com a natureza awnnn o nosso DNA só que nós vamos deixar para falar isso um pouco mais adiante Segurei o interesse dos matemáticos na sequência de Fibonacci não está no problema dos Coelhos e muito menos um problema de cromossomos já que essa é uma aplicação bastante recente desses números os matemáticos não precisam de mais do que a própria sequência de Fibonacci para ficar interessados já que ela esconde muitas propriedades curiosas você deve se lembrar que a sequência formada somando-se os
dois termos anteriores vamos ver então cinco propriedades interessantes aliás cinco é um número de chocolate e coincidentemente é o quinto número de chocolate eu não comecei ainda está aí no conto enfim vamos as propriedades primeiro se a dividir bebê Então os seus termos de Fibonacci correspondente também se dividem isso é é pedir a dividir fdb segunda o máximo divisor comum de dois números de Fibonacci é outro número de Fibonacci terceira todo número inteiro positivo pode ser representado a única como a soma de números de Fibonacci distintos porta um terço dos números de Fibonacci é par
um 4 é múltiplo de 315 é múltiplo de 5 e de modo geral um sobre n é um número de múltiplos de FDN dentro da sequência proporcionalmente e quinto os números de Fibonacci aparecem nas diagonais do Triângulo de Pascal a soma dos termos da Diagonal rasas sempre é um número de Fibonacci sabemos bastante coisa sobre a sequência de chocolate mas não sabemos tudo por exemplo diversos números de Fibonacci são primos os primeiros estão aí na tela computadores potentes já calcularam números primos de Fibonacci com milhares de dígitos o que ninguém sabe dizer até hoje é
se existem ou não infinitos números primos na sequência de chocolate Aliás se você souber posta aí nos comentários e escreve também o artigo que é mais apropriado de todas as propriedades matemáticas os números de Fibonacci a mais importante foi E aí o Husky ler aquele mesmo da astronomia Ele olhou para a sequência de Fibonacci e começou a calcular a razão entre termos adjacentes um sobre um da 12 sobre um dois três sobre dois dá um e-mail cinco sobre três da 1.666 E por aí vai então quebra percebeu que conforme ele percorria a sequência de Fibonacci
tomando termos cada vez maiores a razão de FDN mais um sobre FDN se aproximava cada vez mais de 1,618 03399 cada vez mais essa razão se aproximava de um mais raiz de 5 sobre 2 cada vez mais ela se aproximava de fi o número de ouro a relação entre números de Fibonacci e o número de ouro não acaba por aí explorando a relação de recorrência que dá origem a sequência é possível calcular uma fórmula fechada para o termo Geral de um número de Fibonacci e essa fórmula depende diretamente do número de ouro o número de
ouro é conhecido como o número de Deus e sua relação íntima com a sequência de Fibonacci arte nos ajuda a entender porque essa sequência é tão comum na natureza por exemplo a ramificação de árvores as espirais de abacaxi o crescimento das Folhas das alcachofras a genealogia das abelhas os exemplos são vários onde que eu gosto bastante É sobre o crescimento das sementes dos Girassóis Se você olhar bem vai perceber que elas crescem formando espirais nesse Girassol se nós contarmos o número de espirais formadas pelas sementes obtemos 34 que é um número de chocolate se contarmos
as espirais curvados na outra direção obtemos 21 outro número de Fibonacci Por falar em espirais os números de Fibonacci possuem uma representação geométrica que forma uma espiral bastante popular é o seguinte começamos com quadrado de tamanho um depois colocamos outro quadrado idêntico cima dele aí vamos lá os novos quadrados com lado igual a soma dos quadrados anteriores essa regra é a mesma da sequência de Fibonacci portanto os lados dos quadrados são exatamente os números de Fibonacci ligamos vértices desses quadrados Encontramos uma espiral essa espiral é um formato que ficou bastante popularizado por ser supostamente encontrado
na natureza na arte e na arquitetura a orelha humana os ossos do punho fechado a concha de um Nautilus construções clássicas a Monalisa acontece que todas essas representações são aproximadas e se você estiver com um pouco de tempo sobrando dá para sair por aí encaixam numa espiral de Fibonacci em praticamente qualquer coisa que você encontrar pela frente e portanto Essa obsessão de enxergar espiral de Fibonacci em tudo quanto é canto não é algo lá muito científico mas se tem uma coisa realmente científica relacionada a sequência de chocolate é o exemplo que deixamos para fazer agora
está relacionado com o nosso DNA vamos conversar com um homem ele tem um cromossomo x recebido da mãe e o cromossomo Y recebido do pai nós queremos rastrear os ancestrais desse cromossomo x do nosso homem contando Quantos anos tem passado os transmitiram esse cromossomo a cada geração até chegar nele o homem é origem do seu próprio cromossomo Portanto o primeiro termo é um na segunda geração a geração dos seus pais esse cromossomo herdado de sua mãe mas não seu pai como ele só aparece em um membro desta geração o segundo termo também é um a
mãe do homem receber um cromossomo x e sua própria mãe avó materna e um seu pai o avô materno o e portanto na terceira geração existem dois membros com aquele cromossomo x e o terceiro termo é dois e por aí vai a cada vez que temos um homem a geração de cima terá uma mulher com um cromossoma x a cada vez que temos uma mulher a geração de cima terá tanto homem como uma mulher com cromossomo x portanto como para cada pessoa numa geração existe uma mulher na geração de cima o número de ancestrais com
um cromossomo x o nosso homem original de uma certa geração é igual ao número de mulheres com esse cromossomo na geração de cima assim basta entendemos como se comporta as mulheres eu que deduzimos para elas Vai Valer a Pena total dos ancestrais é só dar uma geração sabemos que as mulheres numa geração são as mulheres da geração anterior somadas com os homens mas esses homens são e mesma quantidade que as mulheres de uma geração abaixo Portanto o número de mulheres em uma geração é a soma do número de mulh há duas gerações anteriores e essa
é a mesma relação de fibonattis logo o número de ancestrais que um cromossomo X em cada geração é dado exatamente pela sequência de Fibonacci como vimos os números de tribunais são interessantes tanto pelo lado abstrato e matemático como pelas suas surpreendentes aparições a natureza Eles são um verdadeiro prato cheio para mentes curiosas lembra que os números de Fibonacci correspondem ao número de espirais da semente de girassol Isso é apenas uma coincidência ou existe algo mais profundo por trás disso na verdade existe uma teoria que consegue explicar o porquê disso a chave deste mistério está no
número intimamente relacionada a sequência de Fibonacci o número de ouro Mas isso é um assunto para um outro vídeo se você curtiu esse vídeo deixe seu like se inscreve no canal e Ative o Sininho das notificações para continuar assistindo a mais conteúdos como esse e se você conhece alguém que possa se interessar por esse tipo de assunto compartilhe esse vídeo para que o nosso canal consiga chegar a mais pessoas o tem ciência é um canal iniciante e ainda muito pequena e a melhor forma de crescermos é através do boca-a-boca se você curtiu divulga para os
seus amigos nas suas redes sociais pode ser pelo Twitter pelo WhatsApp pelo Facebook pelo Instagram ou qualquer outro meio assim você contribuir demais para o nosso crescimento e ajuda esse vídeo ah não se perder rodopiando pelo YouTube dentro de uma espiral de Fibonacci foi um grande prazer fazer esse vídeo para você e até breve
Related Videos
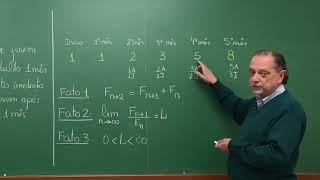
20:40
Sequência de Fibonacci
Professor Possani
84,752 views

9:00
Lo que nadie sabe de la sucesión de Fibona...
Derivando
425,046 views

12:27
IDENTIDADE de EULER: A Equação MAIS BONITA...
Tem Ciência
124,664 views

6:25
The magic of Fibonacci numbers | Arthur Be...
TED
5,656,023 views

16:21
MITO OU VERDADE? | Por que a SEQUÊNCIA DE ...
Blu Ciência
65,331 views

7:26
O que é a sequência de Fibonacci e por que...
BBC News Brasil
2,705,231 views

13:06
The MOST MYSTERIOUS NUMBER in the UNIVERSE
Ciência Todo Dia
1,909,802 views

10:02
O PROBLEMA (quase) IMPOSSÍVEL | Problema d...
Tem Ciência
244,744 views

8:22
EXEMPLOS NÃO SÃO DEMONSTRAÇÕES - Ledo Vaccaro
Principia Mathematica Cortes
1,589,763 views

7:24
Qué es la serie de Fibonacci y qué tiene q...
BBC News Mundo
1,628,374 views

16:02
EMMY NOETHER: A MAIOR Matemática da Histór...
Tem Ciência
79,000 views

23:39
A Razão Áurea e a ideia de beleza
Professor Possani
17,653 views

13:13
Número de Ouro, Phi, Sequência de Fibonacci
Angelle Hipolito Matemática
16,922 views
![The most beautiful equation in math, explained visually [Euler’s Formula]](https://img.youtube.com/vi/f8CXG7dS-D0/mqdefault.jpg)
26:57
The most beautiful equation in math, expla...
Welch Labs
825,681 views

1:04:58
Aula #01 - Como utilizar a Sequência de Fi...
Leo Becker
32,177 views

27:33
Donald no País da Matemágica e O Número de...
Nerdaus4.0
866 views

14:19
DE ONDE VEM O NÚMERO DE EULER (e) | Ledo V...
Cortes de Matemática e Física
364,301 views

13:59
A 2ª EQUAÇÃO MAIS BELA da Matemática
Tem Ciência
58,313 views

24:53
A Beleza da SEQUÊNCIA FIBONACCI na Biologi...
Matemática Rio com Prof. Rafael Procopio
7,352 views

12:58
O PROBLEMA DE BASILEIA: o motivo que torno...
Tem Ciência
18,545 views