Simple Examples of PID Control

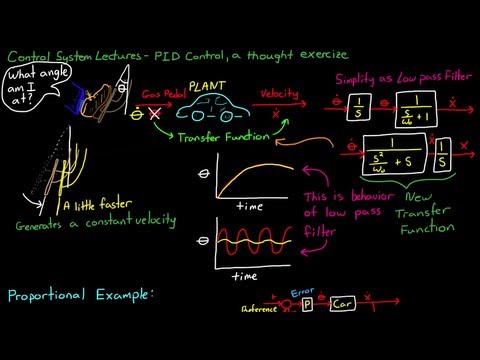
welcome back to control system lectures in this video I'm going to continue discussing PID controllers by walking you through a thought exercise that's commonly used to explain PID control during this example we'll try to use reason and logic rather than math to see how PID controllers and their variations are used to generate the desired system response for this example you're driving your car which is the plant and you use the gas pedal to control the velocity of the car we'll call the angle of the gas pedal Theta where the angle of zero is when your

foot isn't pressing on the pedal now I want to create a real simple model of the car to work off of so that if you want to verify our results of this exercise on your own you can we need a transfer function from the gas pedal position to the velocity of the car now in real life this is a complicated nonlinear transfer function that's dependent on the car model however you can simplify this model by assuming it's just a first order low pass filter and the transfer function for a low pass filter looks like this

where the output is velocity and the input is angle so let me explain why this is a reasonable estimate if you press the gas pedal down halfway the car would start to accelerate and then eventually settle at some constant speed and stay there and I can say that any position of the gas pedal if you held it there long enough would result in a constant velocity that corresponds to that pedal position and if you press to down just a little bit more then that speed would increase a little bit faster but here's where the low

pass filter comes in if you press the gas pedal down slowly which is the red line then the car will be able to change its velocity according to the pedal position the yellow line but imagine if while you were driving you started pumping the gas pedal all the way down to the floor and back up the car wouldn't have enough time to respond to that and the velocity would stay relatively constant therefore low frequency inputs are passed to the output whereas higher frequency inputs produce an output that is much smaller and this is the signature

of a low pass filter but our model isn't complete at this point because no one Drives By knowingly putting the gas pedal at a specific angle you don't think to yourself I need to go 20 mph so I'll put the pedal at 10° instead people drive by applying a change in pedal angle for example you realize you're driving a little slow so you change the angle of the gas pedal by pressing it down a little bit more so our Command is actually change an angle over time which can then be integrated to produce an angle

which is the input into our low pass filter so the transfer function from the change in the gas pedal angle to the velocity of the car is then combined and would look something like this so keep this model in mind as we go through the exercises in this first example we're going to go over proportional control the closed loop control system for our car with a proportional controller would look something like this where the error is the difference between our reference command and the measured signal and the error is fed into our proportional controller now

imagine that you're sitting in your car stopped at a stop light and the speed limit for the road that you're on is 25 mph the light turns green and you begin to press on the gas pedal to accelerate up to the speed limit now in real life as you drive your car to respond to this step command you're unknowingly performing proportional control here's what happens initially you're commanding 0 mil per hour and once the light turns green your reference signal steps up to 25 mph at this point you have an error of 25 mph and

this is a large error so you apply a large change in the gas pedal proportional to that error and you press the pedal fairly fast because of that now as your velocity increases towards 25 mph your error gradually gets smaller and smaller so you gradually slow the rate at which you press the gas pedal and eventually the car reaches 25 mph and since the error is zero you stop adjusting the pedal and you hold it constant now at this point we can reason that with proportional controllers the steady state error will be zero so with

that in mind try to imagine what would happen if the gain was too large in this example now initially the vehicle is at rest and then the light turns green and there's a step up to 25 mph same as before and this is a large error and instead of pressing on the gas pedal slightly you floor it because of the high gain and before you have time to register that you've pressed the gas pedal too far your car is all the way up to 50 mph now at this point the error is now minus 25

milph so you slam on the brakes and again before you have time to realize your speed the car has stopped and then the cycle starts all over again and by increasing the gain you run the risk of making your control system unstable perhaps you or someone you know already drives like this where they apply too much gas or too much break all the time if that's the case then you can tell them that maybe their gain is a little bit too high okay so let's look at another example now this time let's add the derivative

term to the control system but we'll change the problem just slightly it's the same start as before where you're sitting in a red light but now there's another stop light just down the Road that's also red in this example you're trying to control your position instead of speed so that when your light turns green your reference position which is where you want to be steps up from zero to the position of the next light in the block diagram this would equate to adding an integrator right here at the end to convert from velocity to position

and so now this is the new transfer function for the system in this example also your reference signal would change from speed to a position position since this is what you're trying to control so now let's apply a proportional controller to that and see what happens again your reference position would step up to the position of the second stoplight and since initially your error is large you apply a large proportional change in pedal angle the car begins to accelerate and as you get closer to the stoplight the error gets smaller and smaller and the magnitude

of the change of pedal also gets smaller eventually you arrive at the light and right when you're there the error goes to zero because you're at the position you want and you stop changing the angle of the pedal so everything's okay right wrong not only do you have all that acquired speed but you're still pressing the pedal down and you blow right past the light now once you pass the light the eror begins to grow negatively and you start releasing the pedal and eventually you put the car in reverse and start heading back to the

light but you have the same problem in that direction and you end up just oscillating back and forth so the next time you run a red light you can just tell the officer that you only ran it because you drive with a proportional controller and that's just what it does of course more than likely the officer will just say tell that to the judge and it's going to hand you the ticket anyway but you can avoid all of that mess by using a proportional derivative controller when you add the derivative term to the controller making

a PD controller you're adjusting the change in angle of the pedal based on on the rate of change of the error as well as the magnitude in other words you recognize that you're closing in awfully fast on the light so you'd better start releasing the gas pedal a bit early it works like this at the beginning you have lots of error and you aren't moving so the proportional path is large and the derivative path is zero once you start accelerating towards the second light the error gets smaller but is still positive so you continue to

press the pedal further but more slowly than you did before in addition you're starting to close in quickly on the second light so the time rate of change of the error is getting more negative the result is that the derivative path causes you to slow the change in pedal angle eventually the error is small enough that the proportional path contributes less than the derivative path and you start to slow the card down and this occurs earlier than your reference position and if you've tuned yourself properly which Loosely means that you know how to drive then

you're going to stop right at that second light now one way to think of the interaction between proportional and derivative is that the proportional path tries to get you to the destination as fast as possible while the derivative part is trying to restrain you from moving too quickly in this case it takes the balance of the two to properly stop at the light finally let's put the entire package together and look at PID control let me quickly rewrite the Clos Loop control system here so that we have a starting point for what I'm about to

say now remember at the beginning I said no one dro Drives By commanding an angle to the gas pedal rather they drive by commanding a change in the angle well in this example we'll command an angle and I'll show you why that's not a good idea and then I'll show you how PID control can help in that situation let's say you're in your car and you're trying to drive right beside your friend who's moving at a constant speed in this case the reference signal is the position of your friend if the output of the controller

is a pedal angle it's easy to see that there's going to be a steady state error and you will always trail behind your friend and never beside him imagine this you're some distance behind your friend and you're both going the same speed in that case you have an error signal that looks like this and since the error isn't changing over time remember that your speeds are matched the derivative path is zero and let's assume that the error in the proportional path causes you to press the gas pedal down to its current location in this situation

you're not going to move the pedal at all and you'll continue to drive behind your friend since your velocities will still be matched so now you might be thinking maybe your proportional gain isn't high enough if it was you could go a little bit faster and catch up to your friend if you increase the gain then the proportional path will cause you to press the gas pedal down to a new lower position and you'll drive a bit faster catching your friend however as you get closer the error gets smaller and so you begin to release

the pedal causing the car to slow back down again so so by increasing the gain all you've done is shorten the distance between you and your friend which is the steady state error but you haven't removed the error you can easily see the flaw in this thinking by assuming you start out at the exact speed and location as your friend and you use a PD controller in this case both the proportional and derivative error terms are zero so you immediately release the pedal and start slowing down so by controlling pedal position and using a proportional

derivative controller we we have no way of bringing the steady state error to zero now this is where the integral path comes in handy to remove steady state errors when you're trailing behind your friend and the error is constant the integral path will slowly build up error adding more and more pedal to the output it works like this the error starts out constant just like it was before and just like before you're holding the pedal exactly where it already is and you're trailing your friend but since the error term is non zero the integral path

is summing up that error over time and gradually increasing the pedal's position eventually as you close the gap with your friend the proportional term will be zero since there's no error you're exactly equal with your friend the derivative term will be non zero since you're closing the Gap with your friend but if you're closing slow enough it won't have much of an effect on the output but the important thing is that the integral term is going to be held constant at the exact pedal position that you need and this is how all three terms are

used to control a large variety of control problems and I use this car example to illustrate it because most people can relate to it and you can actually imagine the system reacting to different controllers but keep in mind that these examples are analogous to many systems in real life if you have a good understanding of the Dynamics in the system then it's possible to reason through the problem to determine what type of controller you need however choosing a controller is only part of the solution you now have to tune the controller in in order to

meet your system requirements and in these thought exercises we really only looked at one of those requirements and that is whether the error in the system eventually reached zero however in a real system you tune the controller for much more than that for example you might be concerned with overshoot or rise time or settling time and I'll cover how to tune PID controllers in future lectures and we'll touch on each of those requirements in more but for now I hope this gave you a little bit more intuition on how each of these three pads in

a PID controller contribute to the overall control system and as always thanks for watching