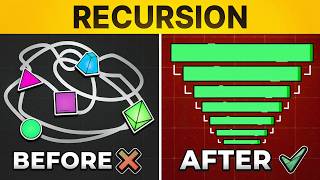
these are the eight most important patterns for coding interviews and this is backed by data these patterns are split into the two major categories of leak code problems linear which work with linear data structures like arrays linked lists and strings and nonlinear which work with nonlinear data structures like trees and graphs in this video we're not only going to learn these patterns but we're going to use pre-built code templates for these patterns that you can use for any leak code problem there are of course lesser use patterns we will not be addressing in this video
to see those as well as a lot more in-depth content explaining everything you need to know about leak code check out our website at algo monster all patterns for linear structures build off of two pointers which is why we're starting with it the two pointers pattern is important because it allows you to significantly reduce the time complexity of problems that involve traversing a linear structure like arrays linked lists or strings instead of the Brute Force approach where you might check every combination of elements which could lead to an O n^ squ time complexity two pointers
often allows you to solve these problems in linear time o n making it incredibly efficient there are two main methods of using two pointers the two pointers can go in the same direction or opposite directions and each are used for different kinds of problems when the pointers move in the same direction this technique is ideal for problems where you're processing or scanning the data in a single pass a common use case is the fast and slow pointer approach for detecting Cycles in length lists or for finding the middle of a list the slow pointer moves
one step at a time while the fast pointer moves two steps this allows you to efficiently check for Cycles or find key elements without ret trving the structure when the pointers move in opposite directions this is typically used in problems that involve finding pairs or comparing elements from opposite ends of the data structure a classic example of this is finding two numbers in a sorted array that sum up to a Target value one pointer starts at the beginning of the array and the other at the End by adjusting the pointers inward based on the sum
you can quickly zero in on the correct pair eliminating unnecessary comparisons the sliding window pattern is an extension of the two-pointer pattern but with a more focused purpose while two pointers involves using two separate pointers to Traverse and manipulate a data structure sliding window refines this by maintaining a window of elements within the data dynamically adjusting its size as you progress through the structure essentially you're using two pointers but the goal is to manage a range or subset of elements that satisfy a specific condition like a subarray or substring in the sliding window approach one
pointer marks the start of the window and the other marks the end as the endp pointer advances the window slides over the data structure depending on the problem you either expand the window by moving the end pointer or contract it by moving the start pointer to meet certain criteria like maximizing the length of a substring or maintaining a sum within a Target value for example in a problem where you need to find the longest substring without repeating characters the window expands by moving the end pointer to include new characters if the window encounters a repeated
character the start pointer moves forward to shrink the window and eliminate the duplicate this Dynamic process allows you to efficiently solve problems that require analyzing continuous segments of an array or string without ret trving the structure multiple times sliding window is extremely powerful for problems that require tracking contiguous sequences whether it's for Strings subay or link lists it adds more versatility to the two-pointers pattern by giving you control over a range of elements at any given point and it's often combined with hashmaps to keep track of the elements within the window for a deeper dive
into common problems solved with sliding window check out algo dooner binary search is a fundamental search algorithm that allows you to find a Target value in a sorted array by repeatedly dividing the list in half it is also technically an expansion of the two pointers pattern because it uses a left and right pointer that have the list step by step binary search starts by looking at the middle element and checking if that's the target if it is the target success you can return it if it's smaller than the target you know the target is somewhere
to the right so we repeat this process but only on the right half if it's larger than the target we repeat the process on the left eventually we Converge on the target this is an efficient algorithm because it allows us to find our Target in logarithmic time ol log n rather than searching each element which is o n however binary search is far more applicable than only being used on sorted numerical lists what makes binary search incredibly powerful is it can be used on any list where there is a monotonic function a monotonic function is
any type of pattern where there is a consistent increase or decrease which extends Beyond just numbers put more simply we are looking for any type of condition that can be used for sorting not just strictly increasing numbers for example if we had a sorted list of only true and false we can actually use binary search to find the first true occurrence the binary search would work like this you look at the middle of the list if the middle value is true you know that the first true must either be here or somewhere to the left
so you move your search to the left half if the middle value is false you know that the first true must be to the right so you focus on the right half this type of searching based on where a condition is true and where it is false can be reused for every single binary search problem in fact we actually have this free template for this on our website Alam monster all we need to do is find out what makes something feasible for example the common leak code problem minimum in rotated sorted array doesn't appear to
follow binary search at first after all it's not sorted however there's a monotonic condition we can use to apply binary search the condition is that any element that is less than the last element of the array is part of the rotated section while any element greater than the last element is part of the original sorted section we can mentally convert this to trues and falses and just like that we have the same true and false question we just solve this can be applied to a ton of different questions for more practice and an in-depth explanation
check out algo dooner now we'll take a look at nonlinear structure problems which work with trees and graphs in fact instead of treating trees and graphs as two entirely different structures you should imagine that a tree is just a graph with no Cycles the only difference between the two is that for a graph that could have Cycles you need some visited set to keep track of nodes you've already visited this makes the patterns we will talk about applicable to both for nonlinear problems we'll start with breath first search as it's the easiest algorithm to understand
and build off of breath first search is an algorithm used to explore nodes in a graph or tree level by level the idea behind this is that it starts at a given node commonly called the root and explores all its immediate neighbors first before moving on to the neighbors neighbors and so on to keep track of the nodes that have already been visited so that we don't revisit them BFS uses a que a data structure that works like a line first in first out this ensures that nodes are visited in the correct order starting from
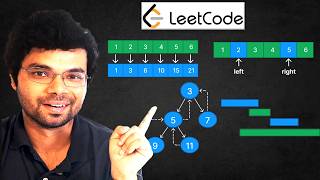
the closest to the route and moving outward BFS is such a common algorithm that you will use all the time luckily for you instead of having to derive it from scratch each time we have this template that we can reuse if you want to see more about how we got this template check it out at algo dooner now let's see BFS in action we're going to use this template to solve a common Le code problem level order traversal of a binary tree the problem asks us to give all of the levels of the tree at
each depth this means we need to visit the nodes of the tree level by level starting from the root and moving down visiting all the nodes at each level before proceeding to the next for examp for example given a tree with the root node three and children 9 and 20 where 20 has children 15 and 7 we need to return the values of the nodes level by level in the following order first 3 then 9 20 and finally 1516 for a solic kill we can solve this problem using BFS as it's ideal for level by
level traversal the idea is to use a q to help explore the tree one level at a time first we add the root node to the queue then for each level we process all nodes currently in the queue by removing them and adding their values to the result for each node we process we also add its left and right children to the queue so they can be processed in the next level this ensures that we visit all nodes on one level before moving to the next by repeating this process until the queue is empty we
can Traverse the entire tree level by level and collect the node values in the correct order finally we return the list of node values grouped by levels depth first search is an algorithm that builds on the foundation of BFS but explores the tree or graph in a different way while BFS focuses on exploring nodes level by level DFS Dives deep into one path as far as possible before exploring the next PATH in BFS we use a q to process nodes in a breath first manner ensuring all nodes at one level are explored before moving to
the next in contrast DFS uses a stack to explore nodes in a depth first manner where you keep going down one branch until you reach the end and then you come back to explore other branches most often the stack DFS uses is the call stack as most DFS implementations use recursion where BFS is ideal for finding the shortest path or exploring nodes layer by layer DFS is more suited for problems where you need to explore all paths or check every possible configuration such as finding all paths in a tree searching for a specific condition deep
in the structure or detecting Cycles the depth first nature of DFS makes it more memory efficient in some cases but it's less suited for problems where the shortest path or shallow exploration is required as it doesn't guarantee finding the closest solution first like with BFS DFS is a common algorithm that you will use all the time so we have a template that we can reuse again if you're curious to how this works check it out at algo dooner now let's solve a leak code problem with DFS a common leak code problem that uses this pattern
is called number of islands this problem asks us to count the number of islands in a 2d grid where one represents land and zero represents water an island is formed by connecting adjacent ones horizontally or vertically we need to determine how many distinct Islands Exist by identifying connected components of ones in the grid for example in a grid where someone's are grouped together each connected group is considered an island our goal is to Traverse the grid find all islands and count them we can solve this problem using DFS to explore each island the idea is
to iterate through each cell in the grid when we encounter a one land it indicates the start of an island from there we perform DFS to visit all connected ones all parts of the same island by exploring the neighboring cells in all four directions as deep as they go during the DFS we Mark each visited cell by changing its value to zero to ensure we don't count it again once all connected cells for that Island are visited we increment the island count and continue searching the rest of the grid this process ensures that we explore
each island once and count it correctly by the end the total number of initializing DFS calls we make not including the recursive calls equals the number of islands backtracking is a pattern that many people struggle with but in reality it's actually just an extension of depth first search in DFS we typically Traverse through a pre-built structure like a tree or graph where the nodes and connections are already defined with backtracking however you often have to build the solution tree yourself as you explore different options especially in combinatorial problems where the structure of the tree isn't
given explicitly but is generated dynamically as you make decisions in a backtracking problem you explore all possible solutions by making a series of decisions each decision represents a node in the tree and each potential decision forms a branch as you explore a decision you either reach a valid solution or you hit a dead end when a decision leads to a dead end you backtrack to the previous decision undo it and try another path just like with all of our other patterns we also have a template we are going to use here which is this now
let's walk through it by solving a leite code problem letter combinations of a phone number in this problem we're given a string of digits typically from 2 to 9 and we need to return all the possible letter combinations that the digits could represent using the mapping of a phone keypad for example if we have the digits 23 each digit corresponds to a set of letters two maps to a b c and three maps to d e f our goal is to generate every possible combination of these letters so for 23 some outputs could be a
d AE AF BD B BF and so on now our goal is to find all of these combinations backtracking is the optimal approach for solving this problem because it allows us to explore each possible letter one at a time while pruning invalid configurations early rather than brute forcing through every possible combination backtracking lets us build the solution letter by letter discarding incomplete paths that no longer make sense we start by taking the input digits and starts by checking if the input is empty returning an empty list if so it initializes an empty list a to
store the results and defines a recursive helper function DFS to perform depth first search DFS the DFS function tracks the current position in the digit string using start index and builds combinations step by step by adding letters to the path list if the start index reaches the length of the digits the current path is a complete combination so it's joined into a string and added to ANS for each digit the function iterates over its possible letters retrieved from a digit to char dictionary adds each letter to path and calls DFS recursively for the next digit
after exploring a letter it backtracks by removing the last letter from path to explore the next possibility the DFS starts at the first digit with DFS Z empty list and once all combinations are generated it Returns the result list ANS the overall time complexity is 04 to the power of n where n is the length of the input digits as each digit can map to up to four letters this approach efficiently explores all possible letter combinations and ensures that we backtrack after each combination is formed to explore the next one if you want to see
more problems solved with backtracking or a more in-depth explanation of the algorithm make sure to check out our website at algo dooner you may notice a lot of questions titled like the following anytime you see a question related to top k k smallest or k largest you always use a priority cu the the most common implementation of priority cues are called heaps heaps can be used to solve all of these questions a heap is a special type of tree where the elements are organized in a specific way there are two kinds of heaps in a
Min Heap the smallest value is always at the top aka the root and each parent is smaller than its children in a Max Heap the largest value is at the root and each parent is larger than its children one thing that is counterintuitive is that we use a Min Heap to find the K largest values and a Max Heap to find the K smallest values the reason is best explained with an example let's say we want to find the three smallest values in this list of seven we first create a Max heap of size three
we go through and add the first three values to it 3 6 and 1 to fill it out then once we hit the fourth value how do we know whether to add it or not well in a Max Heap the largest value is at the root and because we want the three smallest values all we need to know is whether or not this new value is smaller than our previous largest value in this case it is so we remove the value at the root and add our new value as you can see this is why
we use a Max Heap for finding the K smallest values and the vice versa for K largest values the reason heaps are efficient is because we always know where the largest or smallest value is at the root heaps allow for efficient access to the smallest or largest element in 01 time and inserting or removing elements takes ol log n time both of which are better than having to go through every element in a list lastly dynamic programming or DP is considered the hardest pattern to learn this is mostly because there are so many different variations
and nuances to the problems that fall under this category DP problems typically involve optimizing a solution by breaking it down into overlapping sub problems storing the results of these sub problems and reusing them to avoid redundant computations there are two major ways to do DP top down and bottom up in a top- down approach you start from the main problem and recursively solve its sub problems storing the results of those sub problems to avoid solving the same sub problem multiple times this may seem complicated but you actually already know how to do most of this
because top down is basically just backtracking with the added step of memorization memorization is just a fancy word for a simple concept concept it means saving the previous function call result in a dictionary and reading from it when we do the exact same call again in a bottomup approach you solve the smallest sub problems first and use their solutions to build up to the solution for the larger problem instead of relying on recursion bottomup dynamic programming typically involves filling out a table where each entry represents the solution to a smaller sub problem you start with
the base cases and iteratively compute the solutions to progressively larger sub problems until you reach the final solution this approach avoids the overhead of recursion and memorization often resulting in more efficient time and space usage bottom up is commonly used when you know the dependencies between sub problems and can structure the solution iteratively dynamic programming is far too complex to dive into in this video luckily we have a full section dedicated to it on our website at algo dooner as well as a free video dedicated to it both links are in the description