NMR Spectroscopy: Compound Multiplets and Splitting Trees

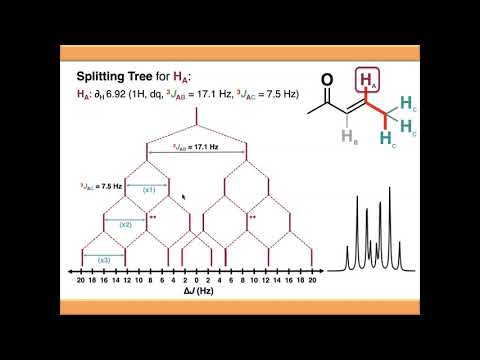
so this video is going to introduce compound multiplets and explain how we can use splitting trees to interpret the multiplicity of our signals so in the previous video we talked about what coupling was and what causes it and how we can categorize our signals into a number of different categories so either singlet where we don't have any coupling simple multiplet where we're coupling to one other chemical environment compound multiplets where we're coupling to more than one other chemical environment or complex multiplet where there's something else going on such as signal overlap so this video is going to focus on compound multiplets and the example i gave in the previous video was this proton here in purple which has two chemical environments one to either side of it so because these two chemical environments are different from each other when the red proton or the purple proton couples to these two environments um it will do so to form a compound multiplet so in a compound multiplet we basically treat it the same way as a simple multiplet it's just that we couple to each of the chemical environments in turn and each of these couplings could have a different j constant or it could have the same j constant but it would be coincidental if it did so starting out by looking at the coupling of proton a with proton b you would expect this to be a doublet um based on the n plus one rule as we saw previously and if you were to couple ha to hc you would expect that to be a triplet because there are two equivalent protons in that chemical environment so essentially all we do is to work out the final signal it's a combination of the couplings and the constituent j values so in this case we would end up with a doublet of triplets and that's what we can see in this signal down here this is the the nomenclature that you typically see in in research papers and that kind of thing so we discussed this in the previous video so the 3j a b coupling which is a three bond coupling between a and b and then the magnitude of the j value in hertz and the same for ac so one way that we can understand and interpret the multiplicity of our signals is using splitting trees so i'm going to show you how these work and we're going to start with the splitting tree for signal a so we can see that we've got our j values up here so we'll be able to insert these into the splitting tree and predict what the signal is going to look like so if we start out with our uncoupled signal for a now you'll notice that the x-axis down here is in delta j so this is measured in hertz and it's basically going to allow us to work out the magnitude of our or reflect the magnitude of our j values so notice it's not in chemical shifts so the chemical shift of this signal is given up here is 6. 82 so when you're seeing this signal on the actual nmr spectrum um the center of this uh this signal will be 6. 82 and then the magnitude of the j values obviously is given in hertz so what we're going to do is we're going to show the couplings to each of these three protons individually so i tend to start with the largest coupling and that's the one between a and b in this case but i'll show you later it doesn't really matter which you do first so starting out with the 3j ab coupling it's a 17.

1 hertz magnitude coupling so we show this splitting on the splitting tree like this now notice that you haven't gone 17. 1 hertz in one direction and 17. 1 hertz in the other you've gone half of 17.

1 in one direction and half of 17. 1 in the other so that the gap between the two signals is 17. 1 hertz now if protons c weren't here if the molecule stopped here or there was something blocking this position this is what your signal would look like because ha would just be coupling with hb it would give a simple multiplet in this case a doublet and you'd have a one-to-one doublet where the gap between the two peaks in the signal was 17.

1 hertz but hc does exist they are here so we're going to have to couple against those as well and whenever you've got multiple equivalent protons you couple against both of them individually that's just how splitting trees work so let's start with the first one the magnitude of the j value now is 7. 5 hertz so we need to take these two signals that we've just created and split them again by 7. 5 hertz this time so again go half of 7.

5 in one direction and half of 7. 5 in the other so that the gap between the signals is 7. 5 hertz so now what we need to do that's our first splitting we need to split again against the second one so we need to split all of these signals again by 7.

5 hertz and what you'll notice now is because we've split 7. 5 hertz here and 7. 5 hertz here this is our second coupling two of our signals have coalesced here and if you remember when we saw pascal's triangle on the previous video we add these signals together to get our signal intensity so we have a signal intensity of one over here and a single intensity of one here they've come together and coalesced so this signal here will have an intensity that's twice as high and i'm going to denote that just by using a double asterisk in this case and you'll notice that it's happened again over here so we'll denote that with a double asterisk so if we look at what our signal actually looks like we need to make these signals twice as intense so our final signal will look something like this on our actual nmr spectrum and if we look back at what it looks like we've got a one to two to one triplet and then a one to two to one triplet and they're split by the second j value which is that of the the doublet if you like but this is reflected in our splitting tree so our splitting trees allowed us to predict what our signal is going to look like just given the j values that we've got up here so the beauty of splitting trees is it doesn't matter which order you do the splittings in so i always tend to start with the the larger splittings and go down to the smallest because it makes your tree uh neater and sort of easier to interpret but it really doesn't matter which order you want to do them in so if we start with the couplings to hc this is the first one and then we need to split against the second one so this gives us a triplet at this stage so if hb wasn't here you know uh proton a would give us a triplet because it's coupling to these two equivalent protons c but hb is here so let's do the final coupling to hp and we split all of these signals by now by 17.

1 hertz uh remembering that any signals that are twice as intense need to be reflected in the final product so if we look at our final signal it looks exactly the same as what we had before and just to really prove a point um if we do the signals in a really weird order so we do one of our hcs then hb then the other hc then the signal that we end up with from our splitting tree is once again exactly the same so if we make the situation a bit more complex all i've done is shorten the molecule by one carbon so that hc is now an environment with three equivalent protons in it and you can see that the signal has got more complex and we're now starting to get into signals where you might look at them and go well you know i can't really interpret what that is so the splitting tree is going to allow us to work out what peaks have come from where and where our j values are in this signal so same principle as before let's start by coupling against hp that's again 17. 1 hertz gap i've kept all the j values the same for simplicity and we're then going to couple against three hc's so that's the first splitting then we've got the second splitting remembering that we're getting a signal that's twice as intense here now and then we're going to get a third splitting of these signals against the final hc now looking in this in this scenario here we've got a signal which is twice as intense meeting one that's um a single intensity if you like so this adds up to three so we've got all of these scenarios where a signal which is twice as intense as a meta standard signal if you like and we've got now signals which are three times as intense so if we look at what our signal looks like we've got this one to three to three to one quartet and a one to three to three to one quartet which is exactly what we've got in the signal over here and because we've constructed this using a splitting tree it becomes a little bit easier to see so you can see that um the area where the signals overlap here could get a bit confusing but you can see now there's evenly spaced gaps between these four signals which is one of the quartets and evenly space gaps between these four signals which is one of the other which is the second quarter now one of the scenarios that um splitting trees allow us to to clear up um is where we've got uh signals that should theoretically be something but look like something else um and that's where signals start to coalesce with one another or they overlap so if we take this simple example here um we're going to take uh hc which is the the power position of a of a phenol ring and we're going to see how it couples to hp so this is actually a simple multiplet so there is one j value here and as you'd expect hc gives you a triplet because you've got an hb on both sides so if we split against the first hp we've got a 7. 8 splitting and then if we split against the seven second um hb again we've got a seven point data splitting we meet in the middle to get a signal that's twice as intense so our overall signal is a one to two to one triplet and that is a simple multiplet so you can see splitting trees work exactly the same for simple multiplets no problems there so what happens if we move to this scenario now well you'll see in a lot of you know research articles and even textbooks and things like that um positions like hb described as being a triplet which if you're following the n plus one rule is technically correct there's two protons that it's coupling to but as i described at the beginning of the video these two environments are not the same right this is ortho to the amine group and this is para so these are not equivalent protons they're not in the same chemical environment so this is not a simple multiplet um what it is is a compound multiple but quite often what you'll see it described as and what the terminology that i tend to use is apparent triplet so this is a signal which looks like a triplet um and that's just because of the limitations of the spectrometer or coincidence but it's not really so if we look at the j values we've got b coupling to a is 7.

6 hertz b coupling to c is 7. 8 hertz so they're very very similar j values these could be identical but i'm going to show you what happens when they're just very similar so if we start by coupling to ha we've got 7. 6 hertz coupling here and then we're going to split everything again again by hc now because this j value is ever so slightly different these two signals don't quite coalesce in the middle if this was 7.

6 hertz they absolutely would and that would be it'd look like a normal triplet so you can see technically what we've got here is a doublet of doublets but these two signals in the middle are very very close together and what our signal actually looks like is a triplet so what i'm trying to say here is that technically speaking hb should give you a doublet of doublets but by pure coincidence or just the you know the situation that it's in the two j values that it's coupling to h a and h c with are very very similar they could even be identical so what you end up with is a signal that looks like a triplet because if you had a perfect spectrometer which had infinite resolution it would be able to tell these two signals apart and you would say clearly that's a doublet of doubles but we don't have a perfect spectrometer with infinite resolution so the spectrometer cannot tell these two signals apart so all you end up with is a coalesced signal in the middle which again looks like a triplet so this is an apparent triplet and all you're saying is i understand that hb shouldn't technically give me a triplet um but it looks like one and technically it's a doublet of doublets but you wouldn't report it that way you would say it's an apparent triplet so let's move on to a really complicated looking example now and let's see how we can reverse engineer a signal using splitting trees so this signal down here is the one for hp and you know if you look at it it looks fairly horrendous you wouldn't necessarily be able to tell me off the top of your head what that signal is but let's have a look at it on the on the scale if you like so what we're going to look for in this signal is any kind of repeat patterns and anywhere that there is a repeat unit of something now if you look down the zero the axis if you like you can see that the signal is symmetrical on both sides so everything on this side of the signal is reflected in everything on this side of the signal and that's usually a good sign that your signal is going to be interpretable in this way so the first thing that i've noticed when looking at this signal is that there's kind of a triplet pattern here and if you start to measure the j values between these signals if you can find any j-values that are repeated it's usually a good sign that they're actually a legitimate j value rather than just a coincidental gap between two signals now because the signal is symmetrical this triplet pattern over here is reflected um in this this side of the of the signal so if we look at hb obviously we've got the two equivalent ha protons so this is a good indication that this is probably the triplet that's coming from ha in the middle it gets a little bit more complicated um because we've got these signals these two signals here which look a little bit oddly shaped they're a bit um bit broad so we've extrapolated one of our coupling constants we know we're looking for something with 6. 2 hertz we think um but if we look in the middle of this signal then we can trace the same triplet pattern with the same 6. 2 hertz gaps into these signals here and assuming that these two are overlaid then that would explain why they look a bit strange so what we're going to do next is start to look for some of the other j values because obviously we're expecting we've got a 6.

2 hertz triplet coupling to ha but we're also going to have to look for a doublet coupling to hc and a doublet coupling to hd so if we start measuring the gaps between the triplets so i'm measuring the gap here between the left peak of this purple triplet and the left peak of this green triplet and this is 10 hertz exactly um if we start to measure again symmetrically on the other side right the rightmost signal of this red triplet and the rightmost signal of this orange one that gap is also 10 hertz so the fact that it's reflected and there's a consistent j value there tends to suggest it's probably a legitimate one so we're looking for a 10 hertz doublet coupling as well now if we measure the gap between the leftmost signal of the purple triplet and the leftmost signal of the orange triplet that gives us a gap of 16. 8 hertz and once again you can do this with any of the other signals and it should be reflected in all of them so that gives us another of our j values so remember when you're looking at these things the gap between the adjacent peaks in this case um gives us that triplet um j value but we're looking at the the consistent peaks in all of these patterns so the left you're measuring from the left signal of this triplet to the left signal of that triplet and so on so you wouldn't measure from the left signal of this triplet to the right signal of that triplet that's that's not a legitimate j value that's just nonsense so if we reverse engineer this and we go back into our splitting trig we're going to take our three j values and we're going to convert them into our splitting tree so i'm going to start with the biggest one 3jb to c which is 16. 8 hertz and then 10 hertz and 6.

2 and if we do the splittings as we've seen previously so we split the singlet by 16. 8 hertz to give us a doublet that's got a j value of 16. 8 if we then go against hd and split those two signals we've now got a doublet of doublets which is 16.

8 and 10 hertz and finally if we split against ha again do them one at a time so against the first one and then against the second one remembering to add up all of our coalescing peaks so these are twice as intense we end up with something that looks a bit complex down here but actually if we look at the the signal um it looks reasonably similar to what we've got over here the only bit that differs is the bit in the middle where we've got these two signals but as we saw in the previous example uh that's a limitation of the spectrometer it just can't resolve lines that are this close together so if we overlay our signal on top of our splitting tree actually it predicts perfectly what our signal looks like it's just that these signals in the middle are these two lines coalesced into one another so the other way that we can work out some of the j values that are in the signal for hb because i appreciate looking at hb on its own is quite challenging unless you know what you're looking for bear in mind that hb is coupling to h's a c and d and whenever a proton couples with another proton in a different chemical environment the j values in both of those signals are identical so we can look at the other signals for hc hd and ha and we can try and extract some j values from them so if we look at the signal for hc um these two kind of multiplets here are 16. 8 hertz apart again measuring from the leftmost peak of one to the leftmost peak of the other so that backs up what we found in this signal right that's the j value that we found in this signal just reflected in the signal for hc similarly if we do hd these two signals are now 10 hertz apart and again that's reflected in the signal that we've the the gap that we found in the signal for hp and finally if we look at the signal for ha the gap between these two is 6.