COTANGENTE, SECANTE E COSSECANTE (C/ EXEMPLOS) (AULA 11/24)
607.8k views1492 WordsCopy TextShare

Equaciona Com Paulo Pereira
Neste vídeo, eu trabalho com as razões trigonométricas COTANGENTE, SECANTE E COSSECANTE. Mostrando s...
Video Transcript:
Fala galera seja bem-vindo ao equaç eu sou o professor Paulo Pereira e vamos dar continuidade ao curso de trigonometria na circunferência falando hoje de cotangente secante e cosecante vem pro quadro comigo senhores bom para determinar as cotangent a gente precisa traçar este eixo aqui tá vendo que tangencia a circunferência Então esse eixo que é paralelo ao eixo X tá vendo é o eixo da escota tangentes E aí quando você tem um ângulo Alfa um arco de comprimento Alfa aqui tá vendo o que que vai ser então a cotangente dele pessoal muito tranquilo você pega a
reta que passa aqui pela origem pelo centro da circunferência trigonométrica e passa também pela extremidade do arco onde essa reta cruzar lá o eixo das cotang pronto esse valor ali então vai ser a cotangente do teu ângulo no caso ficamos com essa medida aqui ó Então esse tamanhozinho aqui já que tá na porção positiva vai ser a cotangente de Alfa beleza muito tranquilo pessoal bom o que é que você de fato precisa saber a propriedade que a cotangente tem não É difícil fazer você pode utilizar semelhança de triângulos aqui e você determina que cotangente de
X vai ser dado por cosseno x sobre seno x Tá certo propriedade importante e você já percebeu que é justamente o inverso da tangente lembra a gente viu aqui a tangente é a razão do seno pelo cosseno ficou inverso disso então a gente também pode escrever que cotangente é o inverso da tangente ou seja 1 sobre a tangente de E aí nos exercícios você escolhe qual utilizar qual ficar mais fácil para você beleza muito bem senhores vamos falar de secante e cossecante Então temos aqui a circunferência trigonométrica e um ângulo Alfa marcado tá vendo aqui
a extremidade do arco Beleza o que é que você faz nessa ocasião você pega atenção uma tangente à circunferência passando aqui pela extremidade vamos ter essa retinha aqui ó tangenciando tá vendo Beleza então onde cruzar aqui no eixo X você vai ter a secante do ângulo certo então no caso vai ficar sendo essa medida aqui ó Eis Aqui a secante assim que a gente escreve abreviado do ângulo alfa e lá no eixo Y onde cruzar você tem então então a cosecante do ângulo vai ficar sendo na ocasião esse essa medida aqui ó cossecante e não
vai dar para escrever não pera aí pera aí para não fazer muita bagunça vocês sabem né me con sabe que eu tenho toque de quadro inclusive vou ter que reforçar o vermelho ali Cadê rapidinho gente pronto eis ali então essa medida é a cossecante do ângulo Alfa só isso muito tranquilo e pros exercícios que é que de fato você precisa guardar as propriedades que a gente tem aqui secante é o inverso do Cosseno ou seja 1 sobre o cosseno e cossecante é o inverso do seno 1 sobre o seno Cuidado isso pode confundir porque você
né inicia aqui por se você pode associar o seno mas não secante é um sobre cosseno beleza e aqui iniciando por C aí você de repente associa o cosseno mas não tá cosecante é o inverso do seno 1 sobre seno beleza não sai daí deixa eu te mostrar uns exercício zinhos que você utiliza isso é rapidão tempo de apagar o quadro quadro apagado Vamos trabalhar alguns exercícios vem pro quadro bom aqui ele pede para você calcular tá a cotangente de 60 mais secante de 45 sobre 2 menos a cosecante de 90º bom você pode fazer
assim ó faz separado cada um deles quer ver você pode por exemplo pegar deixa eu trocar a caneta a cotangente de 60º vamos fazer aqui ó cotangente de 60º e calcular separado depois a gente junta tudo e faz a conta bom cotangente por exemplo é 1 sobre a gente acabamos de ver isso né eu optei por isso mas poderia escrever como cosseno sobre seno também vou fazer direto isso porque a tangente de 60 a gente conhece da tabela dos Arcos notáveis a tangente de 60 é3 tá isso você tem obrigação de saber pessoal não tem
jeito nesse momento a gente pode racionalizar que é multiplicar em cima embaixo por √3 vamos com 1 x √3 é √3 e √3 X √3 é √9 que é 3 pronto deixa quieto aqui vamos calcular aqui agora a secante de 45º formazin da secante é 1 sobre o cosseno ou seja 1 sobre o cosseno de 45º é o que eu vou ter aqui beleza que eu tenho obrigação de saber que que é o cosseno de 45 pessoal √2 so 2 nesse momento eu lembro da divisão de frações que eu devo conservar a primeira e multiplicar
pelo inverso da segunda então ficou 2 so √2 bom 1 x 2 É 2 e repito √2 embaixo Mas eu vou racionalizar também ou seja eu vou pegar o 2 sobre √2 e multiplicar em cima e embaixo por √2 a gente deve racionalizar isso tá bom olha que interessante que vai acontecer vai ficar 2 √2 sobre √2 x √2 que é √4 que é 2 Olha lá deu √2 fez aí o valor de secante de 45 por último eu faço aqui a cosecante de 90 vamos fazer aqui ó fulaz da cossecante né é um sobre
o seno Então eu tenho 1 sobre o seno de 90º seno de 90 é um arco de eixo 90º é 1 né Você também precisa saber isso já foi estudado aqui no canal sen 91 1 divido por 1 Claro é 1 daí a gente volta para cá e substitui tudo né A cotangente de 60º é √3 so 3 Então vou escrever aqui √3 so 3 mais valor de secante de 45º que é √2 sobre 2 menos o valor da cosecante de 90 is aqui ó 1 que a gente acabou de achar embaixo vai ficar um
né 2 - 1 é 1 Então vai sumir esse denominador vamos ficar só com isso aqui √3 so 3 + √2 que caso você queira converter isso para uma fração só é só você fazer assim ó 3 x √2 você multiplica aqui deixa eu repetir o primeiro aqui fica 3 x √2 e você repete o trê embaixo pronto beleza tranquilo dá um pouco de trabalho mas não é difícil fazer só você lembrar das formulas de cotangente secante vamos para exercício dois aqui que é um exercício clássico cai muito que é você simplificar expressões trigonométricas tá
só substituir as fórmulas por exemplo cosecante de X você sabe que é 1 sobre o seno secante de x é 1 sobre o cosseno Beleza ainda tem a parte de baixo que tem a cotangente que que é contente bom aí você pode usar tangente um sobre a tangente ou pode usar cosseno sobre seno tá um dos dois vai acabar sendo melhor na ocasião aqui eu vou utilizar agora a mais deixa eu só jogar isso um pouquinho para cima cadê o apagador tá aqui daqui a pouco eu fico sem espaço aqui repetindo he multiplica em Cruz
cosseno x x 1 cosseno x + seno x x 1 seno x e o denominador fica sendo produto esse vezes esse tá eu tô tirando a c né convertendo para uma fração só mas de uma maneira maceteada é só isso que eu tô fazendo tá embaixo vou fazer a mesma coisa ó multiplica e soma aqui também no macetinho pra gente nem pensar em MMC sen x x 1 é sen x no entanto você mantém o seno x como denominador beleza faz com calma você vai conseguir chegar nisso tá tirando Mc e tal é muito tranquilo
pessoal aí aparece uma divisão de frações você conserva a primeira deixa eu repetia aqui seno x ó tá vendo tô repetindo a primeira e Multiplica pelo inverso da segunda então vou inverter essa fração o seno fica em cima e o cosseno x mais seno x fica embaixo aí Acontece uma coisa interessantíssima né como eu tô eu tenho aqui uma multiplicação aqui aparece um termo que aparece embaixo também bem então vem aqui ó comigo ó cortou tá vendo isso dividido por Esso morreu dá um e ainda tem o seno ó vou cortar esse seno com esse
seno pode fazer isso pode tranquilamente porque você tá multiplicando aqui tá bom beleza sobrou só o quê gente sobrou só o cosseno emb baixo então em cima a gente coloca o um né ficou 1 sobre o cosseno de x que inclusive um sobre cosseno é a secante então aquele trem todo aqui no fundo ficou igual a secante de X beleza é isso espero que vocês tenham gostado sobretudo entendido se isso aconteceu deixe o teu curtiu para mim aqui se inscreve no canal pessoal tau Tchau Um abração [Música]
Related Videos

7:30
RELAÇÕES DECORRENTES DA RELAÇÃO FUNDAMENTA...
Equaciona Com Paulo Pereira
173,471 views

22:34
As 6 funções trigonométricas vistas na cir...
Professor Possani
95,299 views

6:41
Secante, cossecante e cotangente - Simplif...
Matemática no Papel
65,056 views

7:04
DEMONSTRAÇÃO DAS RELAÇÕES TRIGONOMÉTRICAS ...
Matemática Já
1,701 views

13:23
TRIGONOMETRIA | CÍRCULO TRIGONOMÉTRICO SEN...
Dicasdemat Sandro Curió
1,568,304 views

14:53
ARCOS: MEDIDAS E COMPRIMENTO - GRAU E RADI...
Equaciona Com Paulo Pereira
1,149,183 views

12:44
TANGENTE NA CIRCUNFERÊNCIA TRIGONOMÉTRICA ...
Equaciona Com Paulo Pereira
381,932 views

28:57
RELAÇÃO FUNDAMENTAL DA TRIGONOMETRIA - DEM...
Gis com Giz Matemática
177,990 views

9:56
A FUNÇÃO SENO (GRÁFICO, DOMÍNIO, IMAGEM, P...
Equaciona Com Paulo Pereira
1,389,767 views

16:41
Гипотеза Римана - Numberphile на русском.
Tomato Scientist
63,985 views

17:00
QUAL É A ALTURA DO PRÉDIO ?
MATEMÁTICA FOR ALL LUIS CARLOS
424,657 views

18:18
COTANGENTE, SECANTE E COSSECANTE 🚨 Aula c...
Prof. MURAKAMI - MATEMÁTICA RAPIDOLA
8,466 views
8:19
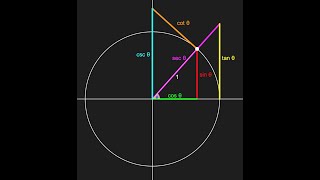
All 6 Trig Functions on the Unit Circle
Beautiful Math
1,390,752 views

6:33
RAZÕES TRIGONOMÉTRICAS - ALTURA DO PRÉDIO ...
Professora Angela Matemática
329,007 views

35:33
CÍRCULO TRIGONOMÉTRICO -
Gis com Giz Matemática
278,267 views

8:08
RELAÇÃO ENTRE TANGENTE, SENO E COSSENO (DE...
Equaciona Com Paulo Pereira
271,162 views

9:52
TRIGONOMETRIA 🚨 Como calcular SENO de 120...
Prof. MURAKAMI - MATEMÁTICA RAPIDOLA
20,467 views

10:07
RELAÇÕES TRIGONOMÉTRICAS FUNDAMENTAIS (DEM...
Matemática Já
3,309 views

3:40
TRIGONOMETRIA - (SENO) - Razões Trigonomét...
Professora Angela Matemática
247,337 views