Compensadores: Avanço, Atraso e Avanço Atraso (ELT009, ELT035)

o assunto neste vídeo será apresentar os compensadores em atraso e avanço de fase e a combinação de ambos que chamamos do compensador em avanço e atraso de fase uma das primeiras pessoas a tratar do projeto e desses compensadores foi este senhor que aparece aqui à esquerda de nome Albert Hall ele defendeu sua tese de doutorado em 1943 no MIT e o título da tese está aqui e nessa tese entre outras coisas ele por exemplo definiu círculos de MN que aparecem posteriormente na carta de nichols tanto é que nos no início da história os círculos m

n muitas vezes eram chamados círculos de Hall então eles pela primeira vez tratou desses círculos só que no plano S então eram círculos mesmo e ele também deu nome de compensador de avanço de fase de atraso de fase H compensadores que já eram utilizados a época mas ainda sem esses nomes além de dar o nome para eles ele definiu uma maneira de fazer o projeto né e basicamente algumas dessas técnicas a gente eh já tratou né em estes vídeos que aparecem aqui nesses vídeos tratamos do projeto dos compensadores pelo método do lugar das raízes veremos

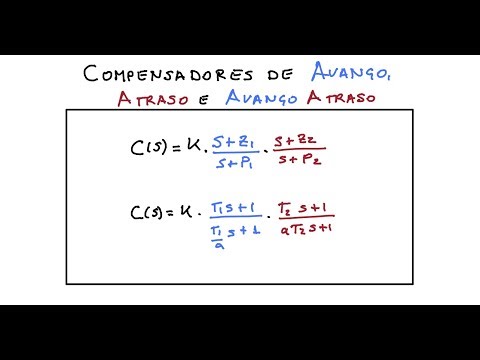
também mais no futuro o projeto dos mesmos compensadores no domínio de frequência muito bem o objetivo Neste vídeo é simplesmente apresentar estes eh essas estruturas de controle chamada compensadores e na sequência do curso ela esse vídeo deve ser assistido antes obviamente dos vídeos que tratam do seu projeto muito bem então basicamente o que faremos agora é uma uma descrição simples e das definições e apresentação desses compensadores eu vou mudar de cor aqui não enjoar vocês com preto Ok então começamos com o compensador de avanço de fase ele pode ser escrito desta maneira uma função de

transferência com uma KC um zer um polo sendo que o zero é menor que o Polo então no plano s no plano complexo representamos o zero e um polo dessa maneira Ok então o zero tá aqui né esse aqui é - Z e aqui aparece o polo em - P Observe que Z menor do que P significa que o zero está mais próximo à origem do que o Polo se tomarmos um ponto Qualquer aqui de teste e conectarmos encontraremos que o zero contribui com uma fase teta 1 o Polo contribui com a fase F1 e

teta 1 é maior do que F1 e como a fase do todo é teta - phi vemos que o resultado disso é uma fase positiva é um avanço na fase por isso que chama de avanço de fase pois bem uma maneira importante também de vermos esse compensador será no domínio de frequência representação utilizando o diagrama de Bod por exemplo Nesse contexto ao invés de escrever o compensador Desta maneira é comum escrever o compensador desta maneira obviamente são perfeitamente equivalentes a as formas de representar muito bem Então temos um zero e um polo né relacionados entre

si amarrados a sua distância amarrada por esse coeficiente a esse parâmetro a é um parâmetro positivo entre 0 e 1 e aparece aqui é o uma constante k Então vamos desenhar rapidamente esboçar o diagrama de bde muito bem o diagrama de bde Começa como é um sistema tipo zero ele começa com algum uma constante aqui e eu vou fazer isso aqui mais embaixo para não ficar apertado né então nós começaremos num valor aqui e observe que o zero está mais próximo da origem significa que o zero é de mais baixa frequência que o Polo portanto

aqui como esseo é frequência nós vamos encontrar com zero antes do Polo então encontramos com zero sobe o módulo sobe 20 DB por década e quando ele encontrar a frequência do Polo ele volta a estabilizar desse jeito assim ok muito bem eh que valor de ganho é esse esse é o valor de ganho CC então para fazer isso podemos tomar essa expressão e calcular o c na frequência zero faça S = 0 isso aqui é k portanto esse valor é 20 log na base 10 de k e Qual é esse valor aqui assíntota de alta

frequências para assíntotas de altas frequências teríamos que fazer Ômega tendendo a infinito fazendo o Omega tender a infinito Lembrando que S = Sigma + ega Então significa que teremos 1 ô aqui também ega então infinito sobre infinito fica indeterminado vamos aplicar lopital então aplicando o lopital derivamos em cima e embaixo no caso aqui por s em cima fica T embaixo fica a t os três cancelam isso aqui fica k sobre a Então esse valor aqui é 20 log na base 10 de k sobre a como a é menor do que 1 esse nível é superior

a esse de cá muito bem temos da fase e então começamos com fase nula como o zero aparece primeiro a fase aumenta depois aparece o Polo a fase diminui e volta para cá né obviamente isso aqui nunca chegará a 90 não tem como só chegaria a 90 por exemplo se nós não tivéssemos o Polo então isso aqui subiria e assintoticamente convergiria para 90 ele chega a uma fase máxima né que podemos indicar por Fi m e claro vai depender da posição relativa do Polo e do zero quanto mais próximos um estiver do outro tanto menos

tempo você tem para subir e ganhar fase Mas a distância entre o zero e o Polo ele são determinados nesse caso por um único parâmetro que é o parâmetro a portanto esse FM realmente ele só depende e do parâmetro a e essa expressão que envolve o seno é uma expressão útil pra gente entender né qual que é é a fase máxima que se ganha essa fase máxima ela ocorre na frequência correspondente ao omm que é dada por essa expressão e o ganho do compensador nessa frequência então se eu fizemos aqui nessa frequência omm o ganho

ele é dado por essa expressão aqui portanto esse valor aqui é 20 log na base 10 de k sobre ra a essas expressões serão utilizadas no futuro no contexto de projeto então vocês não precisam preocupar em memorizar ou guardar isso mas aqui já estamos Eh mais ou menos preparando o cenário Para o Futuro aqui temos o compensador de atraso de fase no caso do lugar das raízes a expressão é igual anterior a diferença agora é que quem é menor aqui é o Polo Portanto o Polo aparece aqui o zero depois então aqui - p aqui

- e se tomarmos um ponto teste qualquer sobre o eixo J Ô e ligarmos esses pontos o Polo contribui com fi1 o zer contribui com teta 1 a contribuição de fase desse sistema nesse ponto ou seja a resposta em frequência disso daqui né para a frequência correspondente a esse ponto a sua fase é teta 1 - F1 como o F1 é maior né a fase é negativa então e há um atraso na fase isso dá o nome para esse compensador no domínio de frequência nós costumar expressar esse compensador por atrás de fase dessa maneira Observe

que é igual a anterior a diferença agora é que a é maior do que 1 a maior do que 1 significa que essa constante de tempo relacionada ao Polo é maior do que a constante de tempo relacionada ao zero ou seja o Polo é mais lento que o zero é o que vemos exatamente aqui o Polo está mais próximo né da origem do plano S que é são as baixas frequências pois bem então isso significa que e começaremos aqui determinado valor o sistema tipo zero Primeiro vamos encontrar o Polo o Polo aparece em frequência mais

baixa e vai cair Men 20db por década quando encontrar a frequência do zero ele estabiliza aqui para encontrarmos esses níveis faremos como fizemos antes então C de 0 é igual a k então isso aqui é 20 log na base 10 de k e se Infinito ou seja a assíntota para frequência infinita derivando em cima e embaixo com respeito a s e depois fazendo S igual e a Ômega Então temos T sobre at Portanto o mesmo resultado de antes só que como a agora é maior do que 1 k sobre a é menor do que k

então aqui em DB temos 20 log na base 10 de k sobre a em termos de fase a fase começa em zero primeiro encontra o Polo reduz a fase depois encontra o zero aumenta a fase Lembrando que no caso da fase os efeitos do Polo do zero começam a ser sentidos uma década antes da frequência do pólito zero então de novo vemos que aqui a fase agora reduz com respeito eh a ou ou seja com respeito a à linha de zero então há uma redução de fase isso chama-se um atraso de fase ao contrário do

compensador de avanço aqui nós não temos as outras relações que existiam para o caso do avanço de fase e por fim temos a combinação dos dois né então a combinação dos dois temos eh essa parcela aqui agora eu distingui Z P1 de Z2 e P2 a relação entre eles é igual ou seja aqui Z1 é menor que P1 aqui Z2 maior do que P2 mas aqui o importante é observar que esses conjuntos esses serão de valor menor do que esses ou seja Z1 e P1 aparecem por exemplo aqui então Z1 P1 e aqui teremos P2

Z2 essa parte se encarrega do atraso de fase Essa parte é a parte do avanço de fase no caso da representação em domínio de frequência aqui as expressões são um pouquinho diferentes continuamos com uma constante k t1s mais 1 como antes agora em vez de a t1s Vamos colocar T1 sobre a s + 1 porque aqui a terá que ser maior do que um e essa parte continua igual então do ponto de vista de do desenho então e não é muito diferente então a parte de baixa frequência Observe que a constante de tempo relacionada a

esse zero Ela é maior do que a constante de tempo relacionado a esse zero ou seja isso aqui realmente é a parte de atraso a parte mais lenta vou colocar assim lento isso aqui é mais rápido então essa parte aparece primeiro isso aqui era para ser reto então assim acho os Polo encontro o zero e agora vamos encontrar o zero do outro e o Polo do outro e no caso da fase é alguma coisa que faz algo assim né do jeito que aqui foi definido utilizando a é o mesmo a aqui e aqui portanto existe

essa esse essa simetria no seguinte sentido e eu volto exatamente ao mesmo patamar aqui e aqui esse lóbulo de fase tem o mesmo formato é desse se eu utilizar um a para cá e o outro a para aqui então é possível aproximar Esse é zero desse Polo por exemplo e esse poderia terminar aqui por exemplo e esse cara aqui poderia ser menor do que o outro mas em princípio trabalharemos com o mesmo a Isso facilita um pouquinho o projeto são restrições que poderiam não ser utilizadas muito bem então estão aqui apresentados os compensadores de avanço

de atraso e esse daqui avanço e atraso nos vídeos futuros veremos o projeto desses compensadores tanto utilizando o lugar das raízes como utilizando o diagrama de B