Distribuições de probabilidades - parte 4

esse bernoulli foi um matemático que desenvolveu esta essas noções de distribuição binomial e ele não fez isso a bem da medicina na verdade ele fez isso para jogar para melhorar a performance nos jogos tá então o governo lhe aplicou esses conceitos que a gente tá falando aqui de nome ao pra melhorar a performance e jogos de azar por sorte nossa que se faz em ciência e desenvolvimento acaba ajudando na área de saúde também né como efeito colateral a produção de conhecimento sempre pode ser aplicado em outra área que não é original isso acontece o tempo

todo para nós na medicina a gente aproveita de todas as áreas do conhecimento para jogar a favor do diagnóstico da terapêutica do tratamento do paciente final né oberli ele estabeleceu que passa a ser válido o processo de nome ao é necessário que os ensaios sejam idênticos ou seja ele pensava na moeda a moeda é um fenômeno jogará moedas saber se vai dar cara ou coroa é um fenômeno binomial cara ou da coroa não vale dizer que ela vai cair em pé porque isso é um acontecimento improvável mesmo que jogue na areia tá certo então é

esse não vale tanto em seu ensaio tem que ser idêntico e tem que ser binomial mesmo só pode dar um ou outro resultado cada ensaio tem somente dois resultados isso aqui tanto que é o sucesso ou falha a idéia de falha não é necessariamente de a ideia negativa acontece que eu tenho que localizar no meu cálculo o fenômeno que me interessa calcular a probabilidade no caso a gente fez parto cesáreo como interesse sucesso seria fazer cesárea falha seria fazer o parto natural evidentemente não é uma falha é técnica nenhuma falha do ponto de vista de

procedimento né indicação de parto natural mas apenas para ele e determinou dessa maneira que quando joga a moeda eu aposto numa delas então se você faz uma aposta de sucesso para você acertar o que você apostou então ele quer calcular a qualidade daquilo que está apostando né então o sucesso eu jogo o valor dp e o valor de que é um - pp para a falha e os ensaios têm que ser independentes essa idéia de independência vai ficar mais clara quando a gente trabalhar no futuro o teorema de vez tá bom então mais independente quer

dizer que quando joga uma moeda na segunda jogada de moeda real aquela que passou não interfere no resultado tá bom então independência dos resultados é bem uma gestante vai ser natural vai ser cesárea vou ver depois vem outra gestante ela não tem nada a ver uma com a outra o fato de ter feito uma cesárea antes não quer dizer que vou fazer um parto normal depois não há dependência os acontecimentos correm em paralelo de forma independente tá lá vamos trazer agora o exemplo para uma situação mais populacional né suponho que eu tenho uma certa doença

aqui vamos e toxoplasmose em que eu sei que a população é foi contaminada 30 teve contágio em 30 por cento das vezes ou seja 30 por cento nos indivíduos da população tiveram foram contaminados com toxoplasmose foi infectados se eu pegar seu sortear aleatoriamente 10 indivíduos qual é a probabilidade estimada de quatro estejam já imunes que já tenha tido essa doença tem um passado pela infecção é importante adquirir uma certa imunidade então a pergunta se entenderam eu tenho uma propriedade de ao sorteará um indivíduo 30% deve ser positivo imune para aquela doença se eu pegar dez

indivíduos quanto eu posso pé e pegar dez indivíduos quatro probabilidade de quatro serem positivos então a idéia aqui é que natureza que filme é esse primeiro qual é a variável a variável é qual tipo atenção falar qual é a variável qualitativa nominal porque é positivo ou negativo imune não imune e tem mais um detalhe é um nominal do tipo só tem dois resultados qual é o tipo binomial só tem dois resultados pela frente portanto é uma variável binomial então já posso usar o que temos são miguel para calcular isso vocês querem fazer na mão pega

10 indivíduos contra aquela árvore com as combinações todas e aí veja quantos quando dá quatro imunes nas suas combinações melhor fazer com a kombi na história não é tão fazer combinatória eu já sei que o pegou a 03 o meu ne10 já tem tudo para calcular o que eu preciso agora pela definição do campeão né usando então a fama geral eu tenho que a probabilidade de quatro indivíduos serem muniz é ele fatorial dessa união x portugal quatro fatores ao 10 menos quatro fatores ao 03 que a unidade ser imune a quarta e 07 que abordar

de ser não imune à sexta fazendo a continha aqui nós temos que 20% de probabilidade de obter quatro indivíduos imunes tá tão fácil deu pra entender bem aqui gente pensa em também é preciso pensar refazer sugiro que você sempre que tem uma um problema dessa natureza refaçam a conta pensem elaborem um pouco e até pergunta e mesmo quando tiver encontro sobre a dúvida está muito bem esta é a curva a distribuição então não há coisa mais vulgar a distribuição da desses dez eventos quando o upgrade interesse e 03 pra qualquer probabilidade de interesse igual a

03 e 10 indivíduos dez eventos eu vou ter essa curva então se jogar no limitado esses dois esses dois parâmetros é igual a 10 e perigosa 03 e obter esta curva aqui como o meu interesse estava em 4 está pintado aqui pra vocês verem que quatro indivíduos e moniz tem 20% de chance de serem obtidos num sorteio aleatório tá o que vocês reparam que aconteceu com a curva com 10 que houve com o formato dessa desse grave fico ele ele ficou mais simétrico né eu aumentei de três para dez e veja o que aconteceu com

o fenômeno há uma certa tendência de centralizar os mais freqüentes os eventos mais freqüentes não estão mais aqui a esquerda assimetricamente com dez indivíduos com dez eventos eu tenho uma tendência de buscar o centro e isso é uma é muito importante porque quanto maior o n mais simétrica vai ficar essa curva a tal ponto que ela se aproxima de uma outra curva notável que nós vamos ver hoje que a curva de gauss tá bom então vejam aqui um exemplo de uma simulação de vários e n eventos diferentes se eu tenho lá os dois eventos já

sabia que ela era bem assimétrica né com majoritária majoritariamente a habilidade de zero que ganhamos as outras se eu vou pra 8 10 eventos e começa a ter uma centralidade se eu vou pra 50 eventos ela fica praticamente simétrica e aqui com 1 350 ora como ela fica dá isso aqui não está ligado os pontos gente olha você que não está ligado mas a marinha é tão fina então e então é tão grande o iene que dá impressão que ela é contínua não dá se eu ficasse aumentar pra mim o seu fomentando indefinidamente isso eu

vou ter uma curva quase contínua eu tenho uma noção tem uma sensação de continuidade e aqui nesse caso eu fica autorizado a emprestar uma outra função que não havia união que a função de ganso mas por aproximação elas não são idênticas mas é muito próximo resultado e gauss é mais fácil trabalhar na prática mas não vejo aqui um pouco isso não fique só com essa noção de que o n importa o ele modifica a maçicamente a o jeito do darfur na vila união quanto maior o ele mais central fica a dispersão dos dados submissão dos

dados caso daqueles que são mais freqüentes tá bom ok vamos passar para a segunda agora uma outra distribuição para probabilidades que há de se cavaleiro aqui o pó som o que acontece quando eu tenho um fenômeno raro um fenômeno binomial raro por exemplo uma distrofia muscular de geração mas é de ordem genética por exemplo se tiveram genética não tenho né então um evento mais raro que acontece por exemplo eu tenho uma manifestação assim em um caso em um milhão a probabilidade de eu achava então caso é um milhão qual é a qual é o complemento

de um milhão é 99,99 999 999 não é então um evento pouco provável quando eu jogo no abdome ao que acontece com ele que dá 0,99 99 99 vezes 0,0001 modifica muito pouco essa multiplicação e quando eu fizer isso com potência vai dando os números assim esquisitos vai perdendo a 0 o evento de interesse entendendo a onde não interesse digamos população percebeu isso para então para eventos raros e propôs o seguinte no caso de eventos raros eventos binomial mais que sejam raros é mais interessante trabalhar a coleção de eventos no tempo então é mais interessante

falar assim olha acontece em três casos por ano de distrofia aqui no hc é um número é raro população de 20 milhões de habitantes de são paulo né ou de 40 milhões do estado de são paulo é errado né três casos por ano mas é significativo é uma doença muito grave mim eu tenho que ter jeito de calcular ele prever certas situações de estimar a probabilidade em eventos raros também e foi isso que o assombrou pra ele a média na verdade é a média histórica de ocorrência daquele evento ela que interessa e não há o

denominador populacional tantos casos em em um milhão não ser tanto não é na por cento mais né o evento raro não é por ser por cento por 100 ele vai ocorrer por milhão por 500 mil então eventos raros são retratados uma maneira diferente e ele adicionou uma nova uma nova um novo elemento que é o número de casos no tempo a média portanto não diz respeito mais há um cálculo daqueles que a gente faz como fez até agora somando e dividido pelo denominador nós somamos os eventos e dizemos eles no tempo então tenho dois casos

por mês 5 casos por ano essa vai ser a nova mesa nova noção de média para o evento aro o tempo então entra como há a noção de denominador né então vem aqui a idéia do pós 1 ele traduz isso aqui a gente usa o lambda lambda aqui eu brinquei que o lambda nada mais é do que um x que teve uma deleção aqui né uma deleção de x mas é uma média também é uma média no tempo o número de casos no tempo e o assunto por construções matemática chegou esta formulação aqui a probabilidade

de um certo número de casos ocorrer é igual à média histórica no tempo daqueles casos então quantos casos por mês quando os casos por ano e levado ao número de casos que me interessa vejo no número joy e que o número de óleo é esse 2,718 são aquelas constantes matemáticas extremamente importante porque elas são boas de curva elas dão curvas maravilhosa nep oilers funciona muito bem para a construção de curvas elas acomodam bem por meio do conselho números racionais elas fazem com que a curva tem uma derivada mas é adequada mais perfeita então tá aqui

ó 2,71 e levado a menos a média histórica - lambda sobre o fatorial do número de casos que me interessa não é difícil não pode ter preconceito vai ser nosso amigo lá é campeão não pode ter preconceito conta contra fórmulas é fez uma cara de meme agora ele acerta não pode não pode acontecer tanto que entendeu né não não fala gabriel fala temos aqui pra isso não é tão não é difícil é são os símbolos são símbolos tá certo então tá lá é uma fórmula simples e não precisa decorar também nada será decorado né sabemos

disso então eu posso me ajuda a trabalhar números de eventos raros transformando a média numa média no tempo e não a média calculada a partir da soma de partes né então é média histórica vão ver um exemplo que depois só que são só as as nossas bases teóricas todo toda toda técnica tem indicações e contraindicações e efeitos colaterais tá certo tudo e na estatística também na matemática também então aqui tem que ter o evento em si independente é eu posso ter teoricamente número infinito de ocorrências acerto eu tenho de deixar livre essa possibilidade é a

ocorrência do evento num dado intervalo é proporcional ao tamanho do intervalo ou seja tudo isso que são co restrições ou indicações ea porção infinitesimal do intervalo para nós não interessa é desprezível a nós interessa realmente trabalhar dentro dos intervalos e não nem infinitesimal no ponto o ponto a gente não tem interesse em servir o interesse no na na faixa de variação diferentemente da binomial comum o dado foi um nome ao adicionar com as ontem a esse tipo de de cálculo de média né o número de eventos vezes a propriedade daquele evento tá onde eu aplico

isso é de maneira por exemplo quer que eu vá parasitas intestinais e tem uma série de aplicações do possam fora dessa estou mostrando que é muito útil em várias técnicas e não só na medicina em várias outras áreas do conhecimento estão com a sua atribuição muito utilizada nós não vamos ouvir falar muito dela do avante na medicina mas ela está por trás de alguns cálculos de gestão gerenciamento então se algum dia no futuro vocês forem pra uma área dessa dessa natureza vão ouvir falar do assunto de novo bom mas é bom saber para calcular eventos

de baixa ocorrência raros aqui o exemplo rápido simples pode aqui se respondeu à questão do próximo ano quem quiser jogar agora tem de ser feito é legal ver a questão já foi atrás e não foi colocada antes da hora fez uma conta não sabendo que o elemento raro de uma forma idade ridiculamente baixo esperem só não estava correta que é só para falar na distribuição e pessoas já não foi procurado pelo zelador foi o google e mídia exterior para cada encontro a distribuição contou após um erro ponto mariana não falou em pontos e sabe que

vocês ganham um ponto sempre fizeram uma tarefa dessa dessa ordem é que resolva o problema sozinho por exemplo certo tá valendo em são paulo nós estamos todos olhando atrás vamos atrás da de vocês fazerem pontos em beleza então a ninguém se vale em nota ok então vamos pegar um exemplo simples aqui o número de suicídios mensais observados numa determinada comunidade é de 2,75 o suicídio por mês de novo caio está lá o e caiu né a média 2,7 de cinco suicídios existe isso não sou eu não é suicídio tá certo não dá pra ficar 34

suicídios não é suicídio então aqui a média resultado que é de uma observação histórica mensal não teve um suicídio no mês 2 no outro quatro no outro e assim vai e faz uma média em 12 meses estabelecem um valor quebrado a média sempre um valor teórico e não tem expressão na realidade certo apenas um valor de referência para dar o ritmo mensal aqui no caso da nossa em dez anos então a observação foi feita essa série histórica e concluiu se que a média de 32,75 é um evento raro é um evento raro vou aplicar o

que então para calcular a probabilidade de ter três suicídios vou usar após um tá certo estão aplicando com ações diretamente aqui a média de 85 e levar a terceira que o número de eventos de interesse número de óleo elevada - lambda que é menos 2 35 sobre três fatores ao seu obtenham 22 por cento de chance de ocorrer um suicídio ou três suicídios naquele mês ou não deterão mês isso então é um filão distributivo se eu tenho 22 por cento de três suicídios tenho de 26 é um outro valor de um suicídio de zero de

quatro eu posso calcular e obter né a curva desta maneira que então essa é atribuição do possam tá bom essa é a cara também deve fazer o militar ambiental a em deste deus um gráfico distribuiu som e escolhe possam e coloca o pagamento dela que a média eo número de eventos que você é é calcular tá certo é que você interessa calcular o a probabilidade muito bem agora vamos falar um pouco daquilo que vai ser mais freqüência nossa vida durante um bom isolante algumas semanas nós vamos trabalhar mais variáveis contínuas agora tá certo vamos parar

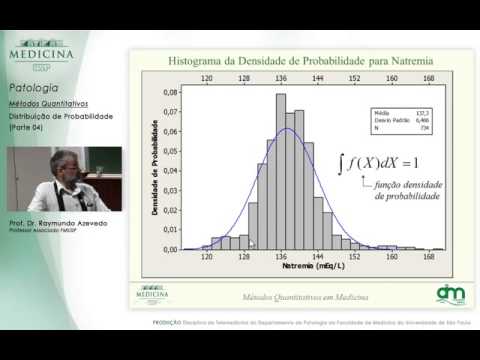
com as outras vão falar mais variáveis quantitativas contínuas porque ela esse destaque nas várias quantas vezes continua até porque ela tem um tratamento estatístico muito característica muito muito útil em várias frentes de de projetos e de produção de conhecimento tá e ela já tem 200 anos de existência de tratamento então é muito ainda ela está em vigor está muito forte ainda como estrutura é de análise estatística então nosso elenco na academia vamos retomá los já é bem conhecido de todos têm aqui a distribuição dos dados à disposição bruto dos dados sem nenhuma análise por trás

apenas a contagem de cada de quantos indivíduos estão em cada um dos valores aqui tributos portanto os 734 devidos nos vários valores na temia tá muito bem se eu fizer um estou grama desta desses dados já modifiquei a criar um gráfico de barras eu faço o histograma desses dados e obtiveram a média do padrão com esses dois parâmetros médio padrão eu consigo ter é passar a curva de gauss aqui porque os padrões da curva de gauss são apenas a média do padrão então você tem um conjunto de dados contínuos variáveis contínuas eu posso calcular médio

padrão eu consiga obter uma curva que representa daqui pra frente aqueles dados nesse caso aquilo que vocês percebem esta curva evidentemente esse programa não é perfeitamente simétricos porque ele é fruto de uma de uma obtenção de uma mostra nenhuma amostra perfeita nós tentamos reduzir sempre os erros amostrais mas sempre temos que ter em consideração que nenhuma amostra vai ser perfeita ela nunca vai ser replay na mente representativo é por isso que nós tentamos a partir da amostra constituir uma curva que represente a população então o pulo do gato aqui é sair dos dados brutos para

os dados que seriam assim os dados representativos da população eu posso fazer isso usando uma curva a curva de gauss existem técnicas aqui pra gente verificar se esta curva realmente representa esse conjunto tá então você está olhando aqui pra mim falar assim mas a coisa não está muito bonita não se eu pudesse puxar ela pra cá um pouquinho né é tentar essa esse top dela que o ponto alto dela está um pouco abaixo daquilo que seria esperado nos dados brutos né mas o problema é que eu tenho valores aqui extremos dos dois lados que estão

perturbando a média a média está não está perfeitamente estimado porque tenho valores aqui estão muito extrapolado us 1.170 de sódio 116 de sódio muito muito muito forte na curva talvez não esteja correta esse valor mas foi o dado que eu peguei o dado bruto eu posso criticar meu dado e refazer e eventualmente mas nesse caso aqui é fazê lo significa refazer o exame laboratorial né está novamente esse novo uma diluição daqui é o colírio eu colhi o azar de sódio com soro glicosado para na veia do soro glicosado vou lá e tiro uma amostra de

sangue bem diluído de lei com soro glicosado tá errado o procedimento então e 116 não parece fruto de e como no pronto-socorro alguém foi lá achou que mais sofre cada vez que já estava canale da sta é lá disponível não é e acaba fazendo um erro técnico de coleta muito bem por que então o que a gente faz essa curva porque o dado bruto o dado àqueles pacientes não é o da população verdadeira também ele está arrebentando representar então prefiro trabalhar com a média do sul porque no final das contas o que me interessa é

conhecer a variação o que importa não é o valor tão perfeitamente em cima dos pontos amostrados daqueles pacientes específicos o que importa é que a média e desvio padrão compõem uma noção de variação do fenômeno né então tá aqui agora eu posso trabalhar com a integral em baixo da curva se eu quiser saber uma certa faixa de interesse com a probabilidade de ocorrência o cálculo da curva e não mais nos pontos da dos pacientes mesmo isso é muito importante porque agora eu faço a inferir para a população a minha ideia nunca trabalhar aqueles pacientes aqueles

pacientes servirão para que eu tivesse uma estimativa de média desvio padrão para aplicar a curva de gauss e aí tem na curva de gauss eu posso finalmente fazer as contas em baixo da curva eu tenho uma área que eu posso calcular o valor de probabilidade embaixo da área tá certo essa área mas pintadinha de vermelho que a minha região de interesse por algum motivo agora específico eu posso saber qual é a probabilidade de ocorrer naquele intervalo então esse é o pulo gente porque eu faço todo esse esforço eu vou a campo coleta o sangue idosos

planilha analisa o histograma cálculo médio padrão e assalto fora porque quem sobrou médio padrão a minha mão é suficiente porque eu tenho uma curva que eu consigo trabalhar tudo que eu quiser em termos de probabilidade você vai fazer só me somas dos intervalos de cada valor unitário eu acabou isso aí é estória eu só usei aquilo para obter a média do padrão e por tabela a curva de gauss tá bom então esse é o ponto nós queremos representar a população tá aí pra vocês não dizerem que nunca viram a fórmula da curva de gauss esta

é a famosa função calce ana ela envolve o valor pi como eu falei o pior é o e são ótimos eles entre muitas curvas notáveis tá então são dois números essenciais apesar de racionais eles sempre trabalham a favor de curvas batom bem bem comportados e bonito né tá aí um sobe 2 p a escola do isp vezes o desvio padrão agora que é interessante para nós há desvio padrão vezes o elevado a menos x - média então os pais são média e desvio padrão ao quadrado sobre duas vezes a variância então com desvio padrão e

com a média eu modifiquei as características de qualquer curva normal então o normal a ficar mais alta ou mais larga dependendo de se o padrão vai se deslocar para a direita ou à esquerda pela média então eu só preciso desses dois parâmetros o resto é constante aí né o pio e são números constantes o número 1 também evidentemente ataque só preciso de médio padrão isso é muito muito favorável é o sonho de qualquer pesquisador é poder reduzir seus dados a um valor médio ea e conhecer a variação em torno da média conhecer o padrão nós

se nós pudéssemos nós trabalharemos sempre com variáveis quantitativas contínuas porque queria tudo muito mais simples e de tratar estatisticamente isso não será sempre assim vocês vão ver daqui umas semanas que não tem que lançar mão de outras técnicas porque as variáveis nominais por exemplo não permitem esse tratamento eu só posso usar a média do padrão para variáveis quantitativas as contínuas certamente as discretas depende então eu vou ter restrições tudo que não for variável quantitativa contínua vai me impor algumas algumas restrições vão ter que fazer perguntas adicionais para poder usar esta ou aquela técnica estatística mas

no nosso caso aqui hoje variável contínua curva de gauss médio padrão é o que nos importa nesse momento ea é quem que se pudesse usar sempre contínuo as variáveis contínuas seria maravilhoso que há até quem são as mais simples mas mais poderosas são as as que têm acordo legal se como base está bom muito bem vamos ver um pouquinho da anatomia da curva normal já perceberam que a krona mais simétrica né ela vai de menos infinito a mais infinito ea média dividir a curva área da curva em baixo da curva e perfeitamente em duas metades

iguais então é uma curva perfeita ser perfeitamente simétricas ela nunca encosta no plano no eixo x a curva normal nunca em costa não é justiça tá ela é assintomática ela decaia sintomaticamente até o infinito e até mesmo os infinitos mas qualquer forma está aqui a média divide em duas metades idênticas ela tem uma outra característica importante que são essas regiões delimitadas pelo desvio padrão com um desvio padrão a esquerda ea direita nós temos que a área azul escuro aqui demonstrada abrange 68% da propriedade acontecerá naquela naquele intervalo então isso é muito cara qualquer curva normal

qualquer curva normal tem uma área de 68 por cento aproximadamente quando nós consideramos o primeiro desvio padrão em torno da média a esquerda ea direita tá então isso aqui é pra qualquer curva normal e aí que entra a graça de trabalhar com o valor normal esta propriedade a propriedade estável se eu tenho médio padrão eu sei essas regiões aqui delimitadas por desvios padrão são muito muito bem conhecidas então o cálculo com facilidade a habilidade em baixo do que o normal tá bom então fica bastante simples aqui com dois desvios padrão a esquerda ea direita nós

temos 95% de cobertura que nos dá então a nós sabemos que 95% da de probabilidade de ocorrer naquele intervalo entre -2 o padrão em torno da média tá tudo isso é importante importante começar a gravar esses números característicos né porque você raciocina rapidamente olhando para o normal e com três desvios padrão nós chegamos no limite quase dos 100% 99,7 por cento por isso que com três desvios padrão para a direita e esquerda eu tô com quase totalidade adianta apresentar um quadro de padrão vai se somar o que vai ser amanhã 03 que não encosta né

então daí pra frente o 5º c o padrão se esse padrão já não adiciona mais nenhum significado porque são os valores muito extremos né o que me interessa conhecer são os valores comportados em torno da média área fisiológica neve ou seja a região fisiológica de comportamento de um eletrólito de uma proteína de uma áudio de um de um carboidrato como a como a glicose não me interessa muito saber valores e os valores extremos são os patológicos na cidade eles podem até pertencer à distribuição eventualmente mas a nós na medicina a partir do terceiro dia o

padrão geralmente significar a alteração patológica ou seja a pessoa está doente uma vez e meia de 200 vai estar lá na no 10º dia o padrão da curva de glicemia distribuição de glicemia nos humanos eu sei que esse indivíduo já está com um evento com diabetes mesmo eu tenho uma definição clara e é assim que nós estabelecemos valores muitas vezes de referência no laboratório a partir da distribuição montada com a krona mal inclusive a vir à casa em que eu tenho que usar outras curvas mas o normal responde por boa parte do valor de referência

em laboratório para variáveis quantitativas contínuas tá bom então essa é a anatomia básica aqui do nosso curso se eu pegar com agora de novo exemplo de natanya nós sabemos que a faixa de variação na academia não pode ser 170 116 né mano a pessoa não sobrevive com valores extremos assim de sódio série então nós já delimitamos aqui pra exemplificar as três regiões a região fisiológica a região hiper na técnica ea região hiponatremia as coisas não estão muito bonitas aqui porque porque o n por exemplo de ipê na tv é pequeno tem tem 41 indivíduos apenas

com o sódio aumentado então ficou uma coisa feia né quarenta e um indivíduo não faz uma curva simétrica adequada mas se eu pegar a média do padrão de cada uma dessas regiões e fizer as coisas normais sozinhas agora sem os dados eu tenho isso aqui reparem que com a média do padrão possui três curvas normais as três são gauci anos mas ela tem um jeito diferente porque uma é mais baixo e mais larga que essa do ipê na tribo que tem só 41 indivíduos que de onde saiu o cálculo né a hiponatremia que é um

tipo mais alta e mais estreita com o seu padrão menor largo quer dizer se o padrão maior estreito do padrão menor e finalmente a faixa fisiológica que contempla um maior número de pacientes 408 pacientes ea onde o padrão pequeno e uma um comportamento bem mais regular bem mais é previsível né então se nós pegamos aqui que o que se observa nessa neste gráfico as três curvas se interpenetram e essa interpretação é o nosso problema uma pessoa que tem hiper na temia uma alteração patológica que faz e pela família na verdade o grupo muitas vezes pode

ser mostrado e cair numa faixa norma na tréplica fisiológica osipova tempos também podem chegar até alguns a fazer o ipo não treme eventualmente porque porque se eu fizer a medida de vocês aqui eu pego uma é um de vocês aqui sento aqui foi um eletrodo de sódio em cateter é com eletrodo de sódio na circulação venosa central e fico registando sódio você acha que essa é uma linha reta não vai ser uma linha que flutua ela tem uma o sol vai ficar avaliando que a consumo a ingestão a meta a inscrição do sódio então vai

ficar uma linha ou ciranda em uma faixa bem definida algumas pessoas vão fazer uma faixa um pouco mais ampla de variação do sódio quando eu vou lá e colho o sangue eu posso pegar num momento que ele está numa faixa mais alta e aí eu perco diagnóstico né ele é igual a 3 mas ele acabei dando normal para ele naquele momento mas ele contém um sintoma então o acordo de novo às vezes até de uma hora que a gente surpreende o fenômeno não é esse é um complicador da nossa profissão os exames laboratoriais também variam

de acordo com alguns algumas características fisiológicas né ninguém tem glicemia é preso ela tá comendo um sanduíche na li sétima que chama aberta e ela está comendo sanduíches tinha certo e aí agora ela o pão amilase já vai pegar e vai produzir glicose na própria boca e vai absorver glicose a minha senha dela já não está mais 80 deve chegar agora a uns 90 e pouco né então vamos supor que se eu fizesse um eletrodo naná beatriz agora de glicemia ficar monitorando ela chegou aqui a aula foi gasta energia a ela como seu leitinho aumenta

de corda e baixo tá a a uma variação essa coisa não está mostrando avaliação do indivíduo mas a variação de surpreender um conjunto de indivíduos então preciso ter em mente que a faixa fisiológica às vezes atravessa eu vou lá e como uma boa espumado e como churrascos salgados certo ingerir sal muito sal eu vou de repente tem uma variação para cima do meu saudável só dê certo absorvendo né essa essa vai ser corrigido vai ser cantado pela pelo rim o excesso mas enquanto isso se fizer um exame ali nas imediações da do churrasco pode ser

que eu mostro meu meu só de um pouquinho ele por isso que a gente tem coletar exames com uma certa padronização o jejum por exemplo de oito horas hoje 6 horas dependendo hálito é fundamental para padronizar porque eu sei que vou pegar o indivíduo num certo num certo momento de metabolismo como uma feijoada e vou fazer eles e mia não está certo vai dar uma alteração brutal mas não passou e diagnóstico com isso tem que fazer uma coleta de padrão ou seja com certas características bem de conhecidas então a interpenetração é nosso problema na estatística

porque se eu quiser saber se esse grupo é diferente de si e esse grupo é diferente de si eu tenho que ter noção de que a variação implica em que os valores podem se interpretar em algum ponto mas com baixa probabilidade a probabilidade mais alta está fora da curva a mais ao está fora desta curva mas isso é uma zona cinza aqui de entremeio né de de de interpretação das curvas que é que eu vou ter que aprender a trabalhar daqui pra frente então as próximas aulas nós vamos começar a mexer com esse das curvas

normais com as curvas de gauss e vamos aprender a lidar com esta como é que o desembaraço das curvas enquanto que é significativo o afastamento das médias então será que a média do grupo fisiológico está longe o bastante da do ipê na treme pra que eu diga que elas são diferentes e esta é a pergunta por trás de todo o curso quando comparo grupos quando comparo populações eu quero saber se elas são diferentes eu tenho que levar em consideração a distribuição por trás como o que está regendo a atribuição daquele daquela variável e aí sim

eu vou determinar como a certo grau de erro se elas são iguais ou são diferentes então comparações é que está no nosso cardápio nas próximas aulas está essa dizer que a curva normal pra ser útil ela é não posso fazer uma curva para o colesterol é uma coisa glicemia uma curva pra sódio para votar sete para cada variável contínua é melhor ou padronizar eu tenho uma curva padrão e como é que eu faço a padronização da curva é o que me interessa é o a curva e as suas propriedades características de propriedade não é então

montar para cada analista uma curva do t 2000 curvas não é bom trabalhar com os micros seu lançar mão da padronização eu vou ter uma tabela que me dá todas as probabilidades de baixo da curva de gauss que a tabela z e como é que a gente padroniza isso basta que eu pra calcular um z padrão que é o número de desvios padrão ser nada mais é do que o número de desvios padrão padronizado basta que eu pegue o valor que me interessa a minha variável de colesterol por exemplo - a média do colesterol sobre

o padrão do colesterol é bom ter um valor dizer que me mostra quanto se afasta da média aquele valor de interesse vamos tratar isso aqui é a distância da média e aqui a métrica da distância de avaliação de novo lá caiu em média uma prestação mas é importante como referência para que eu jogue os desvios padrão e veja quanto crises enquanto que varia em termos de desvio padrão da média tá bom muito bem se você for mal que fizeram quer dizer que a o meu valor a variável que interessa aqui no caso o valor da

minha variável é maior que a média se usei melhor que zero menor é o x é menor que a média no caso de uma tabela z a média é tida como zero na curva de gauss roda uma curva de gauss comédia 0 e deu padrão igual a um porque tudo foi organizado para esta para esses dois parâmetros 10 e 11 tá ok aí eu posso participar após fazer os cálculos a partir das outras regiões notáveis que agora virou zero como centro e um desvio-padrão 23 não tá parecendo um valor mais da minha variável eu sumir

com a unidade própria da variados como colesterol glicemia e coloquei agora tudo o número puro então a curva padrão é uma curva gerada com números puros 100 unidades sem ele não contempla qualquer unidade está certo o que é interessante é que a gente faça cálculos mais facilmente aqui temos o exemplo do colesterol nós fizemos aquela se vocês se lembram nós fizemos uma amostra entre estudantes de medicina numa classe e patologia clínica e foram somaram 53 voluntários obter uma média de 137,9 miligramas por decilitro eo padrão de 32,3 miligramas por decilitro muito bem se eu quiser

agora veja que agora o importante para nós é que os dados brutos que estão aqui em cinza perdem a função saem de cena sobra a curva normal mas imaginem vocês fazer cálculo integral agora para calcular a probabilidade e baixo da curva seria bom seria interessante usar cálculo integral aqui é possível mas é muito trabalho é melhor padronizar sair desta curva do colesterol para uma curva padrão uma curva z e colegas vão fazer isso vamos lá suponho que eu queira determinar a probabilidade de sortear qualquer um de vocês aqui pra cair entre 90 ea média sim

67,9 qual a probabilidade de que o sorteio onde vocês mestre colesterol e caia nessa faixa entre 95 67 eu posso calcular sua mão com o cálculo integral né não é uma boa ideia vamos fazer isso da maneira padronizada basta que eu tire 90 de 167 ou contrário 90 - 167,9 sobre o desvio padrão eu vou obter o número de desvios padrão que 90 se afasta de 167 como é que fica essa conta o z que é o número de desvios padrão longe da média é igual a 90 - 117,9 sobre 32,3 o meu z portanto

é igual a menos 2,41 de desvios padrão não é mais miligramas por decilitro agora porque o padrão disney eu corto cortei em cima que era miligramas em cima aqui embaixo também miligramas cortou ficou número puro então ficou apenas no número de desvios padrão que 90 se afasta da média então eu tenho esse intervalo - 2,41 agora vou tabela z a tabela z nós não vamos usar na prática nós vamos usar o militar que calcula pra mim usei calcula a probabilidade de que interessa naquela área mas só para vocês saberem que isso existiu e até a

turma do da dani 97 até todo o dano por exemplo 97 a gente fazer isso num acerto e daí a razão de uma certa as críticas aparecerem é historicamente por que fazer na mão está é mais complicado não complicado mas é trabalhoso né e aí nós somos mais práticos pragmático e menos ao computador então 12 e 41 lembra o valor 2,41 desvios padrão como funciona essa tabela tabela funciona assim ó os dois primeiros números o inteiro e o primeiro desse mal vem nesta coluna e o segundo desse mal centesimal na verdade vem aqui então do

cruzamento desses dois eu tenho a área ea área no caso 0,49 2012 ou seja a probabilidade de cair um índio sortear o indivíduo desta sala agora ele está entre 90 e 167 é de 49% então eu consigo fazer cálculos de probabilidade a partir desse tipo de raciocínio faz seu favor bianca para poder usar essa tabela é na verdade o que me interessa não é mais o 9167 mas é quanto um se afasta do outro desvio padrão então estou eu padronizem na verdade é esse intervalo tem 2,41 desvio-padrão o valor de r 60 e de 77

a distância de 95 67 77 miligramas certo ele não tem significado para mim ele diretamente eu não consigo entender o que eu estou dizendo aqui 90 está a 2,41 desvios padrão do da média então ele está bem longe entendeu a idéia se eu falar você 90 está no valor 90 miligramas por decilitro está a 77 miligramas por decilitro da média isso não está traduzido em termos de distribuição eu preciso padronizar em desvios padrão e é preciso trazer tudo para uma conta que me dá à distância da média a distância padronizada entendeu a idéia agora então

transformei o valor 77 em 2004 31 dos fios é essa quem é o nosso interesse é usar sempre um recurso que me facility compreender a exibição do fenômeno isso vai ser muito importante porque eu vou ter q comparar com outra curva no futuro na prática o que eu vou fazer é uma média distância da outra média será que elas estão afastadas o suficiente para que eu digo que são diferentes enquanto se o padrão tem de se definir para dizer que elas são diferentes então toda esta nós estamos chegando aqui numa certa conclusão agora é importante

porque tudo que eu fiz até agora foi para chegar nesta simplificação então transformamos os nossos dados brutos numa curva contínua e esta continua e fornece a distribuição padronizada em desvio padrão quando o avante nós vamos trabalhar com estas ferramentas com esses poetas é é esta abordagem para poder comparar coisas com para grupos comparar populações combinado muito bem então encerra por aqui a aula teórica