TUDO de Matemática do Ensino FUNDAMENTAL pro ENEM 2025 (pra quem tem MUITA DIFICULDADE)
199.11k views147756 WordsCopy TextShare

Pedro Assaad | ENEM 2025
🔥 Inscrições abertas para Plataforma Assaad com todos os bônus inclusos!!! VAI ACABAR A QUALQUER MO...
Video Transcript:
Opa, fala galera, professor Pedro Assad na área. Nesse vídeo aqui eu vou te ensinar toda a matemática do ensino fundamental, aquela bem basicona que você deveria saber, tá bom? Pro Enem, que se você não sabe ela, você com certeza tá com muita dificuldade de evoluir em matemática. Então, é um vídeo que, sinceramente, ninguém faz, né? Porque é matemática muito básica mesmo. Então, assim, eu tinha falado que eu ia fazer um vídeo com tudo de matemática básica pro Enem 12 horas. Só que, galera, ã, primeiro eu precisei fazer um vídeo de toda a matemática básica do
fundamental em 12 horas, que é esse vídeo aqui que tá na sua mão agora, tá bom? Então, esse vídeo aqui ele não é para cobrir toda a matemática básica do Enem, porque ele não vai cobrir, por exemplo, razão, proporção, a gente não vai pegar aqui escalas. Esse vídeo aqui é só a matemática fundamental mesmo, é a matemática que ela é a básica básica que ninguém ensina. Então, por exemplo, esse vídeo aqui é o quê? soma, subtração, é multiplicação, divisão. Esse vídeo aqui você vai ter muita potenciação e radiciação. Muita. Então, potenciação e radiciação, tá? Tá,
tá, tá, tá, tá, tá, tá, tá. Muita potenciação e radiciação nesse vídeo aqui, mmc, mdc, basicamente isso. Então, tem muito mais coisa, né? Eu mostro muitas técnicas, eu mostro muita podivisão de e e frações, tudo sobre frações. Soma de fração, eh, multiplicação de fração, divisão de fração, subtração de fração e exercícios resolvidos. Aqui nesse vídeo aqui a gente vai ter mais de 150 exercícios resolvidos, tá? E é isso, bizarro, tá? Depois eu vou pegar a lista de exercícios toda dele, vou separar e vou deixar aqui para você pegar no link da descrição, mas agora no
momento que o vídeo tá sendo postado, se você tá vendo já agora, ainda não vai ter. Então estamos conversados. Você entendeu o que que vai ter nesse vídeo aqui. Esse vídeo aqui são 12 horas de toda a matemática básica, básica, básica, né? matemática do ensino fundamental mesmo, fração, fração, potenciação, radiciação, coisa que você não sabe. E aí, por saber, você tá com muita deficiência, com certeza, tá? Durante o vídeo, eu vou resolver, sei lá, 150, 200 exercícios contigo, muito exercício mesmo, é uma tonelada de exercício que tem nesse vídeo e eu vou ficar vindo aqui
toda hora no vídeo te lembrar. Então, toda hora eu vou aparecer aqui no vídeo. Opa, muito bem, você tá concluindo, né, para você ter uma noção do teu progresso. É claro, se você tá assistindo aí durante o evento Operação Medicina, vai ter aula ao vivo hoje, né, para quem tá assistindo às 77 da noite tem aula lá. Eh, outros avisos, né, aqui no YouTube eu vou postar mais aulas ainda, né, com tudo de matemática básica. Então, a próxima que eu vou postar realmente vai ser tudo de matemática básica, é completa, né? Já já pegando razão,
proporção, regra de três simples e composta, escalas, conversão de tempo, de unidades, mas essa aqui agora ela é muito focada em quem tem muita dificuldade. Essa aula aqui agora é para quem tem muita dificuldade, mas mesmo que você não tenha muita dificuldade, você vai aproveitar se você assistir, tá bom? Então ela vai começar e ela vai ficando cada vez mais rápida, vai pegando cada vez mais tração. Mas, ó, critério de divisibilidade, múltiplo, divisores, frações, tudo você vai ter aqui. Outra coisa, caso quando você tiver assistindo a plataforma SAD já esteja disponível pra compra, no momento
não tá, vai ter um link aqui embaixo. Então, não deixa de considerar a possibilidade de assinar a plataforma SAD e ter muito mais conteúdo do que isso aqui, só que sempre de modo muito organizado, de modo muito perfeito para você ter todas as aulas de todos os assuntos comigo, tá bom? Porque eu me considero mesmo o professor que tem a melhor didática, a melhor sensibilidade para ensinar do Brasil inteiro. Meus alunos também consideram isso. E você vai gostar bastante se você assinar a plataforma S. Então, o preço normal é 3.000, mas deve ter alguma promoção
rolando. Vai tá no link aqui de baixo. Se tiver, se não tiver, aguarda que daqui a pouco vai ter, tá bom? Então é isso, cai dentro da aula que isso aqui vai fazer uma diferença absurda na sua vida, pode ter certeza. Nenhum tempo aqui vai ser perdido, vai valer mais do que você acompanhar o cronograma do teu cursinho, provavelmente, porque isso aqui vai desbloquear tua inteligência matemática. Então, ó, vamos nessa. Tô contigo sempre, hein? Não deixa de curtir o vídeo, comentar, porque eu eu dependo do engajamento de vocês para fazer isso. Se eu postasse isso
aqui e não desse visualização, o engajamento eu não postaria, tá bom? Então, depende de você curtir a live, comentar, vai dizendo onde que você tá nela e vamos para cima. Vamos lá. Por que que eu tô dizendo que o nosso sistema de numeração é decimal? Porque tudo que a gente tem, todos os números que a gente tem, eles são construídos com base em 10 coisas. E essas 10 coisas são os algarismos. Então, o que são os algarismos? Os algarismos são justamente as peças que constrem qualquer número, tá? Qualquer número são, como eu tava dizendo, os
algarismos são as peças que constróem absolutamente qualquer número. Quais são os algarismos? Isso é uma coisa simples e é óbvio que você tem que saber imediatamente. Então, 1 2 3 4 5 6 7 8 9 0. OK? Esses são os 10 algarismos. Você pode contar e você vai ver 1 2 3 4 5 6 7 8 9 10. São 10 algarismos. E esses 10 aqui e a gente só precisa deles para construir absolutamente qualquer número. Mas talvez você diga: "Mas como que é possível que só com essas peças aqui e só essas eu não tenho
mais nenhuma peça para usar, eu consiga construir qualquer número? É justamente por conta do segundo tópico. Então só queria dizer que o primeiro tópico tu já pegou, beleza? Algarismos. É isso aqui. A gente acabou de de já encerrar o primeiro tópico. E quando você combina algarismos, você tem um número. Então, por exemplo, se eu pegar aqui, ó, 13, isso é um número. Se eu pegar aqui, ó, 34, isso é um número. Se eu pegar aqui, ó, 456, então 456. Isso é um número. Se eu pegar aqui, ó, 8 74 3, 8 74 3, 8743. Isso
é um número, tá? Só que você vai perceber que, ué, mas como que a gente forma todos os números infinitos, números que não acabam mais? Usando isso aqui, é porque além de usarmos os algarismos, a gente usa um sistema de posição. Dependendo de onde eles estejam, eles podem valer mais, valer menos, eles podem mudar o seu valor. Isso é o que a gente chama de valor absoluto e valor relativo. Então, a primeira coisa é você dominar o valor absoluto, tá? O que é o valor absoluto? O valor absoluto é o valor do número mesmo, é
o valor do algarismo mesmo. Por exemplo, vamos lá. 135, qual é o valor absoluto do 1? Um. Cada algarismo tem um valor absoluto e um valor relativo. Qual é o valor absoluto do um? 1. Qual é o valor absoluto do três? 3. Qual é o valor absoluto do 5? Vai respondendo junto comigo. 5. Tá? Pega aqui, ó. E 4598. Qual é o valor absoluto do 4? Quatro. Qual o valor absoluto do 5? 5. Qual é o valor absoluto do 9? Nove. Qual é o valor absoluto do oito? oito. O valor absoluto de um algarismo é
o próprio algarismo. Só que eu agora pensa aqui comigo, mais um exemplo, mais um exemplo ainda antes da gente partir pro pro abraço do conteúdo de fato, pensa aqui no 7 7. Qual é o valor absoluto do sete? Sete. Qual é o valor absoluto do sete? Sete. Qual é o valor absoluto do sete? Sete. Só que tem uma coisa aqui. O nome do valor absoluto, o que que significa uma coisa absoluta? é uma coisa que não depende de nada, é uma coisa que ela é ela mesma e ponto, não depende de nada. O algarismo 7
sempre tem valor absoluto sete, porém existe uma coisa chamada valor relativo. E o que que é uma coisa relativa? É uma coisa que depende de alguma outra coisa. Então, se eu falar para você assim, ó, você gosta de comida? Se eu falar assim, ó, comida, que que é melhor? Comida japonesa ou churrasco? Aí você fala assim, ó: "Iso é uma coisa relativa." O que quer dizer uma coisa relativa? Você tá querendo dizer o que? Ó, depende de quem? Eu vou te perguntar assim, ó, relativo a quê? Aí tu fala assim, cara, relativo ao gosto pessoal
de cada um. Então, para mim, por exemplo, em relação a mim, em relação, ou seja, relativo a mim, comida japonesa, mas relativo a ele, em relação a ele, é churrasco. O que que é o valor relativo de um número? É justamente o valor que é o valor meio que quase que o valor mais importante dele. Porque esse valor relativo, ele é relativo à posição do número. Por exemplo, dá uma olhada aqui no 135. Qual é o valor absoluto do número 5? cinco. Mas qual é o valor relativo do número cinco? O valor relativo do número
cinco também é cinco. Eu tenho quantas coisas aqui? Eu tenho 135. Tu vai falar: "Porra, Pedro, então o valor absoluto e o valor relativo são a mesma coisa?" Não, tu vai perceber agora a diferença, tá? Olha pro três. Qual é o valor absoluto do trê? Três. Valor absoluto do trê é 3. Mas qual é o valor relativo do três? 30. O 3, na verdade vale 30. Tu tá olhando aqui o 135 e aqui tu só vê um algarismo 3, mas na verdade o valor relativo desse cara aqui é 30, não é 3. O relativo é
30. E qual é o valor relativo desse número um? O absoluto é um. Mas e o relativo? Ele é um 100. Esse número aqui, ó, como é que você sabe que ele é um 100? Olha o que você tá falando. 135. Ou seja, o fato desse um estar aqui faz com que ele valia 100. Ou seja, esse um aqui, na verdade, é isso aqui, ó, 100. Ou seja, você já viu que esse um se combinou com o número zero duas vezes aqui e ele é o 100. Então, vamos ver o que que tá dentro desse
número aqui, desse 1 35. O que que tá dentro dele? Tem ali um 100 que tá oculto aqui, né? Então a gente tem um um que tem um valor relativo de 100. Aí tem aqui um 3 que tem um valor relativo de 30 e tem aqui um 5 que tem um valor relativo de cinco. Ou seja, o valor do cinco, o valor relativo do cinco é o próprio valor absoluto dele, tá? E que que eu tenho aqui? Quando eu tenho 100 + 30 + 5, eu tenho qu, ó, leia. 130 é 5. Isso pode, primeiro
que isso aqui já cai no Enem, isso aqui já é uma coisa que te ajuda a acertar questões, mas isso aqui, acima de tudo, te ajuda a fazer operações matemáticas, tá? Às vezes, é por isso que você não consegue fazer operação matemática mentalmente, porque quando você pensa assim, ó, vou fazer aqui, ó, 2 x 135 de cabeça, o mecanismo normal é você fazer o quê? 2 x 100 200 2 x 30 260 e 2 x 5 10 270. Algumas pessoas não conseguem fazer isso e é porque na verdade elas não têm a sensibilidade de fazer.
Ó, você viu como é que eu fiz? Eu decompus o número, fiz duas vezes 135. Aí sem olhar para isso aqui, eu consigo saber de cabeça que é o quê? Primeiro eu faço 2 x 100 porque tem aqui um 100 escondido. Eu já vejo um número abrindo. Tem um 100 ali. 2 x 100. 2 x 30 não, 35. 30 que dá o quê? 60. Então, 260 e duas vezes o 5 que é 10, fecha o quê? 270. Tá? Então isso aqui é só um exemplo de como que você conhecer essa essa essa noção. Não é
conhecer, não é apenas conhecer. Essa noção, ela tem que tá enfiada dentro do seu cérebro, tá? Ela tem que tá eh grudada na sua mente. Beleza? Isso aqui é realmente fundamentos da matemática, tá? E você vai ver como que rapidamente isso aqui cresce. Parece agora no início, ah, Pedro, isso aí é uma coisa simples. Até é uma coisa simples que ninguém para para explicar hoje em dia nos cursinhos, tá? Então, é por isso que eu te garanto que o método aqui vai funcionar. Olha pro número qu e 4598. Vamos lá. O valor absoluto de todo
mundo, a gente sabe o valor absoluto do 4 é 4, do 5 é 5, do 9 é 9 e do 8 é 8. Beleza? Até aí não tem novidade. Agora vamos lá. Qual é o valor relativo do número quatro? Qual é o valor relativo do número quatro? Ele pode parecer um quatro inocente, mas na verdade ele é o número 4.000. Tanto que se você falar isso aqui, tu vai ter que dizer o qu, ó, 4598. Então o 4 é o 4.000. O 5 na verdade ele é um 500 oculto aqui, tá? O 9 na verdade
ele é um 90. E o oito é apenas o próprio oito mesmo. O valor relativo dele é o mesmo que o valor absoluto nesse caso. Beleza? 4598. Olha que incrível, né? Agora olha aqui. É o mesmo número. É 77 7. Qual é o valor relativo desse primeiro set? É 700. Qual é o valor relativo do segundo set? é 70. Qual é o valor relativo do terceiro set? Ele coincide com o valor absoluto. É o próprio set. 777. Você talvez você nunca tenha percebido isso na sua vida, que na verdade você fala os números justamente assim,
você fala os números dizendo o valor relativo de cada termo dele, né? 777. Agora, se eu perguntar para você assim, ó, quanto que é? Eu sei, ó, não tem problema se você não souber fazer agora. você tá na primeira aula da plataforma SAD, não tem problema se você não fizer o que eu vou te falar agora, se você não souber, tá bom? Mas eu só quero abrir tua mente para isso. Vamos supor que eu te pergunte assim, ó. Quanto é de cabeça 3 x 77? Tá. Quanto é 3 x 77? O raciocínio deveria ser o
quê? Ó, 3 x 700, que dá 2100. 3 x 70 que dá 210. Então 2100 + 210, já tenho 2310. E 3 x 7= 21. Então 2331. 2331. Isso você só consegue quando você tem na sua mente essa habilidade de rapidamente separar, de rapidamente decompor os números, tá bom? E aí, só para deixar muito claro para você, que eu acho sempre importante que eu diga isso nas aulas, tá bom? Isso aqui realmente cai no Enem. Tem muita gente que pensa assim: "Não, isso aí, isso cai no Enem para isso tá presente em várias matérias". Mas
no o Enem sempre tem uma ou duas questões que é só isso aqui, ó. Leia esse número. Ele bota um número grande e fala assim: "Leia esse número. Que número é esse? Quantas vírgulas tem nesse número? Quantas casas tem nesse número? A galera consegue errar e quem erra na h da prova é uma completa tragédia pro tri, tá bom? Então, mais uma vez a gente fechou aqui mais um tópico que é o tópico do valor absoluto contra o valor relativo. Vamos agora dar uma olhada só num número maior pra gente fixar isso, tá bom? Então,
vou colocar aqui um número grandão e a gente pode fixar isso agora, tá? Então, vamos lá. Se eu colocar aqui, por exemplo, o número, sei lá, vou escrever aqui aleatoriamente, né? Vou escrever qual que é o número aqui, ó. Pronto. Então, coloquei aqui, ó, ã, 1.77.594. Vamos lá. Vamos colocar o valor relativo de cada um, porque o absoluto a gente sabe que é o próprio algarismo, né? Então, o absoluto do 7 é o 7, do 6 é o seis, tanto faz. Agora vamos colocar aqui embaixo os valores relativos. Então, qual é o valor relativo desse
um aqui? Ele parece um inocente, é só um número um. Na verdade, o valor relativo dele é 1 milhão. Para você saber o valor relativo, tu pega o número, tu vê quantas coisas tem depois dele e tu completa tudo aqui com zero, tá bom? Então você vai ter uma noção, tá bom? Na verdade, para ele estar aqui, tivemos já que recuar 1 2 3 4 5 seis casas e depois vem ele. Então essas seis casas, na verdade, são zero. Então aqui, ó, ele é 1 milhão, tá bom? Então só aqui eu tenho 1 milhão. Qual
é o valor relativo desse sete aqui? Deixa eu ir colocando embaixo. O valor relativo desse sete aqui é 700.000. 1000. Tá bom? Tem aqui o sete, mas na verdade você tem que imaginar aqui esses cinco zeros para tu ver que ele ele é um 700.000, por isso que é 1.700.000, tá bom? Então ele é o 700.000 e desse sete o valor relativo dele, na verdade é 70.000, tá bom? Qual é o valor relativo desse 6? 6.000. Qual o valor relativo desse 5? É um 500 aqui escondido. Qual o valor relativo desse 9? Parece um 9,
mas na verdade é um 90. E o do 4 é o próprio 4.770.000 776.000, né? Então aqui, ó, 776.000 1594, tá bom? Então é isso, tá? Agora a gente vai aprofundar nessa noção, tá bom? Então isso aqui a gente pegou agora, a gente se familiarizou. Depois que a gente domina a noção de valor absoluto e valor relativo, a gente tem que dominar a noção de ordens e classes, tá bom? O que são ordens e classes? Primeira coisa, o que que são ordens, tá bom? Quando você olha para um número, vamos pegar como exemplo aqui o
836, tá bom? Você tem que entender que, por exemplo, qual a explicação? Me me diz a explicação assim, olha, por que que aqui eu tenho 74 e aqui eu tenho 47? Eles são números formados por dois algarismos e são formados inclusive pelos mesmos algarismos, pelo sete e pelo quatro. Aqui também tem o sete e o quatro. Qual é a única diferença entre eles? É só você me responder. A diferença não é a ordem. Acabou. Você já aprendeu. A diferença é a ordem. Então, ou seja, é um, são os mesmos algarismos, mas esse aqui é maior.
Esse número em geral é maior, tá? Por quê? Porque o sistema de numeração funciona assim, ó. Quando você tem apenas um número, vamos supor, eu tenho aqui apenas um número, o número oito. Esse número ele pertence a ordem das unidades. O que que é unidade? Unidade é uma coisa. Então, unidade é o que eu já quero que você pense na filosofia da matemática. Pensa agora na palavra unidade. O que que é unidade? Unidade não é uma coisa. Então, por exemplo, uma unidade de caneta, né? Uma unidade de caderno, uma unidade de estetoscópio. Muitos aqui vão
usar um dia, muitos aqui vão ser médicos. Tá? Uma unidade de camisa. Então, se eu falar assim para você, olha só, cara, oito. O que que é oito? Oito, com certeza é um, um, um, 1 um, 1 um, um, 1 um, um, 1, um, um, um. Eh, são oito o quê? Oito unidades. Eu tenho aqui uma unidade, 2 3 4 5 6 7 8. Eu tenho oito unidades, tá bom? Então, qualquer algarismo que esteja sozinho, ele com certeza representa as unidades. Só que o que que acontece, eu quero que você me responda agora. O que
acontece no momento que eu tenho, vamos lá, uma unidade, 2 7 unidades, 8 unidades, 9 unidades, 10 unidades. No momento que eu junto 10 unidades, eu posso aglomerá-las, eu posso passá-las a chamar de uma outra coisa. Na hora que eu juntei 10 unidades, eu posso dar um outro nome para elas que vai fazer com que minha minhas mãos fiquem todas livres, tá? O nome disso que eu chamo quando eu tenho 10 unidades é dezena. Eu tenho uma dezena, tá? É impressionante como que esses conceitos aqui, eu não conheço nenhum curso no Brasil inteiro que explique
isso. Ninguém explica isso. Isso é bizarro. E isso é realmente muito, muito, muito importante. Isso é fundamental. Você nunca vai ser um profissional em matemática, um aluno altíssimo nível em matemática. Quando você olha os alunos que tiram 45 em matemática no Enem, são sempre os alunos o quê? Que fizeram OBMAP, que estão a vida inteira com isso. E esses alunos, eles sempre tiveram um ensino fundamental alucinadamente forte. alucinadamente, essa é a marca de um aluno de altíssimo nível. Ele teve um ensino fundamental muito brutal. E o ensino fundamental onde isso aqui foi amplamente trabalhado em
todos os níveis, tá bom? Então, vamos lá. Eh, qualquer escola boa trabalha isso aqui muito, tá? Então, eh, o que eu tava dizendo, quando você junta 10 unidades, você pula para uma dezena, tá? E você vai ver que o que vai acontecer. Eu tenho aqui, ó, vamos contando comigo. 1 2 3. Quando eu chego no nove e eu boto mais um, o que que eu tenho? Eu tenho agora 10. Você viu que obrigatoriamente agora eu não tenho mais apenas aquela casinha das unidades. Agora surgiu o quê? A casa das dezenas. Ou seja, a casa das
Olha para esse número aqui, ele tem um zero. O o zero não vale nada. O zero ele é uma coisa nula. E quantas unidades tem nesse número? Ué, unidade aqui parece que tem zero, tá? Mas e esse um aqui? É uma dezena. É isso mesmo, é uma dezena. E o que que acontece agora? Se eu for juntando e eu tenho 10 aqui, aí agora eu junto mais nove. Eu tenho, eu tinha 10, agora eu botei mais nove coisas. Eu vou ter 19 coisas. Quando você olha pro número 19, o que que é o número 19?
Ó, aqui é a casa das unidades e aqui é a casa das dezenas. Ou seja, olha que coisa linda de você ver número 19, tá? Ele é feito pelo algarismo nove, mas o algarismo nove tá onde? Nas unidades. Ou seja, eu tenho nove unidades. Mas além de eu ter nove unidades, eu tenho o quê? Uma única dezena completa. Eu tenho uma dezena completa. Então aqui, ó, uma na no lugar das dezenas eu tenho um. Eu tenho uma dezena completa e nove unidades. Eu tenho 19. Tá conseguindo visualizar? Se eu colocar agora aqui mais uma unidade,
coloquei mais uma, eu vou ter 20, né? E como é que você escreve o número 20? O número 20, você escreve assim, ó. 20. Ou seja, nenhuma unidade, porém duas dezenas. Ou seja, tenho 20. Se eu botar mais um aqui agora, se eu botar mais três, por exemplo, 23. O que que é o número 23? Eu tenho três unidades, mas eu tenho duas dezenas completas, tá? Então, duas dezenas completas são 20 coisas e eu ainda tenho três. Então, no total, eu tenho 23 coisas, tá bom? Quando eu leio tudo junto, eu estou sempre lendo a
quantidade de unidades. Então aqui, ó, eu tenho 23 unidades, mas se eu quiser separar, eu tenho três unidades apenas e duas dezenas, mas tudo junto, né? Eu tenho 23 unidades. Beleza? Isso são as ordens. Beleza? Isso são as ordens. Então, por exemplo, olha agora. E quando eu e quando eu juntar assim, ó, 10 dezenas mais 10 dezenas mais 10 dezenas mais 10 dezenas, aí eu chegar em 90. Chegar, por exemplo, 95. Vamos lá. Tô com 95. O que que quer dizer o 95? Eu já tô aqui, ó, sempre de sempre du, tá bom? U aqui
e D aqui. Eu tenho cinco unidades, mas eu tenho nove dezenas inteiras, tá? Cinco unidades, porém nove dezenas. Tenho 95. E se agora eu colocar aqui mais quatro, então eu vou ter 99. Olha que loucura. Só que tem um problema. Você lembra que o nosso sistema decimal ele só vai até o algarismo nove? Depois dove vem o zero. Ou seja, o nove é o máximo. O problema é esse, entendeu? Quais algarismos a gente tem no nosso sistema decimal? 1 2 3 4 5 6 7 8 9. E o nove é o máximo. Depois vem o
zero, que não significa nada. Então, e agora que eu tô com 99 coisas, tá tudo bem, você tem nove unidades e tem nove dezenas, você tem 99, tá? Mas e se eu adicionar mais uma coisa, como que eu poderia expressar isso? Se eu quiser colocar aqui, ó, mais uma coisa, não tem como. Quando você coloca mais uma coisa, você é obrigado a utilizar uma outra ordem. Você lembra que tu tinha nove aqui e nove aqui? Você zera aqui, zera aqui, porque tudo agora foi aglomerado. Por que que você não tem mais? Não é que você
perdeu, é que tudo agora está aglomerado numa nova ordem. Tu tem, então, vamos dizer, uma centena. Acabou. Aí isso pode parecer, pode parecer ainda deve ter gente, eu tô fazendo questão porque essa aqui é a primeira aula da plataforma, então tô fazendo questão de explicar bem explicado, né? Ainda pode parecer que isso aqui é uma coisa boba, mas isso aqui é obrigatório para tu entender conversão de unidades. Tem um monte de gente que faz, só faz conversão de unidades com tabelinha, com uma macetinho, não entende a fluidez da conversão de unidades, tá? Então vamos lá.
Tu tem agora 100 coisas. Agora é óbvio, se tu botar mais uma coisa, tu vai ter o quê? 101 coisa. Então aqui, ó, 101. Então tu tem aqui, ó, uma centena. Eu te pergunto, quantas centenas você tem aqui? Uma. Eu tenho uma centena. E eu tenho também uma unidade. Beleza? Perfeito. Coloquei aqui agora nove coisas. Eu tenho 109, ou seja, eu tenho o quê? Nove unidades. Nenhuma dezena completa, né? Eu tenho nove unidades, nenhuma dezena completa, mas eu tenho uma centena, então tenho 109. Se eu botar mais um aqui agora, esse aqui já estoura. Quando
ele estoura, ele vira um zero. Eu sou obrigado a juntar aquele 9 + 1 que eu tinha aqui como uma dezena. Então agora eu tenho 110. Eu tenho uma centena e uma dezena, que é o próprio 110. Beleza? E Pedro? E se eu juntar agora, se eu começar, se eu tiver esse número aqui, ó, pensa aqui. Vamos apagar tudo, Pedro. Pensa no número que eu tenho aqui, que é, vamos imaginar que eu cheguei no 199. Olha isso. Cheguei no 199. Então, quais são as ordens, ó? C, D, U. Unidade, dezena e centena. Essas são as
ordens, tá bom? Ótimo. Tá? Então, tenho aqui o 199. Nesse momento eu vou pingar mais uma unidade aqui, mas ela não consegue caber aqui, porque quando eu pingo uma unidade aqui, eu junto 10 unidades. E quando eu junto 10, quando eu, olha só, quando eu junto, eu vou te dar uma regra aqui agora. Quando eu junto 10 coisas de uma ordem, eu sou obrigado. Grava isso agora. Escreva isso aí nos comentários da plataforma. Você tá assistindo pela plataforma, você pode escrever aqui embaixo. Quando eu escrevo no seu caderno, quando eu junto 10 coisas em uma
ordem, 10 coisas em uma ordem, eu sou obrigado a passar pra próxima ordem. Quando eu junto 10 coisas, não tem como ter 10 coisas. O máximo que uma ordem aguenta é nove coisas. O máximo que qualquer ordem, uma ordem isso aqui, ó, unidade, dezenas, o máximo que ela aguenta são nove coisas. Se você quiser botar mais uma, vai aparecer aqui um zero e vai aparecer um a mais na próxima, tá? Se eu tivesse aqui agora com 189, então aqui, ó, estou com 189, eu adicionei mais um aqui, não tem como, ele não aguenta, ele vai
virar um zero e, na verdade, vai passar um para cá. Então, tinha oito ali, agora virou nove. Então 189 é óbvio intuitivo. 189 virou 190. Se eu tiver agora já aqui com 199 e botar mais um aqui, o que que vai acontecer quando eu botar mais um? Esse aqui não aguenta. Ele vai virar um zero. Só que ele não aguenta e faz o quê? Ele passa pro próximo. Só que quando ele passa pro próximo, o próximo também não aguenta. Você entendeu? O próximo também não aguenta. Então eu botei aqui, eu só pinguei mais uma unidade
aqui no final, tá? Mas ele não tem espaço, ele vai virar um zero, vai passar pro próximo. Mas esse aqui também não aguenta. Então esse aqui é que vai ter que mudar. Porque agora eu acabei de fazer o quê? Eu acabei de juntar 10 tanto aqui quanto aqui. Então eu vou passar pro próximo, tá bom? Então, ou seja, eu tô e eu tô enchendo aqui 10 dezenas, eu vou juntar uma centena. Então, ou seja, de 199 simplesmente vai virar o 200. Beleza? Aí com 200 você vê aqui tem zero, aqui tem zero. Beleza? E se
você for seguindo, tudo que você tem aqui são o quê? Duas centenas, tá? E se você for seguindo, vamos supor que você vá seguindo e chegue um ponto em que você está no 999. É isso que eu queria chegar aqui, tá? Ã, chegamos aqui, né? Tô com 999. Eu vou pingar uma coisa a mais nesse último aqui, tá bom? Então eu quero botar mais um. A gente já sabe que quando eu fizer 999 e eu botar mais um, a gente sabe que isso vai virar o 1000. Mas agora eu vou mostrar porque que isso acontece.
Botei mais um aqui, ele passa pro próximo. Só que esse aqui também tá com nove, então ele vai fazer o quê? Passar pro próximo. Só que esse também está com nove. Então ele vai ser obrigado o quê? A passar para um próximo. Vai inaugurar aqui uma nova ordem, tá bom? Vai inaugurar uma nova ordem. Que ordem vai ser essa? Que ordem vai ser essa? Concorda que vai ser a ordem do milhar? Tá errado. Tá errado. Eu fiz isso para pegar você que tá assistindo aula aí agora, tá bom? Não é a ordem do milhar. A
gente só tem três ordens. A gente só tem centena, dezena e unidade. O nosso sistema trabalha assim. Ele só tem unidade, dezena e centena. São só essas três ordens. Você vai falar assim: "Meu Deus, né?" Então, como assim? O que vai acontecer? Então, vai passar pro próximo. Vai, vai passar pro próximo, só que adivinha? Vai voltar. Então, aqui, ó, tem CDU. Vai aparecer o Q de novo aqui? Adivinha? vai aparecer o e esse 999 vai virar o quê? O 1000. Agora você pode estar me perguntando assim: "Mas Pedro, como assim? O que que acabou de
acontecer? Isso aqui não é uma unidade. Então aqui que entra agora o sistema das classes, que é o outro sistema que tava faltando. Isso aqui é uma nova classe agora. Então essas três ordens aqui, elas são da primeira classe que é a classe simples. Então isso aqui é uma unidade simples, uma dezena simples e uma centena simples. Agora a gente tem uma unidade, mas não é uma unidade normal. Agora é uma unidade da classe milhar. É uma unidade de milhar. Ou seja, aqui é uma unidade, Pedro, uma unidade não é uma coisa só, é uma
coisa só, mas tudo que tem aqui agora, a partir de agora é milhar. Ou seja, por exemplo, é uma unidade de milhar. Milhar, para quem não sabe é 1000. Milhar é isso, né? Então, quando eu falo assim, milhares de pessoas, isso não quer dizer milhões de pessoas. Milhares de pessoas é o quê? 1000, 2000, 3.000, 4.000, alguma coisa assim. Se forem milhões de pessoas é porque o quê? São mais de 2 milhões de pessoas. Beleza? Eh, se fosse 1 milhão, só seria milhão de pessoas. Beleza? Então agora você vê que o o 999 que tava
com com todas as suas ordens cheias, né? Ordem das unidades da dezena da centena, agora tá com elas vazias. Porém ele tem aqui a ordem das unidades. Ele tem uma unidade, mas é uma unidade de quê? É uma unidade de milhar. Ele tem uma unidade de milhar. O que que é uma unidade de milhar? 1000. Uma unidade de milhar é 1000. Tá, Pedro? E se eu vier aqui e eu encher tudo? Eu vou encher tudo. Então aqui, ó, eu tô aqui agora com esse aqui e eu tô com isso aqui de novo, essa mesma situação
do 999. Quando você botar mais um aqui no final, bota mais um. Quanto é 1999 + 1 é 2000. Concorda? Então quando você faz isso, você colocou aqui mais um, passa para cá, passa para cá e passa para esse. Então aqui sumiu tudo de novo, só que agora aparece o quê? Mais uma unidade de milhar completa, tá? Então temos duas unidades de milhar, não temos 2000, é, temos só duas unidades de milhar, tá bom? duas unidades de milhar, que são 2.000, ou 2.000 unidades. Aí se você quiser falar o número inteiro, você vai falar: "São
2000 unidades de coisas". Tá bom? Que que vai acontecer se eu conseguir encher isso aqui? Então vamos supor que eu encha isso aqui. Eu boto aqui, ó. Eu consegui botar 9999. Agora eu quero pingar mais uma coisa aqui. Quero pingar mais uma coisa aqui. Quando eu pingar um aqui, isso aqui vai virar um um não tem como. Vai ter vai aparecer um zero, vai pular um pra frente. Vai pular um pra frente, vai pular um pra frente. Vai ter que aparecer o que? Essa daqui também não aguenta. Vai ter que aparecer uma nova ordem. Que
é qual ordem? Agora você deve estar imaginando. É a ordem das dezenas, tá? Porque lembra que eu te falei aqui, ó? É CDU, CDU e depois de novo CDU. É sempre CDU. Só que agora, lembra que eu te falei, olha só, o sistema para você gravar o seguinte, ó. Cada três ordens, três ordens elas fecham uma classe, tá? Então, essas primeiras três ordens aqui, elas são de uma classe. Agora que eu já tô, que eu além de já ter enchido elas, eu já enchi também a ordem das unidades da classe de milhar, porque aqui, ó,
isso aqui agora são as as três ordens da próxima classe de milhar. Agora que eu tô que eu já enchi aqui a unidade, eu vou ter que inaugurar a dezena de milhar. Tá bom? Como é que vai ser isso? Botei mais um ali. 9999 mais 1 vir o quê? 10.000. Como é que a gente escreve o 10.000? A gente escreve assim, ó. 10.000. Como que você pode dizer isso aqui, ó? Eu posso falar assim, ó. Eu tenho apenas uma dezena. Mas pera aí, não é não é só isso. Você não pode dizer que você tem
uma dezena. Eu sei que você tem uma dezena, tá na ordem da dezena. O restante é zero, não vale nada. Tá na ordem da dezena. Quer dizer, não vale nada assim. E nessa análise, né? Eu tenho nenhuma unidade aqui, nenhuma, eh, dezena, nenhuma centena, nenhuma unidade de milhar, eu tenho apenas uma dezena. Mas é uma dezena de quê? É uma dezena de milhar. Ou seja, uma dezena de milhar já valem 10.000 unidades de cara, tá? E agora se eu começar a encher isso aqui de novo, vou encher, vou encher, vou ter 10.000. conseguir encher isso
aqui tudo. Então agora, como é que encher? Eu tô com nove aqui, tô com nove aqui, tô com nove aqui, tô com nove aqui e tô com nove aqui. Eu estou com 99.999 coisas. Ou seja, eu tenho nove unidades, nove dezenas, nove centenas. Eu tenho nove unidades de milhar e tenho também nove dezenas de milhar, tá? Nove dezenas de milhar. Eu tenho 90.000 + 9.000 mais e 900 + 90 e mais 9. Aí eu pingo mais um aqui, vai virar o 100.000. O que que é o 100.000? Ele passa também pra próxima ordem, tá? Então
aqui eu tenho aqui agora, ó, eu tenho aqui, ó, 1 0 0 100.000. Ou seja, eu posso dizer que eu tenho aqui uma centena, mas não é qualquer centena, é uma centena de milhar, tá? Enchi isso aqui de novo. Então agora eu consegui encher isso aqui de novo. Bota todo mundo com nove aqui. Eu estou agora com R$ 999.999. Botei mais R$ 1 aqui. E agora quando eu botar mais R$ 1 aqui, ele vai ele vai encher isso aqui que não vai aguentar. Vai passar para cá, para cá, para cá, para cá. E aí, o
que que vai acontecer? Tem que passar para outra coisa. Mas lembra, já fechou aqui outro CDU. Já fechou um CDU. Então tem que inaugurar um novo CDU aqui. Tem que aparecer aqui um novo CDU. É óbvio. Imediatamente só precisa aparecer um U. Não precisa aparecer um CDU. Só precisa aparecer um novo U. Aqui é CDU. Mas não necessariamente tem que ter todos. Ó, já vou avisar. Eh, essas últimas podem estar incompletas, tá bom? Não pode estar incompletas sempre as primeiras. Você começa da direita pra esquerda. Então aqui pode ter só uma unidade. O que que
vai acontecer quando eu botar mais um aqui? Todo mundo aqui vai virar zero. Quando todo mundo aqui virar zero, é porque todo mundo passou o quê? Passou para cá. Eu tenho o quê? uma unidade. Porém, porém, porém é uma unidade. Só que olha só, lembra que a cada três ordens você fecha uma classe? Lembra disso? A cada três ordens eu fecho uma classe, né? Então aqui, ó, três ordens, que classe é essa aqui? Classe simples. Três ordens. Que classe é essa daqui? É a classe do milhar. Tudo aqui é milhar. Aqui é unidade de milhar,
dezena de milhar e é centena de milhar. Essa aqui é a nova classe do milhão. Essa é a classe do milhão. Ou seja, tu tem uma unidade, mas é uma unidade de milhão. É 1 milhão. Você entendeu? Entendeu? Se você conseguisse agora, né, encher tudo isso aqui, você teria o quê? Você teria 9.900.000999.999. Se você pinga mais um aqui agora, você satura isso aqui tudo. Tudo isso aqui é obrigado a passar pra próxima. E agora você tem o quê? Lembra? É CDU. Então agora você tem aqui de novo o quê? Um D, né? E vai
ter aqui um C. Depois agora você foi obrigado a passar para cá, ó. Um. Aí com zero aqui. 0 0 0 0 0. Ou seja, você tem o quê? Tu não tem nenhuma unidade de milhão. Tu tem apenas uma dezena, mas é uma dezena de milhão. Tu tem uma dezena de milhão, tu tem 10 milhões. Se tu satura isso aqui tudo, você tem aqui, ó, 99.999.000. R$ 999. Você bota mais um aqui. O que que acontece quando você bota mais um aqui? Quando você bota mais um aqui, você pula pro próximo nível. E agora você
tem aqui um e zero em todo mundo. Você tem o qu? Apenas uma centena. Eu só tenho uma centena, mas uma centena de quê? Uma centena de milhão. Se você encher isso aqui tudo, então você tem 100 milhões. 100 milhões. Se você conseguir encher isso aqui tudo, você vai ter o quê? 999 milhões. 999.000 R999. E você enche isso aqui tudo. Você vai ter que novamente inaugurar uma nova ordem, uma nova ordem que é a das unidades. Mas você também acabou de fechar mais três ordens. E a cada três ordens a gente tem uma classe.
Então aqui é classe simples, aqui é a classe do milhar, aqui é a classe do milhão. E agora você vai chegar na classe do bilhão. Tudo aqui é bilhão. É unidade de bilhão, é dezena de bilhão e centena de bilhão. Tá bom? Então agora o que que vai acontecer? Você vem para cá e tu vai ter apenas aqui, ó, um. Tudo que eu eu posso resumir tudo que eu tenho como um. 0 0 0. Uma unidade. Uma unidade de quê? De bilhão. Acabou. Acabou. É isso. Uma unidade de bilhão. Como que você lê qualquer número
agora que vem isso aqui? Que realmente já na primeira aula da plataforma, já quero que você saia daqui já com uma aplicação disso aqui no Enem. Como que você lê qualquer número? Vamos, eu vou pegar aqui um número aleatório e vou te falar, porque no Enem só aparece muito. Então aqui, ó, vamos lá. 3 7 5 4 0 1 9 8 3 2. Aparece esse número aqui. Você vai lá pro final do número e você começa a marcar de três em três ordens. Então aqui, ó, marquei um aqui, marquei um aqui, marquei um aqui. Pronto.
Agora você consegue visualizar, foi a ordem simples aqui, ó. Foi a classe simples, né? que cada três ordens é uma classe. Foi a classe do milhar, foi a classe do milhão e eu cheguei aqui na classe do bilhão. Poderia ter alguém aqui, né? Mas posso dizer que aqui tem zero, não tem nenhuma centena de bilhão aqui, tá bom? E agora sim você lê. Então você tá na classe do bilhão, mas dentro, lembra que eu falei que a classe mais da esquerda pode ficar incompleta? A classe do bilhão, ela tá incompleta. Aqui eu tenho sempre que
tá completo no CDU. Aqui eu tenho sempre que tá completo no CDU. Aqui eu tenho sempre que tá completo no CDU. Mas aqui eu só tenho o du. Eu não tenho nenhuma centena de bilhão. Não tenho. Eu tenho apenas três dezenas de bilhão, no caso. Vamos ler isso aqui, então, ó. 37 bilhões, 540 milhões, 19.832. Esse é o número. A gente escreveria ele bonitinho assim, ó. 37 bilhões, 540 milhões, R.32 ou qualquer coisa assim, tá? É assim que você lê qualquer número, tá bom? E a gente acaba de dominar aqui o conceito de ordens e
classes. E eu já falei também do conceito de fechar 10, que a gente também já dominou, mas eu quero que você entenda que isso aqui se manifesta em toda a matemática. Então eu quero que você pense agora, por exemplo, em questão de quantidades. Eu quero que você pense assim, ó, eu tenho aqui 100 g de uma certa coisa. Vamos supor agora que eu tenho aqui, ó, 999 g. Eu vou jogar mais 1 g aqui, tá? Eu vou jogar mais 1 g aqui. Eu vou ter o quê? 1000 g. Quando eu jogo isso aqui, eu tenho
agora aqui, ó, 1000 g. Você percebe que mais uma vez eu saí da estrutura de três ordens e eu abri uma nova. Se você quiser pegar esses 1000 g e chamar, na verdade, esses 1000 g de apenas 1 kg, tu pode. Kilograma é isso, já é o nome que a gente dá dentro quando a gente tá falando de grama. O kilograma seria o nome que a gente dá quando a gente já conseguiu aglomerar ali e 1000 da unidade da classe inferior a ele, tá? Então você vê que é justamente a mesma coisa, tá bom? Isso
aqui é realmente muito muito muito importante. E é isso, tá bom? Para fechar essa aula aqui, eu vou vir aqui agora, né? Eh, a gente aqui na plataforma S a gente sempre vai buscar fazer as aulas assim com uma duração de 40, 45 minutos. Então, vou terminar essa daqui, você já passa pra próxima. Mas olha só, isso aqui é um exercício muito simples, mas muito fundamental. O exercício é o seguinte, ó. Escreva o número de classes, o número de ordens e o número por extenso, tá? Eu ainda botei aqui na apostila, né? Confia em mim.
Isso realmente vai te ajudar na prova do Enem. Todo ano cai uma questão que exige esse tipo de leitura e muita gente boa erra. Então eu dei até aqui o exemplo, né? Quando tu olhar o o 1324, você vai dizer assim, ó, ele tem quatro ordens, né? Porque ordem é cada posiçãozinha aqui, tá bom? Quatro ordens. Tem duas classes, né? Porque ele tem a classe simples e ele tem já a abertura da classe de milhar, tá bom? Ele tem uma unidade de milhar e aí escreve o número 1324, tá? Eu vou fazer aqui com vocês
pra gente treinar isso, beleza? Então vamos lá. Esse aqui primeiro vamos colocar nele o número de ordens e o número de classes, tá bom? Então esse aqui primeiro eu vou colocar assim a a letra vou vou abreviar, tá bom? Ele tem o quê? Três ordens e tem o quê? Apenas uma classe. Somente a classe simples tá aberta nele, tá bom? Ele é o 387. Em vez de eu escrever aqui, eu vou falar para você, para você conferir no seu gabarito. Esse número aqui, quem é? Eu venho daqui para cá, eu fecho aqui o três, tá
bom? E vamos lá. Eu tenho aqui cinco ordens, né? Porque ele tem cinco posições, são cinco ordens, tá? Então, cinco ordens e ele tem duas classes, tá bom? Ele tem a classe simples e ele tem também a classe do milhar aberto. Então, ele tem cinco ordens e duas classes. Beleza? Sensacional. Que número é esse aqui? Ele é o 28.000. Essa aqui é a parte que tá dentro da classe do milhar, você concorda? Então, ele é o 28.904. Acabou. E esse número aqui, que número é esse? Vamos marcar aqui três coisas e três coisas, tá bom?
Ele tem seis ordens. Tem seis ordens e tem duas classes fechadinhas, tá bom? Então aqui, ó, duas classes, tá bom? São aqui, ó, uma é uma centena de milhar, são quatro dezenas de milhar, cinco unidades de milhar, 145.568, tá bom? Com cinco centenas, seis dezenas e oito unidades. Beleza? Show. Que número é esse aqui? Vamos dar uma olhada quantas ordens ele tem. 1 2 3 4 5 6 7. Ele tem sete ordens. Perfeito. Então, tem sete ordens. E quantas classes ele tem aqui, ó? Uma classe, duas classes e, ó, três classes. Esse 0 não muda
nada, tá bom? Isso aqui é uma classe de milhar completa, tá bom? É porque isoladamente ele não tem nenhum milhar completo. Como assim não tem nenhum milhar completo? É, ele tinha 999, mas aí aconteceu alguma coisa que ele fez 1 milhão e depois de fazer 1 milhão, ele começou de novo a encher lá do final, mas ele ainda não encheu o suficiente para vir alguém para cá, tá bom? Então quem tava aqui já passou para esse aqui, tá? Então são sete ordens e o quê? Três classes. Que número é esse? A gente tem aqui, ó,
apenas uma unidade de milhão, tá? Uma unidade de milhão. Então a gente tem o quê? R 1.123. Eu tenho R$ 1.123 ou qualquer coisa assim. Tá? E esse número aqui, não se engane, tá? Esses zeros à esquerda, eles não têm valor algum aqui nesse caso, tá bom? Esse zero aqui não vale nada, tá? Eh, então assim, não não caia nessa, tá bom? Isso aqui realmente é um número que só tem duas ordens. Eu botei aqui intencionalmente, tá bom? Ele tem só duas ordens, tá bom? Ele só tem aqui o dois e um. Zero à esquerda
não tem valor algum. Zero à esquerda não muda nada. O zero ele tem que aparecer na direita empurrando os números para trás, tá bom? Então ele tem duas ordens e ele tem apenas uma classe, tá bom? Porque na verdade esse número aqui ele é o 12. Esse número não é o 0 0 12. 0 12 é o 12, tá? Então é só um 12 mesmo. Aqui não tem nada além disso. Eu só botei o 0 0 para confundir vocês, tá bom? É diferente desse tanto de zero que eles todos estão à direita desse número um.
Então eles forçaram esse um para trás, tá bom? Então no caso aqui eles têm valor sim, eles estão aqui dentro, eles têm total valor, tá bom? Você acha que se você deve isso aqui ao banco? Vamos supor que você deve isso aqui ao banco, ó. Eu devo 0 12 ao banco. Se você pagar 12, eles vão estar satisfeitos. Agora, tu acha que se tu deve isso aqui ao banco, tu pode falar assim, ó, o zero não tem valor. Eu vou pagar só isso aqui, ó. 13.456. Claro que não, você vai ser preso, tá? Então, quantas
ordens tem ele aqui, ó? 1 2 3 4 5 6 7 8 9 10 ordens, tá? Isso aqui é um número de 10 ordens. E quantas classes ele tem? Não sei. Vamos ver. Aqui eu tenho três ordens, fechei uma classe. Aqui eu tenho três ordens, fechei uma classe. Aqui eu tenho três ordens, fechei uma classe, que é a classe inclusive aqui do milhão. Aqui é a classe simples, classe do milhar, classe do milhão. E eu tenho uma unidadezinha que essa uma unidadezinha, ela já está na classe do bilhão. Então são quatro, são quatro classes, tá?
Que número é esse? 1 bilhão. Não tem nenhum bilhão aqui separado. É 1 bilhão. Que é óbvio que esse 1 bilhão ele veio de 999 milhões mais 1 milhão, tá? 1 bilhão, não é? 1 bilhão. Todo mundo concorda que 1 bilhão é a mesma coisa que 1000 milhões. 1 bilhão você tem quando você junta 1000 milhões. Pedro, mas então por que que a gente não fala 1000 milhões? É porque a gente, o nosso sistema é isso. Quando a gente junta, eh, quando a, você lembra que eu falei para você assim, ó, quando a gente junta
10 coisas, a gente passa de ordem. Lembra disso? Eu falei, isso é uma regra. Quando a gente junta 10 coisas, a gente passa de ordem. E quando a gente junta 1000 coisas, a gente passa de classe. Quando você junta 1000 coisas, quando não não necessariamente 1000 coisas, quando você junta eh quando você fecha três ordens, quando você fecha ali, é realmente 1000 coisas, quando você fecha 1000 de uma certa eh 1000 coisas de uma certa classe, você vai pra próxima classe, tá bom? Então, na classe do milhão, essa classe do milhão, ela aguenta e 999.
Se você fechar e você botar 1000 milhões, você até pode falar 1000 milhões, mas a gente vai dizer o quê? O jeito certo é falar o quê? 1 bilhão. 1 bilhão já resume a história toda, tá bom? Então esse número aqui é o quê? É 1 bilhão 3456. É um número que muitas vezes as pessoas teriam dificuldade de falar, tá? Mas esse número o quê? 1 bilhão, ele não tem nenhum milhão. E dentro da classe dos milhares ele não tem centena, não tem. Ele só tem o quê? 3.000. Então se não fosse o restante aqui,
seria o quê? R456. Então é isso que você tem. R$ 1.3.456. Pô, fala sério. Se você para para pensar, você vai ver que muita gente não saberia dizer que número é esse, tá? E esse número aqui, vamos lá. Fechou aqui três ordens. Eu chamo isso de uma classe. Fechou três ordens de novo. Fechou três ordens. Mais uma vez eu tenho uma unidade de bilhão. Então eu tenho aqui o quê? 10 ordens e quatro classes. Mesma resposta de cima. Vamos lá. 1 bilhão. 10 milhões. Ó, 1 bilhão. Aí na classe dos milhões tem só essa essa
uma dezena de de milhão. Então 1 bilhão 10.44.589, né? Perfeito. 1.1.44.589. Esse é um número. É assim que se fala esse número. Às vezes na sua vida você não saberia dizer esse número. Você ia ficar todo enrolado. Tem que saber dizer esse número. Tá show? Vamos lá. E que que é isso aqui? Vamos lá. Vamos. A gente sempre começa e vai fechando de três em três, entendeu? Vocês dev, quem quem tá assistindo aula agora deve ter percebido que quando você viu a teoria já tinha entendido, mas é no exercício mesmo que a gente realmente fixa.
Por isso que esse ano eu trouxe só na primeira semana aqui da plataforma 250 exercícios, que a gente vai fazer exercício para caramba e a gente vai chegar nos exercícios do Enem, inclusive, mas a gente vai, ó, dessa vez você vai realmente fixar tudo na base dos exercícios, tá bom? Então vamos continuar aqui esse aqui. Vamos lá. A gente tem aqui três, beleza? Vamos contar aqui. Três ordens, seis ordens, nove ordens com mais 3, 12. Temos 13 ordens nesse número, tá bom? Temos 13 posições. E quantas classes nós temos? Vamos lá. Então, aqui, ó, uma
classe, duas classes, três, qu cco classes. Legal. Mas que número é esse? Então, a gente já saturou aqui várias vezes a classe completa do bilhão e a gente foi obrigado a juntar aqui uma nova classe que eu não tinha mostrado na teoria, mas é a classe do trilhão. Aqui a gente tem o quê? Apenas quatro unidades de trilhão, tá? A gente tem quatro unidades de trilhão, tá bom? quatro unidades de trilhão, beleza? Então, pronto, quatro unidades de trilhão, tá? Eh, só para quem tá perguntando assim, ó, essa pergunta pode surgir sobre reais. Se isso aqui
fosse em reais, eu deveria colocar vírgula que não. A vírgula nos reais se coloca justamente depois que você acabou já o número normal. Se tu quer falar isso aqui em reais, tu vai dizer o qu, ó, 1 bilhão 10.44.589. Se quiser, tu bota o vír00 para dizer que não tem centavos ali quebrados, tá bom? Aí tu bota aqui o RS e acabou, tá bom? Então é, é tudo com ponto mesmo. A gente usa o ponto para separar. Nos Estados Unidos aqui o ponto é uma vírgula, o ponto vale vírgula, mas aqui é ponto mesmo, tá
bom? Então vamos lá. Eu tenho 4 trilhões. Vamos lá. Eu tenho 4 trilhões. Aí lembra aqui tem tudo CDU, tá bom? Então tem cinco centenas de bilhão com cinco dezenas de bilhão com oito unidades de bilhão. Beleza? Vamos nessa. Eu tenho aqui, ó, o número é 4 trilhões 558 bilhões. Então você vê, você sempre lê dentro de uma classe, você sempre dentro de uma classe, você sempre lê o número completo. Você dentro de uma classe, você não para, você fala o que tá na sua frente. 558. É, esse é o número? Sim. 558 e o
nome da classe. Então vamos lá. 4 trilhões, 558 bilhões, 694 milhões, 838.000. A gente só não fala só a classe dos milhares que a gente não fala geralmente 838.000. milhares. A gente fala 838.000. Então vamos de novo para todo mundo fixar. 4 trilhões 558 bilhões 694. R838.920 ou qualquer coisa. Beleza? É isso. Mais uma vez fechamos aqui. OK. Perfeito. Foi. Tá. Então espero que tenha dado para entender e eu vou encerrar essa primeira aula por aqui. Se você e tá aí agora logado na plataforma SAD, né? Claro que tá. que você tá assistindo essa aula,
eu sugiro fortemente que se você puder você já parta pra próxima, porque na próxima agora a gente vai começar a acelerar o ritmo, tá bom? Então, parabéns a todos que assistiram essa aula. Até a próxima e, opa, parabéns, você concluiu aí a primeira etapa da aula, né? Já sabe agora sistema de numeração decimal, gostou? Ordem, valor relativo, valor absoluto, classes, sabe tudo isso. Agora a gente vai entrar de fato nas operações subtração, soma, multiplicação e divisão. Mas eu já aviso, aqui não é o meu curso de cálculo mental. Então, tem aqui no YouTube gratuito o
meu curso de cálculo mental. Lá eu explico como, explico muito, né? fico fazendo muito com você cálculos de cabeça, coisa assim. Nessa aula aqui o foco não é esse. Então eu vou passar pelo pelos cálculos de de subtração, adição, multiplicação, divisão, mas não vou dar um enfoque tão grande quanto lá no curso. Depois dessa aula aqui, se tu quiser, tu vai lá e assiste também o curso de cálculo mental gratuito que muda a tua vida por completo. E como eu disse, tá gratuito, mas continua focado nessa aula aqui que você vai gostar do que tá
por vir. Vamos nessa. Parabéns por est conseguindo acompanhar. Tô gostando de ver. A gente agora vai ver os princípios fundamentais para que você consiga fazer qualquer operação básica, tá? E nessa aula aqui, especificamente, eu vou focar em mostrar esses princípios para as operações mentais, tá bom? Vocês vão perceber que eu peguei um trechinho aqui da apostila, né, que na nossa apostila, eu nem lembro em que página vai est isso, mas tem um momento que eu falo sobre os princípios das operações mentais, tá? Então aqui, ó, os três mecanismos da matemática mental, tá? Então esses três
mecanismos aqui são os mecanismos obrigatórios que você tem que ter conhecimento e você tem que desenvolver na sua inteligência, tá bom? Vamos lá. Mecanismo da complementariedade dos números. mecanismo de arredondar e corrigir e mecanismo da decomposição em unidades, dezenas e centenas. Tá bom? Então, como que funciona? Eu vou explicar esses três mecanismos enquanto eu explico a matéria. Eu não vou parar para explicar os mecanismos para depois eu falar outra coisa, tá? Eu vou explicar os mecanismos enquanto eu estou fazendo aqui tudo, tá bom? Então, vamos lá. Eu vou ignorar esse princípio de cálculo mental e
vou direto para adição. Só que enquanto eu falo da adição, da subtração, eu vou falar dos princípios, tá bom? Como que você deve fazer para enxergar uma um qualquer tipo de cálculo mental? Vamos supor que eu que eu diga para você assim, ó, 3 + 7. Eu tenho certeza que isso aqui é instantâneo para você. Você rapidamente enxerga que 3 + 7 já fecham 10. Ninguém tem dificuldade com isso. Por quê? Porque eles são números que se complementam formando eh fechando a ordem deles, tá? Números que se complementam fechando uma ordem são muito fáceis de
identificar. Então, por exemplo, se eu tiver 4 + 6, eu tenho certeza que para você é agradável de pensar no 4 + 6. Você consegue imaginar o encaixe do 4 + 6. Se eu falar 8 + 2, é bem agradável de pensar também. 8 + 2 você consegue facilmente, ó, encaixar. Se eu falar é quanto é 14 + 6, mesma coisa, você enxerga que é 20, porque de novo é o 4 + 6. A única diferença é que a gente já tem aqui uma dezena fechada, mas essa dezena fechada agora a gente juntou essas unidades
aqui, fechou outra dezena, a gente tem ali o 20 certinho. Beleza? Ótimo. Se eu falar para você assim, quanto é 34 + 16, também não tem mistério, né? Porque você tem aqui três dezenas e aqui você tem outra dezena, você teria quatro dezenas, mas além de ter quatro dezenas, né? Três dezenas e uma dezena são quatro, tu ainda tem aqui o 4 + 6 fechando 1 qu. Então você tem exatamente aqui, ó, 50 unidades, tá? ou cinco dezenas, se você preferir, tá? Essa é a complementariedade dos números e ela é fundamental. Mas é óbvio, você
pode pensar assim: "Mas Pedro, isso aí não só funciona para esse caso?" Claro que não. A complementaridade ela funciona tanto quando o número é complementar quanto quando ele não é. Isso é um mecanismo mental que você tem que ter. Como assim, Pedro? Não entendi. Funciona até quando ele não é Funciona até quando ele não é complementar. É, por exemplo, se eu tiver assim, ó, 7 + 4, você concorda que eles não são complementares? Não são. Só que para você fazer essa soma mentalmente, você vai ter que imaginar o sete e aí desse quatro você adiciona
apenas o três nele, fecha 10 e ainda vai sobrar um. E aí tu vai pro 11, tá? Quando você pensar, por exemplo, em fazer 18 + 6, você tem que primeiro encaixar aqui, ó. Como é que você coloca um 6 dentro de um 18? Você concorda que você precisa colocar primeiro um do e você enxerga que tem que ser um dois para fechar o 20. Quando você coloca um dois e fecha o 20, ainda sobra quatro aqui. E você sabe que a resposta é 24. Se eu falar 24 + 7, você tem que botar o
7 dentro do 24. Mas primeiro você bota um 6, fecha 30. E agora você botou um seis, ainda tem um, vira o 31. Entendeu? Ou seja, você tá usando a complementaridade do mesmo jeito. Mesmo quando a complementaridade não fecha certinha, você tá justo, você precisa dela para perceber que fechou e tem um excedente que tem que ser adicionado. Como é que você vai fazer de cabeça a soma? Se eu falar para você assim, ó, quanto é 78 + 6? Você precisa primeiro botar dois, mas é rápido, é automático. 78 + 6, você encaixa dois, fechou
80, ainda tem quatro, você fecha aqui 84. Quanto é 84 + 8? Você pega aqui, coloca o oito aqui. Mas como que você coloca o oito dentro do 84? Você vai botar o seis primeiro, vai fechar o 90 e ainda tem dois. Porque do oito tu só botou seis, porque tu já sabe que o quatro pede um seis. O quatro pede um seis para fechar ali. Então entrou ali o seis, só que tu ainda tem dois aqui, fica 92. Beleza? Esse é o mecanismo da complementariedade dos números. É óbvio que ele também se aplica não
apenas às unidades, né? Então ele se aplica tudo. Se eu falar para você assim, ó, quanto que é 80 + 20? Não é bem fácil e agradável de perceber que isso aqui é 100? Quanto que é 800 + 200? Não é bem fácil e agradável de perceber que isso aqui é 1000? Concorda? Agora, se eu falar para você assim, ó, quanto é 810 + 240, você concorda que o primeiro mecanismo é você visualizar 810 + 240, como na verdade eu vou somar apenas o 800 mais o 200, só o 800 mais o 200 já dá
1000. Agora que eu já fechei esse 1000, eu ainda tenho aqui 10,40 que dá 50. Então é 150. Tá percebendo? Tá sacando? Tá conseguindo visualizar? Então você vê que a complementaridade está realmente obrigatoriamente presente em qualquer tipo de cálculo que você vá fazer. Qualquer tipo de cálculo mental pede que você entenda essa estrutura de olha, você primeiro tem que fechar o que você pode fechar e o que sobra você apenas vai colocar que sobrou. Por exemplo, se eu tiver aqui, ó, 784 + 36, como que você vai fazer isso? Você vai pegar desse 784 aqui,
você vai olhar pro 36, você vai tirar 16 e colocar aqui para preencher o 800. Então aqui, ó, tu tira 16 e bota aqui, tu vai fechar exatamente 800. Mas se tu tirou 16 daqui, você não continua tendo 20 aqui. Então a resposta é 820. Ó, você tirou 16, fechou 800. Só que você tirou 16 aqui, ainda sobrou 20. 820 é a resposta. Beleza? Então a gente vai aprofundar muito, muito, muito nesse princípio da complementaridade, tá? ao longo de todas as nossas aulas aqui, essa primeira aula de cálculo mental, eu tô eh eu tô tipo
apresentando o princípio, tá bom? Agora, e o princípio de arredondar e corrigir, ele é um princípio eh que ele evita que você tenha que fazer várias complementaridades. Por exemplo, se você tivesse, você percebe que se você tivesse, assim, ó, 79 mais eh, vamos supor, 77 + 9, é claro que você pode usar a complementaridade, você pode colocar três aqui mentalmente, né? Você pode visualizar, vou colocar três para fechar um 80. E agora que eu já coloquei três aqui para fechar um 80, aqui sobrou seis, então dá 86. Mas o princípio de arredondar e corrigir é
melhor nesse caso, é mais rápido. Quando você vê um número que você vai somar com com nove, vou botar nove dentro de algum número, você na verdade coloca 10 e retira um. Porque se você quer somar nove, você vai colocar 10 e vai puxar um, você vai ter somado nove. Então quando você olhar 77 + 9, você já vai botar 10, vai virar lá o 87. Você puxa um, vai virar o 86, que é a mesma resposta. Quando você tiver eh 68 + 9, você imediatamente você bota 10, 78, puxa um, vira 77. 77 +
9 você, acabei de fazer em cima, se tu tiver aqui 63 + 9, você adiciona 10 e volta um. Então você adicionou 10, você foi lá pro 73, você voltou um, você foi pro 72. Beleza? 72 + 9, você adiciona 10, vai lá pro 82, você volta um, você vai pro 81 de novo. Tá bom? É isso. Esse é o princípio de você arredondar e corrigir. Aí como que ele funciona melhor? Se você quiser somar oito, é a mesma coisa. Você não precisa fazer a complementaridade e o excedente. Você tem aqui, ó, 134 + 8.
Você vai somar 10 e vai puxar 2, porque o 8 é isso. O 8, o 8 é justamente isso. O 8 é um 10 - 2. Eu posso trocar o 8 aqui, né, claramente por um 10 - 2, que vai ser a mesma coisa. Então, 134 + 8, tu já vai imediatamente ver o quê? 144 volta 2, 142. Tá bom? 142 + 9, tu vai avançar 10, 152. voltão 151, entendeu? Eh, e é isso, tá? Esse é o princípio da complementariedade, já falei, e agora o princípio do arredondamento com a correção. Olha como é que
esse princípio ele é universal, ele se manifesta em todas as coisas. Se você tiver aqui 7394 + 90, como que você faria isso aqui? Da mesma forma que o 9 você vai somar 10 e tirar um. O 90 você vai somar 100 e tirar 10. Que que é 90? Não é 100 - 10. Então 7394 + 90. Você já vai enxergar 7.000. 94. Só que aí agora você puxa 10. Então 7494 seria se você tivesse botado 100, mas invés de 94 você bota 7484 porque tu recuou 10. Tá percebendo isso? Realmente deixa a coisa muito,
muito, muito mais rápida, deixa a coisa muito mais ágil, tá bom? Se você tiver é 3.000 ã 400, vamos lá, 3.200 e ã e 77 + 80, como é que tu vai somar esse 80? tu vai somar 100 e vai recuar 20, tá? Então 3277 + 80, tu vai fazer 3377. Só que aí você vai recuar 20, vai virar 3357. Olha como que é obrigatório. Olha como que é obrigatório você ter a noção de ordem. Porque quando eu fui somar 100, vocês perceberam que eu someio 100 aqui? Eu falei assim, ó, 327 + 80, eu
fui somar 100. Eu botei onde? Eu botei aqui. Concorda? Eu botei assim, 3300. E quando eu fui tirar 20, eu tirei daqui, ó. Desse sete eu tirei o 20. Então, ou seja, quando eu tô tirando 20, eu tô tirando eh dezenas e quando eu tô somando 100, eu tô somando centena, tá? Então, por isso que isso tem que tá tão conectado na sua mente, por isso que você não pode ter problemas com isso, tá? Então, eh, senão você começa a ter deficiências em toda a tua matemática e você não sabe porê. Você vai tentar assistir
a aula do professor, você não vai entender e você vai falar: "Por qu, será que eu sou burro?" Às vezes é porque você tem lacunas de ensino fundamental que não foram sanadas. Se eu tiver aqui, ó, eu tenho aqui, ó, 94.340 340 + 80 eu vou somar 100 e vou tirar 20. Então vai ficar o quê? 94.000, ó, 94.440, só que 420. 94.420. Tá claro que eu também poderia fazer pela complementariedade. Como assim, ó? Tá vendo como é que eu coloco 80 aqui dentro? Você concorda que eu poderia aqui, ó, eu preciso de 60 para
fechar aqui, ó. Quando eu botar 60 aqui, ó, eu vou fechar 400. Então, aqui, ó, 94.400 porque eu botei 60. Só que se eu botei 60, faltou 20 ainda. Então, 400 e sobra o 20. Complementaridade também funciona normalmente, tá? Então não tem como você me perguntar assim: "Qual que eu devo usar?" Isso aqui automático, você vai vendo qual que você usa na prática, tá bom? E o último automaticamente a gente também ensinou que é a decomposição em unidades, dezenas, centenas. Ó, aqui o tempo todo eu tô fazendo isso quando eu precisei. Se eu falar para
você assim, ó, se eu falar para você agora assim, ó, quanto que é ã 16.435 + 90, você vai somar 100 e vai recuar 10. Só que para você somar 100, você não tem que visualizar que o 100 entra aqui, ó, tem que ficar 16.535 se tu somar 100. Só que aí para você tirar 10, você não tem que tirar daqui do 35. Então 525, tá? 16.525. Ou seja, você tem que o tempo todo saber decompor o número, tá bom? Isso tudo a gente falou aqui pra soma. Agora vocês vão ver como que os princípios
eles se aplicam nas outras operações, tá bom? Então essa aula aqui é uma aula de visão geral. Depois dessa aula vai ter aula só de adição, vai ter aula só de subtração, aula só de divisão, aula só de multiplicação, aula só de potenciação e aula só de radiciação, tá bom? Essa aula aqui ela é para fazer uma apresentação geral das coisas, tá? Então, eh, vamos lá, apresentando aqui. Não, eu vou deixar essa aula só para adição. Eu vou fazer o contrário. Eu vou fazer primeiro só uma aula de adição. Tô decidindo aqui agora, né, enquanto
tô gravando. Vou fazer uma aula primeiro só de adição. Então, agora que eu já expliquei a adição, é, é bom porque eu já posso resolver os exercícios, tá? Então, olha só, efetue as seguintes operações sem utilizar o papel apenas mentalmente, tá? Então, vamos lá. Sem utilizar o papel apenas mentalmente, tá bom? Isso aqui é justamente isso, tá? E se você for perceber, eh, você já vai ver que em todos os lugares se dá, eu acabei de perceber isso, todos os lugares se dá o quê? Uma aula para toda a matemática básica, todas as operações, tá
bom? Então é justamente essa diferença aqui. A gente vai focar em cada coisa muito detalhadamente e essa é a chave para você ter muita velocidade. A gente sabe que velocidade é o que mais tá contando na prova do Enem de matemática hoje em dia. Então vamos lá. 4 + 17. Facilmente a gente sabe que a resposta aqui é 21, tá? Pela complementaridade inclusive, né? 17 + 4 eu coloco 3, sobra mais 1, vai ficar 21. 87 + 3 é muito ridículo. A gente vê que é 90 de cara. 98 + 11 a melhor forma de
fazer, você primeiro bota uma unidade, depois bota uma dezena. Então vira 99. Quando boto uma dezena, vira o 109. Beleza? Então aqui, ó, 109, 107 + 37. Como que a gente vai fazer isso? Agora existe um outro macete que é você eh decompor o número mentalmente, né? E ao invés de você fazer 107 + 37, eu prefiro que você some primeiro 100 + 30, que dá você que dá 130. Agora o 130 com esse 77, que é o 14, dá o 144. Tá bom? Outra forma de fazer, você estabiliza o 107 na sua mente. Então
você pensa o 107. Agora que eu pensei o 107, eu adiciono nele o 30. Então 137. E agora eu boto mais um sete. Então eu já tenho 137. Quando eu tenho 137, boto mais um sete. Que acontece? Desse sete entra três para fechar o 140, sobra quatro para fechar o 144. Beleza? Então e tenta visualizar isso, tá? Tenta visualizar dessa forma que você tem aqui o 107, você botou um 30 nele, virou um 137. Agora falta o quê? Falta o sete. Como é que você coloca o sete aqui dentro? O sete ele ele dá três
unidades para fechar ali o 140 e ainda sobram quatro dele, tá bom? Essas quatro unidades que sobram do sete fazem o 144, tá? Isso tem que ser uma coisa mental. 47 + 32. Vamos colocar o 30 primeiro. Quando eu tenho 47 + 32, eu boto 30, ele vira 77, né? Até porque esse 4 + esse 3 vai pro 70. A gente tem que ter a noção de que a gente tá somando primeiro a dezena. Eu tenho 47, eu vou botar primeiro as dezenas do 32, tá bom? São três dezenas, ele vai para 77. Agora com
esse dois, ele vira o 79, tá bom? 435 + 105, estabiliza o 435, bota o 105 dentro dele. Então como que você coloca o 105 ali? Você coloca o 100, ele vai para 535. Você bota o 5, ele vai para 540, tá? Então, 540. Beleza? Agora vamos lá. 73 + 987. Eu gosto de estabilizar o número maior, tá? Então, no número maior, eu pego aqui o três, coloco aqui, eu já vejo que é um 990. Agora que eu tenho 990, eu tenho que botar 70 nele. 990 + 70, esse 70 bota 10 ali para fechar
1000 e sobra 60, fica 1060 a resposta. Beleza? 1060. Somar esses aqui agora é sempre bom você perceber qual é a soma melhor para fazer, que vai fechar as casas mais certinho, tá bom? Então, essa essa aqui, como é que funciona? Olha só. 12. A gente junta aqui porque a gente tá vendo que o 2 e o 8 eles vão fechar juntos, tá bom? Então 498 + 12. Colocou o 12 aqui, o 12 encaixa aqui, fecha o 500. Tem um 10 aqui ainda. 510. Estabiliza o 510 na sua mente e bota o 132. 510 +
132. 510 mais o 100, 610. O 32 agora entrando numa coisa que já tem 10, vira um 42. Então 642. Beleza? Tá conseguindo visualizar? Agora é claro, você poderia ter começado aqui, né? Se eu coloco dois aqui, fecho um 500 e ainda tem 130, 630. 630 com 12, você vai virar o 642, tá bom? Agora aqui, 999 + 333. Uma forma muito boa de fazer isso quando você tem números assim é você já botar o lembra do que eu falei? Arredondar e corrigir. Tá vendo esse 999? Você visualiza ele como sendo 1000 e depois você
tira um do resultado final. Então você vê o 999, você já fala assim, ó, 1333. Mas pera aí, eu botei um a mais, então é 1330 é 2. Entendeu? Então o um a mais que eu botei aqui para me facilitar, eu retiro no final. 197 + 313. Primeiro eu vou pegar aqui eh o três daqui e vou colocar aqui. Então aqui eu tenho 200 e aqui eu tenho 310, tá? Então 200 + 310 dá 510. Beleza? Agora aqui, ó, 7 + 49 + 14 é uma soma aleatória, né? Como é que eu vou fazer isso
aqui? Sei lá, eu tenho que dar um jeito de fazer, tá? Então 7 + 49 dá quanto? 56. Porque o 7 dou apenas um para fechar o 50. Sobra 6 56. No 56 agora no 56 eu vou colocar o 14. Só que olha que coisa boa. Eu tenho 56, vou botar o 14. O 4 entra fechando 60 e tem 10, fica 70. O 70 + o 30 me dá o 100. Beleza? E essa última aqui, eh, eu tenho 222 + 33 + 44. Cara, eu posso começar somando só as centenas. Só as centenas. Então aqui,
ó, tenho 200 + 300 + 400. Então aqui, ó, 200 + 300, 500 + 400 já tem 900, tá? 900. Agora você já percebe o padrão, né? Que quando você tem 2 + 3, isso dá 5 + 4, isso dá 9. Então, nas centenas você vai ter nove, nas dezenas você vai ter nove. E nas unidades você vai ter nove, tá bom? Mas se você fosse fazer e sem perceber esse padrão, 200 + 300 + 400, 900. Agora 20 + 30, 50 + 40, 90. Então 990. Agora 2 + 3 + 4 9. 999 é
a resposta. Beleza? Então fechamos aqui a nossa aula introdutória de adição, tá bom? Então isso aqui é o que você precisa saber de adição e o restante você vai pegando ao longo do curso, tá bom? Parabéns por ter assistido mais uma aula da plataforma SAD. Até a próxima. Fique no gás. Vamos junto pra próxima aula. E é isso, valeu, seja muito bem-vindo a mais uma aula da plataforma SAD. Agora a gente já tem aí os princípios de cálculo mental e eles já foram ensinados aí grudados na aula de adição. Então a gente já teve a
aula de adição, já teve também a aula de exercícios de adição, tá? E agora a gente vai pra aula de subtração. Subtração é a mesma coisa que uma diferença, tá bom? Se eu falar assim, olha, quanto é 70 - 15, a resposta disso é 55. Mas como que você tem que interpretar essa conta? Eu tô querendo saber, cara, qual é a diferença entre o número 70 e o número 15. Percebe? E por que que a gente diz a diferença? Porque você concorda que a diferença é aquilo que falta para eles serem iguais, tá? A diferença
é o que falta. Então, por exemplo, qual é a diferença entre essa caneta e essa? É, tem várias, mas se eu não tivesse, elas seriam a mesma caneta, tá? Então, quando eu falar assim, ó, a diferença entre o 70 e o 15, eu quero o primeiro menos o segundo. Não é nem isso cai muito, não é nem você tem que ter essa noção. Quando você fala assim, ó, qual a diferença entre esse termo e esse? Você tem que ter saber fazer isso, saber que é o primeiro menos o segundo. Então, quais são as formas de
você fazer adição mental? São duas, tá? Isso tá na nossa apostila aí. Quem tá aí acompanhando pela apostila vai perceber que eu falei claramente disso, ó. Eh, depois da parte de soma, eu falei aqui, ó, eh, eu falei aqui da subtração na apostila. Olha o que eu falei. Vale até a pena a gente dar uma olhada junto aqui, porque eu deixei bem explicado aqui. Olha, a subtração também pode ser chamar de diferença. Qual é a diferença entre 10 e 8? A diferença são duas unidades, concorda? Se eu fizer 10 - 8 vai dar 2. Existem
dois raciocínios básicos sobre subtração. Olha isso aqui. Ou você vai do menor número até o maior, ou você pensa no maior e remove dele o menor. Pô, olha que sensacional. A postura tá muito didática, né? Eu espero que você esteja gostando, tá bom? Olha só, se eu te perguntar quanto é 20 - 4, eu vou mostrar aqui agora para vocês, né, na com a aula teórica, tá? Eh, os dois raciocínios, tá? Para vocês verem com bastante detalhe. Se eu falar assim, quanto é 20 - 4? A primeira coisa é você pensar o seguinte, ó. Do
4 até o 20, entendeu? Então, quando eu falo de a subtração, você sempre pode pegar o maior número e tirar o pequeno. Ou você pode ir do pequeno até o número grande, tá? Então, falá, quanto é 20 - 4. Você pode fazer assim, ó. Estando no 4, quanto falta para eu atingir o 20? E aí você precisa ter a complementaridade dos números em mente. Então, olha só, eu tô no quatro, quanto falta para eu chegar ao 20? Primeiro eu preciso chegar ao 10. Concord do 4 até o 10 já tem seis. Agora que eu cheguei
ao 10 até o 20, eu sei que faltam 10, então tem 16. Do 4 até o 20, você enxerga. Primeiro até o 10 eu subo seis. Pela complementaridade eu enxergo isso. Agora que eu subo seis, eu subo mais 10. Eu tenho 16. Tá? Agora a outra forma de você pensar que eu escrevi isso na apostila, né? Estando no quatro, quanto falta para chegar até o 20? Ah, faltam 16. A resposta é 16. Primeiro eu preciso de seis, aí eu chego no 10 e depois eu preciso de mais 10. Aí eu chego no 20. Perfeito. E
aí a segunda forma é a seguinte. Você também pode pensar no 20 e remover quatro unidades dele, tá? Aí a gente tem o 20. Então você pensa no 20, né? Aqui, ó. Aí ele falei assim, aí temos o 20, tirando quatro unidades, ele cai pro 16. Então aqui a gente tem o 20. Agora é 20 - 4 a conta. Então 20 - 4. Então eu desço 4 eu vou pro 16 que também é a resposta. Então tem que dominar as duas. Mas se eu falar assim, ó, quanto agora vamos escolher qual usar, tá bom? Então
agora eu vou mostrar aqui qual que você deve utilizar, tá bom? Vamos lá. Vamos supor, se eu te perguntar quanto é 187 - 13, né? Eu gosto, tô falar aqui para você que é meu aluno, eu gosto sempre de de perceber assim, ó, quando é um número muito grande que ele vai, eu vou tirar dele um tasquinho, eu gosto de pensar no grandão e tirar o pequenininho dele, porque se tu for ver, cara, daria muito trabalho. Eu devo até ter escrito isso aqui, ó. Eu acho mais intuitivo pensar no 187 e tirar o 13 dele.
Lembra aqui, ó. Então, eu tenho 187, ó, tira três, ele vai para 184. Então 187, tirei três, foi para 184. Agora tem que tirar 10, porque o objetivo é tirar três. Então já tirei três, foi para 184. Tira 10, ele vai para 174. Essa é a resposta. Perfeito. Mas então você percebe que nesse caso aqui não não é muito bom você falar assim, ó, do 13 até o 187, quanto que falta? É muito mais difícil, né? É muito menos intuitivo você fazer isso, né? Você falar, pô, do 13 até o 187, né? Então você vai,
quando é uma disparidade muito grande, você pega o maior número e tira dele o número pequeno, tá? É a mesma coisa que eu falar assim, ó, quanto é 240 243 - 1? Você vai falar 243 - 1 é 242. Você não vai falar assim, ó, do um até o 243, quanto eu preciso? Não faz sentido, tá? Agora, quando você pensa, olha só, olha o que que você pensa agora. E se for 384 - 347? Eles estão eles estão grandes e estão bem próximos. Olha como é que agora seria difícil você fazer 384 - 300. Então
vamos lá. - 300 dá para fazer, mas você vai falar 384 - 300 84. 84 - 40 44 - 7 primeiro ele perde 4, depois ele perde trê perde quatro, vai pro 40, perde 3, vai pro 37, tá? Olha a dificuldade. Agora, se tu falar assim, ó, eu estou no 347 e eu quero ir pro 384, é melhor assim, tá? Você fala: "Eu tô no 347 e eu quero chegar até o 384". Assim é o melhor mecanismo nesse tipo de caso aqui, tá? Porque aí você fala assim, ó, tá? Do 347 eu vou até o
350. Aí eu já botei aqui três unidades. Agora do 350 pro 384 dá para ver que faltam 34, porque do 350 até o 380 faltam 30 e depois você bota mais quatro. Então você viu primeiro eu fui do 347 até a fechar a casa mais próxima. Então 3 4 7 fechei 350. Eu já tenho três. Do 350 pro 384 faltam 34. 34 + 3, 37 é a diferença entre eles. Pronto. Tá? Então aqui, ó, é melhor pensar no 347 e subir até o 384, tá bom? Aí eu ainda descrevi o mecanismo aqui na apostela, né?
Se eu estou no 347, o que que eu preciso fazer? Eu somo mais 3 e fecho 350. E agora somo mais 30 e vou para 380. Já tenho 33, né? Porque eu somei três, somei 30. Falta somar quatro, né? Para sair de 384 e ir até o o 384. Então eu já tinha 33. Agora eu tenho 37 porque eu vou ter que somar mais quatro. Beleza? Resumindo, eu percebi que 347 até o 384 eu tenho que adicionar 37 coisas, né? Porque eu botei mais três, depois botei mais 30, depois botei mais quatro. Isso dá o
total 37. Tá bom? com a prática de exercício e com as aulas teóricas mais detalhadas, iremos pegando o jeito nisso. Ou seja, pronto, agora a gente vem pra prática de exercício e tá aqui o exercício três, efetuei as seguintes operações sem utilizar o papel, apenas mentalmente. Então vamos fazer juntos. Aqui na plataforma S, eu te falei, eu sempre vou fazer os exercícios com você todos, tá bom? Tanto esses aqui que são simples, quanto até a gente ir chegando nos mais complexos, beleza? Então vamos junto fazer aqui os exercícios. É só essa apostila aqui tem 250,
então a gente vai ficar com módulo extremamente robusto, tá bom? Vamos nessa, então. Vamos cair para dentro. Vamos lá então. Bora. 34 - 3. É óbvio que eu não vou fazer 3 até 34. 3 até 34. Primeiro eu boto 30, depois eu boto mais um. 31. Não, 34 eu removo 3. Ele vai cair pro 31. A resposta é 31. Então aqui, ó, 31. Eu tenho 47 - 12. Cara, eu vou pensar no 47, eu tiro 12. 47 eu tiro 10, vira 37. Tiro 2, vira 35. Perfeito. 68 - 14. Eu vou pensar no 68 e
vou tirar 14. Então 68, posso tirar primeiro 10, depois o 4 ou primeiro 4, depois o 10, tá bom? Então 68, ele cai 10, vai pro 58, cai mais 4, vai pro 54, tá? 543 - 53. Ainda assim, eu acho melhor pensar no 243 e tirar dele o 53, tá? Então 243, vou remover 53. Mas cara, e se primeiro eu remover 43? Então ao invés de eu tirar o 53, eu tiro 43. Aqui vai ficar o quê? 243 - 43, 200. Só que ainda falta 10 para tirar. 190 é a resposta, tá? Você viu? Eu
peguei o 53 e eu tirei o quê? - 40 e depois menos eh perdão, tirei -43 e depois tirei -10. Tirei aqui -53. Mas por que que eu tirei primeiro -3? Porque eu vi que tinha 243. Então já tirei ali 43 para ficar 200. Agora eu tiro 10, fica 190. Bem fácil, tá bom? Então 987 - 47, mesma coisa. Eu vou pensar no 987 e vou tirar 47. Então 987, vou tirar o 7 primeiro. 980. Agora 980 men o 40, 940. 980 - 40. Eu sei que 80 - 40 é 40. 940. Você viu? Eu
acabo preservando, né? Eu tenho que preservar o tempo todo a casa da centena. Só para detalhar para você o que que eu fiz. Fiz 987 - 47. Eu tirei o quê? -7 e - 40, tá? 987 - 7 eu vi que dava o quê? 980. Agora eu tenho 980 - 40. Eu tenho que ter a estabilidade de saber. Cara, eu não tô mexendo na casa da centena, o 9 tá ali. É o 80 menos o 40, vai continuar sendo 900, mas agora 940. Beleza? Então você vê como que o conhecimento sobre as ordens, as classes,
sobre a decomposição dos números, como que tá tudo perfeito, né? Como que tá tudo bem encaixado, né? Como que tudo realmente faz a diferença, tá? Como que tudo é necessário. Beleza? Show. Então vamos nessa. Bora lá. 1065 - 56. Da mesma forma, eu vou fazer o 1065 - 56. Então, primeiro, cara, eu posso tirar aqui o seis, que já eu já acho que o se o seis é o mais chato de tirar. Então, já vou tirar logo. Eu tenho aqui o 165. Quando eu tiro o seis, eu tenho que ter o seguinte, eu vou tirar
o seis, mas primeiro eu vou tirar um 5, vai ficar 1060, e eu vou tirar um, vai ficar 1059. Concorda comigo, né? É isso. 1065 - 6 dá 1059. Agora que eu tenho 1059, eu tenho que tirar o 50, porque eu só tirei o seis. Então fica o quê? 1009. 1009. Tá? Então você vai acostumando seu cérebro com isso, você vai ver que fica automático e na hora da prova você vira uma máquina, você poupa muito tempo. Tá bom? Vamos mais. 1230. E eu elaboro os exercícios para trabalhar justamente cada habilidade que você tem que
ter, tá bom? Então vamos lá. 1230 - 730. Então vamos lá. 1230. Eu vou tirar primeiro esse 30, vai ficar 1200. Agora 1200 - 700. Eu tenho isso aqui, ó. 1200 - 700. Eu só tô fazendo no papel para te mostrar, tá bom? É para fazer de cabeça. Mas 1200 - 700 eu vou enxergar. Eu tenho 1200, eu vou tirar 700. Eu consigo, cara. Primeiro dá para ver que tem 500 de diferença entre eles, mas se você quiser, você faz essa etapa assim, ó, do 700 até o 1200, quanto que falta? Então chega aqui, ó.
1230 - 730. Tirei o 30, agora é 1200 só. - 700. Do 700 até o 1200 é o quê? 700 até 1000, falta 300 e mais 200 500. Tá bom? Então a resposta aqui é 500. Agora 1200 - 700 você tiraria primeiro 200 dele. Tira 200 fica 1000. Agora tira 500, né? Porque você só tirou 200. Agora você tem que tirar também o 500 para você ter tirado 700. Então tirou 200 fica 1000. Tira 500 fica 500. Tá? 765 - 16. Primeiro eu vou tirar o 6. Então 765 - 6 eu tiro 5 fica 760.
Tiro 1, fica 759. menos o 10 que falta fica 749. Beleza? 49 - 38. Aqui eu já vou do 38 até o 49. Do nada eu percebo, Do nada eu percebo que fica melhor assim. Do nada eu percebo que fica melhor assim. Tá bom? Então aqui, ó, do 38 para eu ir até o 49, como é que faz? Do 38 pro 49 eu vou botar e 10, vou pro 48 e vou botar mais um ainda. Então é 11 que falta, tá? do 38 para chegar no 49. Eu tenho 38, 48 e mais unzinho, tá? 133
- 63. Vou tirar logo o três. Então 133 - 63 é a mesma coisa que 130 - 60. 130 - 60, vamos tirar. Eu tenho 130, vou tirar o 60. Vou tirar logo 30, depois tiro mais 30. 130 - 60 eu tiro 30, fica 100. Tiro mais 30, fica 70. Removi o 60 em duas partes. Primeiro tirei 30 para para fazer o 130 virar o 100. Tirei mais 30, virou 70. 999 - 33. Tá bom? Você já pode ver que você vai tirar três da unidade, três da dezena e três da centena, vai virar tudo
seis, tá bom? Vai virar 66 me6 me6. Agora, se você pegar 999 - 333, pegar 999 - 300 dá 699. - 30 dá 669, - 3 dá 666. Tá bom? Mas aqui o melhor jeito, é claro que essa conta aqui, o melhor jeito mesmo é você perceber que você tem aqui a diferença de seis coisas na unidade, seis coisas na dezena e seis coisas na centena, tá bom? Então, meia meia meia. Beleza? Agora 1765 - 415. Beleza? Vamos lá. Eu vou estabilizar o 1765 e vou remover o 415. Então eu tenho aqui 1765 - 415.
Tá? Como é que eu faço isso aqui? Então vamos lá. Eu vou tirar logo o 15 daqui. Vai ficar 1750 porque eu tirei, eu tirei um 15, tá? Então 65. Quando eu vejo 65 - 15, eu tenho que saber que isso dá 50, porque 65 - 5 60 - 10 50. Então aqui, ó, 1765 menos o 15 dá 1750. Agora que eu tenho 1750, falta eu tirar o 400. Como é que eu vou tirar o 400 daqui? Eu tenho que visualizar que isso vai voltar pro 1350. Pedro, como assim 13? Cara, tu tem que ter
em mente que o 7 menos o 4 dá 3, entendeu? Então, se tu tem aqui, ó, 750 - 400, é só o 700 que importa. 700 - 400 dá 300, entendeu? Então, 750 - 400 dá 300 também. Só que esse 50 aqui ninguém mexe nele, então dá 1350, tá bom? Porque você só subtrai o quê? quatro centenas aqui de sete centenas dá três centenas. Beleza? Então, pronto. Opa, tô aqui de novo. Então, parabéns. Concluiu a adição e subtração. Agora a gente vai entrar em multiplicação. E como eu disse, né, aqui eu já vou partir direto
pros cálculos de multiplicação, tá bom? Então, é mais para te dar uma demonstração pra gente passar por isso. Tem o curso de cálculo mental gratuito aqui no YouTube também, mas fica nesse aqui que você vai gostar bastante. Mas caso você não consiga acompanhar, fica tranquilo, daqui a pouco você vai pegar o jeito. Mas pode ser porque você tem deficiência em tabuada. Se tu tem deficiência em tabuada, tem que aprender tabuada, né? Não precisa parar agora para aprender, mas é bom aprender, é necessário aprender, é obrigatório aprender. E eu vou fazer um vídeo em breve também
explicando a tabuada aqui como é que você decora. Se ele já tiver disponível, você procura ele, pausa essa aula, procura. Se não tiver, você segue nessa aula aqui. Mas tabuada é um requisito, tá bom? E eu não expliquei nessa aula aqui porque tabuada é é ainda um nível muito mais baixo, mas eu vou fazer outra aula explicando tabuada, caso você queira, tá bom? Não deixa de curtir e tá aí comigo engajado no vídeo. Vamos nessa agora. Pode seguir que você vai conseguir acompanhar sim, provavelmente. Vai nessa e depois você me conta. efetue as seguintes multiplicações.
Eu vou eu vou descrever aqui os mecanismos de multiplicação que você tem que utilizar, tá bom? Então, vou descrever aqui esses mecanismos. Quero que vocês se concentrem, mas que entendam que isso aqui tem que ser feito sozinho de cabeça. Então, depois você tem que fazer tudo isso aqui de novo sozinho e verificar se você é capaz. Tá bom? Vamos lá. 7 x 14. Eu faço primeiro 7 x 10 e depois 7 x 4 eu quebro o número. Então 7 x 10 eu sei que vai dar 70. 7 x 4 vai dar 28. Quando eu junto
70 com 28, eu visualizo que isso vai dar 98, tá? Essa é a resposta. Então, 98. Beleza? Eh, simples, básico, né? Tem que saber fazer. 8 x 24. Quanto é 8 x 20? 8 x 20 é o 160, né? Então você vai começar a perceber que eu fiz 8 x 20 e eu fiz dessa forma aqui, né? 8 vezes o quê? 20 + 4, tá? Então, primeiro 8 x 20, depois 8 x 4. Isso é a aplicação da propriedade distributiva a nível mental, tá? Eu posso fazer isso. E aí 8 x 20 eu sei que
dá 160 porque 8 x 2 dá 16. Então não é 2, né? São são 20 dá 160 e 8 x 4 dá 32. Então 8 x 20 160. 8 x 4 32. A resposta aqui então é 192. Beleza? Isso é uma coisa mais segura e mais é sólida do que você fazer no papel. Inclusive, né? Você na hora da prova você vai perceber que não existe dúvida nisso aqui. Quando você pega prático, isso aqui não é uma coisa, sabe? Tem gente que pensa: "Isso aí é arriscado, né? Tá fazendo de cabeça". Não, isso aqui é
cálculo simples mesmo. 3 x 72. Não dá para ter dúvida que isso aqui é você visualiza que é 216 instantaneamente, né? Porque 3 x 70 é 210. Já que 3 x 7 é 21. 3 x 70 é 210 e 3 x 2 é 6. Então 216. 2 x 232. Você percebe que eu prefiro fazer o menor vezes o maior, né? E não o 232 vezes o número 2. Então dobrar o 232, né? Eu dobro 200, dá 400. E eu dobro 32, dá 64. Ou eu dobro 30, dá 60. Dobro 2, dá 4. Então 2 x
200, 400. Com 64, 464. 2 x 83 eu vou dobrar o 800, isso dá 1600. Já que 2 x 8 dá 16. 2 x 800 dá 1600. Guarda esse 1600 na sua mente, tá? Evita escrever. É para você desenvolver sua mente aqui. E 2 x 60, né? 2 x 63. O 2 x 60 dá 120. Então eu já tinha 16 + 120 eu já pulei para 1720. Com 2 x 3 que dá 6 dá 1726. 2 x 341. 2 x 300 e 2 x 41. É claro que é 82, porque 2 x 40 é 80.
2 x 1 é 2. Então 2 x 3 4 1 dá justamente 600 + o dobro de 41 que é 82. 682 e 4 x 98. aqui começa, a gente começa a ter que utilizar, a gente vai ter mais produtividade aqui, começando a implantar alguma das técnicas ali de cálculo mental. A gente tá usando muito por enquanto aqui a técnica da decomposição, né? A gente tá sempre vendo o número multiplicando primeiro eh a estrutura maior, depois a menor. Não sei se vocês perceberam. Quando eu falei 2 x 341, eu multipliquei primeiro as centenas, duas xes
300. Depois eu multipliquei as dezenas, 40 e depois 1. Se você já tá mais rápido, você já duplica o 41. A invés de duplicar o 41. 863. Primeiro 800, depois o 60, depois o 3. Agora 4 x 98. É importante você pensar que é mais vantajoso fazer 4 x 100 e depois você corrigir o arredondamento, tá? Então, como é que eu faço 4 x e 98? Eu faço 4 x 100, que dá 400. Mas é importante você perceber que você subiu duas unidades, então o arredondamento é dois, só que você não vai tirar dois, tá?
Porque depois que você subiu duas unidades falsas aqui, depois que você colocou o 98, transformou ele em 100, você subiu duas unidades, você quadruplicou essas duas unidades. Então você tem que descontar oito unidades, tá? Então 4 x 98 você vai ver visualizar assim, ó. 4 x 100 - 892. 8 x 125. Tá? Aqui é muito importante que você visualize que multiplicar qualquer número por oito é dobrar, dobrar e dobrar. Porque o oito ele é isso. Da mesma forma que multiplicar alguém por quatro e duplicar e duplicar, o oito nada mais é do que isso. O
número oito, ele é exatamente 2 x 2 x 2. Então invés de eu multiplicar 8 por 125, eu faço 2 x 2 x 2. Tá? Então por exemplo, 2 x 125 dá 250. Agora dobra de novo, dá 500. Agora dobra de novo, dá 1000, tá? Então isso aqui é um resultado que você vai ficar bem familiarizado, que 8 x 125 dá 1000, tá? Eh, 4 x 72, eu vou dobrar e dobrar porque o 4 é isso, o 4 é 2 x 2. Então eu faço 2 x 72 primeiro, que dá 144, tá? Por que que
eu sei que dá 144, né? Porque 2 x 70 dá 140, né? 2 x 7 dá 14, 2 x 70 dá 140, né? Mas não é 2 x 70, né? Que é dá 140. 2 x 72. Ainda tem ali um dois que vai virar um quatro. Então 144. Agora eu dobro de novo esse 144. Quando eu fizer 2 x 144, né? 2 x 140 dá 280. 2 x 4 dá 8. Então 288 é a resposta, tá bom? Então, ou seja, eu peguei o 72, eu visualizei ele como sendo 144 e agora ele foi duplicado para
288, né? O dobro de 140 aqui dá 280, até porque o dobro de 14 dá 28, né? Então você tem que começar a ter familiaridade com isso. É realmente o dobro de 14 dá 28, né? 14 x 14 + 14, né? Tem ali um 10 e um 10 formando 20, um 4 formando 8. Então o dobro de 140 dá 280, mas esse 4 aqui também dá 8. Então 288 é a resposta, tá bom? Eh agora aqui, quanto é 3 x 12 x 7? Você tem que definir uma ordem para você fazer isso, tá? Vamos supor
que você faça na ordem normal. Você tá aqui, tanto faz, né? A ordem que você executa aqui o produto, o o a multiplicação dos fatores não vai alterar o resultado desse produto. Você pode fazer 3 x 12, pegar o resultado de fazer vezes 7, pode fazer 3 x 7, depois multiplicar o resultado por 12. Tanto faz, cara. Vou fazer na ordem que tá aqui mesmo. Então quanto é 3 x 12? 36. Eu só tô escrevendo para mostrar para vocês, tá bom? Agora eu tenho que fazer 36 x 7. Você agora vai fazer 7 x 36.
Você vai ver que não é difícil, tá? Porque 7 x 30 é 210. Da mesma forma que 7 x 3 seria 21. 7 x 30 210 e 7 x 6 a gente sabe pela tabada que é 42. Então 210 + 42 vai dar 252. Concorda comigo? Como tá isso para vocês? 252. Vou ligar aqui o chat rapidinho. Me falem aí como é que tá. Tá tá dando para acompanhar? Legal. Podem mandar aqui para mim, tá? 8 x 99. Tá bom. Tá tranquilo. Legal. Tá entendendo? Ótimo. Ótimo. Todo mundo tá entendendo, pelo visto, né? Beleza. Tem
aqui o quê? 520 pessoas ao vivo. Legal. Então, olha só, eh, concentra aqui agora. Vamos, vamos começar então a ganhar um pouquinho mais de ritmo, tá bom? Vamos lá. Vamos lá. Eh, tão pedindo para deixar um tempinho para resolver, mas, galera, eh, resolve antes da aula, tá? É melhor assim. E aí eu quero também já deixar claro o seguinte, que eu vou colocar lá no módulo de nivelamento aulas de reforço disso aqui, porque que eh eu vou juntar mais aulas lá, né? Hoje mesmo vou colocar já as aulas que já estão na alfabetização matemática, que
tem aulas lá que eu fico horas a fio fazendo isso aqui. Vai ser bom para quem tá com dificuldade, tá? Então, eh, 8 x 99, a gente vai fazer o quê? A gente vai fazer o mesmo macete do arredondamento. Por exemplo, aqui, será que vale a pena fazer duas vezes e transformar o 8 em 2 x 2 x 2 e fazer 2 x 99 x 2? Não, aqui é melhor eu fazer assim, ó, 8 x 100, que daria 800. Só que eu aumentei em uma unidade, não foi isso. Aumentei em uma. Só que esse um
que eu aumentei, eu tenho que tirar no resultado. Mas pera aí, esse um que eu aumentei, ele foi multiplicado por 8 ainda. Então 8 x 99 é 8 x 100, que dá 800. Só que como eu aumentei uma unidade e essa unidade foi o duplicada, eu vou ter que descontar 8. Então 800 - 8, na verdade a resposta é 792, tá? 8 x 99 é 8 x 100 - 8 porque esse 1 foi o que duplicado, tá? 3 x 132, ao invés de 132 x 3, né? Eh, 3 x 100, 300, 3 x 30, 90,
tem 390. E 3 x 2= 6, 396. Você vai multiplicando sempre da centena para dezena para unidade. Acabou. Tá bom? Eh, uma menina falou ali, ó, nossa, eu sou péssimo em tabuada. Então, é disso que eu tô falando. Tem aulas lá no alfabetização matemática que eu vou botar junto aí no ciclo, que eu explico a tabuada ali toda. E vocês precisam disso. Quem não sabe tabuada, primeira coisa, é bizarro. Você não tem como, é impossível que você se desenvolva matemática sem saber a tabuada. Então isso é a mesma coisa que você, não sei, não existe
explicação, é impossível, só que ao mesmo tempo é muito fácil de aprender a tabuada. Você só não aprendeu porque falharam na tua educação, não tem problema, mas agora é tua responsabilidade de aprender. Eu vou, tô aqui para ajudar, tá bom? Então vamos lá. 3 x 133. Cara, eu quero que você perceba que a resposta tem que ser o quê? Três unidades a mais que a de cima, né? Eu nem vou olhar. Tem que ser. Por quê? Porque a de cima era três vezes o 132, agora é 3 vezes o 133. Então ele é uma unidade
maior. O 133 ele é um ele é um negocinho maior do que o 132, mas esse um negocinho tá triplicado, né? Então de 396 vai dar 399. Você você visualizou isso? É só eu botei uma uma depois da outra aqui só para ver se vocês perceberam isso, né? Se você falaria assim: "Ah, nem preciso executar aqui porque uma unidade maior vezes 3 vai dar três unidades maiores no resultado, tá? Agora 3 x 100, 3 x 30 90, 390, 3 x 3 9 399, tá? 3 x 143, tá? 3 x 100 300 x 40 120 já
que 3 x 4 daria 12 3 x 40 120 então tem 300 + 120 4209 porque 3 x 3 dá 9 tá tá tranquilo, né? Então assim 3 x 100 3 x 40 120 420 já junta vai aglomerando o resultado enquanto você faz a conta vai juntando o resultado na sua mente, tá bom? Não deixa para juntar tudo no final, você vai juntando enquanto você faz. 9 x 9 x 9. A tabuada me diz o quê? Que 9 x 9 é 81. Agora eu preciso fazer 81 x 9, tá? Como que você visualiza isso? Você
faz 9 x 81, tá? Aí você vai fazer o 9 x 80, depois o 9 x 1, que vai dar 9, tá? 9 x 80 é 720. Já que 9 x 8 é 72, 9 x 80 720, tá? E aí o 9 x 1 é, lembra? Era 9 x 81. 9 x 80, 720 + 9 x 1 9 729. Tá? Eu tenho certeza que nessa aqui tem muito mais chance de alguém aqui agora ter travado porque não sabe táó. Se você travou nessa aqui é porque você não sabe a tabuada do nove direito, entendeu? Você
tem que entender o seguinte, saber a tabuada não é saber a tabuada não significa: "Ah, Pedro, se eu pegar para escrever a tabuada eu consigo escrever". Não. Saber a tabuada é assim, ó. Qualquer número que eu te perguntar, você vai saber na hora. 9 x 6 54 em até 1 segundo. 1 segundo. Se você não consegue responder em 1 segundo, um. Eu tô dizendo literalmente um. Um é isso aqui, ó. 9 x 8 72. Se você não tem um tempo de resposta de tabuada de 1 segundo, no máximo 1 segundo e meio, você não sabe
a tabuada. A tabuada não pode ser algo que você pensa. A tabuada, ela tem que ser uma coisa totalmente automatizada, tá? Muito cuidado com essas ideias de que, ah, não, eu vou deduzindo a tabuada. Eu já vi muito aluno ter deficiência matemática severa. Por quê? Você fala assim para ele 7 x 5, aí ele 7 14 21 28 35. E você sabe a tabuada? Claro que não, de forma alguma. Ele não sabe a tabada. 7 x 5 é 35 em meio segundo. 7 x 6 42. 7 x 7 49. 7 x 8 56. 7 x
9 63. Não, não, não existe tempo de resposta para tabuada. Taboada é algo que tem que ser decorado. Ninguém, ninguém pode pensar na tabuada. 8 x 6 48, entendeu? Não pode ter 8 x 8. É, é na hora. Eu tô sendo bem enfático com isso mesmo. 8 x 5, 40. Não tem tempo para pensar na tabada. Aí talvez agora alguém algum eu, eu tenho 500 e poucas pessoas assistindo aqui só no vivo, né? Alguém pode pensar assim: "Ah, nossa, que é isso? Como assim?" Cara, você não tá entendendo. Só bicho, em toda a escola minimamente
normal, minimamente séria do Brasil, isso que eu falei agora de você ter a tabuada instantaneamente decorada, isso é exigido das crianças de 7 anos. Todas as criancinhas de 7 anos tm a tabuada decorada. Na minha escola mesmo, que eu estudei quando era pequeno, não era uma escola cara, era uma escola normal, decente. Eu tinha 7 anos, era o quê? Ia lá na frente, você ia lá na frente da escola da sala, a professora começava a te perguntar, tá boda? Tá, tá, tá. E você tinha que falar tudo na hora. Se você não tem essa habilidade,
é porque falharam na sua educação. Só tô querendo te alertar de que isso não é uma coisa normal. E aí isso justifica muita coisa que às vezes você tem dificuldade, você não sabe por quê. Então vamos resolver com esse foco, tá bom? Tô só te convidando pra gente resolver esse problema aí com muita seriedade. Não, você não pode prosseguir sem ter um domínio eh imbatível da tabuada, um domínio perfeito. Isso é uma coisa muito básica e eu quero muito que você tenha isso, que você entenda isso que eu tô te falando agora. Falar assim: "Cara,
realmente é inaceitável não saber a tabuada. Uma criança tem que saber a tabuada. Como é que eu não vou saber a tabuada?" E saber rápido, tá? Acho que ficou bem claro, porque senão a gente vai passar o ano inteiro junto e você vai est sempre com problema em matemática, sempre, porque toda hora eh não sabe que 7 x 8 é 56, tem que pensar. Isso vai travar o teu exercício, tu vai perder o raciocínio das questões, tá? Como é que você decora a tabuada? Repetição extrema. Repetição extrema e muitas vezes, tá? Por que que muita
gente hoje em dia não sabe tabuada? Por causa da mentalidade de, ah, não, decorar é uma coisa ruim. Então, se você acha que decorar é uma coisa ruim, você vai ser trucidado pelos que decoram, porque os que decoram são muito mais fortes. Quem decora é muito mais competitivo do que você. Decorar é muito importante. Isso é uma coisa de preguiçoso, de, ah, não, eu não decoro, eu Isso aí se aplica em outros cantos, em outros raciocínios, se aplica agora tabuada é para ser decorada, tá? Então, vamos lá. 8 x 16, cara, eu vou pegar o,
eu vou visualizar o 8 como sendo 2 x 2 x 2. Então vou duplicar, duplicar e duplicar o 16, tá bom? Então, 16, dupliquei, virou 32. Dupliquei, virou 64. Dupliquei, virou 128. Beleza? Então aqui, ó, dupliquei o 16, ele vira um 32, né? Porque eu tenho 16 + 16. Então eu vou fechar ali o 15. 15 já geraria um 30. Sobrou um ainda, gera um 32. Agora duplico o 32. Duplicou o 30, vira 60. E o 2 vira 4. 64. Duplicou o 64. Duplicar o 60 gera 120. Duplicou o 4, gera 8. 128. Beleza. 6
x 999. Aqui tá implorando, né? Você vai visualizar na hora. 6000 - 6. Concorda? Porque você vai subir uma unidade para arredondar isso aqui para 1000. Só que essa unidade ela vai ser se duplicada, então você vai remover seis. Então 6 x 999 você vai ver 6000 - 6 vai dar o quê? 5000 994, tá? Tem muita gente que tem dificuldade ainda com esse tipo de subtração, tá? Você tem 6.000 inteiro, você vai remover seis, né? Então você tem que manter ali o quê? Você tem 6.000, você tirou seis, pô, esses seis caem ali do
final, entendeu? É, tem 5990 e4, só saiu seis ali, tá? 9 x 399. Tá? Várias formas de fazer isso aqui, mas a melhor o quê? 9 x 400 - 9. Beleza? É instantâneo. 9 x 400 a gente sabe que dá 3600, né? Porque 9 x 4 dá 36. Então 9 x 4 dá 36. 9 x 400 dá 3600. Só que essa uma unidade que eu arredondei para virar 400, ela foi multiplicada por 9. Então é 3600 - 9 que dá o quê? 3.000. Tinha 3600, então vai ficar 3.500 e quanto? E 90 é 1. Você
tirou nove. Se tu botar nove aqui de volta, ele volta a ser o 3600. Você tá entendendo? Matemática é prática. Matemática é a gente ficar praticando, se expondo aos números, tá? 13 x 3 x 10. Cara, eu vou fazer logo 3 x 13, que dá 39, né? Porque 3 x 10 dá 30. 3 x 3 dá 9. Então 39. E 39 x 10, eu só tenho que adicionar mais um zero, né? Então tenho 39 x 10, 390. 57 x 20. Galera, o macete aqui para multiplicar por 20 é você visualizar o 20 como quê? O
20, na verdade, é um 2 x 10. Então eu vou duplicar e depois vou multiplicar por 10. 2 x 57, 2 x 50, 100. E 2 x 7. 114. 114 x 10, 1140. Beleza? Então vamos lá. 2 x 57, 2 x 50 dá 100 e 2 x 7 dá 14. 114. Multiplicou pelo 10, né? Porque o 20 foi dividido em 2 e 10, tá? Já fiz o dois, agora faz 10, dá isso aqui, tá bom? Então essa aí é é a é a resposta. Beleza? Pronto. Tá? O próximo aqui a gente faz eh as divisões.
Eu vou fazer logo nessa mesma aula para deixar tudo compactado, tá bom? Então aqui, ó, efetue as seguintes divisões mentalmente sem o auxílio do papel. A divisão ela depende igualmente da tabuada. É a mesma coisa, galera. Não tem aqui o que explicar. Aqui a gente tem que fazer e você tem que se familiarizar, tá bom? Então vamos lá. Quanto é 54 di por 6? Cara, isso é a tabuada. 54/ 6 é 9, entendeu? Se você fizer 6 x 9, você volta pro 54, tá? Então, eh, só um instantinho aqui. Pronto. É isso. 54/ 6. Só
queria dar uma palavrinha sobre isso de você visualizar assim, ó. 54 div por 6, né? Que pergunta é essa? Eu acho que eu só vou falar um pouquinho melhor sobre isso para ficar melhor para vocês, tá bom? Quando eu digo 54 div por 6, eu tô querendo pegar 54 coisas, tá? 54 coisas. E eu quero dividir em seis agrupamentos. Eu quero pegar essas coisas e botar dividir para seis pessoas, tá? Então, quando eu tenho 54 coisas e eu vou dividir para seis pessoas, quantas coisas cada pessoa recebe? Recebe nove, tá? Então isso quer dizer o
quê, né? que 54 dividido para seis pessoas a gente consegue formar seis grupos deve, tá bom? Então seis grupos de 9 dá o quê? 54 de novo, tá bom? Então a pergunta é essa. Quando eu faço 54 di por 6, tô falando assim: "Olha, dentro do 54, quantos pacotes tem, né? Quanta, quantos grupos dá para eu formar, né? Sendo que eu tô querendo formar, na verdade, seis grupos, né? Se eu for pegar o 54, dividir em grupos de seis, quantos quantas coisas entram em cada grupo?" Entram nove coisas em cada grupo. Beleza? Então aqui só
para falar um pouco assim da lógica da operação, tá bom? 34 di por 2, eu vou visualizar que eu tô partindo ele no meio. Então eu tenho 34, eu vou partir no meio, né? Eu vou partir o 30 e depois o 4, beleza? Então isso aqui quando eu divido 34 por 2, é a mesma coisa que eu dividi assim, ó, 30 + 4 entre parêntese por 2, eu vou também aplicar a distributiva, né? Então 30/ 2 dá 15 e 4 * 2 dá 2. Então 15 + 2 dá 17. Essa é a resposta, 17. Tá
bom? Então aqui 17 84/ 4 eu gosto de dividir por 2 e por 2. Eu sempre visualizo o 4 como sendo um 2 x 2. 84 por 2 dá 42, né? Porque metade de 80 é 40, metade de 4 é 2. Então 42. 42 por 2 dá 21. Porque metade de 40, eu tenho 42 por 2, metade de 40 é 20. Metade de 2 é 1. Então a resposta aqui é 21. É claro que 4 x 21 vai voltar a ser 84, tá bom? 150/ 2 dá 75. Isso aqui é quase uma coisa que você
tem que decorar, tá bom? 15 por 2 dá 7,5, né? 1500 por 2 dá 750. Eh, quanto que é 150 di 2? A metade de 100 e metade de 50. Então, divido o 100 e o 50, metade de 100 é 50. Metade de 50, 25, dá 75. 65/ 2. Eu vou dividir o 60, depois o 5. Beleza? 60 por 2 dá 30. E 5 * 2 dá 2,5. 5 * 2 dá 2,5. Então 32,5 é a resposta. 350/ 2. Beleza, vamos dividir o 300 por 2. O 300 já dá 150, né? Tem que visualizar isso,
né? O 30 por 2 dá 15, o 300 dá 150. Tem que dividir entre o 50. Então 300 por 2 dá 150 e 50 por 2 dá 25. Então dá 175. Essa é a resposta, tá bom? 700 por 4, eu vou dividir por 2 e depois por 2, tá bom? 700 por 2 dá 350. E 350 por 2 dá o quê? Acabamos de ver que dá 175, né? Então 350 por 2 eu vou dividir o 300 dá 150 e aquele 50 dá 25. Então fica 175. Pronto. 10000/ 4, vamos dividir por 2 e por 2.
Então por 2 dá 700 e esse 700 por 2 dá 350. Beleza? Então a gente pegou 10000, abriu 700. Agora pega o 700, abre de novo. Se tu vai abrir o 700, você pode imaginar que tá abrindo o 600, depois o 100. Então abre o 600, dá 300. Abre o 100, dá 50. 350 é a resposta. E se for 1400 di por 8? Eu só vou pegar esse resultado aqui e vou dividir por dois mais uma vez, tá bom? Vai dar um 75. Então, como dividir por 8? É dividir por 2 x 2 x 2.
Aqui em cima eu já tinha dividido por 2 x 2. Agora eu divido só por mais um do. Tá bom? Eu também poderia dizer que dividir por 8 é o quê? 10000, ó, dividido por 8 nada mais é do que dividir por 2 x 4. Concorda comigo? Então, eh, eu já sei o resultado da divisão por 4 é 350. Agora falta só dividir o 350 por 2, dá 175. 324/ 3. Cara, eu vou dividir o 300 pelo 3 e depois o 24 pelo 3, tá bom? Então, e o 300 pelo 3 dá 100 e o
24/3 dá 8. Então, a resposta é 108. Tem isso na apostila, né? Mas como que eu verifico se o número é divisível por três? Eu tenho que somar os algarismos dele e ver se essa soma dá um número divisível por três, tá bom? Então, quanto é 3 + 2? 5 + 4 dá 9. Opa, isso aí é divisível por 3, tá? 981/ 3. Deixa primeiro eu ver se isso dá uma divisão exata, né? Então 981 por 3. Vamos lá. 9 + 8 17. Eu complemento um aqui, né? 9 + 8 entra 1, fecha 10, 17.
Com + 1, 18. 18 é divisível por 3, né? Então ótimo. Isso. Isso só significa que esse número inteiro aqui 981 é divisível por 3 também. Beleza? Como que eu faço isso, cara? Eu vou dividir o 900 e depois o o 81, por exemplo. 900 por 3 já vai dar 300 e 81 por 3 dá 27. Tá bom? Então dá 327. Pedro, mas como que eu saberia tão rápido assim que o 81 por 3 dá dá 27? É uma coisa que você vai decorar com o tempo, tá? Mas você também poderia pensar o seguinte. Então,
eh, Pedro, 981/ por 3. Vamos lá. Você poderia dividir assim, ó, só vou escrever para ficar claro. Você poderia dividir o 900, depois você dividiria o 60 e depois o 21, porque o 60 você vai saber que o 60 por 3 dá 20 e o 21 por 3 dá 7. Concorda comigo? Então aqui, ó, o 300 por o 900 por 3 dá 300, o 60 dá 20, né? 60 por 3 20 20. Então 20, 320 e isso aqui dá 7, né? Então 327 do mesmo jeito. Beleza? 126/ 6. Cara, eu quero que você visualize que
eh tem aqui dentro um 120, né? Então eu vou fazer 120 por 6, depois 6 por 6. 120 por 6 é fácil, dá 20, né? Porque ó, só para deixar bem claro, eu tô visualizando assim, ó. 120 + 6 di por 6. Tem que dividir é os dois por 6. Então 120 por 6 eu já sei que dá 20, né? Porque 12 por 6 daria 2. Então 120 dá 20. E aqui dá 1. 6 por 6 dá 1. Então a resposta aqui é 21. 6 x 21 dá 126. Tá bom? 6 x 21 6 x
20, 120. 6 x 1 6 126 é a resposta. Beleza? Mas é 126 por 6 é 21 nesse caso. Tá bom? Então é isso, finalizamos aqui a aula de multiplicação e de divisão, fizemos aqui um pouco de treinamento, agora a gente vai pra próxima. Valeu. Pronto, agora vamos começar a aprender números decimais, números positivos, negativos e operações com números decimais. Você sempre teve dificuldade de vez em 1,2, 0,7, esses números aí são os decimais. Você vai aprender agora, tá bom? Então vamos nessa, cai dentro que você tá indo muito bem. Não desiste não que vai
dar certo. Primeira coisa, um número decimal é o seguinte. Quando você pensa aqui, lembra quando você pensa no um,? Você lembra que você tinha que juntar eh 10 dele para você fazer uma dezena? Aí você lembra que se você multiplicar isso aqui por 10, você junta 100 e assim vai, né? Aí você pode juntar 1000 e tal. Beleza? Eh, o que que é um número decimal? É um número quebrado. É um número quando você tá querendo expressar uma coisa que ela não é nem uma coisa, não é nem um inteiro. Ela é uma coisa quebrada.
Então, por exemplo, se eu botar aqui, ó, se eu pegar esse um aqui, eu consigo dividir ele em 0,5 e 0,5, tá bom? E esses números aqui, ó, se você somar 0,5 + 0,5, você tem o um de volta, tá bom? Então o 0,5 ele significa meio, tá? 0,5 é isso é meio, tá? E aí da mesma forma que quando você junta 5 + 5 você tem o 10. Quando você junta 0,5 + 0,5 você tem 1. É isso, tá? Número decimal funciona dessa forma. Você tem que ter a noção de que isso aqui é
menor do que o número um. Isso aqui é apenas metade do um. Tá bom? Quando você tiver assim, ó, 0,05 + 0,05, isso aqui é ainda menor, tá bom? Na verdade, quando você juntar o eh 0,05 com 0, vê se você entende, né? Esse aqui era zero, só que aí nessa eh nessa primeira casa aqui decimal que aparece, ele já tinha um cinco, né? Legal. Esse aqui é zero e na primeira casa ele também é zero. Então quer dizer, na primeira casa ele não tem nem mesmo um, né? Vamos supor, eu vou só te mostrar
um negócio aqui, ó. Se eu pegar aqui o o 0,5, eu consigo dividir ele em cinco partes de quanto? 0,1 0,1 0,1 0,1 e 0,1. Tá, tá aparecendo para vocês na tela do iPad, né? Claro que tá, né? Falaram ali que não tá. Tá sim. Arrasta aí pro lado para você achar. Tá bom. Então a gente tem aqui vários 0,1, né? Quando você junta todos eles, você tem o 0,5. Cara, só para você entender, o 0,1 aqui é a mesma coisa do que o 0,10, tá bom? É a mesma coisa. Os zeros que eu colocar
aqui agora, eles não têm valor, tá? Os zeros que eu for colocando aqui pra direita não tem valor. Eu sei que normalmente teria, né? Quando eu tenho aqui o 10, eu boto mais um zero, agora eu tenho 100. Eu boto mais um, agora eu tenho 1000, claro, mas não na casa decimal. A casa decimal, ela é a parte quebrada do número. Então eu dizia: "Olha, eu tenho 0,5 coisas" ou dizer: "Olha, eu tenho 0,50 coisas". Ou dizer, "Eu tenho 0,5.000". É óbvio, não se fala desse jeito, mas é tudo a mesma coisa, tá bom? É
tudo a mesma coisa, não muda nada, tá bom? Não produz mais valor pro número, beleza? Então, Pedro, por que que eu colocaria isso aqui? É para especificar os detalhes do número. Por exemplo, não é a mesma coisa, né? Vamos supor que eu tenho aqui 0,5. Mas e se eu quisesse dizer que eu tenho, ao invés de 0,5, eu tenho um pouquinho a mais. Um pouquinho a mais, mas cara, muito pouco a mais mesmo, né? Então eu diria, eu tenho 0,5. Aí eu tenho aqui, ó. Cara, o valor disso é ridículo. O valor disso é irrisório.
O valor disso é muito, muito, muito, muito pouco, tá? Mas muito, muito pouco mesmo, né? Isso aqui é tá lá no final, é uma coisinha, entendeu? é uma fração muito pequenininha do número, tá bom? Se eu colocasse aqui já seria maior. Se eu colocasse aqui já seria bem maior. Se eu colocasse aqui já seria muito maior, muito maior mesmo, entendeu? Então, por exemplo, só para eu fazer um teste aqui com vocês, qual número é maior, né? 0,3 ou 0 V esse aqui? Qual que é maior? Esse ou esse? O primeiro ou o segundo? O maior
é esse aqui, né? Esse aqui é maior, ele tá mais especificado ali no final, né? Lá no finalzinho a gente colocou um, né? Trocinho de nada mais. Tá bom? É óbvio, eles são praticamente a mesma coisa, né? Mas se eu esticar isso aqui, o que eu espero ver é isso aqui, né? Já que ninguém especificou nada, né? A princípio eu espero ver isso aqui, né? Esse aqui ele ainda tem uma especificação lá no final, tá bom? Então ele é um pouquinho maior. Agora vamos lá. Qual número aqui é maior? Qual é maior? O número A
ou número B? Isso é bem importante, tá bom? Qual é o maior? O maior é o segundo. É isso aí mesmo. O maior é o B. O B é maior. Tá bom? Eh, e falar, ele é 10 vezes maior. Não, aí não. Aí você viajou. Para ser 10 vezes maior do que esse número aqui, teria que passar vírgula para frente. Teria que ser o 3,01. Tá bom? Esse aqui é maior porque esse aqui é o 0,301 e esse aqui é o 0,310. Então, é claro que 0,310 é maior do que 0,301. Entendeu? Se eu colocar
agora aqui, ó, 0 [Música] Vã e agora, qual desses três aqui é o maior número? O 0,301. 0,301. Não, o zero no final não conta nada. O zero no final tá aqui só para facilitar tua leitura, tá? Vamos lá. Qual o número aqui é maior? O 0,301, o 0,310 ou o 0,3009? O maior continua sendo o B. O maior continua sendo B. Tá. Mas qual desses dois aqui é maior? O A ou C? Qual dos dois é menor? É maior? O maior é o A ou maior é o C? Pode falar aí, tá todo mundo
respondendo aqui. Eu tô vendo. O maior é o A. O maior é o A. Tá. Valeu, irmão. Tamos juntos. Tchau. Tchau. Falou. O maior é o A, com certeza, né? Basta você eh não tem valor nenhum você colocar zero aqui no final. Você pode fazer isso à vontade, tá? Agora que a gente fez assim, a gente vai conseguir comparar eles melhor. Olha só, a gente botou eles assim, ó. Compara eles agora aqui, ó. 0,30. E aqui 0,300. Concorda? Esse aqui é o pequeno. Pouca coisa, mas é. Esse aqui é o pequeno. Você sabe o que
que acontece se eu botar mais um numerozinho aqui, né? É porque não é nem um déimo, né? Nem um centésimo, nem um milésimo. É um um uma casinha, um aqui é do, centésimo, eh, milésimo. Aqui seria, né, um décimo de milésimo, né, uma coisinha bem pequena. Se eu colocar mais um negocinho aqui, o que que acontece? Ele vai pular para cá, 301, entendeu? Sacou? Pegou? Se eu colocar mais uma unidadezinha aqui, ele pula para cá e vai virar o 0.301, tá? Então, eh, verifica isso. Quando você, quando você quer saber qual dos números é menor,
você tenta colocar um zero a mais aqui só para você deixar eles do mesmo tamanho. Esse zero não vai fazer diferença nenhuma, entendeu? Você iguala elas. Agora eu vou comparar aqui um em cima do outro. Olha só, não fica claro que esse aqui é o maior? Porque ele já tem eh quanto mais uma casa tá pra esquerda aqui, no caso antes da vírgula, mais avançada ela é. E na verdade, se você for ver, né, isso aí sempre é sempre uma coisa normal, né? Quanto mais uma casa tá pra esquerda, mais ela vale. Então a casa
que mais vale aqui é essa casa aqui, né? E aqui embaixo ele tem zero, aqui ele tem um, né? Então essa casa aqui tem mais valor, né? É mais importante esse um aqui do que esse nove aqui. Esse nove aqui, quer dizer, se juntar 10 aqui, ele vem para cá como um. Entendeu? Isso deu para visualizar? Agora, o que que é uma uma coisa bem simples assim para você saber, cara? Para você fazer soma ou para fazer subtração com números decimais, você arma e coloca a vírgula é em cima da vírgula. sempre a gente vai
ver isso para fazer multiplicação, você executa a multiplicação e no final você conta quantas casas decimais tem na multiplicação e coloca no resultado. E para já tá explicado isso na teoria da plataforma SAD bem detalhado, mas vocês vão entender porque que eu tô falando assim mais rápido. E para você fazer divisão, você iguala as casas. Eu vou mostrar isso nos exercícios agora, mas o que eu realmente gostaria que vocês pegassem agora. Sim, o que eu realmente gostaria é que quando eu tô multiplicando, né, você tá acostumado com isso, ó, vou multiplicar 7 x 5, fica
maior, né? Fica 35. Vou multiplicar aqui 12 x 8, né? Fica quanto? 8 x 10 80 + 8 x 2 16. 96 ficou maior. Mas se você pegar e multiplicar por uma coisa decimal, cara, um número decimal menor do que um, ele, né? Veja bem, eu pego o 12, eu faço vezes 8, eu tô querendo saber oito vezes o número 12. 8 vezes o número 12. Concorda? Mas quando eu faço assim, quero saber aqui quanto é 20 vezes 0,5. Cara, quantas vezes eu desejo ver o número 20? Eu não quero ver o número 20 uma
vez, nem duas, nem três, nem quatro. Eu quero ver o número 20 meia vez. Eu só quero meio o número 20, porque eu tô fazendo o quê? Meio, né? 0,5 x 20. Então, metade de 20 é o quê? É 10. Tá? Deu para você visualizar isso? Se eu fizer assim, ó, quanto é 30 x 0,9? Cara, o 0,9 ele não é nem mesmo número um, tá? O 0,9 ele é menos do que 1. Então se eu fizesse uma vez o número 30, uma vez o número 30 daria o próprio 30, mas o 0,9 tem que
dar menos do que 30, tá? No caso aqui vai dar 27 a resposta, tá? E aí no na próxima semana eu vou ensinar melhor a calcular isso, né, de cabeça, né, que isso aqui na verdade é 90% do 30, tá? Vou ensinar melhor a a visualizar isso, mas eh muitas vezes você fica confuso, né, no h prova aparece assim, ó, meio xes me, né, aí isso dá uma coisa ainda menor, isso dá 0.25, 25, né? Sendo que aqui tu poderia ver como 0.50, né? Agora aqui deu, ou seja, tu tá pedindo metade de uma coisa
que já é metade, metade de meio. Metade de meio é 0.25, beleza? Porque você está multiplicando por um cara que ele não é nem mesmo um, ele é menos do que um. Então você vai visualizar o teu resultado como menos do que um também, tá bom? Sacou? Eh, deixa eu mostrar aqui de novo o de 20. Olha só quanto é 20 x. 0,5 é concorda? Porque tu tem um aqui, você tá 0,5. OK. É metade. Metade de um, né? Que número é esse? 0,5. Meio, tá? Quando você faz x 20, quanto é metade de 20?
Metade de 20 é 10. Acabou. Quanto que é x 40? 40 dá 20. Porque meio é o quê? É, se eu falar assim, ó, quanto é 1 x 40? 1 x 40 é 40. Quanto é 2 x 40? 2 x 40 é 80. E quanto é meia xz o 40? Ué, metade dele é 20. Entendeu? Quanto é 0,1 x 40? 0,1 x 40 é apenas o 4.1 é o quê? É 1/o de um número. É você, o que que é o 0,1? Ele é uma parte de 10, né? Quando você pega um, você, da mesma
forma que um, tu pode dividir em duas de meio, por isso que o meio é meio. Tu pode dividir o um em várias partes de 0,1. Várias partes. Quantas? 10. Consegue dividir em 10 partes. Então, multiplicar alguém por 0,1, você só vai ver 1 déo, né? Tu vai pegar e vai dividir essa pessoa em 10 partes, tá? multiplicar por 0,1 é a mesma coisa que dividir por 10. Exatamente isso. Tá bom? Beleza. Então, eh, é isso, né? É uma expressão de uma porcentagem. Semana que vem eu prometo que a gente vai ver isso com calma,
tá bom? Então, agora eu vou colocar aqui, ó, eh, né? Visualiza aqui agora, né? Eh, execute as seguintes operações mentalmente, sem o auxílio do papel. Então, aqui a gente tem só operações decimais. Eu quero ensinar você a pensar mesmo em operação decimal, tá bom? Vamos lá. Agora, ã, 3 x 0,2. Cara, quanto? Me diz uma coisa, eu vou fazer isso aqui bem devagar, porque eu sei que vocês estão tão estão com um pouco de dúvida nisso, né? Quanto seria 3 x 2? Seria 6. Concorda comigo? E 3 x 0,2 é 0,6. Eu gostaria muito que
você visualizasse, né? 3 x 0,2. Concorda? É o 0,2 mais o 0,2 que já dá o quê? 04. Isso aí. Aí, mais um 0,2 dá o quê? 06. Se tivesse mais um 0,2 quanto? 0,8. Se tivesse mais um 0,2 quanto? Um. Ia dar um inteiro. Se tivesse mais um 0,2 ia dará quanto? 1,2. Entendeu? Tivesse mais um 0,2 era quanto? 1,4. E mais 1? 1,6 + 1 1,8 e + 8 2. Ajudou? Ajudou ou não ajudou? Legal, né? Às vezes é, você nunca tinha visto assim, mas número decimal é a mesma coisa, né? Agora e
se tu tivesse 0,2 e você colocasse + 0,02, né? Resposta 0,22, tá? Você tem aqui, ó, só você completar que você vai saber, você vai tem 0,20 + 0,02, pegou? Dá 0,22. Aí, nesse 0,22, vamos colocar agora mais 0,02. Ó, caramba, eu tô hoje bem didático. Olha só, 0,22 + 0.02, quanto dá? 0,24, né? E 0,24 + 0,2. Quero ver quem acerta. 0,44. Eu tinha 0,24, mas agora eu não botei 0.02 para ir para 0,26. Eu botei 02. Esse 02 aqui é mais um 020 basicamente, né? Então vai pro 0,44, né? Tá entendendo? Exatamente isso
é o conceito de ordem. Eu tô somando aqui numa ordem maior, né? E quando eu boto 0,02, eu tô botando numa ordem menor. Agora, quando eu boto 0,2, eu tô numa ordem superior. Da mesma forma que se eu pegar agora, botar um do aqui, ah, isso aqui mais 2, aí vai direto para 2,44. Aí se eu botar mais 0,02, aí vai para 2 v o quê? 46, entendeu? E se eu pegar agora esse 2,46 e eu somar 0,02, aí daria 2,48, né? Mas se eu somar 0,02, se eu tô botando agora 0,0 em vez de
ter um cara que ele tá aqui, quer dizer, não vai nem conseguir afetar essa ordem aqui ainda. Vai continuar sendo 2,46, mas 2,46 com um detalhezinho do 2 ali no final, 0,462. Esse dois aqui que entrou é pouquíssimo relevante. Aí se agora eu vier aqui somar assim, ó, mais 0,06, quanto é que fica? Fica 2,46 do mesmo jeito, só que nesse doizinho aqui do final vai entrar um seis. Então em vez de ter dois aqui, vai ficar um 8, ó, 0,468, viu? Ficou maior do que 462. E se agora eu vier aqui e somar assim,
ó, 0,002, aí vai dar quanto? 2,468. Mas aí entrou isso aqui. Então 2,400 e Opa, então agora não é mais tinha 468, vou botar um do aqui agora. Vai virar um zero, né? Então posso só dizer que é 2,47. Visualiza isso aqui com calma. Visualiza com calma que você vai ver. + 0.002. Esse 002 completa aqui. Viraria o quê? Faz aqui, ó. Pensa no 68 + 02 não dá 70. Que em vez de botar 70 eu botei 7. Não preciso, não preciso botar é 2,470 ou 2,47 é a mesma coisa, não é? Tá pegando ou
não tá? Fala para mim, confirma aí quem tá no vídeo. Tá pegando. Falou, irmão. Ah, show do portão, né? Valeu. Tá pegando, né? Legal. Isso aqui é só para dar uma aquecida, tá? Só para dar uma aquecida. Vamos fazendo isso aqui, tá? Vamos lá, então. Isso aqui é importantíssimo, tá? Isso aqui é importantíssimo. Eu preciso, eu só tenho que deixar uma coisa aqui bem clara mesmo nessa aula aqui para você ouvir agora. Se você não tá, vamos supor que você teve dificuldade assim, tive dificuldade para entender isso, cara, isso significa aí com certeza um nível
de defasagem enorme, enorme, enorme no teu ensino fundamental. Enorme, absurdo, tá? que nem assim você consegue entender. E aí, que que tem de bom nisso? É você falar: "Ah, tá, então tá tudo bem, porque eu não tô entendendo porque sacanearam minha educação. Então agora eu tô no lugar certo aqui, eu vou aprender, entendeu? Eu tô falando isso para te animar justamente, tá? Você visualizar isso aí na sua cabeça, não, não é culpa minha. Se eu não entendo isso aqui é porque ninguém, isso aqui eu tinha que ter aprendido na minha infância. Agora que eu não
sei, mas eu vou conseguir agora que eu sou adulto. Não tem mistério nenhum. 3 x 0,2 dá 0,6, tá? Eh, 4 x 0,4, entendeu? Aí já teve gente me perguntando assim, Pedro, então é só fazer a multiplicação normal e depois botar dividir por 10. Cara, é, mas eu preferia que você visualizasse mesmo, sabe? Como eu queria que tu visualizasse na tua mente 4 x 0,4. Você realmente visualizar assim, cara, isso aqui é um 0,4. Com outro 0,4 daria 08. Com mais um daria 1,2 e com mais 1 daria 1.6. E aí não é nem que
você precise fazer esse procedimento, mas que você tivesse como enxergar isso. 04 se acumulando e virando 1.6, tá bom? 5 x 0,3. Agora, é claro, você pode também ignorar a existência da vírgula, fazer 5 x 3 e lembrar que isso dá 15, mas que a gente tinha aqui a presença de uma casa decimal. O que é casa decimal? Vou falar para você agora. Casa decimal é casa depois da vírgula, casa válida, tá? Se aqui fosse 0,30, não ia mudar nada, tá? Continuaria sendo normalmente. Se fosse 0,30, ainda assim teria apenas uma casa decimal, beleza? Dá
no mesmo, tá bom? 0,30 é, eu tô falando de casa decimal válida, tá? Se fosse 0,31, teriam duas casas decimais, tá? Calma, eu vou ensinar a usar anotação científica, calma, tá? Então aqui, ó, você faz assim, olha, 5 x 3 dá 15, mas tem uma casa decimal, né? Então você vem daqui para trás, tá bom? Daqui para trás, então uma casa decimal também tem que ter uma casa depois dessa vírgula também, tá bom? 7 x 02. Ah, 7 x 2 daria 14, mas tem uma casa decimal aqui também. Tem que ter uma 1,4. Mas eu
prefiro, né, 7 x 0,2. Você vai ver o 0,2 se empilhando até virar 1.4. Eu só digo assim, você tem que ter essa imaginação. Pelo menos 9 x 03. Se fosse 9 x 3 daria 27, mas com uma casa decimal é 2,7 a resposta. Tá bom? 12 x 01. Cara, quando você for multiplicar alguém por 01, você divide essa pessoa por 10. Ou seja, você só tem que e só pensar, né? Por que que isso funciona? Porque se fosse 1 x 12 não daria 12, mas com uma casa decimal é 1,2. Tá bom? 0,1 é
a mesma coisa que perguntar quanto é 10% de alguma coisa, né? Agora 0,1 x 178 dá 17,8. Concorda? Você só tem que multiplicar por 0,1. Você puxa uma vírgula para trás, né? Vai, é 1 x 178 e puxa uma casa decimal, tá bem? 0,4 + 0,6 1, tá? Isso aí. 0,1 é a mesma coisa que 10% quando você multiplica por alguém, tá bom? Quanto é 0,4 + 06? É 1, concorda? Eh, agora, quanto é 0,4 + 0,06? 0,4 do mesmo jeito, né? 0,4 + 0.0 não muda nada, mas tem um seizinho aqui que entra como
detalhe, fica um pouquinho de nada maior, mas não chega nem a ficar um démo maior, tá? Para ficar um décimo maior, teria que ir pelo menos aqui pro 0,5, né? Não foi, tá? Só para treinar, quanto é 0,4 x 0,6? 4 x 6 não dá 24. Aí eu boto uma casa decimal, né? 2,4. Mas tá errado, tá? Porque são duas casas decimais, tem uma casa aqui e uma casa aqui, tá? Então tem que voltar uma, duas, tá bom? Então a vírgula tem que ficar aqui. Tem duas casas decimais agora. 0,24, tá bom? Você viu que
ficou ainda menor, né? Se eu fizer 0,4 x 0,6, tá ficando ainda menor, né? Porque eu tô querendo apenas 0,4 do 0,6. Eu tô querendo 40% do 0,6 ou tô querendo 60% do 0,4, né? Eu tô pegando um cara que é pequeno e multiplicando por outro também que é menor do que um. Então eu não vou ver ele nem uma única vez, né? Sacou? Peguei um monte de gente aí, né? Um monte de gente. Ah, caí nessa. Quanto é 0,30 + 0,3? É 0,6. Isso aqui é a mesma coisa, né? 0,30. Vocês viram? Eu faço
apostila, né? Eu conheço as manhã. Então aqui é a mesma coisa. É 030 + 030 ou é 03 + 03. Não muda nada esse zero aqui, tá bom? Mas quanto é 0,30? 0, vamos colocar 0 30 x 0,30 é 9, né? 3 x 3 é 9. Só que tem quantas casas decimais? Tem duas, né? Então aqui, ó, uma casa decimal viria para cá, seria 09, mas tem que ser 0,09. Cuidado, tem gente achando que tem quatro casas decimais, pô. Esse 30, esse zero aqui não vale de nada. Isso aqui não tem significado algum. 0,30 é
a mesma coisa que 0,3. Tá bom, beleza. Pô, o moleque ali para mim Pedro, você pode diminuir o volume do seu microfone, cara. Inventaram uma nova tecnologia recentemente que se chama volume do teu próprio computador. Tu pode reduzir ele aí, pôra, mano. Que isso? Tá. Então, vamos lá agora, né? Vamos concentrar aqui mais, tá bom? É 02 + 0 2. Quanto que dá isso aqui? 0 22 visualizou comigo? Todo mundo tá vindo junto, não tá? Tá, tá dando para pegar mesmo. Até quem tem mais dificuldade, eu acredito, né? Valeu, obrigado. Vamos lá, vamos fazer mais.
Vamos lá. 1,45 - 0,15, né? 1,30. Tá? Você visualiza aqui, né? Pô, é simples, né? Eu tenho 1,45 - 0,15. Eu quero tirar o quê? 0,15. De quais ordens, né? Tá entendendo? Eu quero, eu tenho aqui 0 e o 15 aqui é 45 - 15 dá 30. É claro, né? Não é isso? Sacou? Ali perguntaram assim: "Por que que 0,3 x 0,3 não é 0,9?" Ué. Porque 0,3 x 3 é 0,9. Você concorda? Concorda? 0,3 vezes, né? 3 x 0,3 vai dar 036 09, não é isso? Agora eu não pedi 03 três vezes. Eu pedi
o 03 apenas 30% de si próprio, né? Eu não quero nem eu não quero ver ele três vezes. Eu quero ver ele na verdade menos que uma vez. Ele ele não pode ficar 09 porque ele ficou maior ainda. Como assim, né? Se eu pegar o 03 e mostrar três vezes, ele vira o 09. Agora, se eu pegar o 03 e mostrar 0 três vezes, ele vai virar o quê? 0,09. Fica ainda menor, né? Aqui não temos. Aqui o resultado não chegou nem a dar 0,1. Você percebeu? Nem 0,1, né? Que seria a mesma coisa que
0,10. É menos do que 0,1. Menos do que 0,10. Concorda comigo? Quando eu pego aqui o 0,1, galera, eu chamo de 0,10. Eu sei que esse zero não muda nada. É só para facilitar de vocês enxergarem, tá? Porque tem gente que não enxerga fácil. Então eu boto aqui o 10 só para completar e você vê que esse cara aqui de baixo é menor, tá bom? Deu para entender agora? Ô Artur? Sim. Vamos lá galera, todo mundo acordado aí, hein? Vamos lá. 1,45 - 0,15 dá 1,30, tá? E 1,45 men 0,05 quanto que dá? Dá 1,40.
1,40, não é isso? Sacou? Conseguiu ver junto comigo aqui, né? Porque eu tenho aqui, ó, 1,45. Eu tô tirando que é 0,05. Olha, olha a ordem aqui, ó. Tô tirando só daqui. Tô tirando aqui da da da terceira casa que aparece ali, da segunda casa decimal, tô tirando cinco. Então, vou tirar cinco daqui, 1,40. Beleza? Vamos lá. 2,78 - 0,38. Concordo. Eu não vou mexer no 2 aqui. A princípio, eu vou só tirar 38 de 78, né? Vai ficar 2,40 ou 2,4. Não precisa daquele zero ali, tá? Eh, se eu pegar 2,4, somar com 0,3,
quanto que dá? 2,7 ou 2,70? E se eu pegar esse 2,70 e somar com 0,08? Aí volta a ser 2,78, que é o que era antes. Tá bom? Botei 0,38 de volta. Primeiro botei 0,30, depois 0.08. Só para vocês tem que ir criando essa sensibilidade com o número decimal, entendeu? Quanto é 3 di 0? 2. Bem, se fosse 3 dividido para uma pessoa só, vamos lá. Se fosse três dividido para três pessoas, aí três para três pessoas, cada uma recebe só um. Aquele zero no final eu só boto para você visualizar melhor, entendeu? Você não
precisa, tá vendo? Esse 1,30 é a mesma coisa que 1,3. Não tem diferença nenhuma não. Eu só boto para você enxergar, só para você enxergar melhor mesmo, entendeu? Não tem nenhuma diferença. Fosse 3 dividido por 3 ia dar 1. Mas se fosse três dividido só para duas pessoas, elas iam ganhar mais, né? Cada um ia ganhar 1,5, não é isso? Mas se fosse agora três dividido para uma pessoa, ela ia ganhar mais ainda. Ia ficar três só para ela. Agora, e se fosse três dividido para metade de uma pessoa, ela ia ganhar muito mais, porque
eu sei que é é difícil. Isso aqui agora é abstração matemática, tá? 3 dividido para meia pessoa, ela ia ganhar seis coisas. Se eu tenho três coisas e eu vou dar essas três coisas para meia pessoa, a pergunta é quanto que uma pessoa ganha? Eu tenho três coisas divididas para meia pessoa. A pergunta é: quanto que uma pessoa ganha? Tu não dobrou embaixo de meia foi para uma. Então dobra em cima também. Seis. Seis para cada uma pessoa. É porque o resultado da divisão ele é sempre para uma pessoa. A gente faz as divisões com
sempre com resultado um no denominador, entendeu? Então não é que de fato vai aumentar a quantidade de coisas. Tem gente que buga muito com isso, né? Eu tenho aqui, eh, cinco coisas e eu quero dividir, eh, cinco coisas para 0,1 pessoa. Quanto que dá para cada pessoa? Dá 50 coisas para cada uma pessoa. Se tu tá dizendo que tu tem cinco para cada 0.1 pessoa, se tu quando tu tiver 10 vezes mais pessoa, né, em vez invés de ter só 10% de pessoa, tem um, tem 10 vezes mais, vai ter 10 10 vezes mais coisa,
é proporção, tá? Mas enfim, eh, né, você tem outras formas de fazer. Então, por exemplo, quanto é 3 divido por 0,2? Você pode escrever, ó, 3/ 0,2. Agora você pode fazer o seguinte, você pode multiplicar em cima e embaixo por 10. Pedro, por que que eu multiplicaria em cima e embaixo por 10? Você pode fazer isso. Você faz a fração continua sendo a mesma quando você faz isso, né? Por exemplo, eu tenho 1/ 2, isso é metade. Multiplica por dois em cima, fica 2 e por dois embaixo também fica 4. 2 di por 4 continua
sendo metade. Entendeu? Quando você faz uma multiplicação ou uma divisão em cima da fração e embaixo também, você não tá alterando a fração, desde que seja a mesma multiplicação ou a mesma divisão, tá bom? Então, 3 dividido por 0,2 você pode multiplicar por 10 em cima e embaixo. Então, multiplicar por 10 em cima vira 30. E embaixo, multiplicar por 10. Multiplicar por 10 dar uma vírgula pra frente, vira 2. 30/ 2 dá 15. A resposta é 15 mesmo, tá? Então, falaram assim: "Pedro, também dá para tirar uma vírgula do denominador e botar um zero no
numerador". Não, isso não, isso é a mesma coisa que eu tô falando, entendeu? É exatamente isso. É só que isso aí que você tá falando é de um jeito que não é o certo, entendeu? Eu não tô botando um zero, eu tô multiplicando por 10 em cima e embaixo, tá? Esse que eu quero que você saiba. Eu estou multiplicando por 10 cembaixo. Aí perguntaram assim: "Pedro, por que que isso aí não é 1,5, né?" Eh, fizeram uma pergunta ali. Por que que não é 1,5? Ué, que eu saiba, 3 dividido para duas pessoas é 1,5.
Concorda? Não é agora 3 dio para 0.2 pessoas, quanto cada pessoa recebe? Cada pessoa receberia 15 coisas. Aí você fala: "Mas só tem três, Pedro". Eu falou: "Mas é três para 0.2 duas pessoas e a a tua resposta da divisão sempre vem obrigatoriamente para cada uma pessoa. Então acaba sendo uma abstração necessária. Não é de verdade que as três vão virar 15. Aqui, olha, se tu tá dizendo que são três para cada zero, duas pessoas, para uma pessoa vai ser 15. É uma abstração, entendeu? É isso mesmo. O negócio de colocar zero é macete. Você
tem que saber que multiplica em cima e embaixo pelo mesmo valor, entendeu? É isso aí. Esse é o conhecimento da galera. Ai, bota zero. Tá botando zero. Não tá botando zero nada. tá fazendo multiplicação por 10 em cima e embaixo. Aqui multiplicar por 10, você tá, você anda com uma vírgula paraa frente. No caso do 0,2, quando ele é multiplicado por 10, o 0,2 multiplicado por 10, você bota uma vírgula paraa frente, a vírgula fica aqui, a gente chama só de 2. Agora o três, quando é multiplicado por 10, a vírgula já está aqui no
início. Então quando você bota ela pra frente, tem que botar um zero aqui, fica sendo um 30. E essa vírgula aqui também não tem sentido. Pode multiplicar por quem você quiser, em cima e embaixo. Pedro perguntar assim: "Pedro, poderia multiplicar por cinco?" Poderia, né? Então você tem aqui 3 div por 0,2. Pedro, quero multiplicar por 5, tá bom? Multiplica por 5 em cima vira 15. E multiplica 0 2 por 5, ele vira 1. 15/ 1 já é o resultado. Entendeu? É isso. Tá pegou. Show. Então, quanto é 3/ 0,2? Essa é uma forma. É você
já visualizar e isso aqui, ó, 3/ 0,2. E você falar assim: "Eu quero retirar as vírgulas daqui". Então, para eu retirar a vírgula daqui, eu tenho que multiplicar esse cara por 10, né? Porque aí o 0,2 vai virar um do Isso aí. Multiplica ele por 10. Só que você vai ser obrigado a fazer a mesma coisa em cima e multiplicar por 10 em cima faz ele virar um 30. Agora sim, quanto é 30/ 2? 15. Entendeu? Perfeito. É, tá lá no alfabetização e matemática bem detalhado também para quem quiser ver mais sobre isso. Eu recomendo
mesmo que vejam, porque, né, vocês estão eh tem gente que tá precisando disso, tá bom? Vamos lá, então. 3 di por 0,2. Aqui a resposta é 15, tá? Eu tenho três coisas para 0,2 pessoas. Então, pensa assim, ó. Numa sala tem 0,2 pessoas, tem três coisas. Então, a pergunta é: quantas teria para cada uma delas? Mas tem 0,2. Mas e para cada uma, pô? Para cada uma tem uma é cinco vezes mais pessoa que tem, então cinco vezes mais coisa também, tá? Beleza? Quanto é 24/ido para 0,3? Então, toda divisão, ela vem com essa resposta
de quanto que cada um ganha, entendeu? Então, quanto que cada um ganha? Você tem 24 para 0,3 pessoas. E se for para uma pessoa, né? Eh, só para te mostrar aqui, tá? Eu vou, não é para fazer desse jeito que eu vou fazer, é só para mostrar um pouquinho de uma lógica aqui, tá bom? Eu quero dividir em cima e embaixo por três. Posso fazer isso? Vou dividir por três aqui. Vou dividir por três aqui. Tá bom? Faz comigo. Quanto é 24/ 3? É 8. E 0,3/ 3 é 0,1, né? Se eu tenho 0,3, eu
vou dividir por 3, fica 0,1. Agora sim. Vamos multiplicar por 10 em cima e embaixo, ó. Multiplica por 10 em cima dá 80. Multiplica por 10 embaixo dá 1. Então dá 80. 80/ 1 seja 80. Tá? Quando a gente encontra essa resposta nesse formato sobre um, é porque essa já é a resposta, tá bom? Beleza? Show. Agora mostrar um jeito assim um pouquinho mais ágil, né? Tu tem 24 div por 0,3. Tu multiplica por 10 em cima e por 10 em baixo direto. Então fica aqui 240, né? Porque aparece um zero aqui e aqui embaixo
a multiplicação por 103. 240 por 3 dá 80. Tá bom? Perfeito. Dá 80 a resposta aqui da segunda dessa, desse próximo desafio. Tá bom? Show. Ã, então vamos lá. Quanto é 08 + 08 + 04 - 1? É, aqui já entrou até um número negativo aqui, né? Então vamos lá. 08 + 08 dá 1,6 + 04 dá 2, né? 1,6 + 04 dá 2. - 1 dá 1, tá? 3 + 27 dá 30 + 18 48. 48 + 0.01. Caramba, vai dar com certeza 48, né? Vrul qu. Concorda? Tá errado. V01. OK. 48,01. Beleza? Então,
eh, e se fosse menos, seria 47,99. Perguntaram aí. Se fosse menos seria 47,99. Tá? Por quê? Porque eu tô aqui com, olha só, você pensa comigo aqui, ó. Cheguei no 48. Se eu falar para tu quanto é 48 + 1, tu a resposta vai ser o quê? 49. Se eu falar quanto é 48 + 10, então a resposta vai ser o quê? 58. Tô somando aqui 10, né? Então vai pular aqui uma uma casa decimal, né, de dezena. Tô somando agora um. vai pular uma unidade inteira do 48 pro 49. Agora eu tenho 48, eu
estou somando 0,1. Não vai chegar a pular uma unidade, não vai pro 49, vai continuar no 48, porém aumentou um pouquinho. Agora 48 + 0.01 vai ficar o quê? 48,01, entendeu? Agora 48 + 0,001 vai ficar menor ainda. 48 vai crescer pouquinho, mas 0 48,001. OK? Beleza. Quanto é? 0,001 mais 0. Tá bom? Vamos dar uma olhada aqui, né? Eu tô vendo aqui já que todo mundo tá com três casas decimais, né? Todo mundo aqui está com três casas decimais, né? Então, legal. Eu vou só somar isso aqui normalmente, né? Então, aqui, ó, 0,001 +
esse 0.001 dá 0.002. Aí com esse 0.002 já tem 0.004. Aí com esse 0.004 aqui vai ficar 0.008, tá? Só para deixar claro, até aqui, até aqui eu tenho 0.008, tá bom? Até ali. Agora eu tenho que somar com essa última aqui, 0.7. Quanto que dá isso? Tá 0,00 15, certo? A galera erra muito isso aqui, muito, mas muito mesmo, tá? Olha como que não faz sentido isso aqui. Eu quero só que você veja como que isso aqui é um absurdo, né? Você tinha 0.008 008 + 0.007. Agora tu tem 0.001. Como é que você
somou duas coisas e ficou ainda menor? Ó, 0.00 e aí na terceira casa decimal 8. 0,00 na terceira casa decimal 7. Aí agora 0. Na terceira casa decimal 1. Como assim, né? Como é que você, na verdade, essa casa aqui não vai aguentar, né? 8 + 7 vai dar 15, né? Para onde que esse 15 vai? Vem um para cá, para trás, né? Esse 15 aqui vai ficar um aqui e o cinco aqui, né? Então a a verdadeira resposta não é essa daqui, né? Eu vou até escrever aqui embaixo, ó. É 0.015, se quiser completar
com zero para enxergar, né? Eh, só para deixar mais claro aqui ainda, se você pegar esses números aqui, ó, 0.008 + 0.00 007 e você completar eles com zero, você não vai mudar nada no valor deles, mas talvez você enxergue melhor aqui, ó, 0. 070. Talvez você enxergue melhor agora, tá? Que isso aqui tem que dar 0.0 150, tá bom? Então aqui, ó, eh, eu tô somando 0.0080 com 0070 isso tem que dar o quê? 0, tem que dar 050, entendeu? Começando aqui já na terceira casa, beleza? É assim como deu aqui, tá bom? Mas
é melhor dizer, né? O jeito mais assim, mais compacto é esse aqui, né? É você saber que 0.008 + 0.007 dá 0.015, tá? Ficou maiorzinho. Beleza? A letra O é simples. Ô, Natália, aqui, ó, 08 + 08 dá 1.6, concorda? 8 + 8 daria 16, né? 08 + 08 já vai 1,6. Aí bota o 0,4, já tem 1,6 + 04. Você fechou ali, né? Você tem aqui 1,6 mais o 0,4. Você vai ter aqui o dois, né? Pode somar assim também, ó. 4 + 6 dá 0, sobra 1. Agora 1 + 0 daria 1. Com
aquilo ali dá 2. Aí bota vírgula embaixo da vírgula. Na soma e na subtração é tudo certinho, tá? Na soma e na subtração é tudo certinho, tá? Você só bota para se fazer soma e subtração, você tem que botar vírgula embaixo de vírgula e depois repetir a vírgula no resultado, tá? Eh, então aqui dá resposta 0,15, não, 0,015. Se eu botar 0,15 ficou enorme, né? Ficou muito maior. Tá bom? Eh, só para vocês visualizarem assim como é que, deixa eu colocar uma aqui, ó. Essa aqui de baixo, tipo, né? Como é que arma essa conta
se você quiser armar? Ó, 0,19 mais 0,01. Claro que dá 0,20. A gente já tá vendo, né? Mas assim, ó. 1 + 9 dá 10. Boto o zero aqui. Agora 1 + 0 dá dá 1 com aquele com aquele um que sobrou, né? Fica dois. Vírgula embaixo de vírgula e zero aqui. Tá bom? Então 0,20 aqui a resposta. 1,56 + 29. Essa daqui foi muito boa, né? Foi para pegar muito vocês, né? Aqui dá 30,56, né? Eu tenho 29 coisas inteiras. Aí eu boto mais uma coisa inteira, já começa por aí. Quando eu boto uma,
vai fechar 30. Aí agora eu tenho 30 e tenho 0.56, né? 47 - 0.03. Se fosse 47 - 3 daria 44, né? Se fosse agora 47 - 03, aqui, ó, só para escrever para vocês, 47 - 0,3, daria o quê? Tu rompeu uma unidade, né? Então tu teria 46,7. 46,7 se fosse -03, tá? Você rompeu a imunidade, você arrancou 03 dela, mas sendo 47 - 0,03, aí nesse caso, tu não vai tu vai romper uma unidade, vai, tu vai ter 46, mas tu não vai cair para 46,7, tu vai continuar com 46,9, porém 97, entendeu?
Você rompeu, mas você não chegou nem a, você não chegou nem a arrancar 0,1, né? Porque quando tu arranca 0,1, você fica com 46,9. Tu arrancou 01 aqui, tu não arrancou 01, tu arrancou 0.03, é menor do que 01. Então tu vai continuar com 46,9, mas tu vai quebrar essa última casa aqui. Ficou legal? Ficou claro? Mas eu vou mostrar um negócio agora aqui bem interessante, né? Que isso aqui vai complementar muito o aprendizado, que é o seguinte, Pedro. Como é que eu armaria essa conta aqui? 47 - 0,03. Como é que eu armo isso
aqui? 47 men. Eu falei o quê? Vírgula embaixo de vírgula. Lembra disso? Eu disse isso para vocês, né? Falei, olha, vírgula embaixo de vírgula. Então, 47, cadê a vírgula do 47? Ah, não tô vendo. Então, ela tá aqui na frente, né? 47,00. Não muda nada, concorda? Não muda nada, certo? 47,00 é a mesma coisa que 47. Aí agora eu pego aqui, ó, e boto 0,03, vírgula embaixo de vírgula. Agora eu faço essa subtração, tá? Como é que eu faço a subtração do três para chegar até o zero? Falta quanto? Opa, não dá para fazer, né?
Porque o porque o como é que três vai chegar até zero? Zero é pequeno. Então eu vou fazer três para chegar até 10. Só que por eu ter que fazer isso, esse é o meu jeito de fazer, tá bom? Eu não faço negócio de peg emprestado, nada disso, não, tá? Eh, olha só, eh, do três para chegar até o zero não dá. Então, finge que o zero é um 10. Ah, quanto que é do três para chegar até o 10? É 7. Mas por eu ter feito isso, eu aumento um aqui embaixo, tá bom? Então,
agora eu vou falar assim, ó. Agora aqui virou um. Aqui embaixo virou um, tá bom? Então agora do um aqui embaixo para chegar até o zero não dá. Então o zero vai ter que virar 10. Do um para chegar até o 10, falta o quê? Falta nove. Só que aí eu aumento esse cara aqui. Do um para chegar até o sete, falta quanto? Falta seis. Vírgula embaixo de vírgula, tá? E aí eu não, eu não aumentei esse aqui não. Ele é o sete mesmo, não mudei nada. Então aqui embaixo não tem ninguém. Do zero para
chegar até o quatro falta quanto? Falta quatro. 46,97. Eu ensinei assim lá no alfabetização matemática. Tá bom, Pedro? Resolve para mim como que você faria a seguinte conta. 46,97 x 0,03. Cara, como que eu faria mesmo? Tô só querendo ver como é que eu faria na hora da prova. Pô, bicho, vou ser sincero, essa conta aqui eu armaria. Essa conta aqui eu armaria mesmo, tá bom? Tem várias formas de fazer, tem notação científica, tem uma série de formas, tá? Não, então quem quer, alguém aqui quer saber esse método de subtração que eu acabei de mostrar,
que é melhor do que aquele métodozinho de botar coisinha? Então, assiste a aula lá da do alfabetização matemática que eu vou botar dentro do ciclo para vocês verem, porque já tá explicado lá, entendeu? Então lá eu expliquei tipo tantã mesmo assim de tieteca, expliquei, olha que subtração, faz assim, eu armei todas as continhas bonitinhas, tá bom? Eu vou botar hoje para vocês lá na sequência que vocês tem que assistir dentro do módulo do ciclo para vocês não terem que ir lá no alfabetização, beleza? Já tem, né? Acho que eu já botei hoje. Já botei hoje,
né? Já coloquei, né? Aí tá lá. Já já botei como é que faz isso. É isso aí, né? ali um monte de gente falando que já assistiu, já assistiu, já assistiu, entendeu? Eh, só para vocês saberem, tá bom? A galera tá muito engajada, os relatórios estão absurdos, tá todo mundo assistindo muita coisa, então não fique para trás, tá bom? Então, como é que eu faria essa conta aqui, cara? Se eu quisesse muito fazer de cabeça, vamos fingir que eu quero muito fazer de cabeça, invés de fazer 0.03, eu ia fazer vezes 3 e depois no
final do resultado, só vou, eu sei que eu ainda não ensinei isso, mas eu vou deixar aqui o 10 a -2, tá bom? Eu só vou puxar duas casas para trás, tá bom? Porque não era para ser 03, era para ser 0,03. Então, o resultado final eu vou dividir por 100, eu vou puxar dois casos para trás, tá bom? Agora eu vou fazer 3 x 47, só que como eu aumentei 0 p e eu aumentei 0.07, eu aumentei 0.21, eu vou tirar 0.21, entendeu? Então, 3 x 47 daria 120 + 21 daria 141 - 0,21
daria 140 [Música] ã79 e ainda dividido por 100 daria 1,479. Essa é a resposta. Acho que é essa a resposta mesmo, né? Aí essa mesmo, né? Mas isso aqui é porque eu, né, eu não recomendo fazer assim de forma alguma, tá bom? Porque eu acho que até eu na hora da prova não teria feito desse jeito que eu fiz agora, porque é um jeito muito avançado. Vou te dizer como que você realmente deve fazer essa conta aí absurda que propuseram aí na hora da prova, tá bom? Se na hora da prova você se depara com
46,93 x 0,03, se você se você tiver já a confiança e eu acho que e você vai ter semana que vem, porque eu vou ensinar isso, você invés de fazer vezes 0,03, você faz xzes 3 e depois você faz xes 10 a 2. O 10 a -2 é só para indicar, galera. 3 x 10 - 2 é a mesma coisa que 0,03, tá bom? O 10 a -2 é um indicativo aqui de que você vai puxar duas casas para trás, tá bom? E aí, como é que você faz o três vezes isso aqui? Você ainda
assim arma conta. Você faz assim, ó. Ó, deixa eu pegar aqui para ficar bom para todo mundo ver. Ah, vou botar aqui embaixo, ó. Você arma uma continha aqui, ó. 3 x 3= 9. 3 x 9 27, so 3 x 6 18 com aqueles dois, dá 20, so 2. 14. Duas casas decimais aqui em cima, não é isso? Então, duas casas decimais. Agora tem que multiplicar por esse 10 a - 2. Ele vai fazer voltar ainda mais duas casas. Então, na verdade fica 1,479. É rápido e é seguro e é garantido, tá? Beleza? E ainda
tem outras formas de fazer, tá bom? Que é você agora você pegar esse cara aqui, ó, e você aumenta ele 100 vezes. Então você tira a vírgula daqui e pronto, ele tá 100 vezes mais. Você vai falar assim: "Ué, aumentou 100 vezes?" Então, aí você, como tu aumentou ele 100 vezes, tu bota um contraponto de -1 para diminuir ele. Ou seja, o -2 vira -4. O 10 a -4 aqui agora, ele carrega quatro casas desse mais para trás para compensar isso aí. E aqui tu já consegue fazer de cabeça se tu quiser, tá? 3 x
4693, né? Você já consegue fazer 3 x 4700 e remover 21, tá? Aí 3 x 4700 dá 12.000 + 2100. 14.100 - 21 dá 14.079. Aí 14.079 x 10 a - 4 indica que tem 1 2 3 4 0,1479. Tá? Mas aí é semana que vem a gente vai pegar bem notação científica. Vocês vão ficar bem espertos com isso. 47 - 0.03 dá o quê? 46,97. Tá beleza? OK. Eu viram alguém tá incomodado que eu deixei a última resposta de rosto e todas outras de vermelha. Isso aí incomoda o toque de alguém. É, as meninas
estão pedindo, bota vermelho, então tá bom, só para não, tá? Vamos lá, então. Show. Foi isso, tá bom? Essa aí foi a nossa aula de números decimais. Agora a gente vai pra próxima. Valeu, galera. Tamos junto. Vamos nessa. Sejam todos muito bem-vindos a mais uma aula da plataforma SAD. Eh, agora a gente vai dar continuidade aqui ao nosso estudo, né? E o que a gente vai fazer agora é entrar no assunto dos múltiplos, tá? Então, a gente vai fazer agora aqui o assunto dos múltiplos e dos divisores, beleza? Então, assim, vamos lá, vou dar a
definição teórica aqui, tá bom? Tanto dos múltiplos quanto dos divisores, beleza? Vamos lá. O que que é múltiplo? Múltiplos são todas as consequências possíveis de você pegar um número e fazer a multiplicação dele por outros números naturais, tá? Só para deixar claro, que que é número natural? número natural são aqueles números eh, exatamente, são os números aí que existem. Eh, só é óbvio que todo mundo já ouviu falar disso, mas eu quero deixar assim bem claro. Qual você acha que são os números? Quais você acha que são os números naturais? Os números que existem na
natureza. O próprio nome diz, né? 1 2 3 4 5 6 7 8, né? Na natureza aparece o número 7,67? Claro que não. Não é natural. Na natureza aparece, não. Falaram os algarismos, não. Tá errado, tá? Na natureza aparece os números eh 0.03. Claro que não, pô, né? Isso aí é uma coisa da construção mental do homem, né? O que aparece na natureza é o quê? Uma banana ou duas bananas, né? Ou três bananas. Agora, o cara olhar pr metade de uma banana e falar: "Isto aqui é 0.5 banana", isso não é uma coisa natural,
tá? Não existe. Exatamente. Não existe 6.44 porcos. Não tem isso. É isso aí, né? Tem seis porcos ou sete porcos, tá bom? E também não existe menos quatro porcos negativos. não tem porco negativo, tá? Então os números naturais eles são todos os números inteiros, então não tem número quebrado, tá? E positivos, tá? O que que são os múltiplos de um número? São as consequências de você pegar esse número e multiplicar ele por todos os números naturais, tá? Mas também pelo próprio zero, tá bom? Ou seja, vou deixar bem resumido aqui. O que que são os
múltiplos? O múltiplo de um número, a tabuada daquele número, como se fosse as possibilidades. Deixa eu deixar bem claro aqui, tá bom? Quais são os múltiplos de três? Vamos escrever aqui agora os múltiplos de três. Beleza? Primeira possibilidade é eu sempre fazer 3 x 0. E quanto dá isso? Zero. Então zero é múltiplo de todo mundo. Próxima possibilidade fazer três vezes quem? Depois que eu fiz 3 x 0. 3 x 1. Ó, isso aqui cai, tá bom? Sabe onde é que essa isso aqui cai? Em análise combinatória, em probabilidade, tá? Então olha só, quanto é
3 x 0. É uma possibilidade 0 e 3 x 1 é 3. Pronto. E agora? Agora qual é a possibilidade de fazer 3 x 2? 3 x 2 dá 6. E se for 3 x 3, 9. Aí assim vai. 3 x 4 dá 12, 15. Múltiplos são isso. Todos os possíveis resultados de você pegar esse cara aqui e multiplicar ele pelo zero, pelo pelo 2, pelo três, pelo 4, tá? Então, quais são os múltiplos de sete? Bem, eu posso começar com 7 x 0, isso vai dar zero. Depois 7 x 1 vai dar 7. Então,
todo número começa com os múltiplos zero e ele próprio. 7 vezes alguma coisa vai dar, por exemplo, 3,5. Sim, 7 x, mas aí o 3,5 não é um múltiplo de 7, porque eu falei que é tu pegar o sete e multiplicar ou pelo zero, ou pelo um, ou pelos números naturais em diante, tá? Então por isso que não não existe isso, entendeu? Então são só as respostas exatas inteiras, tá bom? Então 7 x 0 dá 0, 7 x 1 dá 7, depois dá o quê? 14, 21. Esses são os múltiplos do 7, tá bom? Deu
para entender? É. É, e assim já vou deixar aqui claro um conceito, né, que é o conceito de de deixa eu colocar aqui para ficar bem bonito pra gente, né? Vamos pegar assim, ó. Quais são os múltiplos de três, né? Ali estão viajando, já tô perguntando, mas o sete não é primo? Mas primo não tem nada a ver com isso. Primo é o número que ele é divisível apenas pelo um e por ele mesmo. O sete é primo porque você só consegue fazer uma divisão exata do sete por quem? 7/ 1 que dá exato, dá
o próprio 7 e 7/ 7 que dá 1. Isso é um número primo. Um número primo é aquele número que você só consegue dividir ele por um e por ele próprio, tá? Então oito é um número primo. Vamos lá. Dá para dividir o oito por um? Dá dá oito. Dá para dividir o oito por ele próprio? Dá dá um. Mas o problema é que também dá para dividir o oito por dois, né? Que dá 4 e também dá para dividir o 8 por 4, que dá dois. Então ele não é primo, porque o primo é
aquele que só pode ser dividido por um e por ele próprio. Tá bom? Só para você entender, os números primos eles são os blocos de construção de todos os números do mundo, tá? Os números primos eles são aqueles que são podem ser usados para construir qualquer número. Beleza? Sacou? Eh, é isso aí. Os múltiplos eles são as possibilidades de resultado, tá bom? É, cara, todo número ele pode ser construído por números primos. Todo, tá? Até que tem que ler a apostila. Acho que vocês não leram a apostila porque eu botei isso na apostila bonitinho, tá?
Então, vamos lá. Vamos falar os múltiplos aqui de de três, né? Então aqui, ó, é tanto aqui o zero quanto aqui o zero, né? Beleza? Do se e do e do três, né? Mas vamos próximos dar o zero. Ele tá aqui, mas ele não conta de verdade, né? Ele conta, mas não não serve para nada saber disso. Agora, quanto que dá 3 x 1? Dá 3. E 3 x 2 6. E 3 x 3 9 12 15 18 vai 24 27 30 concorda? 33. Tá. E agora os múltiplos do 6. 6 x 0. 6 x
1 6. 6 x 2 12 18 30 36, né? 6 x 6. 6 x 7 42. Legal. 48. Tá. Se eu te perguntasse agora, né? Eh, me fala aí um múltiplo que eles tenham em comum. Fala um múltiplo em comum. Tu vai olhar assim, ah, pô, o 36, eles dois tm 36. né? Os dois têm esse múltiplo, né? E o um. Então, para outra assim, o cara seis vezes o que que dá um e três vezes o que que dá um? Me responde. Três vezes o que que dá o resultado um? Entendeu? 6 vezes o
que dá um? Eu falei que os múltiplos eles são as respostas, né? Tá. Cadê outro múltiplo em comum deles? Pô, 18. Os dois têm esse 18 aqui como múltiplo, né? Claro que de formas diferentes, né? E outro múltiplo em comum deles, o seis. Perfeito, né? Outro múltiplo em comum deles, o 12. Outro múltiplo em comum, o 24. Os dois têm o 30, os dois t. Eles têm vários múltiplos em comum. Vários, né? Qual é o mínimo? Qual é o menor múltiplo comum? É o seis. É o seis, tá? Isso aí serve às vezes quando eu
tô somando ali uma fração, né? Eu tô ali somando assim, ó. Eh, não, o zero não conta nisso porque o zero não vale, tá? O zero é múltiplo de todo mundo. Então, olha só, quando eu tô aqui com eh pô 2 sobre 3, eu quero somar isso aqui com 1 sobre sobre 6, né? Qual é o mínimo múltiplo comum entre eles? É o seis. Então, assim, meu objetivo é transformar esses denominadores na mesma coisa. Eu quero fazer com que eles sejam iguais. Cara, eu posso, por acaso, você acha que vai dar certo, pô? Se eu
fizer, ah, vou transformar eles na mesma coisa, então vou transformar os dois em 30, porque eles dois têm o múltiplo 30. Você acha que isso vai dar certo? Transformar os dois em 30, né? Claro que vai dar certo, não tem problema nenhum você fazer isso. É óbvio que vai dar certo, Tá maluco, né? Ah, eu quero que os dois sejam 30. Tá bom, vamos lá. Olha para essa primeira fração. Como é que eu faço para esse denominador virar 30? Eu multipliquei ele por 10. Então, em cima eu também multiplico por 10. E como é que
eu faço para esse cara virar 30? Nessa fração aqui agora eu multiplico ele por cinco. Concorda? Ele virou 30. Em cima eu multiplico por cinco também. Beleza? Agora eu faço a soma de frações. Repete o denominador que já tá igual e soma aqui. 25/ 30 é a resposta, tá certo? Mas é muito melhor, é muito menor, é muito melhor eu fazer com o mínimo múltiplo comum. Para que que eu vou transformar os dois em 30 se o mínimo múltiplo comum entre eles é o seis? Então é melhor se eu pegar esse três aqui e transformar
ele em seis. Então eu duplico ele em cima também eu duplico, né, para manter igual. Agora que eles estão iguais ali, eu faço 4 + 1, 5.6 é a resposta da mesma forma que 25/ 30 é a resposta. Isso é a mesma resposta. Ai Pedro, como assim? Eu pego essa fração aqui, eu vou dividir por cinco em cima e embaixo. Divid por cinco em cima vira cinco. Divide por cinco embaixo vira seis. Pronto, mesma resposta. Só que é melhor para mim que eu utilize o mínimo. Isso tá explicado perfeitamente nas aulas que estão lá no
ciclo de nivelamento intelectual, tá bom? Nas aulas teóricas que eu botei lá do alfabetização. Não vai achar pagar de doido, não. Achar que aquelas aulas ali são velhas, aquelas aulas foram gravadas há pouquíssimo tempo, elas estão ali perfeitas, tá bom? Por isso que eu coloquei ali, tá? Aquelas aulas ali estão ótimas. É para justamente para vocês assistirem, tá? Isso aqui que eu tô fazendo é carga de exercício maior ainda para vocês, tá? Então, pronto. Agora, o que que são divisores? Divisores agora é o contrário. Múltiplos são as possíveis respostas de um número sendo multiplicado pelo
zero, pelo um, pelo dois. Beleza? Divisores é o quê? É o que que são os divisores de números? São os números pelos quais dá para eu dividir aquele número e a divisão vai dar exata, tá? Então, por exemplo, quais são os divisores de 10? É, são os números que eu posso pegar o 10 e dividir por eles e vai dar exato. Por todo número, o primeiro divisor dele vai ser sempre quem? Um. Porque eu posso sempre pegar o número 10 e dividir por 1 e vai dar exatamente 10. Eu posso dividir o 10 por 2
e dar certinho? Sim ou não? Sim. 10 dividido por 2 dá certinho. Eu não quero a resposta aqui de quanto é 10 por 2. Eu quero saber se, ó, olha o nome, olha o nome. Vem pelo nome. O dois é um divisor do 10. Ou seja, eu consigo dividir o 10 pelo 2. O o dois ele é capaz de ser um divisor pro 10. Eu não tô querendo o resultado da divisão, tá? Agora, e o três? O trê é um divisor do 10? Claro que não, pô. 10/ 3. Dá para fazer essa divisão? Essa divisão
por acaso tem resposta? Claro que tem, pô. 10/ 3 é 3,33, né? Só não é exata. O conceito de divisor é quem divide exatamente, tá? Só isso que é o problema. Beleza? Mas dá para fazer a divisão, dá 3.33, né? Mas eh ainda não tá exato, né? É 3,33 e fica indefinido, né? Tu vai ficar dividindo aqui, tu sempre vai conseguir detalhar um pouco mais, mas vai ficar irrelevante. Então o três não é um divisor aqui. E o 4 é um divisor também não. 10/ 4 dá 2,5. Não dá exato. 2,5 não é um número
inteiro, né? E o o 5 é um divisor. O 5 é 10 por 5 dá exatamente 2. E o se é um divisor, não é? O sete é um divisor, não é? O oito é um divisor, não é o nove, o divisor não é o próximo divisor o 10. O último divisor de um número é ele próprio, né? O último é ele próprio sempre, tá? Porque dá para tu dividir ele por um, vai dar certinho. E se tu dividir ele por ele próprio, vai dar um. 10 por 10 dá 1. Mas entre eles ali pode
ter gente ou não. Se não tiver ninguém, se ele só tiver o um e o 10 é porque ele é primo. Então, por exemplo, 7 dá para dividir 7 por 1? Dá um 1 é divisor por 7. Por 2 dá? Claro que não. 7 por 2 é 3,5. Por 3 dá não. 7/ 3 é 2,33. Dá para dividir o 7 por 4? Dá, mas não vai dar exato. 7/ 4 vai dar 3,5 1.75. 7 dá para dividir por 5 vai dar 1,4. Não é exato. 7 dá para dividir por 6 vai dar 3,5. 3,5 divido
por 3 vai dar 1,16. Não dá exato. 7 dá para dividir por 7. Dá, isso aqui é um número primo. O sete, você não tem blocos constitutivos que montem ele. Você não consegue montar o número sete, multiplicando o número. Você só consegue montar o sete com o próprio sete. O número primo, ele não pode ser montado por outras outras combinações. Por exemplo, o 10. Eu consigo pegar o 10 e representar o 10 por quem? Olha isso aqui agora. Para tu entender o número primo de verdade. Eu posso escrever o 10 como sendo o quê? 2
x 5, eu consigo montar o 10 usando isso, né? Ele ele pode ser montado assim, ele pode ser montado como 1 x 10, né? E só não é números ímpares, não. Por exemplo, o nove é um número ímparo. O nove não é primo. O nove pode ser escrito como sendo o 3 x 3. Mas é óbvio que ele também pode ser escrito como 9 x 1, entendeu? Não tem nada a ver com isso não. O 15 é um número primo. Não, 15 não é um número primo, ele é um número ímpar, né? O número, o
15 é um número ímpar. Ele pode ser escrito como sendo 3 x 5, ele pode ser escrito como sendo 15 x 1. Ele pode ser montado dessas duas formas, né? O 25 é um número ímpar, ele pode ser escrito como 5 x 5. Nenhum desse aqui é primo. O primo é um número que ele só pode ser dividido, você só consegue quebrar ele ou dividido por um ou por ele próprio. Entendeu? Eh, você pegar, por exemplo, número, sei lá, pegar aqui um exemplo bom para mostrar isso que eu quero. Número 45, por exemplo. É óbvio
que ele não é primo, ele pode ser dividido pelo um, pode ser dividido pelo 45, mas ele pode ser dividido por três, ele pode ser dividido por 5, ele pode ser dividido por 15, ele pode ser dividido por várias coisas, pode ser dividido por 9, né? O 45 ele pode ser montado de ali moleque falou assim: "Pedro, você tem noção de que a gente tá em novembro e tu tá aprendendo 400 pessoas na aula até 9 da noite?" Maneiro isso aí mesmo. A gente vai arrebentar. Então, olha só, o 45 eu posso escrever ele como?
Vamos lá. Vamos escrever primeira coisa, os divisores do 45. Pode ser? Vamos lá. Vamos lá. Vamos escrever os divisores do 45. Eh, um é divisor dele, três é divisor dele, né? Você consegue dividir 45 por 3 e dá exatamente 15, tá? 5 é divisor dele. Você pode dividir 45 por 5 e dar certinho, vai dar 9. Eh, 6 não é divisor dele. 7 não é, tá? 9 é 45/ 9 dá 5, tá? Ã, 10 não é, 11 não é, 12 não é. Perfeito. 15 é. Tá, falaram ali 30. Claro que não. Você consegue fazer 45/
30? Claro que não, pô. 45/ 30 vai dar 1,5. 1,5, tá? O próximo é o próprio 45. Tá? Então, ou seja, você consegue montar, né? O zero não é o zero é nulidade, o zero não é nada disso não. O zero não é primo, não, tá? Olha só, eh, a definição de prima é que ele pode ser dividido por um e por ele mesmo, tá bom? Nem o próprio um é primo, tá? Então, olha só ali, como que eu sei quais são os divisores? Me responde você agora. Fala você agora. Que que são os divisores?
Eles, os divisores são os números que conseguem dividir esse cara aqui sem deixar nenhum resto. Então é assim que tu sabe os divisores tu analisa e se pergunta: "Dá para eu dividir esse número por esse cara aqui sem ficar resto?" "Ah, dá." Então ele é um divisor. Não tem um um macete que eu vou te falar assim: "Ah, é só você pegar". Não, pô, isso aqui tem que analisar os divisores, entendeu? Eu quero muito que vocês tenham cuidado com essa mentalidade, hein? Eu é porque eu tô tô falando com com carinho e gentileza, mas eu
conheço esse tipo de pergunta. Como é que eu sei quais são os divisores de um número? É, entende? Você tá querendo disel de alguma forma? É um macete, uma coisa assim, não é? É tabuada. Você percebeu? É tabuada. É automático. A gente sabe pela tabuada. Tem que treinar a tabuada. Tem que treinar o, né? Tem que treinar o a visualização, entendeu? Tem que pensar. Dá para dividir. Então, como é que eu vou fazer para te dar um macete para tu saber os divisores de 90? Não tem. Tem que falar assim: 90 dá para dividir por
um? Claro que dá. E por dois? Dá. 90/ 2 dá 45. E 90 por 3. 3 é um divisor de 90. É. 90 por 3 dá 30. E por 4? 4 não. 90 por 4 vai dividir por 2 vai dar 45. Vai dar 22,5. Isso aí não é exato. E por cinco, por cinco dá todo mundo que termina em zero, né? Tá, tá lá no no ciclo de nivelamento de critérios de divisibilidade, né? Aqui é dividido por cinco. Beleza? E aí? E por 6? Dá para dividir o 90 por 6? Vai dar certinho? Cara, dá.
Dá sim. 90 por 6 dá exatamente 15. Eu consigo visualizar. Eu pego o 90, eu visualizei ele como 60 e o 30. Tanto 60 dá para dividir por 6 dá 10 e o 30 também dá 5. Então, beleza, dá para dividir por seis. O se é um divisor. E por sete? Por sete não dá, né? E por 8, por 8 também não vai dar. Não dá para dividir por 8. 80 div por 8 já vai dar aqui e 10. Aí tu vai botar 80. O próximo divisível é 88. Então o 90 não vai fechar, né?
A tabuada do 8 é o quê? 72 80 depois 88 depois 96. O 90 não entra. E por 9? Por 9 dá. 90 divido por 9 dá exatamente 10. E por 10, por 10 também dá certinho. O 10 é um divisor do 90. 90/ 10. Perfeito. E por 12? Tenta pensar. 90/ 12. Será que essa divisão funciona? Pega 90 por 12, simplifica. Divide por 3 em cima e em baixo fica 30 di por 4. Não dá. 30 por 4 vai dar 7,5, tá? Por 13 não precisa nem pensar muito, né? 13 é claro que não
dá. Por 14 também não dá, né? Por 15. Por 15 dá, né? Você visualiza 15, 30, 45, 60, 75, 90. 90 di por 15 dá o 6. Por 16 não vai dar. Por 17 menos ainda. Mas e por 18? Por 18 dá. 90 di por 18 dá 5. O 90 ele é 5 vezes o número 18. O 90 é 5 vezes o número 18. 18 36. Agora bota mais 18. Bota 20, tira 2. 36 56 54. Bota mais 18. Agora bota 20, tira dois para botar o 18. 54 74 72. No 72 você bota 18.
Encaixa certinho. 8 depois 10 fechou 90. Cinco vezes. Entendeu? Sacou? Como que multiplica por cinco de cabeça? Pode multiplicar por 10 e dividir por 2, tá? 10/ 2 é 5, tá? Por 20 dá, não dá. Aí vai chegar uma hora que você vai começar a perceber, por 20 não dá, certinho. Por 21 não vai dar, né? Você começa a perceber que não dá para tu pegar o 20 e tu agrupar até bater 90. Vai ser 20, 40, 60, 80, 100, né? E agora o próximo vai ser quem? Deve ser o 30. O próximo é o
30. 90 dá para dividir por 30. E o próximo agora é o 45. Não tem como você agrupar, porque olha só, tu tem o 30, tu consegue pegar 30 + 30 + 30 dá 90. Tu acha agora que o 31 vai ter como tu encaixar, tu fazer montar o 90 com ele? 31 + 31 dá 62 + 31 já dá 93 e assim vai. O próximo agora tem que ser o 45. Não sei se você consegue perceber isso, consegue visualizar, né? E depois do 45 vem quem? Cap 90. Entendeu? Vê agora como é que você
vai ficar olhando entre Não tem como você olhar. Como é que você vai olhar entre o 45 e o 90 se vai ter alguém? Claro que não vai ter. 90 dá para dividir por 45. Quanto que dá? Dois. Então, e agora? O próximo resultado possível é dar um. Então, 90 dividido por 90 vai dar 1. Se não o 45, tu pega o 45, tu faz o quê? Tu bota 2 45 90. E o 46 agora? Tu botar com 2 46 já vai pro 92. E o 47 tu já vai pro 94. É loucura. Só o
90 agora que vai funcionar, que é o 90 ali é o próprio resultado, entendeu? É, o penúltimo divisor de um número é sempre a metade dele. É isso aí, sacou? Pegou? Certinho? Então, beleza. Então, vamos nessa. Então, isso aqui são os divisores, tá bom? Aí é claro que o um ele é um divisor de qualquer número, né? Porque todo número pode ser dividido por um. Qualquer coisa você pode pegar e dividir por um. E aí você vai ver o resultado, né? E aí o próprio número também é sempre um divisor. Você sempre pode pegar um
próprio número e dividir por ele próprio. Então eu tenho 17. 17 ele pode ser dividido por 1. Dá 17. E 17 pode ser dividido por 17, né? Quando você divide o 17 por 17, aí dá um, no caso. Beleza? OK. Beleza. Eh, cara, essa regra aí, né, que eu falei de que o moleque perguntou assim: "Ah, então o penúltimo ali é sempre a metade?" Não, não é sempre que isso se aplica, não. Acabei de perceber. Claro que não. É só nesse caso aqui que, né? Só em alguns casos, né? Acho que se, se o número
for par, aí sim, né? Se o número for par, tem que ser, né? É, se o número for par, tá? Então, por isso que eu não eu não gosto dessa dessa quando o número for par, né? Eu esqueci de falar isso, tá? Cuidado aí com isso, tá bom? Show. Vamos agora agora concentrar aí. Então, a gente já tem as definições, tá bom? E aí, que que eu ia falar para vocês? Você viu de quantas formas o 45 pode ser montado? O 45 ele pode ser representado eh ele pode ser representado de várias formas, né? O
45 pode, você pode escrever que o 45 ele é 3 x 5 x 3, né? O 45 ele pode ser escrito assim, ó, 3 x 3 x 5. Ele pode ser escrito como como 5 x 9. Tudo isso aqui é o 45, mas o número primo você não consegue montar ele. Você só consegue montar ele com ele próprio. Ele ele é imontável. Você não consegue construir o número primo usando ã outros números sem ser ele próprio, tá? Mas para você construir qualquer número, você tem que usar números primos, entendeu? Então, por exemplo, você vai ver
que os números primos eles são blocos. A gente vai pegar isso daqui a pouco. A gente vai entrar em faturação de número primo. Deixa que eu falo isso daqui a pouco, tá bom? Primeiro vamos treinar o mais básico, vamos treinar divisores, tá? Que a gente faz tudo em ordem, tá bom? Então, olha só. Ã, escreva os 10 primeiros múltiplos positivos de cada número. Eu quero os 10 primeiros múltiplos positivos de cada número e do menor pro maior, sem pular nenhum, tá? Então, todas as respostas vão ter que começar aqui com zero, né? Todas as respostas
aqui vão começar com zero. Agora, vamos lá. Ele quer, eu pedi quantos aqui? Os 10, né? Então, 0 2 4 6 8 10 12 14 1 2 3 4 5 6 7 8 9 10. Beleza? O do 3 aqui também. 0 12 18 24. 1 2 3 4 5 6 7 8 9 10. O do cinco tá zero. Eh, pera aí rapidinho. Acho que os dev é isso mesmo, né? Eu botei positivos aqui, né? Então não precisa considerar o zero, né? O zero ele é um número justamente, né? Não é nem positivo nem negativo. Ele
é tô viajando, galera. Foi mal aí, tá? Então aqui teria que colocar mais um no final, beleza? Perdão aí, eu eu tinha esquecido que eu botei aqui nessa parada do positivos, tá bom? Um não conta, galera, vocês estão confundindo, tá bom? Porque o o um ele é um divisor de todo mundo, tá bom? O um ele não é um múltiplo, beleza? Então olha só, cinco, vamos lá. 5 x 1 é que dá cinco, entendeu? O múltiplo é o resultado, tá bom? Aí galera, vai 5 10 15 20 25 30. São todas as possibilidades do cinco
ser multiplicado. 4 5 6 35. Galera, eu vou fazer falando aqui, tá bom? Vamos lá. 10 20 30 40 50 60 70 80 90 100. Tá, vou botar só o 40 aqui, que para alguns pode ser mais complicado. 40, 80, 120, 160, 200, 240, 280, 320, 360, 400. Esses são os múltiplos, tá? Resultado do 40 multiplicado aí por pelos pelos números, tá bom? 40 x 1 dá 40 e assim por diante, tá bom? Se eu não tivesse falado positivo ali, aí seria para incluir o zero também, tá bom? Então aqui, ó, 200. Agora vamos lá.
Múltiplos do 200, 400. Cuidado para não sair dobrando, botar tipo 800 e tal, não é assim, tá bom? É para você ir botando de 200 em 200, tá bom? Então, olha só. Eh, qu aqui tem o próprio 200, né? Aí, depois do 200 vem o 400, depois do 400 vem o 600, tá? Depois vem o 800. Depois vem o 1000, tá? O 200 aqui tá incluso, tá bom? Só não escrever ele por causa do espaço. 1200, 10000 1600 1800, ó. 1 2 3 4 5 6 7 8 9 e até o 2000, beleza? Do 125,
tá? 125, 250, 125 x 3 agora, né? Vai botando mais 125 sempre que você vai conseguir acertar, tá? 375 agora 400 500 agora 625 agora 750 agora 875 agora 1000 beleza 1 2 3 4 5 6 7 8 aí 1125 e 1250 tá bom vamos lá aqui no caso do do set tá bom galera é para colocar o próprio número tá bom para colocar o próprio número porque eu pedi assim uns 10 primeiros múltiplos positivos. Então o próprio número entra nisso, tá bom? O próprio 125 entra nesse caso, tá bom? É só que aqui em
cima eu escrevi aqui, eu botei aqui só porque sei lá. Então aqui, ó, no múltiplos do sete agora, 7 14 28 35 42 63. Tá? Múltiplos do 12. Tirando o zero, né? Que nessa questão não cabe porque ele pediu positivo, ó. 12 24 36 48 72 84 96 108 120 beleza? Do 25 50 75 100 125 150 175 200 225 250 Beleza? Show. Todos os divisores positivos de cada número do menor pro maior. Agora eu quero todos, tá bom? Quem é o único divisor do um? Um. Só dá para dividir um por um. Quem é
o divisor do dois? Dá para dividir o dois por um e dá certinho. E pelo próprio dois também. O dois é primo. Isso aí. Quem são os divisores do três? 1 e três. O três é primo. Quando é divisível só por um e por ele mesmo é primo. Quem são os divisores do quatro? 1, 2 e 4. Sempre tem um e o próprio número. Ele não é primo. Tá bom? E tu vê que ele não é primo, significa que ele, quando ele não é primo, ele pode ser construído por uma combinação de outros números primos.
O quatro, ele pode ser escrito como 2 x 2. Você consegue construir o 4 com 2 x 2, tá? Ele é feito de outro número, tá? Agora você não consegue construir o dois e o três com outros números. Você precisa do próprio dois e do próprio três, tá? O cinco, um dá para dividir ele por um, então um divisor, né? Dá para dividir ele por dois? Não, por três, não, por cinco. Ele é primo. Vou tentar construir o cinco usando outros números. Impossível. Você não consegue construir o número cinco usando outros. Você, o cinco é
o próprio cinco. Você nunca vai conseguir chegar no cinco eh sem usar eh ele próprio. Você pode pegar 2 + 2 + 2, já virou 6. 2 + 2 virou 4. Aí se pegar eh você pegar multiplicando, né? Eu digo, não é somando, né? Eu tô falando, perdão, tô falando multiplicando. Você, se você pegar 2 x 2, dá 4. Dá 6. Você precisa, o 5, ele é um número diferente, ele é primo, tá? Eh, oito divisores dele, 1, 2, 4 e ele próprio, tá? E tu vê que o oito ele não é um número primo,
ou seja, oit ele poderia ser escrito, por exemplo, ah, Pedro, como 2 x 4. Sim, mas o 4 é 2 x 2. Então ele poderia ser escrito como 2 x 2 x 2. Ou seja, ele é construído por um número primo. Com o número dois, você chega no oito, tá bom? Beleza. Primo vem como se fosse de de de primeiro, tá bom? Show. Só um um instantinho aqui. Voltamos aqui. Então vamos lá. Quais são os divisores do número 15? Claro que ele pode ser dividido por um e dá exato. Ele pode ser dividido por dois?
Não, ele pode ser dividido por três? Pode. 15 por 3 dá certinho. A gente já sabe que ele não é primo, né? E por cinco ele pode? Cinco ele pode. E por 7, 8? Não, não pode, tá bom? Por 10 também não. Por 15 é ele próprio, tá bom? Ou seja, você vê que o número 15 ele pode, ele não é primo, né? E ele pode ser escrito como? Com números primos. Você pode chamar ele de 3 x 5, você tá escrevendo ele com fatores primos, tá legal? Eh, e o 16? O 16 ele pode
ser dividido pelo um, pode ser dividido pelo 2, pelo 4, pelo 8 e pelo 16. Tá bom? Tu vê que o 16 não é primo, ele pode ser escrito apenas como e você pode usar só fatores primos e você consegue escrever ele com 2 x 2 x 2 x 2. Beleza? Vamos lá. O sete, o sete ele já é um número primo, né? Ele só pode ser dividido pelo um e por ele mesmo. Tenta escrever o sete com um produto, você não consegue. O sete só pode ser escrito pelo próprio set, ele é um número
especial, tá bom? O 12. Quem são os divisores de 12? 1, 2, 3, 4, 6 e 12. Você pode dividir o 12 por todos esses números aqui e você vai conseguir e divisões exatas, tá bom? Tu vê que justamente o 12 não é primo. Como é que você poderia escrever o 12? 2 x 2 x 3. Ou seja, você consegue construir ele com números primos, tá? Ah, Pedro, mas eu consigo construir o 12 com 2 x 6, mas o 6 eu não posso quebrar em 2 x 3. Você consegue sempre, um número que não é
primo, ele sempre pode ser reduzido a números primos. Olha, isso que eu tô querendo te dizer. Todo número que não for primo, ele pode ser reduzido a somente números primos. Somente, e nenhum outro, entendeu? Então, ah, Pedro, mas o 12 ele pode ser escrito como o 12 ele pode ser escrito como 3 x 4. Não, cara, 3 x 4 você não tá escrevendo ele na forma mínima. O 4 mesmo, ele não é um número primo. Então, transforma ele em 2 x 2. Pronto, somente números primos. Se o número não for primo, ele vai, ele pode
ser escrito por números primos como produtos, tá bom? Beleza. 80. 80 é um número primo. Claro que não. 80 não é divisível só por um e por 80, né? 80 é divisível por 1, por 2, é divisível por 4, é divisível por 8, é divisível por 10, né? É divisível por 16. É, é divisível por 16. Você pode pegar 80, dividir por 16 e vai dar exatamente 5, tá? E esqueci de colocar aquele divisível por 5, mosquei aqui, né? 1 2 4 ele é divisível por 5, ele é divisível por 10, ele é divisível por
16, ele é divisível por 20, né? Então tudo são divisores dele, né? Isso aqui são divisores dele. Esqueci também o oito de novo, né? Pô, tô moscando demais, caramba. Tá aqui, ó. Botei aqui o oito. Agora ele é divisível por 16, né? Aí a menina vem me perguntar qual o método para você saber os divisores. até eu, se eu der mole aqui, eu perco um divisor, né? Eh, por 10, como eu tava dizendo, né? por 16, por 20, por eh, só para confirmar se não esqueci mais nenhum, né? Por 40 agora direto e agora sim
por 80, tá? Eh, não, então vocês viram como é que eu tô justamente que eu tô melhor agora, né? Eu tô eu tô agora vi um ser humano normal. Eu sinto sono 9:30. Antes eu tava aí até, né? Então, olha só, antes eu tava, antes eu tava cansado assim, rendendo um pouco de manhã, né? Agora eu tô normal, tô rendendo um pouco de noite. Então, olha só. Eh, aqui temos os divisores do 80. Que que acontece? O 80 não é primo, claramente, ele não é divisível só por por um e por 80, né? Legal. Então,
fala assim, Pedro, então quer dizer que o 80 pode ser escrito por uma multiplicação de números primos, né? Isso aí, Pedro. Mas como assim só de números primos? Só de números primos. Você é só precisa de número primo para fazer 80. Vamos lá. 2 x 2 x 2 já dá 8. Ah, Pedro vezes 10. É, mas o 10 não é primo. Então, transforma o 10 em 2 x 5. Acabou. Aqui temos o 80, somente escrito com fatores primos. 2 é primo e 5 é primo. 2 x 2 x 2 é dá 8. 2 de novo
dá 16. 16 x 5 dá justamente 80. Ou seja, todo número que ele não é primo, ele ele é feito de uma combinação de multiplicações de números primos, tá? 160, cara. Ele vai ter todos os divisores aqui. Eh, não, mas é, eu esqueci alguma. Tão falando ali, Pedro, você esqueceu. Não, apagaram o comentário, não esqueci nada não. Então, olha só, cara, o 160 ele vai ter todos os divisores que o tem, todos, né? Não tem porque ele ter eh mais divisores até aqui, né? Até então vai ter a mesma coisa. A única diferença é que
ele vai ter também ele próprio, tá? Então o 160 ele tem todos os divisores aqui iguaizinhos, tá bom? Dá para dividir por um, por dois, por qu o que que é o 160, tá? Estão perguntando ali, Pedro, o que que é o por que isso aí é verdade, cara? O 160 ele é 2 x 80, né? Então, ou seja, você não tem aqui eh você não tem aqui nenhuma nenhuma. Tô pensando aqui no negócio. Tem uma diferença dele por 80 assim. É, tem uma diferença dele para 80. Pô, eu acabei de pensar aqui, tem um
divisor que ele vai ter, que não vai ter, esquece essa regra, né? Eh, eu viajei falando isso, é porque ele ele pode ser dividido 160, ele pode ser dividido, por exemplo, pelo 32. Então, se ele pode ser dividido pelo 32, né, ele ele justamente não tem não tem essa regra, não. Tá bom? Então, olha só, vamos ter que fazer de novo mesmo com atenção para não perder nada, tá bom? Então, aqui, ó, 160 dá para dividir por um, claro, qualquer número dá, dá para dividir por dois, dá para dividir por três, não dá. Dá para
dividir por quatro? Sim, por quatro dá. E também dá para dividir por oito, com certeza. Tá, dá para dividir ele por ã 10? Sim, por 10 dá, por9 não dá, tá? Ã, pulei o cinco de novo, né? eu tô com muito sono, tô errando tudo. Então, olha só, botar aqui o cinco. Dá para dividir por 8? Dá para dividir por 10. Vamos lá. Dá para dividir por 12? Não, por 12 não, né? O 12 x 12 dá 144, depois vai dar 156, não vai chegar nele. Dá para dividir por 15? Não. Dá para dividir por
16? Sim. Por 16 dá, né? Dá exatamente 10. Eh, dá para dividir ele por 20? Dá, dá para dividir por 20. Dá para dividir por 24? Não, não vai dar para dividir por 24. 24 já daria 5 x 24 dá 120. Depois daria é, não dá. Não dá para dividir por 25? Não, não dá. Não, exato, né? O 25 dá 125, depois dá 150, depois dá 175. Por 30 não vai dar, por 32 vai dar. 160 ele é divisível por 32, né? E vai dar exatamente cinco, tá? Dá para dividir ele por 40? Dá. Dá
para dividir o 160 por 50? Não vai dar. 45 não vai dar. Dá para dividir ele por Agora a gente já entra na na reta final. Agora dá para dividir por 80 e também dá para dividir pelo próprio 160. Beleza? Show. É isso aí. Então a gente tem aqui todos os divisores do do número, tá? Agora imagina isso aqui cai realmente, ó. Você tem uma noção e só aparece na prova esse tipo de desafio, né, em que você precisa descobrir esse tipo de coisa. Não aparece assim, ó, quant nunca aparece quantos divisores t, só aparece
dentro de uma questão. E eu tô te falando, até aluno de autodesempenho se confunde com isso, né? Então, até eu me confundo com isso. Imagina, né, se você não treina isso aqui, tá bom? Eh, lá na hora é é muito fácil você pular um divisor, cara. É extremamente fácil você pular um aqui, tá bom? Perguntaram se não dá pro 100. Não, 160 dividido por 100 vai dar 1,6, tá bom? Então, assim, o 160 é o que eu falei, ele não é um número primo, tá? E aí, né? Eh, como que você faz para você escrever
ele com números primos, né? Ele é a mesma coisa que o 80. Lembra que o era 2 x 2 x 2 x 2 x 5? A única diferença é que tem mais um do aqui, né? Então ele tem que dobrar de novo. Mas ele tá escrito aqui somente com números primos. Beleza? O 320 agora, nossa, vamos nessa. Bora. Vamos lá, então. Bora. Eh, 320. 1 2 Eu tô meio meio lerdo da cabeça. 4 5 Dá para dividir o 320 por 5? Claro que dá, né? Você dobra 640, dá 64. Dá para dividir por 6? Por
se não dá. É, por seis não dá, porque para ser divisível por seis tem que ser divisível por dois e por três. E para ser divisível por dois ele é par. Tudo bem. Por três teria que somar isso aqui, dar um número divisível por três. Não dá. Beleza? Eh, vamos lá, então. Eh, dá para dividir por 7, 8, dá para dividir por 8, claro, né? Até porque 32 é divisível por 8. Dá para dividir por E aí se for ali 320 também vai ser. Dá para dividir por 10, dá para dividir por 16, é claro,
né? Dá para dividi-lo aqui por 20. É claro que dá, né? 100, 300. Isso aí dá para dividir por 20. Dá para dividir por 25? Não dá para dividir aqui por 30. Não dá para dividir por 32. Claro que dá, né? Dá para dividir por 32. Claramente dá para dividir por pelo dobro de 32. Certamente dá, né? Por 64, claro, né? 64 x 5, né? 5 x 64, 5 x 60, 300. 5 x 4 dá isso. Tá bom. Eh, dá para dividir por 100 e não, agora do 64. Deixa eu investigar aqui. Ã, eu pulei
aqui o 40, acabei de perceber. Eu olhei ele para cima, lembrei que eu pulei o 40, né? Dá para dividir antes pelo 40, né? E agora sim a gente pode dizer que dá para dividir pelo 64. Tá? Agora depois disso, cara, depois do do Não, pô, 50 não. Falaram que eu pulei o 50. Aí é sacanagem, pô. 50 não é divisor, pô. Tá maluco. 320 por 50 não dá. É, não dá, pô. Dá 6,4. Não dá. Exato. Tá. Agora vem aqui o 80, né? que dá 320 por 80 dá 4. Eh, agora tem que ser
o resultado que dê 320 por é, tem que ser o resultado que dê que dê dois agora, né? Porque não vai ter nenhum resultado que vai dar três, então tem que ser um resultado que dê dois, então tem que ser já próprio 160, depois 320. Esses são os divisores, tá bom? E é claro que o 320 ele pode ser escrito como 2 x 2 x 2 x 2 x 2 2 4 8 16 32 assim, tá bom? Vezes 264. Isso aqui também é o 320 escrito apenas com fatores primos, tá bom? A gente pode juntar
ele como sendo 2 a 6 x 5 a 1. Beleza? Isso vai ser importante pros próximos exercícios, tá bom? Beleza. Vamos lá, então. 144. Quais são os divisores do 144? Dá pra gente dividir o 144 com exatidão pelo 2. É pelo 1, óbvio, né? Não pode esquecer, começa sempre pelo 1. Pelo 2 dá para dividir por 3. Ó, 4 + 4 dá 8 + 1 dá 9, né? Então é divisível por 3 também, com certeza. Tá, dá para dividir o 144 pelo pelo 4? Sim, dá 36. Exatamente, né? Dá para dividir o 144 por 6?
Sim, eu já penso assim, olha, o se ele pode formar o 60, depois pode formar o 120 e do 120 pro 144 vai ter mais 24. Esse 24 é divisível por se, entendeu? Então você consegue formar o 144 indo de seis em seis, entendeu? Se aí vai pro 60, aí vai pro 120. Aí do 120 vai até o 144 com mais 24, tá bom? Dá para dividir o 144 aqui por 8? Ã, tem que dar, porque com oito você consegue formar o 80, depois falta mais 64, você também forma o 64, entendeu? Você conseguiu visualizar
isso? É só você ver se indo de oito em oito você consegue chegar no 144. Então do oito tu já vai pro 80, né? Porque já tem 10 números oito. Aí agora do 80 até o 144 falta 64. Também vai ter aí mais oito. A gente consegue saber até que dá 18, né? Porque 8 até 80 tem 108. Agora com mais 64 tem 8 dentro do 64. Então tem 18 números oito aí, tá bom? Então dá para dividir por oito também. Dá para dividir ele por 12, claro, né? Tô mostando algum. Pera aí. Por nove.
Por nove também dá para dividir, né? Por nove. Porque o o você para você saber se o número é divisível por você soma os algarismos dele e aí você vê se ele é divisível por 9, assim como por três, né? Você som por três. Para tu saber se é por 9, tu soma e vê se é por nove. Então 4 + 4 + 1 dá 9. 9 é divisível por 9. Agora assim vem o 12, cara, por 15 não vai ser. Tá bom? Ã, deixa eu ver aqui. Por 16 dá, né? Porque 10 x 16
seria 160. Se tu retirar um 16 vai pro 144, né? Então 9 x 16 dá justamente isso. E agora por mais quem? Por 20 não dá. E por 11 não. Por 11 1213. Não, 121, 132. Não, não, não. Por 11 daria 143 por 18. Deixa eu ver se por 18 dá. Deixa eu verificar aqui. 18 36 72 dá. Por 18 dá, né? Por 18 dá. Porque 18 36 aí dobra o 36, só pra gente já acelerar, né? Vira 72. Aí dobra o 72, vira o 144. Tá bom? Eh, agora dá para fazer por 20, dá
para fazer por 22? Não dá. Dá para fazer por 24, talvez dê para fazer por 24, né? Então aqui 24 dá para tu multiplicar o 24 por 5. Quando você multiplica o 24 por 5, dá 120. Aí tu bota mais um 24, você chega no 144. Tá bom? Então também dá para dividir ele por 24 certinho. A gente vai começando a a gente vai começando a falar ali, Pedro, ensina os critérios de divisibilidade. Tá na apostila, velho. Entendeu? Botei na apostila aqui, tá? Tá até antes, entendeu? Só não repetir aqui porque já tem uma aula
bem longa que eu falo sobre isso que tá aqui no módulo, tá? Eh, agora do 24, cara, o próximo divisor aqui vai ser o 36. 36, tá? Agora, o próximo divisor aqui, o 144 pelo 36 já dá 4. Então a próxima resposta teria que ser uma que dá três, né? Mas ã, é, o 144 é divisível por 3, então ele tem que ser dividido por quem? Para ele dar três? Tem que ser dividido pelo 48. 144 dá para dividir por 48, tá bom? E vai dar exatamente 3, tá? Agora o 144 por alguém que dê
dois, né? Porque aqui o 144 é divisível pelo 36 e dá 4 e pelo 48 dá 3. Agora tem que ser divisível por alguém que gere o número dois, né? Só pode ser o próprio 72 e agora o próprio 144. Tá bom? Esses são todos os divisores, galera. É muito, muito, muito raro que isso aqui apareça, que isso aqui caia desse jeito com essa extensão toda, mas se cair, né, é bom que esteja preparado, porque muitas vezes aparece coisa assim, tá? Quero dizer, coisas estranhas aparecem na prova, tá bom? 81, vamos lá. O 81 é
divisível por quem? por um, por três, por se ele não é, tá? Por s ele também não é. Ele é divisível por 9. Ele é divisível pelo pelo 12. Não, agora ele só vai ser divisível mesmo pelo 27, né? É o próximo número. Eh, 69. Tô só investigando aqui se pelo 13 ele é. Eu acho que pelo 13 ele não é. Não, 13 não, 39. Aí o dobro de 39 é 78. Aí 78 não é não. Não é divisível pelo 13, não. E pelo 81. Acabou. Esses são os divisores dele, graças a Deus. Tá bom.
Agora o 90 pra gente dar um trabalhinho mais, né? O 90 é divisível por 1, é divisível por 2, é divisível por 3, é divisível por 5. Dá para você dividir 90 por 5, que vai dar um resultado certinho, vai dar o resultado de 18, né? 90 dá para dividir por 6 certinho também. O 90 dá pra gente dividir por por 8? Não dá. Exato. Mas porve dá. Dá para dividir o 90 por por 12? Não. Não dá. Dá para dividir o 90 por 10, claro, né? Vai dar certinho. Tinha esquecido aqui do 10. Dá
para dividir o 90 por, eu tô mostrando. Dá para dividir por 10. Eu tava quase esquecendo. Dá para dividir o 90 por 12, não dá. Então agora é por 15, né? O próximo com certeza é o 15, né? que dá seis a divisão. Agora a gente procuraria uma divisão que desse cinco, mas aí seria por 18, entendeu? Já tô olhando os resultados porque 90/ 10 deu 9. Aí a próxima possível é 90/ 15. A gente nem bota o resultado, mas a gente sabe que 90 por 15 vai dar 6. A próxima é uma possibilidade que
dê cinco, né? 90 dividido por alguém que dê cinco. Tem que ser pelo 18. A próxima agora é uma que dê quatro, tá? O 90 dividido por quem daria quatro? Não tem 90 dividido, não tem um divisor que vai resultar nesse quatro, entendeu? pro pro 90 ser dividido por alguém que dê 4, ele teria que tá sendo dividido ali pelo 22,5, né? Eh, agora o 90 dividido por alguém que dê 3 tem, né? O 90 dividido, no caso, pelo 30 vai dar 3 e aí 90/ 45 vai dar 2. 90 dividido por 90 vai dar
1. Beleza? É ótimo, acabou aqui, tá bom? Eh, aqui, ó, reescreva, vamos fazer só mais umazinha. Reescreva em fatores primos seguintes números e aglomerando as potências quando for possível, tá? Eh, com os expoentes das potências. Então vamos colocar aqui só pra gente fechar isso aqui. A gente quer reescrever os números em fatores primos, tá bom? Então vamos vamos escrever aqui. Só tem um jeito de fazer, tá bom? Não tem dois jeitos de fazer isso aqui. Ah, pode fazer assim ou assim, não. Tem só um jeito de fazer. O número ele é feito por uma codificação
de fatores primos única, tá? Não tem dois jeitos de fazer. Se tu dissesse que tem dois jeitos de fazer, é porque algum número dali não é primo, tá? Então ove, por exemplo, ove ele só pode ser escrito como 3² em fatores primos. Ah, Pedro, não é 3 x 3, é a mesma coisa, só que eu falei para aglomerar as potências, tá? E botar o expoente delas aqui, tá bom? O 16 ele pode ser escrito apenas como sendo 2 elevado a qu Pedro, mas o 16 não pode ser o 2 x 8? Você não tá escrevendo
em fatores primos porque o 8 não é um fator primo, entendeu? Aí estão falando ali, qual que você tá dizendo que é a outra forma de fazer? Eu falei que só tem uma forma. A única forma de escrever em fator prima é essa daqui. 2 elevado qu, tá? Que é o 2 x 2 x 2 x 2. Não tem outra forma de você escrever isso aqui em fatores primos. Aí ele falou assim, ó. 4², mas 4 é primo, meu anjo, meu lindo. O quatro não é primo, concorda? Sacou? É isso que eu tô te falando.
O quatro ele pode ser escrito em si como 2 elevado a 2 e isso aqui tá elevado a 2 já, entendeu? Aí fica 2 elevado qu, beleza? Esse é o problema. Então eu falei assim, escrevendo como fator primo, só tem um jeito de fazer, tá? O 25 ele pode ser escrito como sendo o 5 quad, tá bom? Em fatores primos. Eh, o 49 ele pode ser escrito como 7 quad, tá? Em fator primo já, não tem outra forma. O 120, ai Pedro, 120 ele pode ser escrito como 3, o 3 x 40, mas aqui não
tá escrito em fatores primos. O 40 não é primá, então vou escrever o 40 aqui como sendo eh o 2 x 20, mas não tá em fator primo porque o 20 não é primo. Então vou escrever o 20 aqui como sendo também um 2 x 10. Não tá em fator primo porque o 10 não é primo. Então o 10 vai ser o 2 x 5. Tá bom? Agora tá em fator primo, só tem número primo aqui. Então essa é a única forma de escrever ele como primo. Não tem outra forma de você escrever uma codificação
de números primos para ele. Decompõe fator primo é uma coisa só. O que você pode fazer agora é aglomerar. Tá vendo aqui? Tem três números dois, né? Então você vai botar o quê? Os três aqui organizadinhos, ó. 2 elevado 3 x 3 x 5. Agora sim, essa é a resposta. E como eu falei para indicar as potências é para botar até a mesma potência de um aqui, tá? Para deixar bem certinho, tá? Confia que isso aqui vai ser importante pros próximos exercícios. Eu não botei aqui à toa, tá? Ai, Pedro, como é que eu o
170 eu não consigo visualizar? Você sabe qual macete para você sempre acertar? Começa a quebrar por algum número primo que tu consiga. Por exemplo, 170 no A. Não sei qual é a codificação dele em fator primo, tá bom? Mas você consegue dividir ele por dois, concorda? Porque ele é par. Então tu vai escrever aqui, ó, 2 x 85. Pronto, você já tá acertando aqui. Agora, o que que eu faço? Pego o 85 e divide por dois. Ah, mas não dá para dividir. É, então não divide por três. Ah, mas não dá para dividir. Então divide
por cinco. Cinco é o número primo e dá para tu dividir. Então 85 di por 5 de cabeça. 85 di por 5 você dobra e divide por 10. Então você dobra, ele vai virar o 170, divid por 10 dá o 17. Então ou seja, 85/ 5 nada mais é do que o 5 x 17. Concorda comigo? 5 x 17. Lembra que eu tinha 85? Eu peguei o 85 di por 5. Aí eu consegui escrever ele. Quanto que dá isso? 17. Ó, pera aí, deixa eu só mostrar aqui que eu acho que tem gente que não
visualizou. tinha um 85. Eu falei assim: "Cara, eu quero dividir ele por algum número primo. Ah, vou dividir pelo cinco. Quanto que dá isso? Dá 17. Então, para eu escrever o 85 nesse formato, eu passo o cinco para cá. Entendeu? O 85 nada mais. Eu consegui descobrir que o 85 é o 17 x 5, entendeu? Você multiplica 5 x 17 que você vai ver que dá 5 x 10 50. 5 x 7 35 volta a ser 85. Tá bom, Pedro? Eu poderia ter começado aqui escrevendo como 17 x 10. Claro. Aí agora você, o 17
ele já é primo. O 17 é primo. Só dá para dividir o 17 por 1 e pelo 17. É isso mesmo. Pode começar separando o 10 também. Agora o 10 você chega aqui, tu separa também em 2 x 5. Tu vai achar 17 x 2 x 5. E eu também achei a mesma coisa. 17 x 2 x 5. Essa é a resposta. O 170 ele só pode ser codificado em número primo assim, ó. 2 a 1 x 5 a 1 x 17 a 1. Não tem outro jeito de escrever como número primo. Tá bom? Beleza.
OK. Hã, rapidinho, só um instante. Pronto. O 290. Ah, Pedro, não sei o que fazer, cara. Começa dividindo ele por 10 logo, né? Vai dar para dividir por dois, claro, mas você pode. Não tem como errar isso aqui, tá? Então, vamos lá. 29 x 10 tá em número primo. O 29 é primo já. Não tem como você dividir o 29 por mais ninguém. Ah, só dá para dividir pelo 1 e pelo 29. E o 10? O 10 não é primo. Então, escreve o 10 como 2 x 5. Aí agora já é primo, tá certo? Essa
aqui é a resposta. já tá fatorado. Isso é fator um número e número primo. Que que é fator? Fator são as coisas que se multiplicam. Você tá escrevendo 290 como fatores multiplicativos, tá? 34. Não, não tem outro jeito, né? O jeito é esse. O outro jeito é mais trabalhoso. É você começar fazendo assim, 2 x 14, mas o 145 ele pode ser dividido por 5. Aí se tu dividir ele por 5, ele vai dar 29 x 5. Aí vai dar a mesma resposta. 2 x 29 x 5, tá? 34 di por 2 x 17 pronto,
tá faturado em número primo. 22 di por 2, x, pronto, tá faturado. Em número primo, 2 é 1 x 11 é 1. O 21, sei lá, divide por 3. Então, como é que fica? O 21 pode ser escrito como 3 x 7, tá aí número primo. 3 a 1 x 7 a 1. 420. Quer começar escrevendo 42 x 10? Perfeito, mas nenhum dos dois é primos. Dá para tu dividir o 42 por 2 por um monte de gente. Então agora vamos deixar eles, né? Vamos quebrando mais. Então lembra que tu escreveu 42 x 10? O
42 você pode escrever como 2 x 21 e aí o 10 você pode escrever como 2 x 5, tá? Aqui já é primo, aqui já é primo, mas o 21 não é primo, porque o 21 ele ainda pode ser divisível tanto pelo 1 quanto pelo 21, mas também pelo 3, também pelo 7. Então o 21 vamos escrever ele como sendo 3 x 7. Agora todo mundo que tá aqui é primo, todo mundo. Agora vamos aglomerar as potências. Tem 2 elevado 2 x 3 elevado a 1. E aqui é o 2 elevado 2, né? V x
7 elevado 1. Tá fatorado em número primo. 76. Pô, vou começar escrevendo como 2 x 38. Perfeito. Quebra o 38 agora em 2 x 19. O 38 é isso. É 2 x 19. Acabou. Tá em número primo. Só falta aglomerar as potências. 2 elevado 2 x 19 elevado 1. 19 é primo. 2 também é. Esse aqui é o 76 escrito em formato de número primo. Entendeu? Mais uma questão aqui concluída, tá bom? Parabéns aí a todos que assistiram. Até a próxima. Um beijão. Sejam bem-vindos novamente a mais uma aula da plataforma SAD. E agora a
gente vai focar aqui nos números positivos e negativos, tá bom, galera? Eh, tá na apostila, tá bom? Tá detalhado lá na apostila, tá bonito, né? A gente, eu expliquei bem claramente lá sobre os números positivos e negativos. E também tá nas aulas aqui do ciclo, né, nas aulas do alfabetização e matemática, tem explicando sobre isso, tá bom? Então, eh, é o número negativo, assim, vamos lá. A nível de soma e de subtração, você sempre tem que pensar neles como saldo positivo e saldo negativo. Só isso, tá? Isso sempre tem que ser assim, saldo positivo e
saldo negativo. Então, tudo que for positivo que for aparecendo, você vai somando no teu caixa positivo. E tudo que for negativo é uma dívida, tá? Então, por exemplo, vou te dar de presente aqui um número, tá? Eu vou te dar de presente para você o número -9. Soma aí -9 na tua conta, ó. Tu vai ganhar agora um presente, né? Tu vai ganhar o quê? O número -9. Você no final você vai ter perdido, né? Você ganhou um número negativo, você botou um número negativo ali, cois você perdeu, tá? Você ficou com -9 agora, tá?
Então essa é a mentalidade, tá? Tanto nas aulas teóricas daqui do capítulo do ciclo de nivelamento intelectual, né? Quanto na apostila, tá? Então o que falta aqui agora é fazer. Agora, quando for multiplicar e dividir, você só tem que saber o seguinte: multiplicar por um número negativo sempre inverte o sinal de quem já tá lá. Só isso. O número negativo ele ele é um inversor de polaridade. Quando você bota um número negativo, você multiplicando ou dividindo, você inverte quem tá lá, tá bom? Então, por exemplo, aqui, ó, eu tenho -8 x 10. Ué, esse 10
não tá com nenhum sinal, então ele é positivo. Então, quanto seria só? Você sempre vai multiplicar tanto os sinais quanto os números. Só que, pô, só tendo aqui um negativo, seria um negativo vezes um positivo. Aqui não muda nada, é o negativo mesmo que vai atuar, tá bom? Aliás, se você quiser pensar nesse positivo como referência, o negativo vai fazer o que com ele? Vai inverter ele. O negativo vai fazer com que ele vire um menos, tá? Então, eh, por isso que a gente diz assim, ó, negativo vezes positivo dá negativo. Mas na verdade, né,
eu gostaria que você pensasse que o negativo ele inverte o sinal do alvo dele, tá bom? Então, quando você multiplica aqui negativo com positivo dá negativo e o 8 x 10 dá o quê? 80. Então, dá -80. Tá bom? Quanto é -4 x -4? Ô, o negativo inverte o negativo, então vai fazer ficar positivo, tá, Pedro? Qual negativo inverteu? Qual? Tanto faz, pô. Se você quiser fazer aqui esse negativo, inverte esse, tanto faz. Um negativo inverteu o outro, né? Então ele fez o outro ficar positivo, tá bom? Então por isso que menos com menos dá
mais. Beleza? Não, a apostila teórica tá disponível sim. Tá disponível, tá lá no capítulo, inclusive. Vai lá no ciclo de nivelamento intelectual, tem materiais, tem apostila lá, tá bom? Então aqui, ó, menos com menos dá mais. 4 x 4 dá 16. Então isso aqui dá 16 positivo, tá? Quanto é agora aqui começa a ficar mais importante, né? Menos vezes menos, primeira coisa sinais, né? Menos xzes menos x vezes menos, depois 2 x 2 x 2. Já sei que vai dar 8, né? Isso aqui é moleza para mim. Agora o sinal, né? Menos vezes menos, um
menos inverte o outro, fica positivo, né? Aí agora tu tem um positivo vezes um menos, vai ficar o quê? Negativo de novo. Tá bom? Beleza. É isso então, né? Menos vezes menos dá mais. E agora esse mais vezes o menos fica o menos. Beleza? Ã, - 40 x + 40. Aqui só tem o menos, né? Então vai ficar menos, porque menos vezes mais deixaria ele como sendo menos. Agora 40 x 40. Como é que a gente faz isso? A gente pode fazer primeiro 4 x 4, concorda? Que dá 16. Agora, além disso, ainda tem um
zero e um zero aqui, né? Tem como se fosse um 10 e um 10 ali. Então, bota ali mais dois zeros, tá bom? É como se fosse, ó, quando você vê 40 x 40, eu quero que você pense assim, ó. É como se fosse isso aqui, ó. O 40 não é um 4 x 10. Então aqui, ó, 4 x 10 x 4 x 10. 4 x 4 16. Aí xes 10 + 1 0 x 10 outro zero. Tá bom? Por isso que a gente só pega e bota os dois zeros ali no final, tá bem?
- 0,3 x 10. Primeira coisa, o sinal, né? Menos vezes mais tem que dar menos. Agora 03 x 10, né? Ou 10 x 3 dá o quê? 3. Tá beleza? O parêntese ele não muda nada não, cara. O parêntese ele só deixa mais organizado, entendeu? Então que eu botar aqui um parêntese tranquilo, entendeu? Tá vendo aqui assim -4 x -4? Ele poderia dar assim, ó, -4 pontinho e aqui um -4, mesma coisa. Vai multiplicar o menos com menos, vai dar o quê? Mais e o 4 x 4 vai dar 16. Tá bom assim? Deu para
visualizar aí? Sim. Vamos lá, então. Então, aqui, ó, 10 x 0,3 dá 3. E aí o menos ali ainda fica menos -3, tá bom? E aqui do nada tem uma operação aqui que envolve, né? Não tem multiplicações nem divisões aqui. Então, como é que fica isso aqui? Eu tenho sempre que ter a mentalidade de pensar em saldo positivo e dívida, né? Eu pensar em tenho e devo, né? Coisas que eu tenho e coisas que eu devo. Beleza? Então, aqui eu tô devendo 100. Se você quiser, é, perguntaram ali, se fosse assim, Pedro, -4 x -4,
aí é positivo, é a mesma coisa, né? Ah, tá, entendi. Ela perguntou assim, ó. Não, e se fosse o -4 vezes um menos e aí o -4? É, primeiro teria isso aqui, quer dizer que tem um aqui, né? Esse menos aqui sozinho só pode ter um um aqui, né? Então, primeiro menos com menos dá mais. Aí agora esse menos contra esse mais vai fazer ele voltar a ser menos, né? Então vai ficar -1. Beleza? Tá. Não, não, não. Eh, falaram assim, mas Pedro, e antes de um parêntese que não tem sinal nenhum, não teria um
sinal positivo. Mas mesmo que tivesse o sinal positivo, não muda nada. Sinal positivo numa multiplicação não altera nada. O sinal positivo, ele não muda nada. Sinal positivo é irrelevante, é o sinal negativo que importa. O sinal negativo ele sempre inverte o que tá acontecendo. O positivo não altera o que tá acontecendo. Tá bom? Todo mundo tá aí, né? Então, olha só. Aqui você não tá vendo nenhuma multiplicação, então é só uma questão de você acumular tuas dívidas e acumular o teu saldo positivo. Se quiser pode fazer primeiro negativo, pode. Ó, -1 com -40 tem -10,
com -22 tem -12. Nesse -12 tu chega com 80 positivo. Então tu tá devendo 182, tu só paga 80, tu vai continuar devendo - 102. Visualizou? Não faz diferença nenhuma. Pergun estão perguntando Pedro. Se for assim, ó, -4 x -4, me responde você. Que que tá acontecendo aqui? Que que tá acontecendo aqui? Visualiza só. -4 x -4, ó. Menos xes menos aqui vai dar mais. 4 x 4 vai dar 16. Beleza? Então se preocupa sempre que usou parênteses é só para para organizar, tá bom? Então falando aí que eu confundindo essa daqui, ó. Deixa eu
ver aqui. -1 com -40 com -22 é -12, né? Eu falei -12. Eu errei na parte que eu acumulei as partes negativas, tá? Então, eh, o -1 e aí eu tenho -40, eu tenho -10 já. Agora eu tô com -22 ainda, então eu tô com -162. E aí, nesse men 162 eu tenho 80 para pagar. E aí eu fico, eu tô devendo 162, mas eu pago 80, eu vou continuar devendo, mas eu vou ficar devendo menos 82, tá bom? Então assim, eh, claro que tem um macete assim, né, que as pessoas falam que, olha, quando
a gente tá fazendo uma uma operação, eh, quando a gente tá fazendo aqui uma operação assim de mais com menos, vamos supor assim, ó, tu tem mais 100, men, prevalece o sinal do maior, do maior em módulo, né? Então, o 100 é o maior. É, concordo. Prevalece o sinal do maior, mas eu gostaria que você tivesse a mentalidade de pensar assim: "Cara, eu tenho 100 e eu tô devendo 82, então eu vou conseguir pagar os 82 e vou ficar ainda com 18 positivo, tá bom?" Então aqui 18, tá? Beleza? Vamos lá. -50/ 5, galera. Da
mesma forma, -50/ 5, se você tem numa divisão, numa fração, tá bom? Beleza? Se você tem aqui uma uma fração e você e você tem um sinal de negativo aqui nela, a resposta tem que ser negativa. Lembra que eu te falei? Eu te disse assim: "Olha, um sinal negativo, ele vai ficar negativo, né? É como se eu tivesse aqui embaixo um positivo. Eu tenho um positivo. Como é que é negativo com positivo? Fica negativo mesmo. Tá lembrado disso? E se eu falar para você assim: "E se eu tivesse, na verdade, um sinal de negativo embaixo
dessa fração? mesma coisa, a resposta fica negativa, tá bom? E agora, e se eu tivesse um sinal de negativo em cima e embaixo? Aí sim, negativo com negativo vai dar um positivo na resposta, tá bom? Só para você ter aí essa essa clareza, visualizar isso, tá bom? É a mesma coisa que na multiplicação. Mesma mesma coisa que na multiplicação, tá? Da mesma forma, beleza? Eh, então, por que que 10 x -5 dá -50? Cadê, né? Tem essa conta aqui, cara. Porque 10 x -5, eu tenho um 10 ali positivo. Ah, tá. Tu tá falando, né?
Tu não tá perguntando. Beleza. Isso aí falou aqui. Tá bom. Então, olha só. Vamos lá. -50 di por 5. Só de eu ter aqui um sinal de menos, eu já sei que vai ser menos. Agora 50 por 5 dá 10. - 10. Pronto. Tá. Agora - 100 dividido por -4. Concorda que aqui é como se eu tenho aqui um - 100, aqui eu tenho -4. Aí sim é um negativo com negativo, né? Um negativo inverte o outro, viraria um positivo, tá bom? E aí 100 div por 4 daria 25. Então é 25 positivo. Essa é
a resposta, tá bom? Eh, 80 di por -20. Aqui eu tenho um 80 di por um -20, né? Então aqui sim eu tenho justamente ã um um sinal negativo apenas. Então a resposta vai ter que ser negativa. Agora 80 dividido por 20, né? A mesma coisa que 8 por por 2. Então eu tenho aqui -4 como sendo a minha resposta. Beleza? Agora -1/ -8. Isso aqui vai dar positivo, tá? Não, esse negócio de dívida e saldo não é para divisão e multiplicação não, cara. É só para soma e subtração. É só quando você não tem
multiplicação e divisão, tá bom? Então aqui, ó, menos com menos tem que dar mais, concorda? Porque -1/ -8, ó, é multiplicado aqui, né? Eu tô achando que é dividido, mas enfim, sendo multiplicado também, né? O o tanto na multiplicação quanto na divisão dá positivo, tá bom? Então, o menos vezes o menos dá positivo. E quanto é 8 x 12? Você lembra que multiplicar por 8 é dobrar, dobrar e dobrar? Então, pega o 12, dobra 24, dobra 48, dobra 96. Ou seja, dá 96 aqui positivo. Beleza? Ótimo. Então, mais uma vez aí a gente finalizou o
esse esse exercício. Agora a gente vai pra próxima parte de múltiplos e divisores, tá bom? Um beijo. Vamos pra próxima. Pronto, finalmente agora você chegou em potenciação. Esse é um assunto que muita gente pensa que sabe, mas na verdade muita gente tem deficiência em potenciação. Então, nessa aula aqui agora, tu vai entender essa impotenciação de um jeito absurdo, tá bom? Já vai preparar para entender radiciação também. Isso aqui te limita muito. Se tu não sabe potenciação de verdade, tu não sabe nada de logaritmo, de função exponencial, de equação exponencial, não consegue fazer um monte de
coisa de de equação de segundo grau, não consegue fazer um monte de coisa de física, então é uma tragédia não saber potenciação nessa aula que eu vou resolver. Não repara porque eu tava um pouco rouco na época que eu gravei esse vídeo, mas né, espero que dê para você acompanhar. A galera sempre consegue acompanhar. Então é só para te explicar mesmo, né, que a minha voz tá um pouco estranha, mas daqui a pouco isso melhora. Então vamos nessa, vamos para dentro. Tá mandando muito bem. Tô gostando de Sejam todos muito bem-vindos a mais uma aula
da plataforma SAD. Nessa aula aqui a gente vai ter a teoria completa, sólida e imbatível de potenciação para que você realmente fique bem de vez dessa matéria sem precisar de uma decoreba excessiva, né? Sem precisar ficar e com muita ah tais propriedades, aquelas. A gente vai aprender tudo a partir de uma única propriedade, beleza? Quando a gente fala de potenciação, a gente sempre tá falando de alguma base elevada a algum expoente. Isso aqui tudo a gente chama de potência. Isso é uma potência, tá? Então isso aqui é a base da potência e esse é o
expoente da potência. Então, por exemplo, se eu tiver assim, olha, 5 elevado 2, é isso, 5 elevado 2 é uma potência. Essa aqui é a base dessa potência, beleza? Então aqui a base dela é cinco. Eu quero que eu quero que você pegue esse vocabulário, porque isso faz diferença. Então assim, ó, você vai dizer: "Olha isso aqui é uma potência de base cinco. Potência de base cinco. E essa aqui, por exemplo, é outra potência de base C. E essa aqui, por exemplo, é outra potência de base COC, tá bom? Essa é uma potência expoente dois.
Essa é uma potência de expoente 3 e essa é uma potência expoente 4. Como que a gente fala isso aqui? A gente diz assim: "Olha, aqui temos o 5 elevado 2, aqui temos o 5 elevado 3 e aqui temos o 5 elevado 4.", beleza? Ã, só que esse 5 elevado 2 a gente também pode chamar de 5², beleza? E esse 5 elevado 3 a gente também pode chamar de 5³. E esse 5 elevado 4 não tem um nome específico para ele, a gente só chama de 5 elevado 4. Só que a partir daqui a gente
pode também chamar sempre de 5 à qu potência, né? 5 a terceira potência, 5 a segunda potência. Mas isso é um número, isso é uma nomenclatura que a gente usa menos. Geralmente a gente fala 5 elevado 2, 5 el 3, 5 elevado 4 ou 5², 5³ ou 5 e aí depois 5 a5, 5 a6, 5, depois 5 elevado 12, assim vai. O que que significa uma potência, né? É, é muito importante que você internalize isso. É óbvio que é uma coisa simples, mas não é 5 x 2, tá bom? 5 elevado 2. Esse número aqui,
ele sempre indica o número de vezes pelo qual a base deve ser multiplicada por ela própria. Então 5 elevado 2, na verdade significa 5 vezes ele mesmo duas vezes, que dá 25. 5 elevado 3, na verdade significa 5 vezes ele mesmo três vezes, que dá 5 x 5= 25 e x 5 dá 125. E 5 elevado 4 é o 5 vezes ele mesmo quatro vezes. Então o cinco se repete multiplicando quatro vezes e até aqui dava 125 e agora passa a dar 625. Beleza? Então isso aqui é o básico de potenciação, tá bom? Quando a
gente pensa aqui nas potências de base dois, com certeza é bem importante, né? Se você pensar assim, 2 elevado 1, 2 elevado 2, 2 el 3, 2 elevado 4, 2 el 5, 2 el 6, 2 el 7, 2 el 8, 2 el 9 e 2 el 10. Quando a gente tem 2 elevado 1, é o 2 vezes ele próprio uma vez. Isso dá 2. 2 elevado 2 é o 2 vezes ele mesmo duas vezes. Então 2 x 2 dá 4. Ele 3 é o 2 vezes ele mesmo três vezes. Então isso aqui dá 8. 2
x 2 x 2 dá 8 e 2 x 2 x 2 x 2 dá 16. E agora nas próximas potências é importante que você só pense assim em adicionar mais um dois na multiplicação. Então se o 2 à qu dava 16, quando você bota mais um do ele vira 32. Com mais um do ele vira 64. Com mais 1 2 ele vira 128. 2 é 256. Vai só dobrando cada vez mais, né? 2 a 9 é 512 e 2 elevado 10 é 1024. E assim vai, tá? Ã, essas são aqui as potências de base dois,
né? É bem importante conhecer elas, tá? Então, a primeira eh regra de potência, que é uma regra que você precisa aceitar meio que na decoreba mesmo, na marra, é que qualquer número elevado a zero dá um. Qualquer número, tá? Então, por exemplo, quanto é 2 elevado a 0? Isso é 1. E quanto é 3 elevado a 0? É 1. Quanto é 7 elevado 0? É sempre um. Tá? Isso é uma coisa que eu realmente gostaria que vocês só decorassem, tá bom? Só decorassem, né? Qualquer número elevado a zero dá 1. Então 160 elevado a 0
dá o quê? Um. Agora qualquer número elevado a 1, ele dá ele próprio. Porque se eu tiver 2 elevado a 1, é o 2 vezes ele próprio uma vez. Então é dois, né? Se eu tiver 3 elevado a 1, é o trê vezes ele próprio uma vez. Então isso dá três. Se eu tiver 7 elevado a 1, é o 7 vezes ele mesmo uma vez. Isso dá sete. Eh, entra se 0 elevado a zero. Não, não, não dá para elevar o zero a nada. O zero nunca pode ser a base, tá bom? O zero nunca
vai ser a base, beleza? Não existe zero elevado a zero, tá bom? É, o zero não pode ser uma base, tá? Porque você vai colocar o zero aqui, vai colocar qualquer coisa aqui, é o zero vezes ele mesmo. Não tem como você fazer zero vezes nada, né? Zero vezes ele mesmo vai dar zero, não tem como, independente do que aconteça, tá? Então 0 elevado a zero não existe, não tem esse essa parada, isso aí não não acontece, tá? OK? Então aqui já tem o primeiro nível básico de potenciação, tá bom? A gente já fez aí,
a gente tem treinamentos aí gravados, né, em que eu resolvo várias potências básicas. Então eu não vou entrar nisso agora, porque a gente já fez isso. Eu não vou eh começar a resolver potências básicas que a gente já sabe isso. Ah, 7 elevado 3 é 7 x 7 49 x 7 de novo dá 343. Beleza? Show. O que a gente vai fazer agora é pegar as propriedades um pouco mais avançadas, tá? Então vou começar a pegar os casos um pouco mais avançados. O primeiro caso que a gente pode dizer que ele é um pouco mais
avançado, a primeira complexidade é quando a base é negativa. Você sabe já o que que é base. A base é um número que tá ali embaixo, né? Então quando a base é um número negativo. Então vamos supor, por exemplo, que eu tenho aqui 3 elevado 2. Todo mundo sabe que isso aqui dá 9. É o 3 vezes ele mesmo duas vezes, né? Então a gente tem aqui que dá 9. Perfeito, sem problemas aqui. Mas e se fosse aqui o -3 elevado 2? A primeira coisa, você não tem que decorar uma propriedade sobre isso. Você tem
que ter ciência de que esse expoente dois aqui, ele tá justamente localizado em cima do três. Então, quem é que tá ao quadrado? É só essa pergunta que você tem que fazer. Quem é que tá elevado a dois? É o três, galera. Não é o menos. Não é o menos, é só o três, tá? Esse dois aqui, ele tá incidindo. Incidindo. Quer dizer, vamos sempre usar um vocabulário bom aqui, tá bom? Ele está incidindo, ele está atuando apenas no três e não no -3. O menos ele, é claro que o menos, Pedro, mas o menos
não é do três, é o menos ele tá aqui do lado do três, mas ainda assim não quer dizer que o expoente esteja englobando tudo isso, tá? O expoente de fato aqui, o expoente dois só tá atuando no três. Então o que que você tem que fazer? Tem que só visualizar o 3 elevado 2, tá bom? Tem que ignorar aqui o sinal nesse caso e dizer quanto é 3 elevado 2. É 9. Sim, é 9. Agora, e esse sinal aqui? Esse sinal continua aqui, acabou, tá? Quanto é 3 elevado 3? É 27, né? Porque é
o três vezes ele mesmo três vezes. Eh, OK. E quanto é -3 elevado 3? Então, já começa que não é o -3 que tá elevado a 3, é - 3 elevado 3. Não é -3 elevado 3. É menos. É óbvio que na prática não dá para saber a diferença, mas é só paraa tua mente entender, né? Quem tá elevado a 3 aqui é a base 3 e não é o -3. Beleza? Você já vai entender porquê. Então o que que você vai fazer, né? Quanto é 3 elevado 3? É 27. E esse sinal aqui? Tá
aqui ainda normal, não muda nada. Já tem gente aí perguntando: "E se isso aqui for ímpar? Se for par, não muda nada. Se for -3 elevado 4, -3 el 5, vai dar sempre a mesma coisa. Quanto é 3 elevado 4? 81. Mas e esse menos aqui? Tá aqui. Quanto é 3 elevado 5? 243. E esse menos que tá aqui, ele tá aqui ainda. Acabou. Pegou? É só isso. Esse é o primeiro caso e você acabou de aprender ele com solidez. É. Então, ó, eu quero que também você saiba nomear o caso. Pode parecer bobeira, mas
eu quero que você nomeie. O que que é isso aqui? É uma potência de base negativa. Potência de base negativa, só isso. É diferente de uma situação em que você tem uma potência de base negativa, porém você tem uma potência de base negativa e existe a presença de um elemento de parêntese nela. Então, por exemplo, aqui eu tenho uma base negativa que é o -3, assim como eu tinha antes. Quando eu botei -3², eu só fiz 3², que dá 9, e repeti aqui o sinal de menos. Mas quando eu tenho -3 a quadrado, esse a
quadrado agora ele tá incidindo sobre toda a estrutura, ele tá incidindo tanto sobre o três quanto sobre o menos. E o que significa ao quadrado? O que significa uma potência expoente dois? Ela significa o seguinte: olha, essa coisa deve ser multiplicada por ela própria duas vezes. Mas de que coisa ele tá falando? Não é mais apenas do três. A coisa da qual ele está falando é de todo o -3. Então, se você fosse destrinchar isso aqui, você ia ter que fazer assim, olha, é o -3 vezes ele mesmo duas vezes. Só que para você fazer
essa multiplicação, como já foi visto, né, nas aulas anteriores, na semana um, você tem que fazer primeiro o sinal. Quanto é menos vezes menos? Menos vezes menos é mais. Lembra que um menos inverte o outro? Então eu tenho menos vezes esse menos faz com que ele vire mais, né? Um menos inverte sinal do outro, tá? E 3 x 3 é o quê? É 9. Então deu mais 9. Aí você vai falar assim: "Ah, entendi, Pedro." Então, antes dava -9, agora dá + 9. Então, quando tem o parêntese, isso fica positivo, não necessariamente, porque se fosse
-3 todo mundo elevado a 3, o que que eu estaria querendo aqui? Essa estrutura inteira vezes ela própria três vezes. Então eu ia est querendo o -3 x o -3 x o -3. Só que quando você faz menos com menos, dá mais. Agora que tu tem mais, tu faz mais vezes menos, dá menos. O mais não consegue inverter o sinal desse outro menos. Ou você pode pensar que o menos inverte o sinal do mais e ele fica menos. Que seja, né? Então menos com menos mais. Agora mais com menos dá menos. Então o sinal aqui
vai ficar menos. E aí o 3 x 3 dá 9 x 3 dá 27. Então você vê que agora o sinal ficou negativo. Se você tiver aqui agora -3 elevado 4, tu tem aqui o -3 x o -3 x o -3 vezes o -3, né? É o -3 vezes ele próprio quatro vezes. Menos com menos, mais com menos, menos. Menos com menos, mais. E aí o resultado aqui numérico a gente já sabe que é 81. Então agora deu mais, né? Então o que que acontece aí? Cria-se uma regra, né? cria-se uma previsibilidade que é o
seguinte: quando eu tenho uma potência de base negativa e essa potência de base negativa, essa potência de base negativa, ela está toda entre parênteses elevada a um expoente, se esse expoente for um número ímpar, o resultado final vai dar negativo. E se esse expoente for um número par, o resultado final vai dar positivo. Beleza? Essa é a regra, porque como o menos atua como um inversor, a presença de um número menos de um sinal negativo, ela sempre vai ser negativo. E a presença de dois menos com menos vai dar positivo. Mas aí quando você já
tiver o positivo e tu botar o terceiro, vai voltar a ser negativo. E agora quando tu botar o quarto, vai voltar a ser positivo, tá? Então você vai ver que nos casos em que a gente tinha aqui toda, lembrando, tem que ser toda a potência entre parêntese, né? Porque nesse primeiro caso aqui em que não há um parêntese, é irrelevante dizer se isso aqui é par ou se é ímpar. Isso não muda nada. Se isso aqui é parímpar, esse sinal aqui ele não vai ser afetado. O parêntese claramente afeta esse sinal. E aí quando tem
aqui o parêntese, se esse expoente for um número par, tipo 2, 4 6 8 número par, isso quer dizer que o sinal final vai ser positivo, tá? Aqui embaixo ele também é par e o sinal final foi positivo. Mas se ele for ímpar, o sinal final com certeza vai ser negativo. Beleza? Então para fechar aqui a demonstração, se eu tiver aqui menos ã -2 elevado a 7, beleza? Eu já sei que no final, com toda a certeza, o expoente vai ser negativo. E eu sei que 2 elevado a 7, ó, qu 2 4 8 16
32 64 128. Então vai dar -18, tá? E é claro, vai ser o -2 vezes ele próprio sete vezes. Então vai ter o menos sete vezes se multiplicando. Então menos com menos mais vezes menos menos vezes menos mais vezes menos menos vezes menos mais vezes menos, menos menos. Então vai ficar negativo. Mas eu não preciso ficar fazendo isso, né? Porque eu já sei agora que, olha, é um parêntese negativo, é um parêntese e envolvendo toda uma potência de base negativa, inclusive o seu sinal negativo submetido aqui a um expoente ímpar. Então o sinal final precisa
ser obrigatoriamente negativo. Beleza? Acabou. Acabou. Então o primeiro caso aqui tá explicado. Agora sim a gente vê aqui, né, que eh agora sim a propriedade faz muito sentido, né? Quando a gente pensa agora aqui, ó, ã, vamos agora começar a sintetizar isso aqui assim, né? Quando a gente pensa, olha, eh, o número x elevado a 2, ele é a mesma coisa que o xes o x, né? Se eu tiver agora o número - x elevado 2, eu só vou colocar aqui o menos e aí vou colocar o xzes o x do mesmo jeito. Não sei
se vocês perceberam aqui a demonstração assim aritmética, né, que o que que eu quis dizer? Olha, eu vou primeiro lidar com esse x aqui ao quadrado. Primeiro eu vou fazer isso. E lembra que x² é isso aqui? Então tá aqui, ó. Eu isolei entre parênteses para ficar organizado. Primeiro x x. Depois que você tiver resolvido tudo, depois que você souber já a resposta, o sinal de negativo vai estar aqui te esperando. É isso. Independente do que aconteça. Beleza? Agora, se você tiver aqui, né, o -x em si ao quadrado, a gente sabe que isso significa
o -x o -x. Se você tiver aqui o -x em si a cubo, isso significa o -x o -x o -x. Pode parecer besteira, mas isso aqui já é o treinamento de logaritmo de análise combinatória. Você pode ter certeza que você vai entender isso mais paraa frente, tá? É isso. Primeiras propriedades estão aqui. Agora vamos lá. Qual é o próximo caso estranho que poderia aparecer aí na nossa frente, né? Ah, o próximo caso estranho com certeza é estar elevado a um expoente que esse expoente em si é negativo. Então, que que acontece, Pedro? Se eu
tenho um número que tá elevado a um expoente, que o próprio expoente é negativo. Então, sei lá, eu tenho aqui o três, só que ele tá elevado, vamos colocar aqui, eu tenho aqui o nove, né? Só que ele está elevado a -2. O que eu faço com isso? Como eu lido, Pedro, com esse tipo de caso? Como que eu posso fazer aqui? Então, primeira coisa, não, você não vai conseguir eh lidar com esse caso assim diretamente. Por exemplo, quanto é 9 elevado -2? Cara, não tem uma resposta direta para isso. No não, eu quero dizer
assim, não tem um cálculo mental para tu fazer assim, ó. 9 elevado -2 é ele vezes ele mesmo menos duas vezes. Isso não faria nenhum sentido. Isso não faria nenhum sentido. Beleza? Então o que que você precisa fazer? Primeira coisa é você visualizar que você sempre pode dizer que qualquer número, você sempre pode dizer que qualquer número que exista, ele tá dividido por um. Não é problema algum você dizer isso, né? Você pode visualizar isso, tá bom? Que ele tem essa estrutura aqui, né? E aqui em cima também você pode dizer que tem um multiplicando
ele. Não faz diferença alguma, né? Eh, uma Ah, eu tenho 9 elevado a -2, tá? Eu tenho uma vez o 9 elevado -2. É, é o que eu já tinha, dividido por 1. É o que eu já tinha. Isso aqui é só para te ajudar a entender o raciocínio. Mas na prática a gente não vai ficar olhando para isso. Na prática, eu não queria que vocês pensassem isso. Eu tô botando aqui só para explicar que tenha tanto um em cima quanto um embaixo que não muda nada, tá? você vai ter que visualizar essa estrutura, essa
potência do 9 elevado -2 e você vai ter que jogála lá para baixo, porque existe uma propriedade que diz o seguinte: você pode pegar toda uma potência, né, ou seja, a base e o expoente dela juntos e você pode jogar ou para baixo de uma fração ou para cima, desde que na hora que você fizer a transferência você inverta o sinal dos pointes. Então, por exemplo, eu tenho aqui 1 dividido por 1. Isso aqui não muda nada, só tá aqui para enfeitar. Tá vendo? 9 a -2 que tava aqui, ele vai para baixo, ele vai
como 9 elevado a 2 para baixo, tá? É óbvio, esse um aqui você não tem que ficar visualizando ele, né? Nesse caso aqui é só bom você visualizar o de cima para você não se confundir. Ou seja, você vai ter um dividido ai Pedro, cadê um de baixo? Não faz diferença alguma, cara, né? Não faz. Então aqui, ó, tu tem 1 dividido por quem? Pelo 9 elevado 2. Isso sim é uma coisa possível, porque 9 elevado 2 é 9 vezes ele mesmo duas vezes que dá 81. Então você tem 1 div por 81. Então, na
verdade, né, aquela potência, quando você olhar assim, ó, pô, eu tenho aqui, Pedro, 9 elevado -2. O que que eu faço com isso? O que você faz é isso aqui, ó. Você diz que ela é 1 sobre 9 a 2. Você pegou 9 a -2 e jogou para baixo como 9 elevado 2, inverteu o sinal, tá? E acabou. Você já já resolveu agora, tá? Beleza. E isso aqui vale 1 div por 81. Claro que 1 dividido por 81. Ele fala assim: "Ah, mas eu posso tirar esse um daqui?" Não, se você tirar não vai fazer
mais sentido, né? Ele tava ali em cima, ele só tava invisível, porque o quando ele tá do lado do nove ou de qualquer coisa, ele não precisa aparecer, mas quando você tira é bom que ele apareça, né? Senão você vai se perder a conta, né? Então já tinha ali um de fato. Beleza? Eh, é isso. Agora é perguntaram aqui já, né? Quem quer saber assim o mecanismo? Da mesma forma que a gente fala assim, olha, passar pro outro lado, né? Eu vou mostrar aqui o mecanismo mais detalhado, só para ficar legal para vocês, né? Eu
tenho aqui um 9 elevado a -2. O que que eu faço com isso? Aí ele tá dividido por um. E dá para dizer também que tem um aqui. Isso não faz diferença alguma. Como é que eu tô lidando com ele? Eu numa fração eu sempre posso fazer numa fração sempre posso, né, fazer a mesma operação de multiplicação e de divisão em cima e embaixo. Eu sempre posso fazer isso, né? Então eu vou fazer uma multiplicação aqui em cima dessa fração e uma multiplicação aqui embaixo para acabar com esse cara. Mas como é que eu faço
para acabar com 1 9 elevado -2? Eu multiplico ele por 1 9 elevado 2. Beleza? Só que eu tenho que multiplicar também baixo por um 9 elevado 2. Então eu multiplico em cima e embaixo por 9 elevado 2. Beleza? Quanto que é 9 elevado -2 x 9 elevado 2? Vocês e eu ainda não mostrei isso nessa aula, né? Mas eu vou mostrar logo agora em seguida, tá bom? Então, quando a gente tem uma multiplicação de potências de mesma base, eu tô multiplicando potências de mesma base, a base delas duas é 9, a gente repete a
base e soma os expoentes. Só que quanto é -2 com + 2? é zero, ou seja, isso aqui dá 1. 9 elevado a 0 dá 1. Então essa multiplicação aqui de cima, ela deu isso, deu um. Tanto faz 1 x 1, é só um mesmo. E a de baixo aqui ficou só o 9 elevado a 2. Então é por isso que eu posso fazer isso, né? Por isso que eu consegui fazer essa essa operação, tá bom? Então eu vou mostrar aqui só mais algumas vezes antes da gente seguir pra próxima propriedade, né? Ah, Pedro, eu
tenho aqui 4 elevado -3. Na hora você já vai falar isso aqui, na verdade é 1 di 4 elevado 3. Acabou. Acabou. né? É 1 div por 4 elevado 3. O 4 - 3 passou para baixo. Então isso aqui é 1 div por 4 x 4 16 x 4 64. 1 sobre 64. Beleza, Pedro? Eu tenho assim, olha só. 3 x 5 x 2 elevado 7 x 2 elevado 3 x 2 el -5 dividido por 3 elevado -2. vezes 7 elevado a a menos eh 3. Tanto faz. Você pode livremente, de maneira totalmente livre, manipular
qualquer potência que você queira aqui. Qualquer potência, tá? O lembrando que uma potência é o quê? É tanto a base quanto seu expoente. Então, por exemplo, Pedro, eu posso pegar aqui o 7 elevado -3 e passar aqui para cima como 7 elevado 3, invertendo o sinal aqui do expoente? Claro que pode. Tá tudo certo. Ele saiu de baixo para cima. Pedro, esse 2 elevado -5 eu posso passar para baixo como 2 elevado 5? Pode. De -5 ele virou 2/5. Tá certinho? Esse 3 elevado -2 eu posso jogar aqui para cima como 3 elevado 2 invertir
o sinal do expoente? Claro que pode. Tá tudo certo. Agora você vai conseguir resolver com muito mais facilidade. Percebeu? Qualquer potência que você quiser mandar para cima ou para baixo, você pode mandar ela sozinha, sem mexer nos outros. só a própria potência mesmo e desde que você inverte o sinal dela. Então tinha gente ainda que tava com dúvida nisso, né, de olha, eu preciso ter potências de mesma base. Não, qualquer potência faz isso livremente, tá bom? Por quê? Porque a gente não consegue trabalhar com esse com esse point negativo. Esse é o mecanismo que você
tem que ter em mente. Não dá para trabalhar com esse poente negativo. É muito difícil. Não tem o que fazer com ele diretamente, né? Você tem que sempre, se ele tá em cima, passa para baixo e deixa positivo. Se tá embaixo, passa para cima e deixa nega e deixa positivo. Beleza? Próxima propriedade que era para eu ter até falado antes, porque ela é muito mais básica, né? Que é o seguinte, multiplicação, tá? De potências de mesma base. Então, por exemplo, eu tenho aqui, ó, 2 elevado 7, né? Vamos fazer com uma mais baixa primeiro. Eu
tenho 2 elevado 3 x 2 elevado 2, né? Como é que eu lido com isso, tá? Eh, primeiro, né? Se você abrir ela, você vai perceber o que que é o 2 elevado 3. Ele é o 2 x 2 x 2. Só que isso vezes o 2 elevado 2. O que que é o 2 elevado 2? Ele é o 2 x 2, tá? Então quantos número dois eu tenho aqui se multiplicando por eles próprios? Eu tenho cinco. Então é claro que isso aqui é o quê? Eu posso escrever tudo isso aqui como sendo 2 elevado
a 5. É verdade total, né? 2 elevado a 5 é justamente o dois vezes ele próprio cinco vezes seguidas, tá? Então, por isso que eu posso escrever isso. Daí que vem a propriedade de, olha, quando você tá fazendo multiplicação de potência de mesma base, e olha que a base das duas é a mesma, você pode repetir a base uma vez, deixar o dois aqui e somar os expoentes. Quanto é 3 + 2? É 5. Tá bom? É isso. Então, viu que viu ali que deu o mesmo resultado, né? Que vai ser, no caso, 328 16
32. É isso mesmo. Tá bom? Então, eu tenho ali, ó, 7 elevado, vamos fazer agora aqui, eu tenho assim, ó. 3 elevado 3 x 3 elevado 4 x 2 elevado 3. Que que eu posso fazer aqui? Ué, eu tenho aqui potências de mesma base nesse primeiro caso aqui. Então aqui eu tenho três, eu vou repetir a base 3 e somar os expoentes, que é o 3 e o 4. Então isso aqui é 3 elevado 7 x 2 elevado 3. E agora, Pedro, como que eu resolvo isso aqui? Não tem nenhuma propriedade que você possa usar
aqui. Você tem que descobrir o valor desse cara e multiplicar pelo valor desse cara, que é 8 2 elevado 3, agora 3 elev 7, vai dar um número bem maior, tá? Eh, mas é isso. Mas agora essa daqui já é a resposta sintética. Se quiser saber o valor de fato que isso aqui dá, só multiplicando, não tem uma uma propriedade, tá bom? Para isso não. Quem chegou agora pode continuar vendo, fica tranquilo, tá? Todo mundo tá tá pegando. É isso, né? Agora, Pedro, se eu tiver assim, olha, 2 elevado 7 x 2 el -2 x
2 el 4. Potências de mesma base. Você repete a base, que é dois, né? A base de todos é dois e somos expoentes. Eu tenho sete, eu também tenho quatro. Eu tenho 11 no total, mas eu tenho -2. Então quando você bota uma dívida, tu tem 11, mas tu perde dois, você fica com, né? Então esse -2 é uma dívida, tá bom? É poder ter feito sete. Aí -2 fica 5. Aí o 5 mais o 4 dá 9, dá no mesmo. Tá bom? Aí você fala assim: "Pedro, mas pera aí, você me disse que o
expoente negativo eu deveria passar para baixo, não é isso? eu deveria passar para baixo invertendo. Cara, você também pode fazer isso. É que nesse caso aqui acaba sendo mais conveniente eu já somar, acaba sendo sendo legal, né, a gente fazer assim. Concorda comigo? Porém, né, eh, a gente poderia ter feito de outro jeito. Então, por exemplo, a gente pode, lembra que deu 2 a 9, né? Então, vamos lá. Deu 2 a 9, a gente pode eh é exatamente o problema é quando a potência tá sozinha negativa, aí não tem o que fazer. Você já passa
para baixo inverte sinal. quando ela tá junto com outras potências de de mesma base, é bem provável que a gente consiga eh somar, né, multiplicar essas potências e somar os expoentes e aí vai resolver, tá? Agora tenho aqui essa estrutura e eu tenho que imaginar que ela tá dividida por um. Sempre pode dizer que tá dividido por um. Sempre não muda nada, né? Eu se eu pegar esse 2 elevado -2 e passar para baixo, né? Aí ele vai para baixo como quê? Como 2 elevado 2 e ele sai aqui de cima. Então 2 elevado 7
x 2 elevado 4 dá 2 elevado 11 e dividido por 2 elevado 2. Isso aqui cai na outra propriedade que na verdade não tem nada de novo nessa outra propriedade que eu vou mostrar agora, né? Ela é a propriedade de sempre, tá? Que é o seguinte, eu tenho aqui 2 elevado a 11. Eu tô falando aqui de uma divisão de potências de mesma base, né? Tá vendo que a gente tá fazendo uma divisão de potência de mesma base? Estamos, né? Estamos dividindo potências e elas têm ambas a base dois. A regra é repete a base
e subtrai os expoentes, né? Então fica aqui, ó, 11 - 2, né? Então 2 elevado 11 - 2 é 2 elevado 9, tá? Deu a mesma resposta de antes, tá? Você também poderia visualizar, falar o seguinte: "Não, agora eu decidi que eu quero pegar o 2 elevado a 2 e passar para cima como 2 elevado a -2. Tá bom? Repete a base soma dos expoentes. 11 com -2 dá 2 elevado 9 do mesmíssimo jeito que dava antes. Beleza? Então mais uma teoria aí demonstrada, né? provada, solidificada na nossa cabeça, tá bom? Eh, isso se aplica
muito, né? A gente usa muito isso nas potências ali de base 10, né? Então, a gente tem 10 elevado 3 x 10 elevado 8, a gente já diz: "Olha, isso aqui é 10 elevado 11", né? E assim vai. Mas enfim, é a mesma propriedade sempre, tá bom? Quando eu vejo uma divisão de potências, então eu tenho aqui, ó, 4 elevado 5 div por 4 elevado 3. Ou você repete a base subtra expoentes, ou você pode pegar e puxar isso aqui para cima, né? E ficar 4 elevado 5 vezes, né? Isso aqui tava dividindo, vem multiplicando
4 elevado -3. De modo que repetindo a base, somando expoênes, a gente tem 4 elevado 2. Beleza? 5 com -3 dá 2. Ok? Pronto, né? Legal. É, agora tem também assim, se quiser enxergar dessa forma, né? Pô, Pedro, eu tenho aqui, lembra aquele exemplo? Era 2 elevado 7 x 2 elevado -2 e x 2 elevado a como é que tava antes? Tava a qu tava assim no exemplo anterior, né? Se tu quiser também você pode enxergar assim, olha, passei esse 2 elevado a -2 para baixo como 2 elevado a 2, tá? Agora o que que
é isso aqui, né? Por que, vamos supor, o de cima eu já vou deixar aqui e como 2 a 11 e embaixo dividido por 2 a 2. Você pode enxergar também que, olha, o que que é 2 elevado 11? É 2 x 2 11 vezes e 2 elevado 2 é o quê? É 2 x 2. Então você pode pegar esse dois aqui, dividir com esse aqui, né? Então, divide por dois, divide por dois e divide por dois, divide por dois. Sobraram quantos aqui em cima? Sobraram justamente nove, né? 2 elevado a 9. Beleza? Por isso,
tá? Tá tudo assim sempre bem sólido, bem interconectado, tá bom? Próximo desafio que pode acontecer é um expoente fracionário, né? Então, quando a gente tem aqui, por exemplo, 9 e aí esse 9 tá elevado a 1 sobre 2, Pedro, quando ele tá elevado a um número negativo, eu posso jogar ele para baixo e deixar o expoente positivo, né? Fica 1 dividido por 9. Tá, mas e agora que o expoente é uma fração, o que é só você pensar assim, o que que seria 9 vezes o 9, mas pera aí, quantas vezes? Meia vez, cara. É
até difícil de você imaginar o que que significa isso. É o nove vezes ele próprio, mas o nove vai ser multiplicado por ele mesmo apenas meia vez, né? Isso é muito complicado, tá? Não, não. É, às vezes você vai pensar: "Não, isso é o 9 vezes o meio, é o 9 dividido por 2, não é, é o 9 vezes o próprio 9, mas quantas vezes isso acontece?" Apenas meia vez, galera. Nem eu consigo abstrair o que que é isso, tá? Então, qual é a regra para lidar com o expoente fracionário, tá? Não, não é 9
x 4,5 falando não, não é isso não é o 9 vezes ele mesmo meia vez, isso é o 9 x metade de 9. É para você multiplicar o nove por ele mesmo. Mas quantas vezes é para tu fazer isso? Só meia vez. Como é que você multiplica o nove por ele mesmo? Mas duas vezes, três vezes? Não, meia vez. Faz isso só metade de uma vez. Sacou? É bizarro. Você não consegue abstrair o significado prático disso, tá? O que que você vai fazer na mesma hora, tá? Você sempre vai olhar para esse point fracionário e
você vai lembrar de uma toalha de mesa, tá? Pensa numa toalha de mesa. O que que acontece quando você, ó, puxa uma toalha de mesa, né? Aqui, ó, quando você pega uma toalha de mesa e puxa essa toalha de mesa, as coisas que estão em cima dela fazem o quê? Então, aqui, ó, tenho aqui uma xícara, ó, minha minha mão é a toalha. Beleza? Vamos fazer aqui agora, ó. Eu quero que você pense aqui, ó, na minha na minha orelha, ó. Eu vou pegar a minha mão aqui e vou trazer pra minha orelha, ó. Ó,
você entendeu aqui, Ó, a minha mão veio para cá e a xícara caiu. Essa visualização ajuda bastante, tá bom? Ajuda realmente bastante. Então, eu quero que você pegue aqui o dois e você puxe ele para cá. Óbvio, quando você puxar ele para cá, primeira coisa é que o um vai cair. Então, aqui, ó, o nove tá aqui. Aí, tá vendo esse um aqui, ó? Quando você puxa o dois para cá, o escorrega e fica aqui. E esse dois vem para onde? Esse dois vem para cá. Essa parte aqui do denominador vira na verdade o índice
de uma raiz, tá? O que que é isso, né? Isso aqui, esse índice aqui, geralmente ele não aparece porque raiz quadrada a gente não coloca o dois aqui, mas eu tô botando só para mostrar, beleza? Ã, o que que é primeira coisa, né? 9 elevado a 1 é o próprio 9, né? O que que é a raiz quadrada de 9? Que tipo de pergunta é essa? A raiz quadrada 9, a pergunta é o seguinte, ó. Qual é o número que vezes ele mesmo duas vezes dá o 9? E a resposta é três. O três vezes
ele mesmo duas vezes dá o nove. Beleza? É o que eu falei, tem gente que usa o negócio de, olha, quem tá na sombra vai pro sol porque ele tá no sol aqui. E quem tá no sol vai pra sombra porque agora ele tá na sombra. Mas eu acho que é um macete inferior. Eu acho que é é uma historinha que você acaba tendo que contar. E eu não acho que seja uma boa forma você lidar assim. Eu prefiro só que você vê, mas se quiser também lidar assim, fica à vontade. Mas eu só puxo,
beleza? Eu só puxo, eu só tiro esse cara que tá aqui e visualizo que o expoente vai cair sempre, tá? Então, na verdade, o 9 elevado a meio é o quê? É a raiz quadrada do 9 elevado a 1, que é a√ qu 9 dá 3. Beleza? Só isso. Vamos lá. Eu tenho aqui o número 16, deixa eu colocar aqui, sei lá, ó. Tenho aqui o número 27 elevado a 1/3. Pedro, como é que eu lido com 27 elevado 1/3? Meu Deus, né? Ele está elevado a 1/3. 27 vezes ele próprio 1/3 de vez. Galera,
não posso responder pergunta na hora da aula não dá. Olha só, 20, eu respondo já que muita coisa do chat tem umas perguntas falada, não consigo. Então, olha só, 27 elevado 1/3. Que que eu pego? Eu pego esse expoente aqui, essa o denominador da fração e puxo para fora. Quando eu puxar, ele vai vir para cá. Então vai ficar assim, olha. Ra cúbica de 27. E esse um aqui cai aqui. Mas nesse caso aqui, esse 1 também não tem relevância, porque 27 elevado a 1 é o próprio 27. O que é raiz cúbica? Raiz cúbica
pergunta é a seguinte: "Olha que número eu quero saber qual é o número que vezes ele próprio três vezes, né? Porque é uma raiz cúbica. Então que vezes ele para três vezes dá o 27. É o próprio três, né? 3 x 3 x 3 dá o 27. Beleza? Então Pedro, eu tenho aqui agora, ou seja, não é o 27 elevado 1/3, na verdade ele é 3, tá, Pedro? Eu tenho aqui agora ã oito, é que eu tô inventando os exemplos agora, né? 8 elevado a 2/4, né, Pedro? 8 elevado a 2/4. Primeira coisa, Pedro, eu
posso pegar o 8 elevado a 2/4 e chamar ã esses 2/4 de 1/ 2? Pode. Você pode com certeza vir aqui nessa fração e falar assim: "Cara, isso aqui é a mesma coisa que 8 elevado a 1/ 2." Pode, mas vamos fazer das duas formas. Eu vou mostrar para vocês só para fortalecer o raciocínio matemático da turma, tá bom? O que seria um 8 elevado a 2/ 4, né? Eu teria que pegar esse quatro aqui, você concordar para fora, né? Então vamos fazer isso, ó. Eu pego aqui esse quatro e puxo para fora. Então qu,
né? De quem? de 8 elevado 2, tá? Quem é o 8 elevado 2? É o 64. Já vou resolver aqui, né? E aí a pergunta é essa. Quarta de 64. Então a pergunta ficou sendo a seguinte: qual é o número que vezes ele mesmo quatro vezes dá o 64? Um número que vezes ele próprio 4 vezes d 64, né? No caso aqui eu criei o exemplo errado porque não tem uma raiz exata, uma raiz qu exata do 64, né? Eu tava eu tava pensando era para fazer aqui, ó, é o 2/3 mesmo, tá? Vamos colocar
aqui o 2/3 para dar certinho, tá bom? Então aqui, ó, 8 elevado 2/3, né? Então você puxa o 3 para cá, fica o quê? Olha, eu quero a raiz cúbica de 8 elevado 2. 8 elevado 2 dá quanto? 64. Então, quem é a raiz cúbica, né, de 64? Ou seja, qual é o número que vezes ele mesmo três vezes vai dar 64? é o 4. Dá 64. Beleza? Acabou, tá? Então tá resolvido aqui mais uma situação que aparece aí, né, que a gente consegue lidar com ela dessa forma. A gente nos treinamentos aqui, né, que
a gente tem uma lista de exercício imensa pra gente fazer, a gente vai fazer isso eh ostensivamente, né? A gente vai fazer bastante bastante bastante, tá bom? Perguntar se a raiz a raiz quarta do 64 não era o 4, não. Porque 4 vezes ele quatro vezes não dá 64. 4 x 4 x 4 x 4 vai dar 256. Beleza? OK. A√ quarta de 64 ela não é 4. Não tem raiz quarta. É, tem, mas vai ser quebrada, entendeu? Não vai ter um número, um número eh, não vai ter um número exato pra√ quarta de 64,
mas pra raiz cúbica de 64 vai ter, entendeu? Deixa eu pensar aqui em um que tem uma uma raiz quarta fácil da gente achar. É o próprio próprio 16, né? Então, por exemplo, se eu tiver assim, olha, vamos lá. Se eu tiver aqui 4 elevado 2/4, tá? E aí eu vou fazer tanto assim quanto no exemplo em que eu simplifico aqui o expoente, beleza? 4 elevado a 2/4, eu vou primeiro puxar a fração para trás, né? O então vai ficar 4. Aí esse 4 vem para cá, né? Então eu quero a√ quarta de 4 elevado
2. Mas 4 elevado 2 é 16. Então eu quero aqui a√ qu. A pergunta é que número vezes ele mesmo quatro vezes dá o 16? 2. Tá? E aí você percebe, né, que na verdade a radiciação é realmente o contrário da potenciação, beleza? Porque quando eu digo assim, olha, pensa só nessa estrutura aqui agora que eu vou marcar, tá bom? Isso aqui é uma verdade, você concorda? Você visualiza comigo que isso aqui é uma verdade? Qu 16 a 2. Porque a raiz qua essa é a pergunta. Que número vezes ele próprio quatro vezes dá o
16? Dois, tá? Se você pegar aqui o índice, tá vendo aqui o índice e jogar ele aqui para cima, transformando em um expoente, ó, esse quatro vai sair daqui, galera, e vai vir para cá, ó, e vai sumir aqui essa estrutura. Óbvio, não continua sendo verdade? 2 elevado 4 não é o 16, não é isso? Por exemplo, eu tenho aqui, ó, 2 elevado 3 = 8. Você concorda? Eu não posso pegar esse expoente três aqui e jogar pro outro lado, tá? Mas qual é o oposto? Qual é o inverso da da potenciação? é a radiciação.
Então, quando eu pegar aqui esse esse expoente cúbico e jogar aqui, ele vai, mas ele vai como um índice de raiz. Aí eu te pergunto, a raiz cúbica de 8, o número que vezes ele próprio 3 x 8 não é o próprio 2? Visualizou? Se eu tivesse aqui antes, Pedro, e se antes eu pegasse esse expoente fracionário e simplificasse, então 4 elevado 2/ 4 é a mesma coisa que 4 elevado 1/ 2. Perfeito. Pega agora essa esse denominador e puxa para fora. O que que você vai ter? você vai ter √ qu elevado 1, que
é o próprio 4. Quem é a √ quadrada 4? É 2. Mas a resposta antes também não era 2. Essa resposta aqui tava dando justamente dois. A mesma coisa. Então é óbvio, se eu puder simplificar a fração, eu vou fazer isso mesmo, tá? Mas agora duas propriedades de potenciação para vocês, tá bom? Vamos lá. Mais propriedade de potenciação. Essas daqui são bem importantes. Todas são, né? Mas essa aqui são bem bem bem importantes. Tá bom? Perguntaram ali para mim, Pedro, 8 elevado 2/4 ã dá 4√2? Vamos ver, tá? 8 elevado 2 4 é a mesma
coisa que 8 elevado 1/ 2. Tá bom? Então isso aqui eu vou pegar esse expoente, vou jogar para fora. Isso aqui é o quê? √8, né? Nem vou botar de 8 elevado a 1 que dá oito. E também nem vou botar o dois aqui, porque quando a gente tem raiz quadrada, a gente não bota o dois aqui, porque a gente se só de ter a raiz assim, a gente já sabe que tem um dois ali. A gente só marca mesmo quando é uma raiz maior, tá bom? Então ele perguntou assim: "O 8 elevado 2/4 é
a mesma coisa que 4√2. Vamos ver. quad 8. Você sabe qual é? Eu não sei que número vezes ele próprio duas vezes dá 8. Nem um número vezes ele próprio duas vezes d 8, né? 2 x 2 dá 4, 3 x 3 dá 9. Então que que a gente faz aqui dentro? Ó, eu não sei quanto é a√8, Pedro. Tá? Então tenta quebrar ela um pouquinho. Por exemplo, √8 não é a mesma coisa que √2 x 4? É mesma coisa que √2 x 4, né? Tá. Você sabe a √2? Não. É, é quebrada, né? 1,41,
mas eu vou fingir que eu não sei. Você sabe a √4, a √4 é 2. Então, já que a √4 é 2, eu vou tirar aqui o valor, né? Então, √4 é 2. Então, eu consigo responder essa parte aqui. Porque, galera, esse negócio de √2 x 4 é a mesma coisa que isso aqui, ó. √2 x √4. Só que a √4 eu sei que a resposta é o quê? 2. Então acaba que quando eu tenho essa estrutura aqui, olha só, √2 x 4, eu pego o 4, dou a resposta e jogo a resposta dele para
fora. A resposta do 4 é do e aqui dentro√2 eu não sei. Então você tava errado. É 2√2, mas o menino tinha perguntado se era 4√2, não é 2√2, entendeu? Perguntaram ali para mim assim, ó, Pedro, eu não sei falar todas as propriedades na ponta da língua, mas eu consigo lembrar nas horas na hora dos exercícios. É normal? É normal, mas está errado, tá? Eu também não sei falar todas as propriedades na ponta da língua, mas eu começo pela primeira propriedade, eu puxo todas. você tem que saber fazer o que eu fiz nessa aula. Você
tem que saber puxar todas as propriedades. E aí, na verdade, é óbvio que na verdade eu sei falar todas na pontra língua, mas é só porque eu já fiz isso várias vezes, mas você tem que puxar todas, entendeu? OK. Eh, então isso aqui agora eu tô eu vou eu vou dar uma aula ainda teórica mais aprofundada em radiciação, tá bom? Mas isso aqui agora foi só uma demonstraçãozinha, porque o menino ali perguntou, eu quis responder ele, tá? Então, olha só, outra propriedade de potenciação agora que eu vou demonstrar aqui para vocês é o seguinte, tá?
Quando eu tenho 2 elevado a 3, isso vale 8, tá? E se agora eu colocar aqui um parênteses e aí eu colocar aqui elevado a 4? Quanto que isso dá? De cara você tem que falar assim: "Olha, isso aqui dá 2 elevado a 12, tá? Porque você vai multiplicar o 3 pelo 4", tá? Mas por que que isso funciona? Porque pensa comigo, tá tudo ancorado no mesmo princípio básico de potenciação. O que que é esse quatro aqui? Esse quatro quer dizer, olha, essa estrutura inteira que tá dentro do parêntese, porque o parêntese de o parêntese
determina que a incidência da potência de que do expoente 4 é em todo mundo que tá dentro do parêntese. Então o quatro não tá incidindo apenas e no três, não. O quatro tá incidindo no parênteses inteiro, no 2 elevado a 3 inteiro. Então na verdade é o 2 elevado 3 vezes ele mesmo. Quantas vezes? Quatro vezes. Certo? Só que pra gente fazer a multiplicação de potência de mesma base, a gente repete a base e soma os expoentes. 3 + 3 + 3 + 3, que dá 12. Beleza? Perguntar, então por que que não é o
2 elevado a 4? Porque o que eu falei, o 4 não tá atuando só no 2. O 4 tá atuando no 2 elevado 3. Então esse 4 tá dizendo é o 2 elevado 3 vezes ele próprio quatro vezes. Então é o próprio 2 elevado a 3 que vai ter que ser multiplicado por ele próprio quatro vezes. Beleza? E foi o que foi feito aqui. E aí dá 2 elevado a 12. Então, a gente tem aí uma consolidação mais rápida, né, da gente só multiplicar isso aqui. Quando a gente pega o 3 x 4, a gente
multiplica. Porém aqui que vem o detalhe, né? O detalhe é o seguinte, tá? Quando a gente tem assim 2 elevado 3 elevado 4, isso é muito diferente, muito diferente, porque tá vendo esse point 4 aqui? Me diz uma coisa, em quem ele está incidindo, galera? Ele na verdade só tá incidindo no três. Esse expoente quatro ele é um expoente do expoente. Então esse quatro tá atuando só no três. É diferente daqui em que o quatro atua em todo mundo. Aqui o quatro atua em todo mundo, né? Então qual dos dois vai ser maior? De cara,
né? O maior vai ser o primeiro ou o maior vai ser o segundo? Quem vai ficar maior? O primeiro em que o quatro atua em todo mundo ou o segundo, né? Em que o quatro atua somente no três, né? O maior é o segundo, tá? Por incrível que pareça, porque no caso do segundo aqui, eu tenho 2 elevado a quem? A um 3 que está elevado a 4. Mas pera aí, deixa eu só entender quanto que é o 3 elevado a 4. É o 3 vezes ele mesmo quatro vezes, né? Então é o 3 x
3 que dá 9 x 3 que dá 27 x 3 que dá 81. Meu Deus do céu, isso é 2 elevado 81. Na verdade, não é o dois vezes ele mesmo 12 vezes, é o 2 vezes ele mesmo 81 vezes. É muito grande, muito grande, né? Sacou? Só quero te fazer uma pergunta. Eu quero que você responda rápido. Quero que você responda rápido, né? Tenho aqui 2 a 10. 2 elevado 10. Beleza? 1 2 3 ou quatro. Quem é o dobro? Responde rápido. Quem é o dobro de 2 elevado a 10? 1 2 3 ou
4. Quem é o dobro? O dobro tá aqui. Muita, muita, muita gente mesmo disse 2 elevado 20. Muita gente. O dobro tá aqui, tá? A 2 a 10 é uma coisa. 2 elevado a 11 é o quê? É a mesma coisa que o 2 a 10, só que tu ainda multiplica por pelo 2 mais uma vez. Então ali você dobrou, tá? O 2 elevado 20 é muito muito muito muito maior, né? O 2 elevado 10 mesmo, ele ele é 1024. E o 2 elevado 11 é o quê? É isso aqui. Só que tu multiplica por
dois de novo, fica 2048. Isso já caiu no Enem, tá? Já caiu mesmo. Beleza? Isso aqui é bem importante, hein? Ok? Então 2 elevado 10 é uma coisa, 2 elevado 11 é o dobro. Entendeu? Ah, um menino falou assim: "Não entendi, vê de novo." Olha isso aqui de novo. 2 elevado 10. Pergunta: "Quem é o dobro? Quem é duas vezes maior do que ele? É o 2 elevado a 11. O bug é justamente você pensar que é o 2 elevado a 20, porque esse expoente aqui é o dobro, né? Cada expoente a mais que eu
boto não é uma multiplicação por dois a mais que eu faço. O 2 a 10 é 1024. O 2 a 11 é o quê? 2048. Que eu boto mais um do ali. Então eu dobro, tá bom? Então perfeito. Vocês viram a diferença, né? Entre você ter ali um parêntese e você não ter um parêntese, tá? Se eu tenho assim, olha, 3, vamos, sei lá, eu tenho aqui 5 elevado 2, né, elevado a 3, isso aqui é o 5 elevado 6. É só fazer o 3 x 2. Ou você falar, é o 5 elevado 2 vezes
ele próprio três vezes. Mas se eu tenho 5 elevado a 2 elevado 3, aí na verdade esse dois aqui, esse expoente 3 tá atando só no expoente dois. Então o 2 elevado a 3 aqui já é oito. Isso aqui já é o 5 elevado 8. Já é bem maior e já é bem diferente, tá? Agora, é claro, todas as regras aqui já foram dadas e elas têm que atuar juntas. Então, podem começar agora a acontecer algumas confusões, né? Então, por exemplo, Pedro, e se eu tivesse, olha, 5 elevado a 2 e aí isso está elevado
a -3, bicho, tranquilamente. Você primeiro multiplica esses dois pointes aqui, como eu já ensinei. Então, quanto é 2 x -3? Ué, mais com menos dá menos. Então, é 5 elevado -6. Agora que tu tem o 5 elevado -6, como é que você lida com esse expoente negativo? Você passa ele para baixo. Então deixa o aqui em cima e deixa 1 dividido por 5 a 6. Acabou. 5 a 6 vai dar um baita número grande, né? Mas é isso, tá? Vai ficar um dividido por um ba, vai dar um numerozinho pequenininho no final. A resposta completa,
né? Eh, ah, faltou uma. Obrigado aí por me lembrar. Muito bom, né? Uma uma faltou essa aqui. É muito boa mesmo. Obrigado aí, me lembraram, né? Eh, então vamos supor que eu tenho assim, olha, 2 x 3 x 5 e eu tenho um parêntese aqui e nesse parêntese eu tenho aqui elevado a 2. Isso quer dizer, galera, que o dois atua em todo mundo que tá dentro do parêntese, tá? Em todo mundo. Então, por exemplo, o que que é isso? Na verdade, tá? Visualiza só. É esse 2 aqui elevado a 2 vezes esse 3 aqui
elevado a 2 vezes esse 5 aqui. também elevado a dois, beleza? Atua em todo mundo. Algumas pessoas aí eu vou mostrar de novo porque eu tenho certeza que algumas pessoas vão confundir com uma coisa que eu vou falar agora. Ninguém falou ainda, mas eu acho que vocês vão confundir com isso, tá bom? Vamos supor que eu tenho aqui. Olha só, 3 x 5 elevado 2. O que que é isso? Isso é o 3 elevado 2 x o 5 elevado 2. Certo? É isso. O expoente do atua em todo mundo. Mas é diferente de eu ter
aqui, olha só, 3 + 5 elevado 2. É diferente de eu ter o 3 + 5 elevado 2, tá? Você não pode aqui de forma alguma dizer que isso é o 3 elevado 2 + o 5 elev 2. Não pode, tá? Pelo fato de você ter essa soma aqui, esses números ainda não estão misturados, eles ainda não estão mesclados. Você não pode fazer isso. Você não pode dizer: "Olha, não, esse dois aqui atua aqui e atua aqui." Não pode, tá? Não pode. Beleza? Aqui, nesse caso, quem é que tá elevado a dois? Entenda bem, quem
tá elevado a dois é toda a estrutura desse parêntese. Claro que você poderia somar primeiro. Você poderia fazer 3 + 5 é 8. Isso é 8 elevado 2, né? Eu vou, a gente ainda vai ter uma aula sobre produtos notáveis. Eu só estou antecipando. Então, se você não entendeu o que eu tô falando agora aqui, não é um grande problema, porque eu tô só antecipando um pouco, tá bom? Mas eu só quero dizer que você não pode pegar o dois e aplicar aqui nos dois porque eles ainda estão sendo somados. Eles ainda precisam avançar de
operação, eles ainda precisam se multiplicar, se somar primeiro, né? Agora o que você poderia fazer, né? É o quê? Tá vendo esse parêntese todo? Ele é o 3 + 5, concorda? Ele é o 3 + 5. Ele todo está ao quadrado. Então concorda que ele todo você tem que pegar e multiplicar por ele mesmo duas vezes. Então você pode pegar e fazer assim. Olha só. 3 + 5 x 3 + 5. Aí você pode. Aí você pode, porque quem é que tá ao quadrado? O parênteses inteiro. Beleza? Deu para você entender? O parênteses inteiro está
ao quadrado. Então é ele vezes ele mesmo duas vezes. Só que aí para você fazer isso, você teria que fazer assim. Olha só. Primeiro, cara, você vai multiplicar esse esse cara inteiro por esse cara inteiro. Então você vai pegar primeiro esse terminho aqui, o 3 e vai multiplicar tanto pelo 3 quanto pelo 5. Então vamos lá. Quanto é 3 x 3? 9. E quanto é 3 x 5? 15. Tá? Agora pega esse segundo termo e multiplica por esse por esse. Quanto é 5 x 3? 15. E quanto é 5 x 5? 25. Beleza? Então temos
aqui 15 + 15, 30 + 25, 55 e + 9 a gente tem 64. Beleza? E se antes a gente tivesse somado aqui de cara, 3 + 5 ia dar 8. E esse 8 tá elevado a 2, né? Ou seja, 8 elevado a 2 dá o quê? 64 do mesmo jeito. Então é óbvio que nesse caso aqui valia muito mais a pena eu ter somado direto. Mas é que vocês vão ver no no nos próximos capítulos de produtos notáveis que isso aqui não aparece desse jeito. Aparece sempre aqui, ó, x + y². E ele quer
que tu cometa o erro, ele quer que tu cometa o erro de você colocar o a quadrado tanto no x quanto no y. E na verdade não funciona assim. você precisa realmente pegar o parêntese inteiro do x + y e multiplicar por ele próprio duas vezes, tá? Que é o que diz aqui o sinal da potência, beleza? Ok? Agora, nesse caso aqui em que a gente já tem uma multiplicação, no caso em que a gente já tem ali uma multiplicação, é óbvio que a gente tem duas opções também. A gente pode primeiro resolver a multiplicação.
Então, pera aí, Pedro. 3 x 5 não é 15. Isso não tá ao quadrado. Sim. 15² é 225. Mas nesse caso a gente também pode optar, tá, por distribuir essa potência, né? Então pegar aqui a potência, ela pode ser distribuída dentro de uma multiplicação, né? A gente pode pegar a potência e colocar aqui, olha, o dois tá aqui e tá aqui. Então, na verdade, ó, é o 3 elevado 2 x o 5 elevado 2. O 3 elevado 2 é 9 e o 5 elevado 2 é o quê? 25. E 9 x 25 dá o quê?
225 também. Beleza? É distribuir os expoentes, no caso, não a potência, né? É isso aí. Perfeito. Deu para visualizar? Agora, por que que eu tô explicando isso, né? Eu não vejo muito explicarem essa. O que eu vejo é explicarem direto a potência eh de base fracionária. Mas aí o moleque falou assim: "Pedro, você esqueceu de base fracionária?" Aí eu lembrei justamente, falei: "Então, antes eu vou explicar quando a base é um produto". Beleza? Então agora vamos lá. Quando a base é uma fração, vamos pensar aqui. Olha, eu tenho aqui 3 sobre 4 elevado 2. Agora
sim, tá? Agora sim. Vamos lá. 3 dividido por 4. Mas tudo isso está sobre 2. Primeira coisa, Pedro, eu poderia resolver esse número aqui. Ah, 3/ 4 é 0,75 e ele está ao quadrado. Poderia. E o que que é o 0,75²? É o 0,75 vezes ele próprio duas vezes, tá? 075 x 075. Quanto que vai dar esse número? Alguém faz aí na calculadora, né? 75 de de 75. Multiplicar alguém por 075 é pedir 3/4 dela. 3/4 desse cara aqui vai ser de quatro partes dele. Tem que tirar 0 ponto. É difícil de fazer de cabeça
isso aqui. Dá 0,56. Isso aí. 56 25. Boa. Tá legal. Agora a gente não vai geralmente fazer desse jeito, né? Não faz. Eu só tô fazendo aqui para dizer para vocês que é matematicamente válido executar mesmo essa divisão aqui e depois botar o quadrado. Mas vamos lá. O que que é o mais prático? é você visualizar que esse expoente ele atua tanto no numerador quanto no denominador. Então ele atuando no numerador, o numerador fica 3 elevado 2. E ele atuando no denominador, o denominador fica 4 elevado 2. Beleza? Quanto é 3 elevado 2? É 9.
E quanto é 4 elevado 2? É 16. Se você fizer na calculadora agora 9 di 16, pode ter certeza que vai dar também 0,5625. Beleza? E é óbvio que na hora da prova essa resposta aqui vai aparecer já nas opções. A 9 sobre 16 já vai aparecer dessa forma. Beleza? É isso, tá? Eh, exatamente, né? Se fosse 8 sobre 16 seria meio, né? 8/ 16 daria 0,5, mas é um pouco maior que 89, vai dar justamente 0,56, algo assim. Beleza? Ótimo. Tá? E aí agora tem uma uma propriedade aqui que, cara, ela é realmente ela
é uma evolução dessa aqui, né? Ela ela é uma variação dessa daqui, mas ela é bem importante também, bem importante mesmo, tá bom? Que é o seguinte, vamos supor que eu tenho aqui, ó, ã, 3 sobre 4, só que eles estão elevados a -2. Todo mundo tá elevado a -2, tá? Isso é muito legal. Vamos fazer por partes e depois eu mostro, né, o atalho, a propriedade consolidada. Então, vamos lá. Primeira coisa, é válido dizer que esse -2 ele atua tanto no 3 quanto no 4? Claro, esse -2 incide em todo mundo. Então, isso aqui
é o 3 elevado -2. dividido também pelo 4 elevado -2, tá? É válido eu pegar esse 3 que tá elevado a -2 e passar para baixo e aí eu vou inverter o sinal do expoente? Sim. Então ele vem para cá como 3 elevado 2. E esse 4 elevado -2, se eu jogar para cima, eu também não vou inverter o expoente dele. Então o 4 - 2, quando eu passar para cima, ele vai virar o 4 elevado 2. Beleza? Perfeito. Agora que eu tenho 4 elevado 2 di 3 elevado 2, claro que eu posso resolver. Então
é claro que eu posso Ah, isso aqui dá 16/ 9. Eu sei, eu sei que sim. Claro. Então já tá resolvido. Porém, né, o que que também poderia fazer? Não sei se você lembra, mas quando eu tenho um expoente assim do lado de fora da fração, ele atua em todo mundo. Você concorda? Sim, ele atua em todo mundo. Então, quando eu tenho também o mesmo expoente atuando em todo mundo que tá na fração, eu não posso pegar esse expoente que tá aqui e ao invés de eu escrever dessa forma que eu escrever assim, ó, esse
4 elevado 2 di por 3 elevado 2, na verdade ele é 4 sobre 3, todo mundo elevado a 2. Sim ou não? Totalmente legítimo, né? Totalmente válido fazer isso, né? Então é a mesma coisa, né? Agora se eu reverter, eu vou botar o dois aqui e vou botar o dois aqui, vai ficar de novo justamente o 4 elevado 2 dividido pelo 3 elevado 2. Perfeito, galera? Todo mundo tá comigo? Daí que vem a propriedade, né? Se você for ver o que que aconteceu, eu tinha 3/ido por 4 elevado-2. Como é que ficou o resultado final?
Ficou 4 di por 3, né? Então inverteu e inverteu também o sinal do expoente. Aí que vem a propriedade, né? Quando a gente tem assim, ó, eu tenho lá ã 7/bre 8 elevado -3, as pessoas já fazem direto o quê? Inverte aqui um com o outro, fica 8/ 7 e em vez de ficar -3 aqui, fica 3. Ah, isso aqui é 8/ 7 elevado 3. Beleza? Pegou tudo demonstrado, né? Legal. Me pediram ali agora, Pedro, meu tô com uma dúvida. Se for 1 sobre 4, vamos lá. Tão me pedindo aí, eu vou fazer 1/ 4
elevado 1/ 4, né? Você nunca vai errar se você fizer um passo a passo calmo, nunca, sem se desesperar, tá? Eh, primeiro que foi uma questão ruim, né? Deixa eu fazer elevado a 1 sobre 2, por exemplo, só para dar uma resposta válida, tá bom? Então, vamos lá. Ali perguntar se é obrigatório trocar o sinal. Mas como assim, né? Não, não é querendo, é só para ajudar, justamente para ajudar, né? que cara, eu expliquei a propriedade, eu falei assim, olha, você faz desse jeito, você passa para baixo, troca o sinal, passa para cá, troc sinal,
aí você faz é obrigatório trocar o sinal. Se é só você pensar, se eu falar que não é obrigatório, eu vou est dizendo o quê? Ih, ó, dá no mesmo. Você pode pegar o 7/ 8 e dizer que é 8/ 7 e não trocar o sinal. Então, na verdade, ó, 7/ 8 elevado -3 é a mesma coisa que 8/ 7 elevado -3. Não tem, não, não tem como ser assim. Concorda? Eu expliquei justamente o procedimento é esse, né? A mesma coisa que eu fale assim, olha, 3 x 7 você faz 3 x 7 dá 21.
Aí fala assim, ó, é obrigatório fazer essa multiplicação mesmo aí que você disse, né? É a regra mesmo, né? Claro, com certeza é obrigatório, né? Eu tô mostrando aqui justamente o processo matemático para chegar na resposta. Não, se não for obrigatório, a matemática não faz mais sentido algum, tá? Eu só deixar assim, porque é porque nessa aula várias pessoas já me perguntaram coisas parecidas. Várias vezes aqui eu fiz alguma coisa e alguém perguntou assim: "Mas eh e se eu não se eu não fizer isso?" Eu falo assim: "Ué, como assim se não fizer isso, né?"
Então, olha só, 1/4 elevado 1/ 2. Primeira coisa, né? A gente bota esse expoente em todo mundo que tá na fração, né? Então aqui, ó, eu tenho 1 elevado a 1/ 2 dividido pelo 4 elevado 1/ 2, né? Eu fiz isso aqui agora. Beleza? Mas como é que eu lido com o expoente fracionário? Lembra que eu pego aqui e puxo a toalha para fora, né? Então aqui, ó, eu puxei para fora, vai ficar o qu? Olha, √ qu é claro que 1 elevado a 1 dá o próprio um, então nem vou colocar, né? Caiu aqui
os point nele. E detalhe, raiz quadrada de 1, né? Que número vezes ele próprio, duas vezes dá 1. É o próprio um, não tem diferença alguma. E aqui quando eu pegar o dois e puxar para fora, vai ficar o quê? √² 4 elevado 1. 4 elevado 1 é o próprio 4, né? Então quem é a√ quadrada 4? Qual o número vezes ele próprio? Duas vezes vai dar o 4. A√ quadrada de 4, a resposta é, deixa eu até colocar aqui do lado, né? É dois, tá? Então na verdade isso aqui dá o quê? Meio, tá?
Aí perguntaram para mim assim: "Pedro, e se fosse para vocês verem como que assim não tem erro com quando você tem essa nessa aula aqui do jeito que eu dei agora, eu acredito que realmente essa é uma aula imbatível de potenciação. Imbatível, né?" Então vamos lá. perguntaram assim, ó, Pedro, eh, deixa eu tentar escrever aqui. Ele falou assim, ó, 3/4 elevado a -3 e todo mundo entre parênteses elevado a três. Você vai ver que é muito simples, não tem erro nenhum aqui, tá bom? Então, vamos lá. Primeira coisa, né? Do jeito que você montou aí,
você botou justamente um -3 atuando somente onde? Só no três. Esse -3 aqui é de quem? Muito boa essa questão que ele colocou, hein? Muito boa, né? Não tem nada confuso. Você vai ver que é muito simples, né? Olha esse -3 aqui. Ele tá atuando onde? Esse -3 atua em quem? Me responda agora. Ele atua somente nesse três aqui. Somente. Se ele tivesse atuando esse -3 aqui em toda a fração, eu precisaria ter aqui isso aqui, que aí eu diria que esse -3 atua em toda fração. E aí vem esse três que atua em quem?
Em todo mundo que tá aqui dentro, tá? Beleza? Então no numerador, né? Esse -3 aqui, ele atua somente no numerador da fração. Concorda comigo? Eu não tô vendo ele atuar em mais ninguém. É só você ver onde é que ele tá. Esse -3 está em cima dessa base, que é o três. Por que que você acharia que ele também tá aqui no quatro? Só se tivesse mais um parêntese aqui. Aí de fato ele atua em todo mundo que tá dentro do parêntese. Tá bom? Aí então P assim, mas qual que é a primeira coisa a
fazer? Aí cara, o que você quiser, só que o que que eu já faria? Eu tentaria já resolver o de fora para dentro, né? Então, por exemplo, tá vendo esse três aqui? Ele tá dizendo que tudo que tá aqui dentro vai ser multiplicado por si próprio três vezes. Cara, eu já, você já não pode fazer aqui 3 x -3. Já não pode fazer 3 x -3, mas vai cometer um pequeno errinho. Vai cometer um pequeno errinho aqui que já vai arruinar a questão, claro, né? Porque é o que eu disse, esse três aqui ele atua
em todo mundo que tá aqui. Então é bom que você entenda o seguinte, esse três atua em todo mundo. Esse quatro aqui ele também tem um expoente que é o um. Você só não tá vendo, mas da mesma forma que esse três tem um expoente -3, né? Vou até escrever aqui, ó, mais pertinho dele, ó, né? Vou escrever aqui um pouco mais. Esse três aqui ele atua nessa estrutura inteira e esse quatro aqui está elevado a um também, tá? Então, na verdade, esse três aqui ele tem que multiplicar tanto esse expoente quanto esse expoente aqui.
Tá sacando? Então aqui, ó, o 3 da base está elevado a -9, na verdade, e o 4 está elevado a 3. Multiplicação direta, né, dispoente, porque tem ali justamente o parêntese, né? Então aqui, ó, 3 x -3 dá -9 e 3 x 1 dá 3, tá? Então grava essa resposta aqui. É claro que se eu tivesse feito da forma tradicionalíssima, que é o quê? esse três aqui, ó, vou até tirar um aqui, ó, para você ver que eu não tô inventando coisa, né? Olha só, vamos lá. O que que esse três significa? Quer dizer, olha,
todo mundo que tá sobre o meu domínio vai ter que ser multiplicado por si próprio três vezes seguidas, certo? É isso que ele significa. Vamos lá. Então, quem é que tá sobre o domínio dele? Todo parêntese. Vamos multiplicar todo o parêntese por si próprio três vezes seguidas. Então, aqui, ó, 3 elevado -3 dividido por 4 multiplicado por si próprio três vezes. Multiplicado por si próprio três vezes. Certo? Tá? Vamos lá. multiplicação de fração. A gente multiplica o numerador pelo numerador pelo numerador e o denominador pelo denominador não tem mistério nenhum, né? Então vamos lá. Como
é que a gente faz multiplicação de potências de mesma base? Eu tenho um monte de potência de base três aqui. Repete a base e somos expoentes. Então eu tenho três que eu tô devendo -3, né? Com outra dívida de -3 e com outra dívida eu tô com -9 de dívida. Eu tenho 4 x 4 x 4. Isso é a mesma coisa que dizer que eu tenho 4 elevado a 3. Então você viu aqui que 3 elevado -9/ 4, que é o que eu já tinha aqui no início, quando eu peguei simplesmente o expoentes e multipliquei
por esse expoente aqui e multipliquei por esse poente aqui. Da mesma forma que eu faria se fosse 2 elevado -4 elevado 3. Eu ia dizer que isso aqui é 2 elevado -1 de cara. Eu ia fazer 3 x -4. Eu não ia botar 2 elevado -4 x 2 elevado -4 x 2 elevado-4 para dizer que dá 2 elevado -2. Eu consigo fazer isso mais rápido, tá? Então tem que ter essa atenção de entender que esse expoente aqui também atua aqui embaixo, óbvio. Aí se eu botar esse expoente aqui um para eu visualizar, eu vou enxergar
o 3 x 1, que dá 3, e vou acertar a questão mais rápido. Beleza? Lembrem que a gente vai fazer ainda não só a lista de exercícios dessa semana, mas nas próximas semanas do ciclo, a gente vai fazer isso aqui de novo várias vezes, tá bom? Agora vamos lá. No momento que a gente tem aqui, a gente passou da primeira fase da conta, né? Então 3 x -3, né? E aí o 3 também atua nesse expoente aqui que tá aqui embaixo, fica 4 elevado 3. O que que a gente faz, né? A gente pega aqui
e fala assim: "Eu não consigo lidar com esse 3 elevado -9, né? Então eu vou passar ele para baixo." Então vai ficar assim. Olha aqui em cima sobra apenas um um para dizer, né? Que tem alguma coisa aqui. Embaixo eu tinha 4 elevado 3 e agora eu tenho 3 elevado 9. Essa é a resposta. é o um dividido por esse número imenso aqui que vai dar da multiplicação desses caras. Acabou. Vai dar um número realmente muito muito muito pequeno porque tu tá pegando um e dividido por um trambolho, tá? Beleza, Pedro? E essa mesma conta
aí que você acabou de colocar? Deixa eu ver, Pedro. E se ambos os expoentes tiverem sinais negativos, daí um resultado positivo? Perfeita pergunta. É isso mesmo. Se aqui fosse um -3, por exemplo, vamos repetir agora. Se aqui fosse -3, primeira coisa, esse -3 aqui atua em todo mundo, tá? E esse -3 é só desse cara. E esse um é só desse cara. -3 x -3 eu tenho 3 elevado menos x menos dá mais e 3 x 3 dá 9. E aqui eu tenho 4 elevado 1, só que o -3 x ele dá o quê? 4
elevado -3. Que eu tenho -3 x 1, tá? Agora o que que eu faço? Eu tenho 3 elevado a 9 aqui, não precisa descer mais, né? Claro. E aqui eu tenho 4 elevado -3. Eu vou passar o 4 para cima como 4 elevado 3. Essa é a resposta. Agora é um número imenso, imenso, imenso, imenso, né? Antes era um número pequenininho, agora é um número monstruoso, tá? Porque você mudou tudo com isso aqui. OK? perguntar ali se não tivesse o parêntese, né? Se fosse isso aqui, porém sem parênteses algum. Então, beleza, sem parêntese algum, né?
Vamos lá. Se isso aqui tá sem parêntese, eu sou obrigado a admitir, né, a visualizar e que aqui esse quatro não tem nenhum expoente nele, além do próprio um, então ele é só o próprio 4. E esse três ele tá elevado ao expoente -3, porém antes esse expoente -3 está por si só elevado a 3. Então, muita atenção aqui, tá? Eu tenho aqui ainda tudo doente, né? Vocês sabem. Então, olha só, eu tenho aqui ainda o -3, tá? Eh, eu eu botei logo três aqui porque eu quero saber quem é o expoente verdadeiro do três,
porque é um -3 que tá elevado a 3. Mas como é que é isso? Você lembra? Vamos pegar só isso aqui, beleza? Separa só isso aqui para você visualizar. Eu tenho ali um -3 elevado 3. Ó, isso aqui é só a estrutura do expoente. Bicho, você lembra que tem que fazer o 3 elevado a 3 e desprezar o sinal? Qu quer dizer botar, deixar o sinal ele de lado e só depois adicionar, porque o sinal não tá eh veja bem, esse sinal não tá elevado a expoente três. O expoente três é só do expoente, né?
Só do número ali, não do sinal. Então, eh, o 3 elevado 3 por só dá 27 e o menos permanece aqui, fica -27. Agora, essa é a resposta, tá? Beleza? OK. Show. Boa. Tá. Então, eh, e se fosse 4 elevado a, ah, tá, tá, tá, entendi. Eh, é, aí agora é isso mesmo. Agora continua aqui, né? Passa esse três aqui para baixo, né? Aí tu vai ficar aqui embaixo com 4 x 3 elevado 27. E aqui agora vai dar um número minúsculo, né? Porque é 1 dividido por tudo isso, vai ser um número minúsculo, minúsculo,
minúsculo. Beleza? OK. É isso mesmo. Aí agora ficou aqui. E se fosse elevado a uma fração negativa? Interessante. Vamos lá. Foi elevado a uma fração negativa, né? Então aqui, ó, você vai ver que sempre você vai conseguir resolver. Então, tô fazendo perguntas muito boas ali, né? Sei lá, dá um exemplo aí. A gente quer o vou botar aqui, tentar deixar até complexo, né? O 3/4. Aí o três aqui já está elevado a 2. E aí todos eles estão elevados juntos a uma fração negativa, tão elevada a - 2/3. Cara, primeira coisa que eu faria aqui,
né? Eu não eh olhando assim de fora para dentro, eu não quero lidar com esse expoente negativo. O maior problema aqui é o expoente negativo, né? que eu não tenho o que fazer com ele. Então, primeira coisa, eu vou deixar esse poente positivo. É, tem várias formas de fazer, mas assim, lembra de quando você já dominou a propriedade que você tem aquela forma mais sintética de todas, que é você só inverter o sinal desse expoente e aí na hora que você inverter você também inverte a posição de quem tá ali dentro. Você lembra disso? Então
aqui, ó, só eu vou só aqui colocar, tá vendo aqui, ó? O quatro vem para cima, ó. Esse quatro vem para cima, o 3 elevado a 2 vai para baixo, sem mudar nada deles, tá bom? E aí o expoente agora é o 2/3. Acabou. Já fiz a primeira, o primeiro golpe aqui. Esse é só o primeiro golpe. Agora, só para ninguém dizer aí que se perdeu nisso, tá? Só para ninguém dizer que se perdeu nisso. Assim, se eu pegar esse expoente aqui e distribuir agora em cada um, vai dar o mesmo resultado. Você quer ver?
Vamos lá. Eu vou distribuir esse expoente aqui em cada um. Tá vendo aqui, ó? Esse expoente aqui, ele atua tanto aqui quanto aqui, né? Então, multiplicando direto os expoentes, eu tenho aqui em cima 3 elevado a quem, ó? 2 x - 2/3. Então o 3 tá elevado ao quê? - 4/3. É isso que dá a multiplicação do 2 pelo - 2/3. Concorda? E aqui embaixo eu tenho 4 elevado quê? O 4 elevado -2/3. Porque o dele vezes o -2/3 dá isso. Concorda comigo? Deixa eu só fazer os pintos aqui um pouquinho mais bonitos, né? -
2/3, tá? E aqui - 4/3. Aí você fala assim: "Mano, eu não tenho como lidar com esses expoentes negativos, tá bom? Então, eh, pega aqui esse 4 elevado -2/3 e bota ele para cima como 4 elevado 2/3. Pega aqui esse 3 elevado - 4/3 e bota para baixo como 3 elevado a 4/3. Beleza? Você pode ter certeza que é a mesma coisa que deu aqui em cima. É a mesma coisa que deu aqui em cima. Entendeu? Como que é a mesma coisa que deu aqui em cima? Porque aqui é o seguinte, ó. Eh, tá todo
mundo ali elevado ao 2/3, né? Se você eh tirar, é porque isso aqui vai confundir a galera, né? Mas se você tirar o 2/3 daqui, ó, tirei o 2/3 daqui e botei ele aqui, e você tirar o 2/3 daqui e botar ele para fora também, para que aqui continue dando o 4/3, o que que vai ter que ter aqui que vai ser multiplicado pelo 2/3? Vai ter que ter justamente o número dois aqui ainda que a tu vai fazer 2 x 2/3 vai dar 4/3, entendeu? Então você vê que deu a mesma coisa de cima.
4/ 3 a 2 elevado 2/3. Galera, se por acaso você não entendeu isso, você só é só o seguinte, é que a aula já tá com 1 hora 16, a galera está perguntando casos extremamente avançados e aí você talvez já esteja cansado e tem que ver de novo. Beleza? Mas eu vou terminar agora a conta, tá bom? Eu só mostrei e deixa eu só tirar mais uma dúvida aqui que a galera ficou que é o seguinte, ó. A galera ficou com uma dúvida que é a seguinte: Pedro, você tava com essa fração aqui, né? Você
começou com esse desafio que fizeram para você e aí você de cara já inverteu o sinal desse poente aqui, né? E você, ó, inverteu a posição aqui da fração também, né? Então ficou aqui quatro em cima, embaixo ficou 3 elevado 2. Ó, trocou a posição da fração. E aí o expoente que era - 2/3 virou 2/3. É isso mesmo, tá certinho. É isso. Tá, Pedro, por que que você não trocou o sinal aqui? Eh, tem gente perguntando só do dois, só do três? Galera, esse sinal aqui você pode dizer que ele tá ali no 2,
-2 sobre 3e. A fração é toda negativa, tá? bicho, você trocar o sinal da fração, é isso. Você tem -2/3, agora tu tem 2/3, você já trocou o sinal da fração. Você trocou o sinal ali do numerador, você trocou o sinal da fração inteira. O sinal do numerador, ele é o sinal da fração inteira, tá bom? O único caso particular é quando você tem uma fração que tá assim, ó, - 2/3 sobre -2 sobre -3, que é isso aqui realmente menos com menos dá mais. Isso aqui é a mesma coisa que 2/3, tá bom? Mas
uma fração com sinal de negativo, ela se inverte dessa forma, tá bom? Então vamos lá. Depois que eu cheguei nesse caso aqui, cheguei nesse caso aqui agora, que que eu faço? Ué, esse expoente aqui não tá atuando em todo mundo? Sim, tá atando em todo mundo. Ã, nesse quatro aqui, que aqui só tem um, eu posso só pegar esse expoente e colocar nele, concorda? Então aqui vai ficar 4 elevado a 2/3. Mas galera, como é que eu fiz isso? Eu tive que pegar o um que tá aqui e multiplicar pelo 2/3. É que 1 x
2/3 dá 2/3, certo? E agora, né, que como não tem um aqui, às vezes a gente a gente não enxerga um, a gente pensa que assim, ó, eu coloquei o expoente aqui, mas é sempre uma multiplicação. Agora o 23 multiplicando aqui esse 2 aqui de baixo, vai ficar 3 elevado a como é que é 2 x 2/3, ó, 2 x 2/3, galera. O dois aqui só, esse 2 aqui só tá sobre 1, entendeu? Então 2 x 2/3 você vai fazer 2 x 2 4. Embaixo fica 3. Por isso que eu faço direto 2 x 2/3,
eu só faço 2 x 2 4/3. Beleza? Acabei de avançar mais um passo. Beleza? Acabei de avançar mais um passo. E agora, né? Calma aí. Por que que o 3 elevado a 2 não ficou negativo quando inverteu o 3/4 para o 4/3? Quando inverteu 3/4 para qu? Porque eu tô entendendo a pergunta de vocês. Vamos lá. A pergunta que a galera tá fazendo é a seguinte: Pedro, quando você trocou isso aqui de posição, essa é a pergunta que tá todo mundo bugado, né? Todo mundo. Tem algumas pessoas aí que estão bugadas com isso, né? Quando,
por que que quando você fez essa primeira troca aqui, essas paradas aqui não ficaram com expoente negativo, né? Você jogou para baixo o 3 elevado 2 e para cima o 4 elevado 1. E aí você inverteu esse sinal aqui, né? Ficou 2/3 aqui. E não era, Pedro, se esse 3 elevado 2 estava em cima, ele foi para baixo. Não era para ele ter ido como 3 elevado a -2 e o 1 como 3 elevado a -1, alguma coisa assim, né? Porque não, tá? Porque o expoente é o que eu falei, isso aqui é uma condensação
da propriedade anterior. Você quer que eu, vamos lá, quer que eu faça ã o passo a passo aqui da parada? Essa inversão do sinal aqui da própria parada é quando você inverte só ela de lugar. Não tá meio confuso, não. É que tem cinco, seis pessoas que não tô entendendo, mas eu acredito que ficou claro pra maioria das pessoas, mas eu vou explicar de novo, tá? É porque eu falei, a aula tá muito longa, então eu já tinha mostrado isso aqui na no outro exemplo, né? Aí eu falei assim: "Olha, você tem aqui 3/ 4",
né? Lembra disso? Tu tinha 3/ 4. Aí eu falei o seguinte, olha, no final das contas, isso aqui é o 4/3. Lembra disso? No final das contas, isso não era o 4/3 e eu troquei só o sinal dos pointes. Por que que nessa hora vocês não ficaram com essa dúvida? Lembra disso? Eu só peguei o três e o quatro, botei o quatro e o três aqui invertido e troquei o sinal só de quem tá aqui em cima, né? Para eu trocar o sinal do cara é quando eu faço passo a passo. Então, olha só, eu
tenho aqui, ó, 3 elevado, ó, eu tenho 3 sobre 4 elevado -2, certo? Vamos lá. Todo mundo aqui a gente pode dizer que tá automaticamente elevado a 1. Você concorda comigo? Sim. Então vamos lá. Eu vou pegar só, ó, ignorando aqui esse -2, eu vou pegar só esse tr aqui e vou passar ele para baixo. Ué, se eu fizer isso só com três, de fato, ele vai para baixo como 3 elevado-1. Vou pegar só esse 4 e vou passar para cima, tá bom? Ele foi como 4 - 1. E o -2? Não fiz nada com
ele ainda. Nada. Tá. Agora, o que que eu faço com esse expoente aqui? Ué, aplica ele em quem tá dentro do parêntese. Vamos lá. Para aplicar o multiplico. Então eu tenho aqui 4 elevado -1 x -2. 4 quanto é -1 x -2? 2. Menos com menos mais e 1 com 2 2. O -2 agora aplicado ao -1 aqui também. 3 elevado -1 com -2 dá o quê? 2. Agora que eu tenho 4 elevado 2/ 3 elevado 2, eu posso muito bem dizer que isso aqui é o 4 sobre 3 e aí pegar esse dois que
tá aqui, que tá aqui e escrever aqui fora. Aí você viu que na prática, o que que eu fiz? Na prática tava aqui 3 sobre 4, agora tá 4/3. E eu não mudei nada no expoente aqui. Eu não inverti os pointes aqui. Eu inverti o expoente de fora de -2 para dois. E ao invés de eu ficar fazendo nesse passo a passo é que eu já tinha mostrado isso, vocês lembram o que eu falei, como a aula vai ficando muito grande, aí o que que eu tenho aqui, ó? Ao invés de eu fazer no passo
a passo, né? Então primeira forma de fazer isso aqui, ó. 7/ 8 elevado -3. Primeira forma, aplico o -3 aqui em todo mundo. 7 elevado -3/ 8 elevado -3. Tu tá feliz com isso? Não tá. expoente negativo. Então, pega o 7 a -3 e passa para baixo, vai virar 7 a 3. Pega o 8 a -3 e passa para cima, vai virar 8 a 3. Certo? Agora que você tá olhando para isso aqui, você não pode dizer que, olha, na verdade, isso aqui é 8 sobre 7 e esses expoentes três aqui, eu posso escrever eles
aqui fora. Então, na prática, você não tinha 7 sobre 8 elevado -3 e virou 8/ 7 elevado 3? Na prática, não foi isso que aconteceu. Ou seja, eu inverto apenas o expoente de fora do parêntese. Então eu pego o -3, transformo em três e só de inverter o sinal, eu sei que eu só preciso inverter a posição do numerador e do denominador sem me preocupar com mais nada. Se tu quiser fazer daquele jeito que eu ensinei primeiro de olha, pega aqui o sete aí, primeiro aplica o expoente, aí passa ele para lá, tu pode fazer,
mas é mais lento, tá? Então, por isso agora, mais uma vez que nesse caso aqui, quando me deram esse exemplo aqui, primeira coisa, eu falei assim: "Cara, esse - 2/3 aqui eu já vou transformar ele em 2/3 e quando eu fizer isso, eu só vou pegar esse esses caras aqui e vou inverter. Vai o quatro para cima e o 3 elevado 2 vai para baixo, sem mudar nada aqui nos expoentes próprios dele, porque eu tô mudando já aqui fora. Pegou? Pegou? Não. Então, falaram aqui agora assim, nunca vi um professor explicar assim. Muita gente tá
falando isso aula inteira, por exemplo. É isso que eu falo. Eu tenho certeza absoluta. Eu não consigo pensar. Eu tenho todos os cursos do Brasil, eu não consigo pensar até hoje. Eu nunca vi uma aula desse nível aqui de pontção. Eu nunca vi, nunca. Porque essa aula aqui, além dela ter sido muito bem construída por mim, além da minha didática, eu já tô, eu já respondi aqui mais de 100 dúvidas de alunos enquanto eu dou aula. Então, cada aluno vem com uma dúvida, vem com um desafio mais avançado e eu vou respondendo. Então, não dá
para você fazer uma aula tão completa quanto essa assim, tá bom? Eh, então, ã, que que eu faço agora? É, eu tenho agora que pegar esse expoente que tá aqui fora ainda e aplicar ele em cada um aqui, né? Então vamos lá, vamos aplicar ele aqui cada um. Vamos então o 2/3 aplicado aqui nesse primeiro expoente, né? Eu tenho aqui o 4 que estaria elevado a 1, mas agora ele tá elevado ao 2/3, né? E eu tenho aqui o 3 que tá elevado a 2, mas aí aplicando aqui o 2/3 nele, ó, multiplica o 2
pelo 2/3, eu tenho 3, na verdade elevado a 4/3. Beleza? Tá? Como que eu vou agora lidar com isso? 4 elevado 2/3. Como é que eu com cada um deles eu vou lidar dessa mesma forma? Eu vou puxar o tapete aqui do denominador, ó, né? Então, puxando isso aqui para fora, eu fico com, olha, raiz cúbica de 4 elevado 2. Ó, o 2 caiu para cá e o 3 saiu. Beleza? Então, quanto que é 4 elevado 2? É 16. Então, na verdade, tenho raiz cúbica de 16. Beleza? Embaixo eu vou pegar esse 3 e puxar
para fora. Vai ficar também o quê? Cúbica de 3 elevado 4. Lembrando que 3 elevado 4 é 3 9 27 81. Então, raúbica de 81, tá? Detalhe, nesse caso aqui, eu não sei nem a raiz cúbica de 16, nem a raiz cúbica de 81. Eu não consigo saber que número vezes ele próprio três vezes dá 81. Não tem, né, um número inteiro que vezes ele próprio tr vez não, galera. Não pode e cortar as raízes. O que que você pode fazer? O que você pode fazer é o seguinte. Olha, já que é raiz cúbica 16
sobre√ cúbica de 81, você pode dizer que é raiz cúbica de 16/ 81. Você pode dizer isso? é a raiz cúbica de 16/1, mas você vai ver que também não tem nada aqui, não tem como você saber quanto que é isso, tá? Eh, vamos lá. Quer dar uma simplificada? Dá para dar uma simplificada aqui que é o quê? Vamos lá. Não sei quanto é, só porque isso poderia cair na prova, né? Ainda vou dar uma aula de radiciação, mas eu já quero adiantar aqui para eu não me sentir culpado depois. Raiz cúbica 16, eu não
sei quanto é, tá? Tenta pelo menos escrever o 16 de uma outra forma. O 16 ele é o 2 x 8, tá? Rai cúbica de 81, não sei, mas o 81 ele pode ser escrito pelo menos como 3 x 27. Vamos lá. Cúbica de 2 x 8. Cara, a raiz cúbica de 2 eu não sei, mas a de 8 eu sei. A de 8 é o próprio dois. Então eu tiro aqui a resposta, ó. Tá vendo que oito ele sai já respondido como 2. Então aqui em cima já fica 2 x √ c2. Raiz cúbica
de 3, eu não sei que número vezes ele próprio. 3 vezes vai dar 3. Agora√ cúbica de 27, eu sei, é o próprio 3. Então o 27 sai daqui de dentro e sai respondido como 3. 3 x 3 x 3 dá 27, tá? Então eu fico aqui com 3 vezes a raiz cbica de 3. Beleza? E pronto. Acaba aqui. Ou é óbvio, dá para dar uma racionalizada, tá? Mas eu vou dar outra aula de racionalização na s a gigantesca. Eu não vou agora eh não vou agora mais adicionar uma explicação aqui, porque já tá muito
densa e muito grande inclusive essa aula, beleza? Então eu acredito efetivamente, eu não esqueci nada, né? Toda toda a teoria está aqui de potenciação, né? Eu não eu não consigo lembrar de nenhuma outra propriedade, nenhuma, nenhum outro mecanismo de potenciação que poderia ser importante aqui. Deixa eu só terminar a aula botando algum desafio aqui então complexo, né? Misturando tudo aqui. Deixa eu ver aqui alguma coisa bem bem bem chata aqui pra gente fazer, sei lá. Deixa eu inventar aqui, ó. - 3 sobre 4 ã sobre 4 elevado 2. E aí o -3 tá elevado a
4. Todo mundo elevado a - 2/5, né? Legal. Ah, vamos todo mundo elevado a -1 sobre 2 para não ficar também tão tão abstrato, tá? Primeira coisa que eu faria é lidar com esse sinal aqui, tá? E para lidar com esse sinal aqui, eu só vou inverter ele. Então ele vai virar aqui 1 sobre 2, tá? E quem tá aqui dentro vai ser invertido apenas de posição, sem mudar mais nada. Então esse 4/ 2 ele vai para cima e esse -3/ 4 vai para baixo. Acabou. Primeiro golpe é esse aqui. Lar com esse -1/ 2
que virou agora 1 sobre 2. A segunda coisa aqui é aplicar esse expoente nos dois expoentes que estão aqui. Beleza? Você vai ver agora a complexidade. Olha só, o 4 elevado 2, quando eu faço 2 x, isso dá 1, né? Porque eu vou fazer 2 x 1, vai ficar 2 sobre 2, que dá 1. Então aqui eu tenho apenas o 4. Maravilha, né? Tenho só o 4 aqui, certo? Que aqui 4 2 x 1 2 2/ 2 1, tá? E agora aqui embaixo, né? Eu tenho -3 elevado 4 e isso entre parênteses tá elevado a
1 sobre 2. Ó, eu vou até fazer pausado para você não ter para você não não não perder aqui o raciocínio. Vamos lá. Esse 1 sobre 2, ele já atuou aqui em cima, então já me livrei dele. Mas aqui embaixo, galera, eu ainda tenho assim, ó, -3 sobre 4. E ele todo ainda precisa ser elevado, porque o sinal negativo foi só pro três e ele não é da fração toda. Exatamente. Ó, não, porque ele, bicho, a fração inteira é negativa, mas o sinal negativo aqui eu botei no três. Se tu mear, essa fração é positiva
ou negativa? Essa fração aí é negativa, mas o negativo tá no numerador dela. Beleza? OK. Então, agora vamos lá. Como que eu lido com esse cara aqui de baixo? O primeiro de cima aqui, ele já tá resolvido, é quatro. Só que aí para aplicar 1 sobre dois, tanto sobre esse cara quanto sobre esse cara aqui, eu fiz separadamente, entendeu? Justamente para não confundi-los. Beleza? Então, agora que eu tenho aqui esse 1 sobre do Pedro, eu posso aplicar aqui a propriedade do de puxar a toalha? Pode, pode aplicar aqui a propriedade de puxar a toalha tranquilamente,
tá bom? Só que quando você puxar a toalha, quando você jogar o dois aqui para fora desse parêntese, ele vai sair como uma raiz quadrada. E uma raiz quadrada de quem? De todo mundo que tá aqui. Ou seja, uma raiz quadrada de -3 elevado 4. Tá? E aqui que tu vai ter o problema, tá? Porque é claro que tu pode resolver o 3 elevado 4, né? Que dá 3 x 3 9 27 81. O 3 elevado 4 dá 81. Só que aqui tu tem um número negativo, tá? E não existe raiz quadrada real de um
número negativo. Não tem aqui o que fazer. Não tem o que fazer, tá? Por exemplo, que número vezes ele próprio duas vezes vai dar o -81? Me fala aí um número vez ele próprio duas vezes que vai dar o -31. Ah, Pedro 9. Não, pô. 9 x 9 dá 81. Ah, o -9, Pedro, não. O -9 x o -9 também vai dar 81, porque menos com menos dá mais. Claro que não, né? É justamente aqui você teria que entrar em números complexos. Aqui é outra matéria que não cai. Agora é justamente os matemáticos entram aí
no no conceito de números complexos, tá? Não tem o que fazer, não tem aqui o que mandar para cima, não tem aqui nenhum expoente negativo. Isso aqui não existe, tá bom? Esse exemplo que eu dei aqui acabou caindo numa coisa que não existe, tá? Não, número complexo você não vai aprender aqui no ensino médio, não vai, tá bom? Beleza. Eh, você aí é outra coisa, né? Eh, totalmente diferente. Beleza? Então, eh, essa última aqui que eu fiz, galera, ela foi bem complexa, tá bom? Pera aí. Se não tivesse o parêntese no -3, tá? Deixa eu
deixa eu fazer aqui outro exemplo. Então, pedindo assim, não faz sem o parênteses no -3, tá? Beleza. Vamos ver se assim vai funcionar, né? Se aqui é só assim, né? Então aqui, ó, tu quer só isso aqui, né? Nesse caso aqui significa que esse -2 ele atua apenas nesse 4 aqui, né? Então, na verdade, isso aqui é um -3, só que o expoente dele 4 tá multiplicado, tá? Tá elevado a esse número negativo aqui, né? Então, primeiro eu tenho aqui um expoente elevado a um número negativo aqui. Nossa, né? Isso aqui vai dar uma parada
e eu tenho que parar e fazer separado só isso aqui, entendeu? Tá vendo aqui, ó? Só o expoente dele quatro. Eu queria terminar a aula com uma coisa que deixasse vocês com autoestima, mas só estão botando aí exemplo horrível. Então, aqui, ó, o 4 está elevado ao 1 sobre 2. Tu vai ter que pensar só no 4 elevado a 1/ 2, tá bom? Ao -1/ 2. Isso aqui é muito difícil de cair na prova. e tu vai ter que pegar ele e jogar ele para baixo, tá bom? Então tu vai ter que fazer 4 elevado
1/ 2. Então esse expoente aqui elevado a esse cara dá 1 sobre 4 elevado 1/ 2. E aqui embaixo tu joga ali para fora e fica a√4. E a √4 é 2, tá? Então toda essa estrutura aqui desse expoente ela é 1 sobre 2. Beleza? Então esse 3 na verdade tá elevado a 1 sobre 2 e somente o três, não o sinal dele. Beleza? Agora tu tem ali o menos e aí o 3 elevado a 1 sobre 2, tá bom? E aí puxa aqui para fora de novo esse dois, né? Então tu tem - a√3
sobre 16, que é o 4/ 2. Beleza? E é isso. Menos a √3. A gente não tem o valor exato da√3, mas se a prova desse seria 1,71. Essa é a resposta. Se a gente se aprova falar assim: "Considere √3 como 1,7, fica - 1,7/ 16. Beleza? Sacou? É aqui é um valor real, só é um valor negativo. Tá bom? Parabéns, terminou a teoria de potenciação. Agora vai vir uma aula que é exercício, exercício, exercício varado de potenciação, tá? Então essa aula aqui que vai vir agora é bem rápida, vai pausando e fazendo, tá bom?
Porque nessa aqui eu já p pa pa pá. Não repara que quando eu coloco a letra B, eu boto aqui a resposta errada, né? Você vai perceber que assim que eu escrevo a letra B, primeiro eu coloco que era -9, depois eu volto lá e eu corrijo, tá bom? Então você vai perceber que tem esse pequeno errinho aí, porque eu tava doente no dia que eu gravei essa aula, mas eu corrijo logo em seguida. Ó, pode arrebentar que agora tu vai ver os exercícios, vai te fazer um bem absurdo. Vamos nessa, então. Eh, galera, essa
aula aqui é realmente para quem assistiu as outras teorias e tal, né? Para quem tá com a com a com tudo certinho, tá bom? Então, só para eh preencher aqui de novo, né? -3 elevado 2, o expoente aqui é par, então o resultado aqui fica nove e também fica positivo. Beleza? Então aqui a gente tem nove, aqui é só o nove e tem o menos aqui que não participa do expoente. Aqui o qu incide nos dois, né? Então fica o -1 elevado 4. Então aqui a gente tem -1 sobre 3, todo mundo elevado a 4.
Quando a gente tem aqui todo o -1 elevado 4, a gente sabe que a gente sabe que ih, e nossa, aqui eu viajei, né? Aqui é aqui é -8, foi mal, né? Tô fazendo aqui rapidinho. Eu acabei. Tenho menos aqui e aqui o oito. Desculpa aí. Então olha só, aqui a gente tem o expoente incidindo nos dois, né? Então esse -1 aqui inteiro vai ficar e 1 elevado 4 dá dá o próprio um, né? E o menos ali com um expoente par nele faz com que fique positivo, né? Então isso aqui dá 1 e o
3 elevado 4 dá 3 9 27 81. Beleza? Aqui a gente tem um menos aqui e aí dentro do parêntese tem -3/ 2 elevado 3. Então o 3 incide em todo mundo. Então esse -3 aqui elevado a 3 vai dar um expoente ímpar, né? Que é, perdão, por ser aqui um ímpar vai dar um um número negativo, né? Então vai ficar menos. E aí o 3 elevado 3 dá 27. embaixo dá o 2 elevado a 3 que dá 8. E tinha aqui um menos antes de tudo, né? Esse menos vezes menos faz ficar positivo no
final das contas, tá bom? Então a fração toda fica positiva, né? Independente a se o menos estava sólido no 27, a fração inteira fica positiva. Beleza? Eh, e aí agora só deixar aqui organizadinho. 1 sobre 81 aqui. Aqui não tem mistério, né? Aqui a gente pode encarar como 8 x 16, mas a gente pode também dizer que a resposta é 2 elevado 7, tá? Que dá 2 4 8 16 32 64 128. Aqui 8 8 el 5/ 8 e a 3 dá 8 a 2, né? A gente sobe o 8 a 3 como 8 a
- 3. Aqui a gente tem 3 elevado 6, né? Porque 2 x 3 é 6. Aqui a gente não tem como interagir essas potências diretamente nessa multiplicação porque não são bases iguais. Mas a gente pode botar aqui que isso aqui é 2 a 3 vezes no lugar do 4 eu chamo o 4 de 2 elevado 2. Só que o 4 que é o 2 elevado 2 tá elevado a 3. Então 3 x 2 é a mesma coisa que dizer que isso aqui é 2 elevado 6. Então 2 a 3 com 2 a 6 fica 2
a 9. Aqui a gente tem 16 elevado 4 dividido por 2 elevado 4. Seria interessante botar o 16 também na base 2, né? Então como é que a gente escreve o 16 na base 2? É o 2 a 4. Isso é o 16. Só que o 16 tá elevado a 4 e aqui 2 a 4 também. Então, 2 elevado 4 x 4 é 2 elevado 16. Galera, tá rápido porque eu já fiz isso aqui, já botei lá na plataforma, tá bom? 2 elevado 16 e aqui tem 2 elevado 4. Então, e passando aqui para cima
como 2 elevado -4, fica 2 elevado 12 a resposta. Beleza? OK. Perfeito. Aqui a gente tem 1 sobre 2, só que todo mundo aqui tá elevado a 2/3. Então o 2/3 ele tem que elevar os dois expoentes aqui. Vocês preferem que eu faça só para saber assim, eh, pensei nisso agora. com talvez outra cor de caneta. Será que ficaria melhor usar uma outra cor do que esse vermelho? Talvez fique melhor assim. Tá bom. Então, olha só. Tá, vamos lá. Eh, agora a partir daqui eu vou um pouquinho mais explicado, tá bom? Então, aqui, ó, 1/
2 elevado 2 2/ 2/3. Então, o 2/3 seria um expoente que tá em todo mundo, né? Então esse um aqui ele tá elevado a 2/3 e também esse dois aqui está elevado a 2/3. Como é que eu lido com o expoente fracionário? Eu pego o denominador e puxo para fora, tá bom? Então pegando aqui esse denominador 3 e puxando para fora, ele vai sair como um índice cúbico, né? Então, e aqui esse dois escorrega para baixo, tá? Só que 1 elevado 2 é o próprio um, não tem necessidade. E a raiz cúbica de 1 também
é o próprio um, né? Porque que número vezes ele próprio? 3 x dá 1 é 1. E aqui eu puxo para fora, eu fico com a raiz cúbica de 2 elevado 2, sendo que 2 elevado 2 é 4. Tá bom? Então o 2 escorregou aqui, o 3 saiu. Então a raiz cúbica de 4 eu não sei qual é, né? Então qual é o número que vez ele próprio três vezes dá o quatro? Não sei. Não tem esse número, né? Na não um número natural, tá? Seria um número bem quebradinho, né? 1.4, alguma coisa assim. Nesse
caso aqui, galera, aquela pausa de sempre, né? A gente vai fazer uma coisa que eu não ensinei ainda para vocês, tá? não ensinei ainda, que é racionalizar, tá bom? Racionalizar o quê? Quando você tem uma uma raiz eh que tá aparecendo embaixo, a gente não coloca assim, entendeu? A gente não deixa a resposta desse jeito com uma raiz embaixo, tá? E aí a técnica para racionalizar é qual? Você multiplica pela pela aquela raiz em cima e embaixo, tá? Então vamos supor que tu chegasse na prova e tu tivesse essa resposta aqui. Olha, 1 div por
√2, você não pode deixar assim. Como é que você faz sumir? Tu multiplica por √2 em cima, embaixo, ó. √2 em cima e √2 embaixo. Vamos lá. 1 x √2 dá o quê? √2. Tu não sabe quanto é, mas não tem problema. E √2 x √2, como que você multiplica a raiz? Você só multiplica o número que tá dentro dela mesmo. Então √2 x √2 é √4. Só que a √4 que 2 x 2 4. √4 tu sabe, √4 na verdade é 2. Então pronto, você racionalizou, sumiu aquele denominador que tinha uma raiz, que a
gente não gosta disso na matemática. Beleza? Tá? Como que você racionaliza aqui? Nesse caso é isso mesmo, você multiplica pela raiz em cima e embaixo. Então tua resposta é essa. O que que você vai fazer? Ah, eu vou multiplicar pela raiz cúbica de quatro em cima e embaixo. Então aqui, ó. í cúbica de 4 em cima e√ cúbica de 4 embaixo. Quanto que isso aqui vai dar? Aqui vai dar e √ cb x 1, né? √ cbica de 4. Não sei quanto é, mas não tem problema, porque o problema é ela tá aqui embaixo, né?
E aqui embaixo, quanto que dá √ cb x √ c 4? Mesma coisa, multiplica 4 x 4. Então dá √ cb 16. Eu te pergunto, tu sabe quanto é a raiz cúbica de 16? Que número que vezes ele próprio 3 vezes d 16? Eu não sei. É racionalizar só isso mesmo para quem tá perguntando. Mas ainda não dei aula de racionalização, né? Então, olha só, eu não sei qual é a raiz cúbica de 16. Que número vezes ele próprio 3 x dá 16. Não sei, pô. 2 x 2 x 2 dá 8. 3 x 3
x 3 dá 27. Aí você fala: "Então não tá racionalizado ainda por completo". Isso não tá. Sabe o que que você vai fazer? Você vai repetir. Você faz de novo a mesma racionalização. Você multiplica de novo por√ cúbica de 4 em cima e embaixo. Então tu chegou até aqui. Concorda? Ó, eu vou repetir. Você chegou até aqui, ó, √ cica 4 dividido por √ cica de 16. Você continua com o mesmo problema. Repete, multiplica de novo em cima e embaixo pela raiz cúbica de 4. Tá? Então, quanto que é√ cúbica de 4 x √ c?
Cica de 16, né? Porque 4 x 4 embaixo. Quanto que é raiz cica de 16 x √ c? Quanto que é 16 x 4? Dá raiz cúbica de 16 x 4 64. Olha que coisa boa. Você sabe quanto é a raiz cúbica de 64, tá? A raiz cúbica de 64 é 4. Que número vezes ele pior 3 x dá 64? 4 x 4 x 4 dá 64. Então aqui embaixo a gente tem a resposta que é 4. E aqui em cima continua a raiz cúbica de 16, que eu não sei quem é, mas não tem
problema. Essa é a resposta. Tem muita gente perguntando assim: "Pedro, mas não era para você fazer multiplicado e pela raiz cúbica de 4²?" Eu sei que eu falei desse método da última vez, mas esse método aqui eu, por agora eu quero que vocês façam assim, que vocês façam uma vez e depois façam outra. É a mesma coisa no fundo. É a mesma coisa. A mesma coisa, tá bom? Não tem problema. É só que esse método aqui ele é muito mais pedagógico, tá? Esse método que eu mostrei agora, ele é mais pedagógico, mais didático, mais seguro
para vocês, pelo menos por enquanto. Depois eu ensino como que vocês lidam com isso, tá bom? Essa aqui seria a resposta então da J, que como eu disse, não era para tá aqui desse jeito. Eu não queria ter botado uma questão que ia cair nisso aqui, mas eu eu acabei botando, tá bom? Então, √ cb 16/ 4 ainda dá para você dar uma mexida aqui, né, que é você falar assim: "Olha, eu não sei qual é a raiz cúbica de 16". Então eu vou escrever aqui como raiz cúbica de quem? De 2 x 8. Quem
é a raiz cúbica do 8? A do 8 eu sei. A do 8 pelo menos eu sei que é 2. Então o oito sai daqui e ele sai como a resposta dele que é 2. Então acaba que a resposta final dela é 2 √ c 2/ 4. E você ainda pode simplificar esse dois com esse 4, tá? Você pode dividir eles por dois, né? Então, divide o 2 por 2, ele dá 1, ele soma ele aqui e o 4 por 2, ele dá 2. De modo que a resposta final disso aqui mesmo é √ c
2/ 2. Beleza? E acabou. Não tem mais o que fazer aqui, tá? Não tem mais o que fazer aqui nesse caso, OK? Ã, essa aqui ficou a resposta final. Quanto é 10 elevado a 0? Qualquer número elevado a zero dá 1. Quanto é 5 elevado -2? Como é que eu lido com um expoente negativo? Você lembra? Eu preciso simplesmente jogar ele para baixo com o sinal do expoente invertido. Então isso aqui na verdade é 1 dividido por 5 elevado 2, sendo que 5 elevado 2 é 25. Então isso aqui é 1 sobre 25. Beleza? 2/5/
4.5 dividido por 4, não elevado a 4, né? O 4 afeta todo mundo aqui, tá bom? Então o 4 ele afeta o 2, que é 2 elevado 4, o 4 afeta o 5, que é 5 elevado 4. Lembrando que aqui é como se tivesse um expoente 1, né? Então a gente multiplica o 4 pelo 1 aqui nos dois casos, tá bom? Só para deixar claro, tá? Pedro, o que que eu posso fazer aqui agora, cara? Nada, você só pode resolver mesmo. Então, 2 elevado 4 = 16 e 5 elevado 4 é 5 25 125 625.
Beleza? Ótimo. Eh, e aqui 5 elevado 4, porém todo mundo elevado a 2. Eu só faço 2 x 4. Isso aqui é a mesma coisa que 5 elevado 8. Beleza? Todo mundo tá acompanhando? Tá legal assim? 5 elevado 8, né? Sem mistério aqui, tá? Eh, a mesma coisa que você pegar, ah, isso aqui tudo vezes ele próprio duas vezes, vai repetir a base e vai somar os expoentes, não tem mistério, tá? Aqui a gente tem 2 elevado 3 elevado 4. Isso aqui é 2 elevado 12. Se 2 elevado 10 é 1024, então 2,48 4,96, tá
bom? 4096. Se quisesse responder, as duas respostas estão certas, tá? Agora aqui eu tenho 5 elevado -1 vezes 5 elevado 2, porém todo mundo elevado a 3. Duas formas. Ou primeiro eu resolvo o que tá aqui dentro, né? Multiplicação de potência de mesma base, eu repito a base e soma os expoentes. Eu tenho dois, mas eu devo um, então isso aqui dá apenas um. E isso aqui continua elevado a três, tá bom? Então 3 x 1, eu tenho 5 elevado 3. Ou se eu quisesse, eu poderia distribuir o expoente aqui multiplicando os dois expoentes, né?
Então aqui, ó, o expoente aqui do 3 multiplica o -1, de modo que fica 5 elevado -3. que -1 x 3 dá isso. E aqui também fica, ó, vezes 5 elevado 2 x 3, 5 elevado 6. Quanto é você repetir a base e somar os expoentes? Tu tem seis, mas tu deve três, tu vai ficar 5 elevado 3. Beleza? E aqui 3 x 3 elevado 5 x 3 elevado -2, todo mundo dividido por 3 elevado 2. Quer, Pedro, quero pegar esse 3 a 2 e passar para cima como 3 elevado -2. Inverti o sinal dele.
Perfeito. 3 el -2 com 3 el -2 com 3 elevado 5. Vamos lá. Repete a base, que todas as bases são iguais aqui. Somos expoentes. Eu tenho cinco, mas eu devo dois e eu devo dois. Eu só tenho 3 elevado a 1, que é o próprio três. Não precisa do um aqui, OK? 8 elevado 2/3. Como eu lido com o expoente fracionário, eu pego o denominador e puxo para fora como um índice de raiz. Então o denominador vem para cá como uma raiz cúbica e o do escorrega para cá. Então eu quero a raiz cúbica
de 8 elevado 2, que é 64. Beleza? Rai cúbica de 64 é o 4. Que número que vezes ele próprio três vezes dá 64. é o próprio 4 32 elevado 5/ 5. Claro que eu posso olhar para esse 5/ 5, pegar o denominador, puxar para fora. Então eu quero na verdade a raiz quupla de 32. E esse aqui escorrega, né? 32 elevado 5. Que número, ó, raiz quinto. Que número vezes ele mesmo cinco vezes dá quem tá aqui dentro? Tá. Que número vezes ele mesmo 5 vezes dá 32 elevado 5? Claro que é o próprio
32. O 32 elevado 5 é justamente o quê? 32 x 32 x 32 x 32 x 32. Eu vou te perguntar o seguinte, que número vezes ele mesmo cinco vezes dá 32 vezes ele mesmo cinco vezes? O 32, né? Mas é óbvio que você não faria desse jeito, né? Você pegaria o 5 sobre 5 e diria: "Olha, 5 dividido por 5 é a mesma coisa que 1.". Então isso aqui é 32 elevado a 1, que é o próprio 32. Mas eu só fiz para mostrar, né, o jeito pedagógico. Tá bom? É, poderia cortar o expoente,
o índice sim também, tá? 9 elevado meio x 16 elevado a meio. Como é que eu lido com os expoentes fracionários? Eu jogo o denominador como se fosse um índice de raiz, né? Então aqui ó, o índice da raiz é 2. Fica aqui o 9 elevado apenas a 1, que é o próprio 9. Nem precisa do do aqui, né? Raiz quadrada. A gente não precisa mostrar isso. Quem é a √9? É 3. Raiz quadrada, né? Que número vezes ele próprio duas vezes dá o 9. E o 16 aqui é a mesma coisa, né? Fica a√1,
né? que eu puxei o dois para fora. Quem é a √16? É o 4. Então 3 x 4 dá 12. Beleza? Eh, então dá 12. Pedro, mostra uma outra forma interessante a fazer, tá? Uma outra forma interessante. Eu tenho 9 elevado 1/ 2 x 16 elevado 1/ 2, certo? Ã, eu vou pegar o 9 e vou escrever o 9 como sendo 3 elevado 2. Beleza? 3 elevado 2. Só que esse 9, que é o 3 elevado 2, tá elevado a meio. Vou pegar o 16 e vou escrever como 4 elevado a 2, porque isso que
ele é 4 elevado 2. Só que tudo isso está elevado a meio. Agora vamos lá. Tem aqui uma potência, né? E ela tá elevada a um expoente. Eu multiplico os expoentes diretamente, né? Então quanto que é 2 x 1/ 2? É 2/ 2 que é 1. Então 3 elevado 1, que é o próprio 3. E quanto é 4 elevado 2 x? 2 x também é o próprio 1. Então 4 elevado 1, que é o próprio 4, também dá 12 do mesmo jeito. Beleza? Só quis mostrar aí só para exercitar a mesma percepção. 27 ã elevado
a 1/3, porém tudo isso elevado a 2, né? Então eu tenho aqui 27 elevado 1/3, mas tudo isso está elevado a 2. Eu multiplico os expoentes aqui diretamente, né? Isso aqui é a mesma coisa do que 27 elevado quê? A 2/3, certo? E aí que que eu faço agora? Eu puxo esse 3 aqui para fora como um índice de raiz, tá bom? Então o três foi aqui para fora, fica o quê? raiz cúbica de 27 el 2, tá? Que número vezes ele próprio dá 20, que número vezes ele próprio três vezes dá 27 elevado 2.
Você fala: "Pô, confuso, né? Confuso. Então, ou você pode fazer 27 x 27, encontrar a resposta, né, que é 729. E aí você vai ver qual é o número que vê ele próprio três vezes dá 729, que no caso vai ser o 9, né? 9 x 9 81. 81 x 9 dá 729. Mas você também pode começar a trabalhar isso aqui, por exemplo. Como assim trabalhar, Pedro? Ó, eu quero a raiz cúbica de 27², tá? Então isso não quer dizer que eu quero a raiz cúbica de 27 x 27. É isso, né? Aí eu posso
tirar a√ cúbica do 27 x√ cbica do 27. Isso aqui é a mesma coisa que eu dizia assim, olha, eu quero a√ cúbica de 27 vezes a raiz cbica de 27. Mesma coisa. Quem é a√ cúbica de 27? é três, né? Que número vezes ele próprio 3 x d 27? 3. E quem é a raiz cúbica de 27? 3. 3 x 3= 9. Essa é a resposta. Beleza? Tá bom. Também poderia ter primeiro, né, Pedro? Eu quero escrever o 27 como sendo 3 elevado 3. É verdade, ele é 3 elevado 3. Só que ele, esse
3 elevado 3 tá elevado a 1 sobre 3 e depois tudo isso tá elevado a 2. Beleza? Tá bom? Então vamos lá. 2 vezes Então vamos lá. 2 vezes esse esse 1/3 aqui, né? Então fica ali 3 elevado 3, só que aí o 2 x 1/3 fica ali 2/3, tá? Agora 2/3 x esse 3 aqui. Então fica o 3 elevado 3 x 2/3, ó, 3 x 2 6/ 3. 6/ 3 a gente sabe que é 2, né? 6 dividido por 3 2. Então 3 elevado 2, na verdade que é 9 também do mesmo jeito. Não
sei se vocês conseguiram ver. Deu para ver? É que eu acho que ficou meio meio embaçado ali, tá? Tá vendo aqui o 27? O 27 é o 3 elevado 3, concorda? Mas esse 27 que é o 3 elevado 3, está elevado a 1/3. É verdade, né? Então vamos desenhar isso, né? Então todo 27, que é o 3 elevado 3, tá elevado a 1/3. Só que tudo isso aqui, o 27 elevado 1/3, também tá elevado a 2. Então vamos botar aqui um outro parêntese. Vamos dizer que tá tudo elevado a 2. Beleza? Tá? Tô só mostrando
várias formas de pensar, galera. É só para deixar vocês com segurança na matéria, tá bom? Então, vamos lá. Multiplicando aqui o 2 pelo 1/3, né? Expoente, elevando tudo ali ao parêntese, a gente faz dessa forma, né? Então, 2 x 1/3, você concorda que dá 2/3? Então, vou substituir aqui já. 2/3. Agora o 2/3 x o 3, quanto que dá? Faz o 3 x 2, dá 6/ 3, né? Então aqui, ó, 6/ 3, só que 6/ 3 é 2, né? Então fica 3 elevado 2 que dá 9. Deu para entender agora? Sacou? Tá. É isso. Vamos
lá. 16. Agora tava melhor a caneta azul, acho, né? Caneta azul tava melhor. Então, olha só, eu tenho aqui o 16 elevado 1/4. Ó, o 16 elevado a 1/4, porém tudo isso elevado a 3 vezes o 2 elevado a me, tá? Então eu vou multiplicar aqui, ó, os expoentes, ó, o 3 eh multiplica 1/4, fica o quê? 16 elevado 3/4 vezes, como é que eu lido com isso aqui? Eu puxo o dois para fora como sendo uma um índice de raiz, né? vai ficar 2 elevado a 1 aqui dentro e o dois vai para fora.
Então fica o quê? √2 que eu nem vou botar o dois aqui fora, né? Porque não precisa representar assim. Tá bom? Vamos seguindo. Ã, aqui eu tenho 16 elevado 3 eh elevado a a 3/4, né? Então eu posso pegar o quê? Nesse expoente aqui fracionário, eu posso pegar o denominador do 4 e puxar para fora, né? Então puxa para fora, vai ficar o quê, ó? Qu elevado 3. Concorda comigo? Aqui, ó, tinha 3/4, né? Eu puxei o quatro para fora e o três escorrega para baixo. E isso tudo aqui depois vezes essa raiz de 2.
Certo, galera? Vamos lá, pô. Qual é a o que que é uma raiz quarta? Qu é o número que vezes ele próprio quatro vezes dá aquele cara. Pior que eu conheço a√ qu só, né? Porque a√ qu é 2, né? 2 x 2 x 2 x 2 4 x dá 16. Mas do 16 eu não conheço. Que que eu faço? Eu vou separar ele, né? Então eu quero í qu de quem? √4 16 de 16 x 16. Isso aqui é a mesma coisa que 16 elevado 3, né? Depois eu multiplico pela raiz quadrada 2. Beleza?
Então vamos lá. Quem é a√ qu? 2. E a de 16? 2. E a de 16? 2. E tem aqui o √2. 2 x 2 x 2 8. E o√2 tá aqui do mesmo jeito. Acabou. multiplica o resultado isso aí. Tá bom. Estão perguntando aí, sei lá, outras fórmulas. Pedro, se eu tivesse feito primeiro ali, ã, tivesse começado já fazendo, deixa eu ver aqui que que perguntaram. Falaram assim: "Pedro, se eu tô aqui e aí eu já começo resolvendo primeiro o que tá aqui dentro, depois expoente?" Claro, pode sim, com certeza. Tá bom? Então, por
exemplo, ó, tá vendo aqui? Eu já pego e jogo esse quatro aqui para fora aqui dentro, só que sem mexer no três, né? Então fica aqui, ó, √ qu 16 e e aí o um não tem nem significância, né? Depois o 3 aqui. Aí a√ qua de 16 a gente sabe que é o quê? 2. Aí 2 elevado a 3 vai dar o quê? 8. E aí aqui tem de novo a√2, 8√2 também do mesmo jeito. Beleza? Tá, pegou, né? Ã, 2/3 elevado 2. Cara, eu acho que vai ficar melhor uma caneta menor, tá? Tô
ficando de saco cheio aqui, ó. É assim é melhor. Deixa eu experimentar também de preto. 2/3 elevado a 2, né? Então o dois afeta todo mundo, né, galera? Já vou colocar o dois aqui para atuar em todo mundo, beleza? Então vou colocar vou colocar assim, ó, 2² so 3², né? Vezes aqui, mesma coisa, né? Eu tenho 2/3, porém eu tô aqui com esse expoente três, né? Então o expoente três afeta todo mundo, beleza? OK? Agora aqui a gente tem algumas opções, né? A gente poderia resolver tudo e depois multiplicar as frações, né? Então 2 elevado
2 é 4, 3 elevado 2 é 9 x 2 elevado 3, que é 8, e 3 elevado 3, que é 27. Aí multiplica em cima, em cima, embaixo, embaixo. Ou a gente pode primeiro ver que 2 elevado 2 x 2 elevado 3 é uma multiplicação de potência de mesma base, né? Então dá 2 elevado 5. A gente repete a base somos expoentes. E 3 elevado 2 x 3 elevado 3 dá o quê? 3 elevado 5. Poderia inclusive aqui se você quisesse escrever como, né? Falar assim: "Olha, isso aqui na verdade é 2/3 elevado a 5."
Poderia tirar também, né? Total. Beleza? Poderia também repetir aqui primeiro, né? fração e somar os expoentes já nela. Perfeito. Tá? Porque no fundo mesmo, né? Eh, quando a gente tem assim, olha, 2/3 elevado a 2 x 2/3 elevado 3, isso também já é uma potência de mesma base, né? A base é o 2/3. Então, se você repetir a base e somar os expoentes, você também já tá acertando de cara, beleza? E aí é isso, tá? Dá 2/3 elevado 5. Se quiser resolver, né, você vai chegar na resposta de 2 elevado 5, que é 32, e
3 elevado 5, né, é 3 9 27 81 243. Beleza? Essa é a resposta aqui, tá bom? 4 elevado -2 x 4 elevado 6. Já sei que aqui dá 4 elevado 4, né? Dividido por 4 elevado -3. Posso pegar esse 4 a -3 e passar para cima como 4 a3? Não posso? Passa aí. Agora vamos lá. Potências de mesma base. Eu vou repetir a base que é 4 nosso expoente. 6 + 3 9 - 2 7 4 a 7. Tá bom? Pode deixar isso aqui como resposta, né? 4 a 7 é o quê? 416 64
256.000 e 64. Acho que é isso, né? 16.064. Mas nem precisa botar isso, não. Tá certo aí minha conta deve tá, né? Porque 64 deu tão certinho assim, né? Três. Agora essa daqui é traiçoeira, hein? Essa aqui é bem traiçoeira, tá bom? Cuidado. Mas se você lembrar das propriedades, não tem como você errar, né? Porque aqui os expoents, ele tem que atuar em todo mundo, né? Então, como é que os points, primeiro, isso aqui é a mesma coisa, né? Estão dizendo que deu 16.384. É isso. A outra aqui é isso mesmo. 16.000. 1384, tá? Então,
16.384. Boa, boa. É que eu falei 100 invés de 1024, né? Boa. Foi isso. Então, olha só, galera, lembra eh de distribuir aqui o expoentes, tá bom? Então, presta atenção, ó. Tá vendo aqui o o 3 elevado 2, pessoal? Para você visualizar, tá bom? Isso aqui é a mesma coisa que eu ter esse 3 elevado 2 sendo elevado a 3, beleza? Vezes, tá vendo? Esse 3 aqui ele também está sendo elevado a 3, tá? Então você faria o quê? 3 x 2 aqui é o quê? 3 elevado 6. E aqui é o quê? Aqui tem
um aqui dentro, né? Aqui é o 3 elevado 3. A resposta é 3 elevado 9, né? Multiplicando isso aqui, você repete a base somos expoentes. Tá bom? Beleza. Não, cara, poderia ter aqui também. Você poderia ter resolvido primeiro a multiplicação e depois dividido. Com certeza. Claro. Com certeza, mano. Com certeza. Tá? Estão com dúvida nisso aqui? Eu vou fazer para vocês. Vamos lá. Eu tenho aqui 4 elevado -2 x 4 elevado 6 dividido por 4 - 3. Resolve aqui em cima a primeira multiplicação. Dá o quê? 4 elevado 4. Concorda que eu tô repetindo a
base somando os expoentes. Eu tenho 6 e eu devo ficou 4. Isso tá dividido por 4 elevado -3. Tá? E aí divisão de potência de mesma base, repete a base e subtrai os expoentes. 4 - 3 dá 1. Entendeu? Não, mas aí que tá. Ah, entendi o erro de vocês. Não dá um, né? Eu falei aqui agora também comentando o mesmo erro. Eh, sabe qual o erro de vocês? É que é para repetir a base e subtrair os expoentes. Então, vamos subtrair os expoentes. Vamos lá. Subtrair os expoentes é 4 menos quem? - 3. Ó,
expoente 4 menos quem? O -3. Menos com menos dá mais, entendeu? Dá sete. Essa isso é muito traiçoeiro, muito traiçoeiro mesmo, tá? Por isso que você viu que eu faço sempre subindo. Eu não uso essa propriedade nunca. Eu acho bobeira. Não, se for uma divisão, repet. Não, eu só passo para cima. Eu sempre faço assim, tá? Mas foi uma ótima dúvida. Não, tô perguntando se não poderia subir. É claro que poderia subir. Eu tô dizendo subir para mim é mais seguro, porque eu também me confundo nisso. Por subtra poes, você vê 4 - 3, você
tira o -3, fica um. Mas tá errado, porque você subtrau uma coisa negativa é menos menos. Repete a base e subtrai os points. Esse subtrai já é uma coisa que tá aqui, é um menos que tá aqui. Aí ainda tem um outro menos que é o menos do próprio point. Pô, aí você tem que subtrair uma coisa que é negativa. Se eu tirar de você uma dívida, tu tu fica bem, tu ganha. Sacou? Aí, por isso que eu prefiro só pegar o 4 elevado, o 4 elevado -3, passar para cima como 4 a3 e aí
dá 4 a 7, tá? Prefiro assim. Beleza? Ã, aqui embaixo a a coisa que é que é trai suoira é isso, né? Você tem que se ligar, cara, que todo mundo aqui tá elevado a três, tá bom? Então, o três ele multiplica esse primeiro expoente aqui, fica 3 a 6, e multiplica esse segundo aqui que tem 1, né? Fica 3 elevado 3, tá bom? Então, repete a base soma do expoente dá 3 elevado 9. Beleza? É isso, tá? Agora vamos lá. 2 elevado -o, né? A resolução aqui ficou horrível, não sei por. Então vamos lá.
2 e ele tá elevado a -ossa, Pedro, é negativo e é fracionário ao mesmo tempo. Não tem mistério. Como é que você Eu gosto sempre de começar batendo na parte no negativo. O pior para mim é ser negativo, né? Então o que que eu faço? Isso aqui estaria dividido por um, né? Eu vou pegar esse 2 elevado -1/ 2 e vou passar para baixo. Porém, eu vou inverter o sinal do expoente. Isso, isso é o que eu expliquei na aula justamente, né? Então aqui, ó, 2 elevado -2 ele vai para baixo como apenas 2 elevado
me em cima fica só um. Então fica 1/ 2 elevado me Como que eu lido agora aqui embaixo com o expoente fracionário? Um aqui eu repito agora esse expoente fracionário aqui embaixo, como é que eu vou lidar com ele? Eu eu tiro o denominador para fora como sendo uma raiz quadrada, tá bom? Então fica ali, ó, raiz quadrada de 2, 2 elevado a 1, né? É irrelevante. Então agora eu te pergunto, como é que você vai lidar com isso? Como é que você lida com esse com esse se não muda o sinal do do? Como
assim do dois? É, toda hora vocês vocês confundem isso, né? Olha só, meu Deus. Tá, esse sinal de negativo, ele é da fração inteira. É da fração. Não importa se ele tá aqui no noador, entendeu? Não tem problema nenhum. Ele tá no numerador, mas ele, ó, vamos lá. Meu Deus, é aqui, ó, é -1 sobre 2. Isso é uma fração negativa. Isso é uma fração. Não tem como você dizer que aqui embaixo tá um positivo. Não tem, não tem, não tem, não tem. Tá bom? Isso aqui já é uma fração negativa, é -1 sobre 2,
tá bom? Você passou para baixo, você inverte esse sinal aqui, tá? Senão tu nunca, isso aqui é um número só, entendeu? É, pega o 1 sobre 2 e pensa que ele é o meio. Pronto. É, é menos meio, virou mais meio. Tá bom? Beleza. Eh, aí tão perguntando se o se o sinal da base não muda. Não, não, galera, não. Aí também é mais viajado ainda. É mais viajado ainda, porque eu nunca disse isso na minha vida, nunca. Entendeu? Perguntaram, então, perguntar assim: "Pedro, pera, vou voltar aqui naão, Pedro, mas e pera aí? E se
eu colocar uma fração que ela tem o -1 sobre -2?" Aí você ainda não simplificou a fração. Você tem que primeiro dizer menos com menos dá o quê? Mais. Então, na verdade, essa fração aqui é positiva. Não existe uma fração que fique permanentemente com sinal negativo em cima e embaixo. Quando você vê uma fração com negativo em cima e embaixo, você já vai resolver e vai dizer: "Essa fração aqui ainda não tá resolvida". Então você já vai dizer qual é o sinal dela. É o positivo. Agora sim. Agora sobre mudar o sinal da base, eu
nunca disse nada disso não, galera, de forma alguma. Mudar o sinal da base, eu se for negativo só embaixo, 1 dividido por -2. Bicho. Então é porque a fração também é negativa. Se tiver 1 dividido por -2, você pode tranquilamente dizer que isso aqui é -1 sobre 2. Você resolve diz o sinal da fração é um só. Entendeu? Eu vou ter que dar uma aula para falar disso com ainda mais calma, talvez, tá? Ah, ele pegou já. Já foi, então, né? Então vamos lá. Eh, é, se um tá negativo, todo mundo tá. Isso mesmo, tá?
Se um tá negativo, todo mundo tá. Se tem dois negativos, então você ainda não resolveu a fração. Tem dois negativos, se digitar positivo, agora sim, você resolveu a fração, tá? Vamos lá. Agora, ã, eu tenho aqui 2 elevado -1/ 2, galera. Eu passo ele para baixo e inverto sinal do expoente. Eu nunca nem toquei em dizer que inverteria o sinal da base. Isso não existe. Não existe. É falta de atenção total, tá? Cuidado com isso. Agora eu passo esse dois para cá, fica 1 di. Falta o que aqui? Racionalizar, né? Falta racionalizar. Então eu preciso
me livrar dessa raiz aqui embaixo. Qual é a técnica para racionalizar? Eu multiplico por ela em cima e embaixo. Então pego aqui, ó, multiplico por √2 em cima e √2 embaixo. Beleza? Em cima vai ficar o quê? Ah, em cima vai ficar √2. Embaixo √2 x √2. Você faz primeiro 2 x 2 vai dar o quê? √4. + √4, na verdade, é o quê? É 2. Essa é a resposta, tá? Resolveu aqui. 4 elevado -2/ 3. Caramba, eu tenho 4 elevado -2/3. Primeira coisa, preocupação aqui para mim é lidar com esse expoente negativo. Esse é
o primeiro problema que eu enfrento aqui, tá? Eh, presta atenção aqui na aula, mano. Você tá perguntando aí um monte de coisa para mim. Ô, Gustavo, se concentra aqui, cara. Pô, para de perguntar outras coisas e concentra no que eu tô falando, tá? Entendeu? Pelo amor de Deus, tá? Então, olha só, 4 elevado - 2/3. Primeira coisa é eu inverter isso aqui, jogar lá para baixo e mudar o sinal do expoentes, tá? Então vai ficar 1 di 4 que tá elevado aqui em 2/3. Então inverti o sinal dele aqui agora. Perfeito. Tá? Agora esse um
aqui em cima não tem muito o que fazer com ele, tá? E aqui embaixo, que que eu faço com isso aqui? Eu pego o três e jogo aqui para fora, tipo como um índice de raiz. Aí, velho, se eu não estiver ocupado, quando puder, bota um café para passar. Assim aqui, ó. Jogo o três aqui para fora, fica uma raiz cúbica de 4 elevado 2 + 4 elevado 2 é o quê? É o 16, tá? E aí, você sabe, né? Você sabe qual é a primeira coisa? Você sabe a raiz cúbica é 16? Eu não
sei quem é o número que vez ele próprio três vezes dá o 16. Não tem nenhum número exato que faça isso, nenhum número eh inteiro, né? Tá. E tá, que que eu faço agora? Então, Pedro, racionalizo. É, racionaliza. Tem uma raiz embaixo, né? Isso é uma coisa incômoda, não pode ficar assim. Como eu disse, ainda vai ter uma aula bem completa de racionalização, mas eu já expliquei para vocês, né? Você olha para esse cara aqui embaixo que é o o raiz cúbica 16, você fala assim: "Vou multiplicar em cima e embaixo por ele. Vou multiplicar
em cima e embaixo pela raiz cúbica de 16 para ver se ele some, né? E aí, será que vai sumir agora?" Vamos lá. Em cima ficou o quê? √ cb 16. Embaixo cbica de 16 x 16, né? Então, raiz cúbica de 16², podemos dizer assim, né? Será que já tem raiz cúbica para isso aqui, né? 16² é a mesma coisa que que cada 16 é um 2 elevado a 4, né? Então é 2 elevado 8, né? Então isso aqui já é o 256. O 16² é isso. 256. Temos a raiz cúbica de 256. Ã número
vezes ele mesmo? Três vezes dá isso? 4 x 4 não é de cabeça assim não, né? Poderia tentar dar uma simplificada aqui, talvez. É, só tô vendo aqui se eu vou conseguir achar isso de cabeça. Não tem não. Não tem. Então o que que eu vou fazer, galera? Eu vou racionalizar mais. Eu não consegui resolver o problema. Eu vou fazer o que eu vou multiplicar de novo em cima e embaixo de novo, por raiz cúbica de 16. Raiz cúbica de 16. Olha agora √ cbica de 16 x √ c 16. Fiquei aqui com raiz cbica
de 16², né? Porque 16 x 16 é 16², tá? Agora√ cbica de 16² x 16. Aqui eu não tenho 16² e aqui eu tenho vezes 16. Isso vai ficar 16³, né? Olha que interessante. Raiz cúbica de 16³. Isso é muito bom para mim, né? Porque olha a pergunta, que número vezes ele mesmo três vezes dá o 16 elevado 3,? Sendo que o 16 elevado 3 é justamente 16 x 16 x 16. Ou seja, o número que vezes ele mesmo três vezes dá 16 elevado 3 é 16. Quando você vê que aqui tá com o mesmo
índice que aqui tá o expoente, você pode cortar um com o outro também, tá bom? Se facilitar para você. Então aqui embaixo fica apenas 16 e em cima fica a raiz cúbica de 16². Beleza? Pronto, tá resolvido. Sim, tá resolvido. Não tem mais o problema de ter uma raiz embaixo. Quer dar uma simplificada, por exemplo? Vamos dar uma simplificada. Vamos. Então, vamos lá. Eu tenho aqui, olha, raiz cúbica, deixa eu fazer aqui grandão, ó. Raiz cúbica. de 16 quad sobre 16, tá? Ã, 16² eu posso escrever como sendo 16 x 16, sendo que cada 16
ele é 2 x 8, né? Então eu vou escrever aqui, olha só, 2 x 8 x 2 x 8 é a mesma coisa que tava escrito antes, né? 16². Eu sei a raiz cúbica desses 8 aqui, né? Porque √ cb 8 é 2. 2 x 2 x 2 dá 8, né? Então aqui, ó, tá vendo esses oito aqui, ó? Os dois saem aqui para fora como dois. vezes 2, entendeu? Sacou? Perguntaram, não poderia ser 4 trocar o 16 por 4 x 4? Sim, mas você sabe a raiz cúbica do 4? Não, eu sei do oito,
tá? Então você entendeu o que eu fiz, ó? Eu abri o 16 em 2 x 8 x 2 x 8. Aí o 8 eu sei a raiz cúbica, eu tirei a resposta do 8 aqui como 2. E desse 8 também tirei. Então aqui já vai ficar 2 x 2, né? Aqui fora fica o quê? 4. Tá? Então já resumindo aqui, ó, fica 4 vezes a raiz cúbica de quem? 2 x 2, né? Cúbica de 4 sobre 16. Eu ainda posso pegar esse 4 e esse 16 e dividir cada um deles por 4, tá? Então, dividiu
aqui por 4 fica 1 e dividiu aqui por 4 fica 4. De modo que sobrou, na verdade apenas o quê? Rai cúbica de 4 sobre 4. Essa é a resposta mais simplificada que existe. Beleza? OK. Show. Pronto. Vamos pra próxima, tá? Olha essa próxima aqui, que coisa linda, né? Primeiro, eu tenho aqui um -3, tá? Ele está elevado a 2, beleza? Né? Lembrando que aqui tem um também. Se quiser eu posso ã, né? Mas o grande problema aqui, na verdade, é o sinal, né? Então eu preciso ter atenção aqui com o sinal antes de fazer
isso, tá? Porque o dois ele afeta não apenas esse cara, mas ele afeta o sinal também, tá bom? E aí, além disso, todo mundo está elevado a cinco, tá? Então, primeiro eu posso sim, né, fazer aqui justamente o 5 vezes o 2, né? Então 5 x 2 aqui dá quanto? Primeira coisa, eu continuo tendo ali o meu -3, que tá totalmente elevado a esse dois. Só que tudo isso aqui tá elevado a 5. Então eu vou pegar já o 5 x 2 aqui e vou dizer: "Olha, o meu -3 tá totalmente elevado a 10". Beleza?
Tá? Lembra da propriedade? Tá todo mundo dentro do parênteses, inclusive o sinal de menos, né? Então, nesse caso, eu já tenho que saber dizer o quê? Olha, cara, eu sei que isso aqui vai dar 3 elevado 10, mas o sinal disso aqui, o sinal disso aqui mesmo vai ser quanto? O sinal, por ser aqui um um expoente par, vai ter que ser um sinal positivo, tá? Então a resposta aqui vai dar um número positivo. E que número positivo é esse? É o 3 elevado a 10, tá bom? Positivo, tá? Quem é o 3 elevado a
10? Aí tem que fazer aí 3 x 3 x 3 x 3 x 3 10 vezes, tá bom? Vou deixar só assim mesmo, né? 3 elevado 10 positivo. Essa é a resposta, tá bom? OK. Vamos mais. Agora começam aqui mais questões, né? Tem duas letra B aqui, né? Outra letra B agora. Vamos lá. Bora. Ã -3. Só que todo o -3 está não tem aqui o -3 elevado 2, né? Então tem primeiro aqui o -3 elevado 2. Só que tudo isso está elevado a 5. Beleza, Pedro? Eu poderia resolver primeiro dentro do parêntese porque, Pedro,
eu acho que esse dois aqui só tá incidindo no três e não no menos. É verdade. Então você pode aqui dentro repetir o menos e dizer que 3 elevado 2 é 9, sem problema algum. Só que tu tem que lembrar que tudo isso, inclusive o sinal e essa estrutura aqui que tu já chamou de nove, tá elevado a c. Beleza? Então agora você tem ali uma potência de base negativa toda no parêntese elevado ao expoente ímpar. Então isso tem que dar um sinal negativo. Tem que dar um sinal negativo. E aí o número é o
quê? É o 9 vezes ele mesmo cinco vezes. Tá bom? Então vai dar um número negativo. E aí é o 9 elevado 5. Só que agora negativo. Você entendeu a diferença de tirar ele daqui e colocar para lá? Antes eu tinha, olha o -9 elevado 5. Agora eu só tô com 9 elevado 5. Só o 9 elevado 5. Por quê? Porque eu já sei que o sinal vai ficar negativo. Então você entende que o cinco ele já atuou no sinal, por isso que ele não precisa mais atuar. O cinco já atuou no sinal e isso
ficou menos vezes menos vezes menos vezes menos vezes menos. Então menos com menos mais menos menos mais menos. E já botei aqui a resposta. Deixei só ali o número agora. Tá entendido? Assim, sacou? Beleza, Pedro. Poderia ter multiplicado aqui o o C pelo pelo do poderia, né? Ia ficar menos 3. Claro que poderia. Aqui, ó. Então aqui eu pego aqui o 5/ 2. Poderia ficar -3 elevado a 10, tá? Que é a mesma coisa que tá aqui, né? É o -3 elevado 10. Beleza? Aí você fala assim: "Mas como que é a mesma coisa que
tá ali, cara? Olha só. Troca esse nove aqui. Só troca esse nove aqui pelo 3 elevado 2, que é o que ele é. Então tem ali um tem aqui o 9, que é um 3 elevado 2, e somente o 9 está elevado ao 5. Só o 9, tá? Só o nove. E aí eu tenho aqui um sinal de menos e aqui eu tenho o 3 elevado 2 x 5 10. Mesma coisa de antes, sacou? Pegou, tá? Então vamos lá. Agora essa aqui, né? Eu tenho aqui, ó, o -2, só que esse -2 está elevado a
4, né? A gente sabe que a base é negativa, o expoente é par. Então, o sinal disso aqui no final das contas precisa ser um sinal positivo, beleza? Precisa ser um sinal ã positivo. Galera, dá, tem muita pergunta chegando. Se concentrem mais na aula, vocês estão me distraindo, tá? Muita pergunta mesmo. Eu vou desligar o chat aqui, não vou mais responder pergunta nenhuma, porque é muita pergunta, tá? E principalmente tem gente que manda a mesma pergunta várias vezes. Eu vejo todas as perguntas se eu não não respondia porque eu não quero responder, entendeu? E não
é porque eu eu tô de má vontade, é porque eu acho que não vai ser pertinente agora, entendeu? Então, se se eu imagina, bicho, eu dou aula para centenas de pessoas ao mesmo tempo. Pode parecer que é ah, você não vai responder, mas na verdade é egoísmo com os outros se eu parar a aula para responder todo tipo de dúvida, sacou? Então, olha só, -2 aqui elevado a 4 vezes o -2 elevado 3. Cara, não tem mistério aqui, né? É você saber, olha, potência de base negativa com o expoente par, isso tem que dar positivo,
tá? Então isso aqui, na verdade, vai ser, ó, 2 elevado 4. Já resolvido o sinal. que vai ser positivo. E aqui potência de base negativa elevado a um expoente ímpar tem que ser negativo, tá? Então isso aqui vai ser um número negativo no final e o 2 elevado a 3, né? Posso colocar assim o -2 elevado 3. Você percebe a diferença? Eu só quero ver se vocês estão entendendo a sutileza que eu fiz daqui para cá. Eu tô resolvendo, você entende? Eu tô resolvendo porque antes o expoente ainda ia atuar no sinal e no número.
E agora eu já tô dizendo que o expoente já atuou no sinal, então ele só precisa agora atuar no número. É sofisticado, né? escrever assim: "Eu quero que vocês peguem essa manha". Entende? Então ficou aqui 2 elevado 4. Agora aqui, ó, agora eu não me preocupo mais com isso. Eu só boto aqui o sinal, né? Eu tô botando parêntese só para não confundir. E aí o 2 elevado 3 dá 8. Beleza? Então quanto que é? Eh, agora é que óbvio, né? Teria valido mais a pena eu manter desse jeito aqui mesmo, né? E fazer a
multiplicação. Então tenho 2 elevado 4 vezes aí vamos lá. Vezes um número negativo. Vai dar negativo no final das contas, né? 2 elevado 4 vezes, então aqui tem + 2 elevado 4 x 1 -2 el 3, tá? Agora, eh, multiplicação de potência de mesma base, isso aqui dá 2 elevado 7, só que negativo, tá bom? Eu somei, vocês viram 2 elevado 4 com 2 elevado 3, somei, deu 2 a 7. E como tem só um negativo na multiplicação, mais com menos dá menos, tá bom? Ã, 2 elevado 4 x 2 elevado -3. Beleza? Pera aí.
Poderia explicar a segunda passagem? Não entendi. O que que está com dúvida? Qual foi a sua dúvida aqui? Vamos lá. Aqui, ó, eu tenho -2 elevado 4. É uma potência de base negativa num expoente par. Vai ter que dar um resultado positivo, concorda? E 2 elevado 4. Eu poderia botar resposta, né? Mas eu prefiro botar assim, 2 elevado 4 só, tá? Para poder fazer a multiplicação de potência de mesma base. Agora eu tenho aqui, olha só, -2 elevado 3. Você já não sabe que por ser uma potência de base negativa elevada a um expoente ímpar,
isso tem que dar um número negativo? Concorda comigo? Então tem que dar um número negativo. E aí, que número é esse? É o 2 elevado a 3. Agora, né? Eh, mais vezes menos dá menos e 2 a 4 x 2 a 3 dá 2, tá? 2 à4 x 2 elevado -3. Ué, repete a base. Somos expoentes. Eu tenho 4 com -3 dá 2. É porque o 4 com -3 eu sei que vai dar 1, né? E aí o 1 eu já boto que vai dar 2 na resposta, tá? - 2. Só que todo mundo elevado
a 4, né? Antes estava assim também. Antes estava assim também. -2 todo mundo elevado a 4. Só que agora ao invés de ser um -2 elevado 3, é vezes um 2 que tá elevado a 3. Beleza? x 1 2 que tá elevado a -3, né? Então tá, primeiro vou resolver isso aqui, né? Porque esse 4 ele tá incidindo tanto sobre o sinal quanto sobre o número, né? Então, por ser uma potência de base negativa elevado a um expoente par, o sinal final vai ter que ser uma coisa positiva, né? E vai ser que coisa positiva?
Vai ser o 2 elevado a 4 positivo, tá? Vezes, tudo bem? Beleza, vai lá. Vezes 2 elevado -3. Tá bom? Então aqui eu tenho multiplicação de dois números positivos, vai dar positivo. Repito a base e somos expoentes. 4 com -3 dá o quê? Dá 1 de novo, né? Então 2 elevado 1 é igual a 2. Mesma resposta. Beleza? Todo mundo acompanhando? Vamos mais. 2 elevado 4 vezes agora 1 - 2 que tá elevado a -3. Beleza? É, tão diferentes mesmo, né? Tá diferente, né? Sim, tá diferente. Então aqui agora todo -2 tá elevado ao -3,
tá bom? Então aqui, ó, vezes 1 -2 que todo ele está elevado a -3. Primeira coisa, uma potência de base negativa, el Opa, isso vai olhar, pera aí, pera aí, pera aí, pera aí, né? Eu já tenho um problema maior que é esse expoente negativo, né? Como eu vou lidar com ele, né? Ó, tá vendo o 2 a 4? Repete ele. A invés de tu multiplicar o 2 a 4 por esse -2 elevado -3, tu pega todo esse -2 que tá elevado a -3 e joga para baixo. Lembra essa estrutura inteira aqui do -2? Ela
continua aqui agora sem mudar nada nela. O que muda é o sinal do expoente que agora vai ser -3 a 3. Acabou. Agora tu resolve, né? 2 elevado 4. Deixa aqui. E aqui embaixo tu tem uma potência de base negativa, só que ela tá elevado a um expoente ímpar. Então o sinal final tem que ser negativo. E qual é o número que vai est aqui? O sinal eu sei que é negativo, né? O três atuando no menos. Menos vezes menos mais vezes menos negativo. E o três atuando no 2. Eu sei que dá oito, mas
eu quero botar só 2 elevado a tr mesmo. Agora, né? Eh, e aí agora o que vocês estavam com dúvida agora, hein? Vamos lá. Isso aqui é uma fração e essa fração tem aqui um numerador que não tem nada nele e um denominador que tá com sinal de negativo, galera. Isso aqui é você dizer que a, ó, essa fração tem aqui em cima mais. Ela não tá resolvida ainda. Ela tem um mais aqui com menos. O que que isso dá? Menos. A resposta da fração é menos. Acabou. Entendeu? Você vai bater os sinais dela. Ela
tem mais em cima e menos em baixo. Você vai já vai dizer: "Tá, isso aí é uma fração o quê? A resposta da fração agora, independente se é numerador da fração, é isso, é menos, é uma fração negativa, tá? Agora sim, era uma fração negativa. E tem aqui o 2 e elevado a 4 dividido pelo 2 elevado a 3. Fala: "Pedro, mas pera aí, não entendi. Você passou o menos estava aqui em cima." É isso aí. Eu tô resolvendo o sinal da fração. Que diferença faz? Se eu tiver assim, olha só, ó, eu tenho 3
vezes o o -2. Quanto que dá isso? Você não vai fazer assim, ó. Mais com menos. Menos 3 x 2 - 6. Aí eu te pergunto, teria tido o problema se antes eu falasse assim, olha, não, na verdade eu tenho -3 x 2, nenhum problema. Ia dar -6 da mesma forma, sacou? Então assim, a fração aqui ela tá ainda na meio que prévia, né? Ela não foi resolvida ainda. Quando você disser qual é o valor final que vai dar, você vai falar: "Tem mais aqui, um menos aqui, então é menos". Se tivesse um menos em
cima e um menos em baixo, você vai falar: "Então é mais". Tá? E agora é isso. Você tem aqui o 2 elevado 4 dividido pelo 2 elevado 3. Tá bom? Não é dividido pelo -2 elevado 3, não, né? Você eh tem aqui embaixo ele ele tava aqui com -2 elevado 3. Você pode dizer que a fração é toda negativa, tá? E não se importar mais com isso. A fração é toda negativa. Independente de onde eu boto o sinal de menos. Se quiser deixar aqui embaixo, pode deixar também, não vai fazer diferença nenhuma, tá? Não tem
problema algum. Eh, pô, se Ah, não, Pedro, eu quero deixar ele lá embaixo. Tá bom, então. Pronto, age normalmente. Quanto é dois? qu dividido por 2 a 3. Só que aí para isso, né, você vai ter que ficar assim, ó. Vou manter um mais aqui em cima e um menos aqui embaixo. Aí o 2 à qu tá aqui. Aí só esse 2 a3 vai passar para cima, vai passar como 2 a -3, né? Porque vai inverter o sinal. Aí isso aqui daí vai ficar o quê? O negativo aqui embaixo. Não faz sentido, entendeu? Você vai
dizer que o negativo é da fração toda, tá? Você já vai falar mais com menos dá o quê? Menos. 2 em cima, tá aqui. E aí sobe um 2 elevado 3. Sobe como 2 elevado -3. Qu é que é isso aqui, né? Primeiro que eu tenho um sinal de negativo aqui que vai prevalecer, né? Porque aqui tem menos, aqui tem mais, vai ficar menos. 2 elevado 4 com 2 elevado 3 repete a base e somos os expoentes, dá o quê? 1. Então -2 no no total - 2 elevado 1, né? Só que 2 elevado a
1 é o quê? 2 elevado 1 é justamente 2. Pegaram? Pegou? Agora você vê, você realmente acha, cara, que, pô, é muito, muito, muito improvável que mais do que 1% dos concorrentes consiga fazer essa lista aqui toda sem errar nada pelo nível de detalhamento das questões, tá? Tô falando sério, mesmo quem é de alto desempenho, tá? Isso aqui não é fácil não. Então, se você se você for ver essa lista, não é fácil, cara. Se você pega essa lista aqui, tô falando pega essa lista aqui e passa paraas pessoas que você conhece, senta com as
pessoas que você conhece, fala assim: "Faz esse exercício aqui agora para ver se você acha a resposta". faz esse experimento. Você vai ver que mesmo as pessoas que você pensa que são boas não vão conseguir fazer tudo sem errar. Se conseguir é porque o cara realmente é muito bom, tá? Vamos lá agora, tá? Então, primeira coisa, né? Expoente negativo, né? Olha, eu botei meu professor para fazer, ele não sabia como fazer. Bizarro. Aí é bizarro, né? O professor não sabe aí é sinistro. Então, olha só, vamos lá. Primeiro problema aqui, né? Primeiro eu tenho uma
série de de tem isso aqui menos isso aqui e mais isso aqui. Então isso aqui é uma soma de frações. Mas antes de eu me preocupar em fazer soma e subtração de frações, é claro que eu preciso lidar com esses expoentes, né? Eu preciso resolver tudo e deixar tudo tudo assim como fração simples para eu somar e subtrair. Então vamos resolver esse primeiro cara aqui. Ele é o 2/3 elevado -2, né? Eh, falou que o professor, moleque falou: "Meu professor caiu naquela pegadinha do 4 elevado 7". Ele tava dizendo que era 4 elevado 1, né?
Que era repete a base, subtra alguma coisa assim, né? É isso. Eh, é fogo, bicho. Tá ali. Meu tio engenheiro também não soube não. Aí, daqui a pouco agora vai começar as piatras. A galera vai falar: "Ah, pedi para mestre de obras, ele não soube, vamos lá". Lembra da técnica que eu te passei? Lembra da técnica que eu passei na aula teórica? Como é que você lida com isso aqui? Você livremente vai vir aqui e vai dizer que esse expoente, na verdade, é o dois. inverti o sinal de É. E aí aqui dentro tu também
troca só a ordem sem mudar sinal de ninguém, tá? É óbvio, né? Quer fazer aí do jeito complicado. Vamos lá. Distribui o dois aqui dentro. Então vai ficar 2 elevado -2. E o 3 aqui, ó, o -2 também é expoente dele, né? Então 3 elevado -2. Agora tu pega esse 2 elevado -2, passa ele aqui para baixo, beleza? Ele vai para baixo e vai inverter quem? o sinal do seu expoente. Então vai ficar 2 elevado a 2. Pronto. Esse 3 elevado -2 tu joga para cima, vai ficar 3 elevado a 2. Aí agora que tu
fez isso, tu tem 3 elevado a 2, né? Só vou trazer aqui mais pro centro dividido por 2 elevado a 2. Aí se tu quiser, tu pode falar assim, ó. Já que os dois estão elevados a dois, eu vou tirar o dois daqui e vou botar aqui fora. Aí fica 3/ 2 elevado a 2. É a mesma coisa que eu tinha feito, só que eu fiz direto, né? Então aqui, ó, tu só vai pegar esses caras aqui, vai inverter, ó. Na verdade, isso aqui é o 3/ 2 e não tá elevado a -2, tá elevado
a 2. Todo mundo entendeu isso agora? Todo mundo entendeu isso agora? Tá. Vamos lá, Pedro. Posso já botar o dois aqui agora em cada um deles e dizer que é 3 elevado 2 sobre 2 elevado 2, que é 9 sobre 4. Pode, quer fazer, faz. Tá? Então aqui, ó, o 2 atua aqui, fica 3 elevado 2 e o 2 atua aqui, fica 2 elevado 2, né? Então a gente tem aqui 9 sobre 4. Beleza? Então a primeira fração já tá totalmente simplificada, tá? Menos quem? Já botei o menos aqui. Agora vamos lidar com esse cara
aqui sem o menos. Percebeu? Meio que eu já botei o menos aqui. Agora que eu botei o menos aqui, eu vou me preocupar só com ele aqui. E o sinal de menos vai tá lá esperando. Muito bom, né? Perfeito. Né? Senão tu vai falar: "Nossa, isso aqui é o menos, sei lá, pô. Porque esse -1 aqui não tá atuando nesse sinal aqui. Então não é uma preocupação minha. Eu posso literalmente só deixar o sinal aqui em standby e lidar só com que o meu desafio. Meu desafio é esse 1 sobre 2 elevado-1. Beleza? Só que,
cara, não é um desafio de verdade, porque se tu inverter o sinal desse expoente aqui, ele vai ficar o quê? Um. Concorda? Invertiu o sinal, ficou um. E aí tu inverte a posição aqui também, fica 2 sobre 1. Primeiro que é a mesma coisa do que 2, né? 2 dividido por 1 é 2. E aí 2 elevado 1 também é o próprio 2. Então acabou. Isso aqui tudo virou menos. Aí quem isso aqui tudo é do meio elevado -1, na verdade é 2. Você viu? Bacana, né? As propriedades vão virando uma arma poderosíssima. Você nunca
mais vai ter problema com isso na sua vida. Esse mais aqui, cara, eu vou deixar ele aqui em standby, tá? Mas o quê? Aí agora, olha a diferença. Aqui tem um menos 1/4 e todo mundo aqui tá na incidência do -2. Então, pera aí, né? Primeira coisa, eu quero tirar esse -2 e transformar ele em dois. Beleza? Então a fração era o quê? Era -1/ 4. Agora ela vai ser -4/ 1. Eu só inverto a posição do numerador e do denominador. Passei isso aqui para cima e isso aqui para baixo, tá? E ao invés dela
tá elevada a -2, ela tá elevada a 2. Beleza? Pegou? Tá. E agora, Pedro? Não era melhor resolver isso aqui mais um pouco? É. Beleza. Então vamos botar o dois para incidir aqui dentro em todo mundo. Só que ele tem que incidir também no sinal, tá? E eu não sei se você lembra, mas uma potência de base negativa, cara, isso aqui é um número negativo, né? Não tem estresse nenhum com isso aqui. Isso aqui eu sei que 4 sobre 1 é só o qu, mas cara, independente de mesmo que fosse 4 sobre 3, qualquer coisa
assim, você tem que só eh e e faz a potência do sinal separada. Ó, eu vou começar a reescrever tudo de forma organizada, beleza? Tá vendo ali o 9 sobre 4? Tá aqui. Menos 2 mais. Agora vamos lá. Eu quero que você bote só, faz a potência do sinal. Por exemplo, a potência de um sinal negativo ao quadrado é o quê? É mais, entendeu? É mais. Tem gente que falou: "Não, o dois não mexe no sinal." Mexe exatamente, ele mexe no sinal agora. Sim, agora ele mexe. Só quando eu troquei ele de -2 para 2,
ele não mexeu no sinal. Mas agora quando eu vou incidir ele, quando eu vou atuar ele, você tem que entender que isso aqui é um é um menos que tá ao quadrado. Então menos vezes menos vai dar o quê? Mais. Então aqui tá vendo no dois aí tem esse mais aqui. Agora adivinha vai ter outro mais. Ou seja, não vai mudar nada. Esse menos aqui vai virar um mais. Então, mais com mais não muda nada. Ou seja, eu vou deixar só esse mais aqui mesmo. Você entendeu? Agora o mais é, pode botar mais, mais, mais,
mais, mais vezes mais, nunca vai mudar nada. Vai ser sempre mais, só o menos é que tem poder de inverter, entendeu? Lembrando que se aqui fosse um expoente três, aí sim o três atuando no negativo já é menos com menos, mais com menos. Aí ia ser o quê? Menos. Aí mais com menos ia prevalecer o menos. Mas é que não é o caso, é que não é um três, é um do Aí, entendeu? É isso. É, é aquela regra do, olha, uma potência de base negativa com expoente par o número final, o o a o
sinal final vai ser positivo, tá bom? Porque o sinal aqui tá dentro do parênteses, ele tem que tomar a incidência da potência. Agora vamos lá. Agora eu tô livre. Eu já sei que aqui tinha um mais. Esse aqui vai virar o mais. Não vai fazer diferença. Agora eu tô livre para usar o dois, para incidir o dois no quatro, né, que vai dar o quê? 16. E para incidir o dois no um, que vai dar o próprio um. Então não vai fazer diferença nenhuma. Vou deixar só assim, tá bom? Essa é a expressão final que
eu tenho que resolver, tá? Então eu tenho 9/4, tenho 9/4 e quero tirar dois dele. Só que vamos lá já colocar. Eu quero tirar dois, só que esse dois tá o quê? Sobre 1. E quero somar 16, só que esse 16 tá o quê? Sobre 1. Por que que eu fiz isso? Porque eu tenho aqui uma fração, né? Então, eh, melhor forma de eu somar a fração é isso. Bota todo mundo dividido por um, tá? Que denominador eu quero aqui? Eu quero que os denominadores virem quatro. Você concorda comigo? Eu desejo que os denominadores virem
quatro. Então, como é que eu faço para esse denominador aqui virar quatro? eu multiplico ele por 4 e aí em cima eu também multiplico por 4, fica o quê? 8. Lembra que eu tinha o -2 aqui? Agora eu tenho -8 sobre 4. Ainda é 2, né? 8/ 4 é 2. Agora eu tenho 16/ 1. Como é que eu faço para isso aqui virar 4? Multiplico por 4. E em cima também eu faço o quê? Multiplico por 4, que dá 64. Eu tinha 16, agora eu tenho 64/ 4, continuo tendo 16. Agora, como é que eu
faço operação aqui com frações que t o mesmo denominador? Eu apenas repito o denominador e executo a adição e a subtração que eu quero. Então eu tenho 9 - 8, isso dá 1, né? 9 - 8 dá 1. Agora eu tenho 1 + 64. 65/ 4. Não tem mais o que simplificar aqui. Essa é a resposta. Isso é muito importante, tá? Isso é muito importante. A gente tá em novembro, a gente tá tendo essa vantagem, né, de poder cuidar desse assunto aqui com toda a calma do mundo. Quem entrar na plataforma em janeiro, fevereiro, março,
abril, vai ter que cuidar disso aqui do mesmo jeito. Só que, né, tem cada a vocês estão cuidando com muita antecedência, tá bom? Você que tá assistindo aí agora, dê muita atenção para isso aqui, independente do tempo que você esteja, tá bom? Ah, blá blá blá blá blá blá, não interessa. Elevado a zero é um. Qualquer número do mundo elevado a zero é 1, não é verdade? Então, a 2 15 não interessa. Ele a 0 é 1. 1 x 3 elevado -2. Como é que eu lido com esse 3 elevado -2? Eu passo ele lá
para baixo como 3 elevado a 2. Acabou. Isso aqui é 1 di elevado 2, sendo que 3 elev 2 é 9, é 1.9. Beleza? Também poderia ter dado a resposta aqui em cima em número. Isso mesmo. 9/ 4 é 2,25 - 2 dá 0,25 com 16 dá 16,25. É isso mesmo. Se você dividir o 65 por 4 também dá isso. Beleza? Tá bom? Pode fazer com número também, tá? Também a resposta. Ã, então a gente tem aqui nono, tá? Vamos lá. 5/3 elevado 3. O 3 incide em todo mundo. Concorda comigo? Então vamos lá. 5/3
elevado 3 x 2/3, tá? Então aqui eu vou atuar, né? Eu vou botar ali o três para atuar aqui. Então é 5 elevado 3 vezes esse 2 aqui. Tô botando todo mundo já no mesmo traço, tá bom? E aqui é o 3 elevado 3 x esse 3 tá aqui, tá bom? 3 elevado 3 x 3. Vou resumir isso aqui. 5 elevado 3 x 2 dividido por 3 elevado 4. Não é isso? Que aqui eu tenho 3 elevado 3 x 3 el 1 dá 3 elevado 4. Tá? Ã, cara, vamos abrir isso aqui, né? Então, 5
el 3 é 5 25 125. 125 x 2 é 250. 250/ 3 9 27 81. Não dá para fazer mais nada aqui. 250 por 81. Beleza? Terminamos então aí todo o exercício dois. Beleza? Parabéns aí aos que assistiram a aula. Até a próxima e vamos nessa. Pronto, você finalizou agora potenciação. Já tem a teoria, já tem os exercícios. Vamos seguir agora pra radiciação, tá bom? Espero que você esteja gostando. Agora vem a teoria de radiciação, que é um assunto que ainda mais gente tem dificuldade, mas você vai ficar perfeito. Pode cair para dentro que já
tem a teoria e os exercícios. Vamos lá. Sejam todos muito bem-vindos a mais uma aula da plataforma SAD. É um prazer ter vocês aqui. Hoje a gente vai pegar a teoria completa de radiciação, tá bom? Lembrando, eu já expliquei essa teoria aqui várias vezes, em várias aulas. Eu tô sempre explicando radiciação, porém é um assunto que mesmo em para alunos avançados, isso continua gerando dúvida. Essa é a realidade, né? Que poucos são os alunos que são realmente profissionais em radiciação, tá? Então, eh, eu resolvi fazer uma aula aqui puramente teórica para resolver de vez, tá?
para resolver para sempre aí todos os problemas que existem ou que podem existir em radiciação. E vai ser isso mesmo que nós vamos fazer hoje, ok? Então, hoje a gente vai pegar pesado aqui em radiciação, vai pegar aqui todas as propriedades que existem de radiciação, tá? E a gente vai eh matar tudo de radiciação. E é o que eu falei, se você for lá no capítulo de logaritmo, você vai ter isso aqui. Se você for nos exercícios de nivelamento, você vai ter isso aqui. Em diversos lugares a gente já explicou radiciação, mas nessa aula aqui
eu vou explicar de uma maneira bem estruturada, bem didática e definitiva, tá bom? Então essa aqui é a aula suprema de radiciação. É isso que nós vamos fazer hoje e sejam todos bem-vindos. Vamos começar, tá bom? Então, bora lá. Radiciação. Quando você pensar em radiciação, você sempre vai ver essa estrutura aqui, tá bom? Essa estrutura aqui a gente chama de radical, entendido? Então, essa estrutura aqui, você vai olhar para ela, você fala: "Isso aqui é o radical", tá bom? E além de, claro, a gente chamar o símbolo de radical, a gente também acaba chamando tudo
de radical. Então, quando a gente quer se referir a tudo, a gente chama tudo de radical, tá? Então, vamos supor, eu tenho aqui, olha, a raiz de 16, não existe só√16, tá bom? Você tem que dizer quem é que tá aqui em cima. Então, vamos lá. Isso aqui é um radical, tá? Às vezes a gente chama só o símbolo de radical, mas se a gente quiser chamar tudo de radical também pode. Beleza? Então, radical ou é só o símbolo ou é o conjunto inteiro, tá? Qual é o nome do cara que tá aqui em cima?
Índice. O nome desse cara aqui é índice, tá? Você tem que gravar isso agora, tá? Não, não é, não é para você anotar, é para você gravar. Não, todo mundo já anotou isso aqui na vida, mas pouca gente gravou. Então, isso aqui é o índice. Como é que eu vou gravar que isso aqui é o índice? Ele indica. Ele indica é raiz de que tipo? É raiz quadrada, é raiz cúbica. Ele é que indica. Tá bom? É só você pensar na palavra índice. Índice não é uma palavra que já te joga para cima. Então, índice
ele tá lá em cima, ok? Índice vem de uma coisa que indica, tá? Justamente, né? O índice de um livro, ele indica onde vai estar cada coisa. E é claro que quem indica tem que estar onde? Tem que estar em cima para indicar. Eu tenho que estar em cima para eu poder indicar as coisas, né? Pode parecer bobeira isso, né? Nunca jamais em hipótese alguma vai cair na prova o que que é o índice, mas é que isso aqui vai compondo a tua inteligência, né? Então, quanto mais relações você tem de palavras, mais inteligência você
tem, tá? E quem é esse cara aqui? Ele é o radicando. Então ele é o radicando. Olha a palavra radicando. Isso não indica que tá sofrendo um processo de radiciação. Radicando. Esse ando quer dizer, olha, tá acontecendo. Ele é o radicando. Ele tá sendo radiciado. Deu para você entender? O radicando, ele é quem está sendo passando pelo processo. Beleza? Ok, então beleza, né? Exatamente. Perguntaram ali, deixa eu deixar aqui o chat para eu ler, né? Vou deixar o chat aqui para poder acompanhar o que vocês dizem. É a mesma coisa com o dividendo, né? Quando
a gente vai fazer uma divisão, né? Então vou pegar aqui, ó, vou dividir o número 20 pelo número 5 e a resposta vai dar 4. Esse aqui é o dividendo, tá sendo dividido, n? Então esse aqui é o dividendo e esse aqui é o divisor. É vai ser dividido por cinco, tá bom? Esse aqui é o cociente e aqui seria o resto, não sobrou nada. Beleza? Tá bom. Então esse aqui é o radicando e aqui é o índice. E isso aqui tudo a gente chama de radical ou às vezes a gente chama só o símbolo
de radical, tá? Como é que funciona essa estrutura de uma raiz? Tá? Eh, primeira coisa, a raiz mesmo, vamos lá, a raiz mesmo é o resultado, tá? Então, a raiz mesmo é o resultado. Resultado de quê? Primeira coisa, você tem que entender o que significa isso aqui. Quando você olhar para esses para esses símbolos aqui, você tem que saber traduzir em linguagem. Então é o seguinte, que número olhou para isso aqui? A pergunta que tá sendo feita é o seguinte, olha só. Que número que se for elevado a dois, ou seja, que número que se
for multiplicado por ele próprio duas vezes, vai dar esse cara que tá aqui dentro, tá? Então isso aqui se lê dessa forma. Olha só. Raiz quadrada de 16, OK? Sempre que a raiz tem um índice igual a 2, a gente chama de raiz quadrada, tá? Sempre que a raiz tem um índice igual a 3, a gente chama de raiz cúbica, tá? Agora, a gente também poderia chamar de raiz de índice dois, raiz de índice três, tá bom? Eh, então vamos lá. Quem é a raiz quadrada de 16? Isso é a mesma coisa que eu te
perguntar o seguinte: que número, algum número que eu não sei, né? Que número que se for multiplicado por ele mesmo duas vezes vai dar esse cara que tá aqui dentro? A resposta a gente sabe que é 4. Se o 4 for multiplicado por ele mesmo duas vezes, ele dá 16. Ou seja, quando você não sabe a raiz, você pode muito bem colocar o seguinte: "Olha, a resposta disso aqui é x. √ qu 16 é x. Mas como é que você executa isso aqui? X elevado a esse 2 tem que dar esse 16. Entendeu? X elevado
2 precisa dar 16. E que número que elevado a 2, ou seja, que multiplicado por ele mesmo 2 vezes d 16 é 4. Se você testar aqui, você vai ver que 4 elevado 2 dá 16. Entendido? OK. Perfeito. Maravilha, né? É isso, tá? Isso aqui que é raiz. Por exemplo, se eu tiver assim, olha, raiz cúbica de 27, que pergunta é essa? Qual é o número que vezes ele mesmo? Sempre começa assim. Qual é o número que vezes ele mesmo? Quantas vezes? Três vezes dá o 27. Quem é o número que vezes si próprio três
vezes dá 27? É o 3, tá? Porque o 3 vezes ele mesmo três vezes, né? Ou seja, 3 elevado 3, ou seja, 3 x 3 x 3 de novo dá 27. Beleza? Entendiu também? Tá tudo certo aí com a minha imagem, com o meu áudio, tudo padrão. OK, perfeito. Então isso aqui é raiz, tá bom? Vamos lá. Quem é a raiz qu de 64? Ou seja, que número que vezes ele mesmo quatro vezes dá o 64. Tá bom? Aliás, perdão, qual é a raiz cúbica de 64? raiz cúbica de 64. Que número vezes ele mesmo?
3 vezes dá 64. É o 4. Beleza? Você pode observar aqui 4 x 4 x 4 de novo, né? Ou seja, 4 elevado 3 dá 64. Mas muita atenção, a raiz não é 4 elevado 3. A raiz é apenas o 4. Porque isso aqui já tem uma pergunta completa, né? Já tá dizendo aqui qual é o número que elevado a ele é elevado a 3 ou qual é o número que vezes ele próprio 3 vezes dá 4. A resposta dá 64, perdão. A resposta é 4, tá bom? não é 4 elevado 3. O que você
pode fazer é olhando para essa estrutura aqui, escuta bem, você pode olhar para essa estrutura aqui e escrever-la da seguinte forma. Você pode falar assim, ó, 4 elevado 3 dá 64. Aí vai ficar 4 elevado 3 dá 64. Aí sim. Tá bom? Detalhe que tendo essa equação aqui, isso aqui é uma equação, né? 4 elevado 3 dá 64. O que que você pode fazer? Você pode pegar essa potência de três e passar pro outro lado da igualdade, desde que você passe como uma raiz de índice 3. Então aqui, ó, tá vendo aqui, ó? 4 elevado
a 3. Você deixa aqui apenas o 4 e aqui tá o 64. Esse TR passa para cá como raiz cúbica de 64. Aí a mesma coisa. Você continua mantendo aqui a identidade. OK? Todos estão aqui, todo mundo pegando. Isso aqui é o básico, tá? Básico, básico, básico, básico. Isso aqui quer dizer que a gente começou a estudar eh radiciação. OK? Perfeito. Agora vamos já direto paraas propriedades de radiciação, tá bom? Vamos lá. Primeira propriedade, vamos supor que eu tenha assim raiz, ah, esqueci de falar uma coisa, tá bom? Isso aqui é importante de ser citado.
Quando eu não tiver nenhum número aqui, é porque é uma raiz quadrada, tá bom? Então, se eu tenho assim, por exemplo, ah, √9, eu não tenho nenhum número aqui no índice, né? O índice está vazio, tá? Galera, é muito importante que vocês falem o tempo todo sobre índice, sobre, né? É importante vocês falarem isso porque isso vai fazer vocês terem intimidade com a matemática. Alguém já reparou isso que numa sala de aula ou de cursinho os escutem isso aqui que eu vou falar agora que é bem profundo, tá bom? Só para ficar na nossa mente.
Vocês sabem que eu não consigo dar aula sem falar mentorias no meio da aula, né? Então deixa isso aqui na sua mente, tá bom? Numa sala de aula, quando você observa os melhores alunos, alunos muito aplicados, estudiosos de boa família, geralmente que a família se preocupa muito com a educação, que tem uma família bem rigorosa, você vê que esses alunos eles dominam muito a linguagem matemática, eles falam as coisas mesmo, eles falam assim o índice da raiz. E você vê que os alunos ruins, né, os alunos que não se desenvolvem na matemática, são alunos que
passam anos a fio sem saber essas coisas. Eles ficam sempre tentando o quê? Um macete. Ah, corta, corta. Ah, passa para outro lado. Aqui eu mostrei o passa para outro lado, mas eu já expliquei. Vocês sabem que isso quer dizer o quê? Quando eu tenho aqui 4 elevado 3 é igual a 64 e eu decido passar isso aqui pro outro lado. Na verdade eu não tô passando pro outro lado, eu tô executando a mesma operação dos dois lados. Eu tô falando o seguinte, ó, já que isso aqui é uma igualdade, eu posso tirar a raiz
cúbica dos dois lados. Então vou tirar a raiz cúbica desse lado e vou tirar a raiz cúbica desse lado. Ocorre que uma raiz cúbica de uma potência de que tá de um de uma potência de expoente três, você corta o três com três, fica apenas o quatro. E desse lado aqui permanece o quê? A raiz cúbica de 64. Então eu não passei pro outro lado o expoente apenas, né? Eu não peguei aqui a 4 elevado 3 64 e passa pro outro lado. Isso aqui vem como uma raiz de índice 3. Na verdade eu apliquei uma
raiz 3 dos dois lados, OK? Isso é muito importante, tá? Então eh voltando aqui, tá? Quando a gente não vê o índice, é porque o índice é dois, OK? Na ausência de um índice visível, é porque o índice é dois. Você tem que saber isso desse jeito mesmo, tem que saber falar essa frase, tá? Agora, vamos lá. Vamos supor que eu tenha essa situação aqui. Eu tenho aqui, olha, a √3 ã elevado a 2. √3 elevado 2. Detalhe, tá? Eh, só um instante. Ô, alguém fecha a porta aqui, por gentileza. H, eu tenho aqui uma
raiz de 3 elevado 2, só que eu tô vendo aqui, né? Primeiro que eu não tô vendo nenhum nenhum índice. Então, é claro que o índice é dois. Isso é fato. O índice é dois mesmo. E aqui dentro do meu radicando, eu tenho um expoente, eu tenho uma potência, né? 3 elevado a 2. Ã, qual é a propriedade que eu quero passar para vocês aqui agora? Tá bom? Primeira coisa, você pode escrever aqui o índice para você visualizar mais facilmente, não tem problema nenhum. O que que você sempre pode fazer? Você pode pegar o índice
e colocar ele aqui como sendo o denominador do expoente. Basicamente vai virar isso aqui, ó. Tá vendo esse dois aqui, ó? ele entra aqui para baixo, então vai ficar 3 elevado 2. Mas agora esse dois aqui de cima é o dois que já estava aqui. E agora o dois de baixo, o denominador, é justamente o dois que veio do antigo índice. Então 3 elevado 2/ 2 é a mesma coisa que eu tinha aqui antes, quando eu tinha a raiz quadrada de 3 elevado 2. Tá bom? É claro que você vai notar que nesse caso aqui
quanto que dá 2 div por 2? Dá 1, né? Então isso aqui é a mesma coisa que 3 elevado 1, que é o próprio 3. E antes você vai ver que era isso também, né? √ qu elevado 2. Mas quem é o 3 elevado 2? É o então qual é o número que vezes ele mesmo duas vezes? Qual o número que elevado a dois vai dar? Claro que a resposta é a mesma, é três nos dois casos, tá bom? Mas agora, ã, vamos visualizar aqui mais algumas coisas, tá bom? Fica vendo mais algumas coisas ainda
sobre essa propriedade, tá? Vou mostrar agora com um exemplo em que não vai virar um no final das contas, tá? Então, por exemplo, eu tenho aqui a raiz cúbica de 9, mesma coisa, tá bom? Então, raiz cúbica de 9, vamos ver cúbica de 9. Primeira coisa muito útil que eu posso fazer é eu ter o hábito de transformar, de fator o meu radicando, tá? Então, se meu radicando aqui é nove, eu posso muito bem escrever ele como 3 elevado 2. Você vai ver que eu tô mantendo a mesma mesma coisa, não mudou nada. Então, raiz
cúbica de 9. Pô, não sei, não consigo saber que número vezes ele mesmo três vezes dá nove. Não tem nenhum número assim inteiro que vai dar isso, né? Ele vezes ele mesmo três vezes vai dar nove. Mas aí eu pego esse nove aqui e visualizo como 3 elevado 2. E o que que eu posso fazer agora? Se eu quiser visualizar de outra forma esse radical inteiro aqui? Eu pego esse três aqui e enfio ele aqui para baixo, tá bom? Então fica três aqui que é o radicando, mas ele não vai ficar elevado a dois, ele
vai ficar elevado a 2 sobre 3, entendeu? 3 elevado 2/ 3. Quem assistiu aí as últimas aulas do ciclo de nivelamento lembra disso. Porque eu tinha dito o seguinte: olha quando eu tenho aqui, por exemplo, 16 elevado a meio, ou seja, eu falei para vocês que quando eu tenho um expoente fracionário, qual é a técnica? Eu pego aqui esse denominador e eu puxo como se fosse uma toalha, né? Então eu puxo ele. Quando eu puxo ele aqui para fora, vai cair o um, né? E eu vou puxar ele aqui para fora para ele virar um
índice de raiz. Então aqui, ó, eu tenho aqui o 16. Esse dois eu faço assim, ó. puxo para fora e aí fica aqui. E esse um continua aqui embaixo, né? Esse um cai quando eu puxo uma toalha, as coisas que estão em cima caem. Então, e é óbvio que 16 elevado 1 por 16. Então, na verdade isso aqui é√ quadrada de 16, que é o número que vez ele mesmo duas vezes vai dar o 16. A resposta aqui é 4. Beleza? Então, ou seja, a única coisa que eu quero passar com essa propriedade é isso,
tá? É uma coisa aí bem simples que eu tô querendo passar, que é só você saber fazer a transição entre o índice virar o denominador da potência, beleza? Até aqui é bem básico, né? Até aqui é bem básico mesmo, tá? Então vamos pegar um exemplo aqui um pouco mais avançado. Se eu tenho aqui, olha, ra 4 elevado 3, como é que você pode reescrever isso? Esse é a mesma coisa do que o 4 elevado 3/ 5. Já começa por aí, tá? É a mesma coisa do que o 4 elevado ao 3/ 5. Todo mundo entendeu
por quê? Mesma coisa, tá? Eu peguei aqui o índice cinco e eu vi passei aqui para baixo. Tá bom, Pedro? Eu poderia ter feito de uma maneira diferente, poderia, né? Então vou, eu já vou sempre mostrando várias propriedades ao mesmo tempo, tá bom? Não, eu não mostro as propriedades em sequência uma vez só. Vou ficar voltando nas mesmas. Então, primeira coisa, o quatro poderia ter sido escrito como 2 elevado 2. Poderia. O 4 poderia ter sido escrito como 2 elevado 2. Mas lembrando que o 4 ele estava elevado a 3. Então é 2 elevado 2
e tudo isso elevado a 3. Isso aqui é só para quem viu lá a aula de potenciação, né? Porque isso aqui é propriedade de potenciação. Então agora, ó, mantendo ali a√5ª, mas aqui dentro tem 2 elevado 2, que é o 4 elevado 3. O que que eu faço com esses expoentes aqui? Eu multiplico eles, lembra? Aula de potenciação. Quem tem dúvida tem que assistir lá. Então, 2 elevado a quem? A 6. Na verdade, é 2 elevado 6. Percebeu? Visualizou? Porque eu faço aqui 2 x 3, tá bom? Eu tenho liberdade de manipular aqui o radicando.
No caso que eu escolhi pegar o 4 e transformar o 4 em 2 elevado a 2. Lembrando que o 4 inteiro tá elevado a 3. Então isso aqui dá 2 elevado a 6. Agora o que que eu faço? Eu digo que isso aqui na verdade é 2 elevado qu puxa o 5 para baixo do 6. Então é 2 elevado 6/5. É a mesma coisa do que tá aqui. Mesma coisa. Por que que eu tô mostrando isso aqui? Porque às vezes na hora da prova vai que o que tá escrito de uma forma ou de outra
nas alternativas e aí você não vai conseguir marcar alternativa porque você não tá visualizando. Inclusive no Enem 2024 agora caiu isso, tá? Eu te garanto que no Enem 2024 caiu exatamente isso aqui. Caiu uma questão em que você precisava justamente, você chegava na resposta fácil, mas você tinha que saber manipular os expoentes desse jeito aqui, desse jeito mesmo, tá? E era bem complexo de fazer se você não tivesse uma base muito forte em radiciação, tá? Então tudo que eu tô explicando aqui é exatamente isso. Essa questão aí é bem fundamentado nisso. A gente vai até
resolver ela para eu mostrar para vocês, tá bom? Pronto. Então a gente já pegou aqui as primeiras propriedades, certo? Primeira propriedade possível é essa, é transformar o que é denominador, eh, transformar o que é índice em denominador. Tudo bem? Vou agora escrever essa propriedade assim em linguagem matemática para vocês, tá? Porque eu acho que sempre vale a pena também a gente ver em linguagem matemática. Supondo que eu tenho aqui um radicando a elevado a m e tudo isso tá numa raiz de índice n, eu posso transformar isso aqui em a que tá elevado a m
sobre n. Entendeu? Deu para você sacar? É. Isso aqui é tudo, né, o que eu acabei de mostrar. É só a consolidação matemática do que eu acabei de mostrar para vocês, tá bom? Maravilha. Beleza, agora vamos pra próxima propriedade, tá bom? Tô sempre observando aqui o feedback de vocês aqui pelo pelo pelo chat, tá? Vamos lá, vamos pra próxima propriedade. Vamos supor que eu tenha, sei lá, essa aqui é boa, ó. Eu tenho aqui uma raiz em geral e ela é uma raiz de 16. Vamos reescrever essa raiz aqui para poder mostrar algumas coisas. Então,
tem raiz quadrada 16. A gente já sabe que a resposta disso aqui é 4, tá? Mas vamos supor que eu queira visualizar o 16 como sendo 2 elevado 4. Eu tô certo ainda. Eu tô falando do mesmo número. Eu tô falando de √16 ou tô falando de √2 elevado 4. Dá no mesmo 2 elevado 4 é o próprio 16. E quem é o meu índice aqui? É dois, porque não tá mostrando ninguém aqui. Não tem nenhum índice visível, então o índice é dois. Beleza? A única coisa que eu quero mostrar é uma possibilidade que você
tem. Que que você pode fazer caso você queira? Você pode pegar o índice e o expoente do radicando. Então, pega o radicando, que é o 2 elevado 4, pega o expoente dele. Você pode pegar o índice e o expoente do radicando e você pode multiplicá-los ou dividi-los pelo mesmo número sem mudar nada. Por exemplo, se eu quiser agora multiplicar por dois, tanto o índice quanto o expoente, eu posso fazer isso? Posso tranquilamente? Vou fazer agora. Quer ver? Lembra do índice? O índice agora era dois, né? Eu vou multiplicar por dois. Beleza? Então agora ele virou
4, tá? Agora, tá vendo aqui o expoente que era quatro? Primeiro que eu não vou fazer nada com dois, mas tá vendo o expoente que era quatro? Eu também vou duplicar. Eu dupliquei o índice e o expoente. Então o índice que era dois virou quatro, o expoente que era quatro virou. Dupliquei os dois, tá legítimo. É a mesma coisa de antes. Nada mudou aqui, tá? A√ qu elevado 8 vai ser a mesma coisa que a√ quada de 2 elevado 4. Quer ver quanto que é a√ quadrada de 2 elevado 4? 2 el 4 a gente
sabe que é 16. Que número vezes ele mesmo? Duas vezes vai dar o 16. 4. Agora, quanto que é a√ qu el 8? Primeira coisa, o que que é mesmo se 2 elevado 8? O 2 elevado 8 é o 256, né? Depois viraria aqui antes 12.24 é o 256. Tá bom? Então vamos lá. Eu quero a√ quarta do 256. É a mesma coisa, tá? E aí, que número vezes ele mesmo? Quatro vezes vai dar o 256? É o 4. Ou 4 elevado 4, né? 4 x 4 16 x 4= 64 x 4 256. Então, ou
seja, continua sendo a mesma resposta, não alterou nada. Entendeu? Eu posso multiplicar ou dividir, tá, o índice e o expoente do radicando, o índice e o expoente do radicando pelo mesmo número, tá? Mas, Pedro, nesse caso aqui, por que que você não escolheu dividir o índice e o expoente do radicando por dois? Eu poderia fazer, ótimo. Tá? Então, eu posso fazer isso. Beleza? Então, vamos lá. Eu vou pegar o dois e o quatro aqui e vou dividir por dois. Fecha essa porta direito aí que tá ficando barulho aí quando vocês saem, tá boa? Então, olha
só, vou dividir por dois tanto esse índice aqui quanto esse expoente. Perfeito. Divid isso aqui por dois, vai ficar um. Divide isso aqui por dois, vai ficar dois. Só que não existe raiz de índice 1. E ela some. Raiz de índice 1, ela desaparece, tá? E aí fica só o quê? O dois que em vez de tá elevado a 4, tá elevado a 2. Quanto que dá isso aqui? Quatro. É a mesma resposta de antes. Entendeu? A manutenção da identidade? Entendeu? Como que isso não altera em nada? quer visualizar agora matematicamente, vou te mostrar como
é que é isso aqui matematicamente, tá bom? Matematicamente seria desse jeito aqui, ó. Suponha que eu tenho uma raiz de um radicando que é a elevado a m e essa é uma raiz de índice n. O que que quer dizer? Quer dizer o seguinte, que eu posso chegar aqui e multiplicar esse n por x, desde que eu venho aqui e também multiplique o m pelo mesmo x. Acabou? Acabou. Entendeu? Fizeram uma pergunta ali para mim, falaram: "Qual é a raiz sexta de 64 ao cubo?" sei lá, raiz se tupla, né? Raiz de índice 6 do
64 ao cubo. Olha a pergunta que ele me faz, né? Então, não sei que que eu vou tentar fazer aqui. É, é até bom ele ter me feito essa pergunta, né? O moleque fez uma pergunta ali, porque eh isso abre possibilidade pra gente pensar, tá? Então, a primeira coisa que eu vou observar aqui é o seguinte, cara. Eu sempre posso pegar o índice e o expoente de dentro e fazer a mesma divisão. Então eu vou vou dividir pelo mesmo número. Então, por exemplo, vou dividir por três, tanto esse cara aqui quanto o de dentro. Vou
dividir por três tanto o índice quanto o expoente, né? Perfeito. Então, divide isso aqui por três, vai ficar o quê? Uma raiz quadrada. Já começa por aí. Vai ficar uma raiz quadrada. E divide o 64 elevado 3. Divide só o expoente por 3, vai ficar o quê? 1. Ou seja, vai virar o próprio 64. É oito a resposta. √ qu 64. que número vezes ele mesmo duas vezes dá 648. Entendeu? Compreendeu? Essa é a utilidade da coisa, né? Então, olha que maravilha, né? É você eh você visualizar que você ganha essas ferramentas. Mas detalhe, isso
é só uma ferramenta. Vamos puxar outra propriedade para resolver isso aqui. Agora, galera, eu tô falando, isso é o fundamental. explicar as propriedades de radiciação, eu consigo fazer em 5 minutos, mas em geral é isso, as pessoas explicam elas listando. Eu não faço listando, eu fico usando elas repetidamente, alopradamente, tá bom? Então, por exemplo, eh, que que eu posso fazer aqui com essa fração Pedro? Eu não poderia pegar o índice e enfiar aqui embaixo, enfiar aqui embaixo como se fosse o denominador do expoente? Poderia. Então, aqui, ó, 64 elevado 3, mas aí tu pegou o
índice, em fio ali embaixo, ó, ele tá elevado a 3/ 6. É a mesma coisa. Concorda? Mas quanto que é o 3/ 6? 64 el 3/ 6. É 3/ 6 é a mesma coisa que 1 sobre 2, né? A mesma coisa que meio. Então pronto, 1 2. Mas como é que é essa propriedade mesmo do denominador? Da mesma forma que tu pode enfiar o denominador para baixo do expoentes, você pode puxar de volta como o índice da raiz. Então você tem aqui agora 64 elevado 1/ 2. Você pode pegar esse dois e puxar para fora
como índice de raiz, né? Então tu fica com 64 e aí esse dois vai para fora pro índice de raiz. Aqui ficou só um, não muda nada. √64 é 8. Eh, vocês vão perceber que todas as propriedades elas são a mesma coisa no fundo. Todas são a mesma coisa. É tudo redundante, tudo. Todas as propriedades, sem exceção, não tem nada de diferente nelas. Elas são só formas de você visualizar atalhos, tá bom? E você tem que saber relacionar uma com a outra sempre, tá? Pedro, fala aí um outro jeito de lidar com isso. Falaram ali,
fala outro jeito. Então, pera aí. Eh, eu tenho aqui raiz sextupla de 64 elevado 3. Eu vou visualizar, vou transformar o 64 numa potência de base 2. Por exemplo, o 64 ele é o 2 elevado 6. 64 é isso. Concorda comigo? Então, pera aí. Eu tenho aqui √6 dupla de 64, mas quem é 64? É 2 elevado 6. Só que tudo isso ainda tá elevado a 3, né? 64 é o 2 elevado a 6, mas tá bom, mas tá tudo elevado a 3. Então fica o quê? Fica a raiz sexupla. Deixa eu fazer mais bonito
aqui que tá ficando aloprada a minha letra. Sua de 2 elevado a 12. Porque eu só multiplico as potências. Quando eu tenho potência de uma potência entre parênteses, eu faço 6 x aqui é 3, né? Fica 18, tá? Então 18. Beleza? Agora o que que eu faço? Eu posso dividir sempre o índice e o expoente do radicando pelo mesmo número. Então vou dividir os dois por seis. Bacana, né? Dividir aqui por 6 virou 1. Ou seja, a raiz morreu. Dividi aqui por 6 virou o quê? 3. 2 elevado 3. E 2 elevado 3 dá o
quê? 8. mesma resposta ainda consistentemente tá sempre dando oito. Qualquer propriedade que eu utilize aqui vai fazer isso, OK? Posso antes de executar essa multiplicação aqui já fazer na verdade o seis com esse três? Pode. Se tu considerar isso aqui é o radicando, isso aqui é o expoente do radicando. Então tu pega só o seis com três, divide por três. Então aqui sumiu o três, vai ficar aqui dentro apenas o 2 a se e aqui esse se foi dividido por 3, virou 2. Agora eu tenho √ quadrada de 2 a 6. Agora eu pego esse
2 e 6, divido por dois. Aqui virou um e aqui eu dividi por dois, virou três de novo. 2 a 8. Todas as propriedades são a mesma coisa sempre. Todas. Todas. O interessante é que você não vê muitas pessoas falarem isso. Você não vê as pessoas falarem que todas as propriedades são a mesma coisa. Na verdade, eles falam: "Ó, são várias propriedades, importantíssimo. Tem que saber tudo aqui." Aí explica tudo com as letrinhas, né? Bota só desse jeito aqui. Como é que você vai aprender desse jeito, pô? Tem que saber que tudo é a mesma
coisa. Sempre é tudo a mesma coisa. Tudo leva pro mesmo lugar. Por quê? Porque é tudo uma operação só. radiciação. As regras são, é, é uma regra só para radiciação. A única regra é o número que tá e aqui é o índice, esse aqui é o radicando e isso aqui vai dar x. X elevado ao índice tem que dar o radicando. Essa é a única regra. OK? Vamos nessa, então. Vamos continuar. Então, nem preciso falar, né? Mas vou falar, tá vendo essa daqui? Essa propriedade aqui, eu vou escrever de outra forma agora. Beleza? Então o
seguinte, se eu tenho aqui um radicando a elevado a m e tem o índice nessa raiz, eu posso também eu posso não apenas multiplicar por x aqui tanto o índice quanto o expoente. Eu eu falei que eu posso fazer isso. Falei: "Posso sim, posso, mas eu também tinha dito que eu posso dividir. Eu fiz isso agora várias vezes. Eu só vou expressar matematicamente, tá bom? Isso quer dizer o quê? Uma raiz que tem qual índice? N sobre x, ela vai ser a mesma coisa que uma raiz que tem um radicando expoente m sobre x. Ou
seja, eu dividi por x nos dois casos e eu multipliquei por x nos dois casos e eu preservo a identidade da equação. OK? Beleza? Entendeu? Pronto, né? Tá. Um exemplinho a mais aqui, Pedro, bati de frente aqui com, sei lá, raiz qua de 256. Ã, sei lá, visualizei o 256 como 2 elevado 8. Então, eu tenho a√ qu elevado 8. Quero dividir o qu e o 8 por 4. Ótimo. Dividiu por quatro, morreu. Virou, virou um. Não é mais nem nenhum radical. Isso aqui já matou o radical. Assim como uma fração sobre um, tu mata
a fração também. E aqui tu divide por 4, fica 2 elevado 2, que dá 4. De fato, √4 256 é 4.6. Ok? Beleza. Matamos aqui de novo. Tá bom. Só mais um exemplo aí de aplicação da mesma propriedade, tá bom? Vamos outra propriedade, deixa eu pensar aqui. Outra propriedade é o seguinte. Multiplicação de radicais de mesmo índice. Multiplicação de radicais de mesmo índice. Então, multiplicação de radicais de mesmo índice. Sei lá, vamos lá. Eu tenho aqui uma raiz de 9, quero multiplicar ela por uma raiz 4. O índice é o mesmo, né? Concorda? O índice
é o mesmo. É, o índice é dois. Não dá para ver, mas é claro que o índice é dois nos dois casos, tá bom? Então, o que que acontece? Quando eu tenho essa situação para eu fazer a multiplicação desses radicais aqui, eu simplesmente posso englobá-los no mesmo, posso visualizá-los com o mesmo índice, né, dentro do mesmo radical e fazer diretamente a multiplicação dos radicandos. Então eu faço 9 x 4, que dá o quê? 36. OK? Você vai ver que isso é muito simples, na verdade, né? Então vamos lá. √9. Vamos botar as respostas embaixo. Quanto
que era a √9? 3 vezes a √4. Isso aqui aqui eu já resolvi, né? Eu já tirei do radical. A√4 quanto que é? 2. Quanto que daria? 3 x 2? 6. E aqui do jeito de cima, né? Eu fiz √9 x √4, mas eles tm o mesmo índice. Então eu vou multiplicar e aglomerar. Eu vou fazer o produto aqui desses radicandos no mesmo índice. Então na verdade √ qu. Mas quanto que é√ quada 36? É 6. Ou seja, consistente. Mais uma vez nada mudou. OK? Isso é muito útil aí. Tá bom. muito útil de vários
sentidos. Então, por exemplo, vamos fazer o inverso. Quando eu tenho aqui √14, aí você fala: "Porra, eu não sei a raiz de 144". Você pode tranquilamente decompor essa raiz e observá-la assim, ó. √14 é a√4 x 36. Normal, pô, Pedro, e se eu quisesse escrever que é a√4 a √36? Também pode, entendeu? Também pode. Você pode ou visualizar o mesmo chapeuzinho, né? o mesmo radical com os dois com o produto dentro ou pode separar, mas dá no mesmo, tá bom? O que importa é que é tudo aqui do mesmo índice, então você tem essa liberdade
de fazer isso, tá? Inclusive aqui, né, quando a gente tem assim √9 x √4, se você quiser visualizar aqui primeiro a gente faz √9 x √4 dentro do √9 x 4 dentro do chapeuzinho para só depois fazer √36 também pode, tá bom? É só para você entender que eh dá exatamente no mesmo, tá bom? entre eu ter assim, olha, √9 x 4 e eu ter, ela é executada 9 x 4√36, é a mesma coisa também, ok? Beleza? E aí aqui nesse caso, né, eu tendo √4 x 36, eu poderia observar que a √4 a resposta
é 2 e a √36 a resposta é 6. E aí com isso eu tenho que a resposta dá 12. √14 de fato, é 12. 12 vezes ele mesmo, duas vezes 12² dá 144. Beleza? Todo mundo tranquilo com isso? OK. Certo? Vamos lá então. Ã, e agora, né, tem outra aplicabilidade dessa propriedade? Tem a aplicabilidade da divisão, né? Se você tiver assim, olha, eu tenho a raiz de 36 dividida pela raiz 9. Ah, como é que eu faço divisão de de de radicais? Cara, eles têm o mesmo índice. Se eles têm o mesmo índice, você pode
tranquilamente dizer que isso aqui tudo, na verdade, é raiz de quê? √3/ 9 no mesmo índice. E aí, √3, quanto que é 36/ 9? Apenas isso. 36/ 9 é 4. Então, na verdade, isso aqui é a√4. E a√4 a gente sabe que a resposta é 2, entendeu? É claro, se você tivesse antes feito √36 6 √9 3, 6 por 3 também dá 2. Claro, eu tô só mostrando a propriedade, né? Em um exemplo sempre fácil de entender. Não tem porque eu mostrar a propriedade de modo abstrato. Vou mostrar a propriedade do jeito que você consiga
visualizar ela rápido, tá bom? Ou seja, que propriedade é essa, né? Vamos colocar a propriedade aqui agora na linguagem matemática, tá bom? Então vamos lá. A propriedade é a seguinte. Eu tenho aqui a raiz de a no índice n vezes a raiz b no índice n. E isso é a mesma coisa que a raiz enésima, né? Raiz de índice n de quem? AB. OK? Beleza? Só isso. Beleza? Tranquilo. Muito simples, né? Eu tenho aqui a raiz enésima de a dividido pela raiz enésima, né? Raiz de índice n de b. E isso é a mesma coisa
que a raiz enésima da divisão do A pelo B. Fazendo multiplicação ou divisão de mesmo índice, é moleza. Eu só me preocupo mesmo com os radicantes. Eu multiplico eles ou divido eles. Ok? Entendido? Acho que eu já dei bastante exemplos aí, né? Ã, pronto. Mas é, alguns casos assim são mais usuais, né? Então, por exemplo, esse caso aqui é um caso muito bom para dar exemplo. Eu tenho √27, imagina que aparece na prova para você, √27 dividido por √3. Olha como é que esse caso aqui é muito bom, né? Você sabe quanto é a √27?
Que número vezes ele mesmo duas vezes dá 27? Não, pô. Não tem nenhum número inteiro que vezes ele mesmo duas vezes dá 27, né? 3 x 3 dá 9. 4 x 4 dá 16. 5 x 5 dá 25. 6 x 6 dá 36. E que número vezes ele mesmo dá 3? Pô, também não não tá não tem esse número inteiro, né? √3 é 1,71, tá? Ok? Então o que que você faz? Justamente isso, né? O bom é que tá no mesmo índice, né? Índice o quê? Dois, né? As raízes aqui são índice índice dois. Que
que você pode fazer? Você pode falar assim: "Ah, na verdade isso aqui é a√27 di por 3. Na verdade isso aqui é a√9, porque 27 por 3 dá 9. √9 é o quê? 3. Ó que maravilha. Você sai de uma conta impossível de você solucionar no na hora da prova. Impossível. Não tem como você saber isso aqui. Nenhum desses aqui tem raiz exata para uma conta ridícula dessa. Entendido? Tudo certinho? Beleza. Então, matamos aí mais uma propriedade e também ficou demonstrada a sua aplicabilidade. OK? Acho que tá ficando tranquilo aqui, né, o resumo das propriedades.
Vamos mais uma agora. Vamos lá. Deixa eu ver aqui uma propriedade bacana pra gente pegar agora. Ã, eu diria propriedade, tô tentando lembrar da ordem, coloquei propriedade do expoente, quando tem um expoente num radicando inteiro, tá? Então, vamos lá. Quando a gente tem um expoente em um radicando inteiro, esse expoente, na verdade, ele entra eh quando a gente tem um expoente, perdão, no radical inteiro. Quando a gente tem um expoente no radical inteiro, esse expoente, na verdade, vai entrar dentro do radicando. Como assim? Sei lá, vamos supor que eu tenho assim, olha, raiz de 3,
eu tenho √3, beleza? Não tem, né? A gente não sabe a√3 de cabeça. √ qu número vezes ele mesmo duas vezes dá 3. Não sei, ó. a gente, eu sei que a resposta é 1,72, mas é só porque eu tenho isso de cabeça. Mas vamos supor que eu tenha a √3². Primeira coisa, tá toda ela ao quadrado, tá? O radical ao quadrado, né? O que significa uma coisa está ao quadrado? Quer dizer que ela vai ser multiplicada por ela mesma duas vezes, né? Então, antes de eu mostrar a propriedade, vamos tentar executar braçalmente. Vamos lá.
√3². Isso aqui não é a mesma coisa que eu dizia, olha, isso aqui vai ser multiplicado por ele mesmo duas vezes. Então, sim, √3 x √3. Mas isso aqui não é por acaso ã uma multiplicação de radicais de mesmo índice? Então eu não posso simplesmente não é zero não, tá bom? Só tô tipo circulando uma bolinha aqui, beleza? Não posso, é o índice aqui é dois, claro. Eu não posso simplesmente multiplicar aqui os radicândos e colocar a resposta. Então aqui, ó, 3 x 3 dá 9. Então é a mesma coisa, né? √3 x √3 é
√9. E √9, na verdade, a gente sabe que a resposta é 3. A resposta é três, entendeu? Perguntaram se o índice fosse zero, não tem índice zero, tá bom? Índice nunca é zero e nem um. Índice ele é um número natural maior que um, tá? Então o índice é dois para cima, ok? Então isso aqui que eu mostrei agora é o resultado é três. Mas qual é a propriedade que facilita que a gente encontre isso aqui? Tá bom? E e não, isso aqui não vale se o se o radicando for não vale não tem nenhuma
dessas regras não. Se o radicando for igual, nada disso. É só que eu tô mostrando aqui de um nível bem fácil, mas eu vou mostrar para vocês. Olha só. Vamos lá. Eh, o que que tem que acontecer aqui? Tá vendo esse expoente? Ele tem que entrar aqui, tem que multiplicar aqui o expoente atual, tá? Do radicando. Então, o expoente aqui não é um. Esse é o expoente do radicando. Você concorda? Você vai chegar aqui com dois e vai trazer o dois para cá, tá bom? Então, na verdade, isso aqui é a mesma coisa que a√3
elevado 2. OK? Perfeito. √3 elevado 2. E aí você lembra daquela propriedade, né? Claro que √3 elevado 2 é a mesma coisa que √9 que dá 3. Mas se você lembrar também, eu tenho aqui o índice dois e o expoente do radicando sendo 2. Eu posso dividir eles pelo mesmo número, né? Posso dividir por dois aqui e por dois aqui e vai dar o mesmo três. Você entendeu? Visualizou? Ok. Então a potência que tá aqui, né? A potência que tá englobando todo o radical, ela se transforma na potência do radicando em si, tá bom? É
assim que funciona, tá? Ah, perguntaram: "Mas por que que o índice também não sofre alteração, né? Por que que o índice também não não é multiplicado?" É, como é que você faz multiplicação de raízes? Você não multiplica o índice junto. O índice aqui é dois, né? E você não vai multiplicar ele junto. Você vai repetir ele mesmo, tá? Você vai simplesmente fazer eh √3 x √3 é √9. Vai preservar aqui o índice, tá? Então não vai alterar em nada. Beleza? Entendeu? Pegou? Show. Então mais uma propriedade aí foi ã compreendida, tá? Vou escrever essa propriedade
aqui também matematicamente, né? Vocês estão gostando que eu tô escrevendo assim? Tá ajudando aí na aula? Isso ajuda? Eu escrev o jeito que eu tô fazendo aqui tá sendo bom para vocês. Preciso de feedback, né? Que vocês para vocês que são os alunos, tá? Então vou colocar agora essa propriedade, tá bom? Vamos supor que eu tenha uma raiz do número a e essa é uma raiz de índice n e toda ela tá elevada a um expoente m. O que vai acontecer é isso aqui, tá? A gente vai ter aqui agora isso é a mesma coisa
do que a raiz do a elevado ao m. O m vai entrar direto ali pro radicando, tá bom? Entendido? Ã, então é isso, né? Se eu tivesse, se eu te perguntasse assim, qual é, deixa eu ver aqui um exemplo, qual é a raiz, sei lá, a raiz nona pegar uma coisa difícil, a raiz non de 27, só que tudo isso aqui eu quero que seja elevado a três, né? Eu ia já ia pegar e enfiar o três aqui dentro direto, tá bom? Então, na verdade, isso aqui ia ser a raiz nona de 27 el 3.
Tá bom? E agora, o que que eu ia fazer? Agora eu ia dividir tanto o índice nove quanto o expoente, ia dividir os dois por três, tá bom? Então ia dividir aqui por três e por três, na verdade eu ia est pedindo a raiz cúbica de quem? A raiz cúbica de 27. E a raiz cúbica de 27 é o 3. Beleza? Então, ó, que maravilha, né? Se eu também poderia ter visualizado aqui o o É, não, aqui não. É isso mesmo. É, eu poderia ter visualizado o 27 aqui como 3 elevado 3, né? E dividir
de novo aqui por três e aqui por três e chegar no três do mesmo jeito. Beleza? OK. Então, mais uma propriedade aí foi, acredito que bem assimilada, tá bom? OK. Maravilha, né? Deixa eu ver aqui agora. Há uma propriedade que deriva dessa, né? A propriedade que é o inverso dessa aqui, basicamente é o seguinte: e quando eu tenho uma raiz de uma raiz, essa é outra propriedade importante para você dominar, tá? Quando eu tenho uma raiz de uma raiz, então, por exemplo, pensar aqui num exemplo clássico, quando eu tenho aqui a raiz da raiz cúbica
de 64, muita gente pode se confundir com isso aí, tá bom? Mas é bem fácil. É só você visualizar aqui que o índice é dois e você multiplica os índices. Acabou. Só multiplicar os índices, tá bom? Então, a raiz quadrada da raiz cúbica de 64 nada mais é do que a raiz sexta de 64. Nada mais é do que isso, tá bom? Ã, e a raiz sexta de 64 é 2, tá bom? Que número vezes ele mesmo? 6 vezes dá 64. 2 2 x 2 x 2 x 2 x 2 x 2. Tá bom? Se
quiser visualizar que é a raiz sexta de 64, quem é o 64? 64 é o 2 elevado 6, tá bom? Então a gente coloca aqui 2 elevado 6 e simplifica aqui o índice com o expoente. Cortou, cortou, a resposta vai ser a mesma, vai ser dois. Tá bom? E aí, deu para entender? Deu para sacar? Claro, galera. Estão me perguntando se dá para resolver primeiro a que tá aqui dentro, depois aqui fora. Claro, claro, né? Óbvio, tá? Com certeza. Tá? Então aqui, ó, quem é a raiz cúbica de 64? Que número vezes ele mesmo? 3
vezes dá o 64? É o quatro, né? Então vou trocar só isso aqui pelo quatro. Então ficou ali raiz quadrada de quem? da raiz cúbica de 64, que é o 4. Quem é a√ quadrada de 4? 2, entendeu? Mas você pode ter certeza que existem momentos em que vai ser muito conveniente você usar essa propriedade, entendeu? Vai ser muito conveniente você só multiplicar aqui para você poder seguir em frente no problema, tá? Então a gente vai perceber isso mais paraa frente, especialmente quando for estudar função exponencial e logaritmo, você vai ver eh onde que isso
aqui vai chegar, tá bom? Então é isso, né? Acho que até então tá tudo fixo. Deixa eu colocar aqui agora essa outra propriedade, tá? Então, quando eu tenho a raiz de um número a que tá elevado a um expoente n e essa raiz tem um índice m, hã, pera aí. Quando eu tenho a raiz de um número a, eu tenho aqui uma raiz de índice n e eu tenho uma raiz disso de índice m, isso é a mesma coisa que a raiz de índice n x m do mesmo expoente a. É isso, tá? A maioria
esmagadora dos alunos vai ter impossibilidade total de progredir em log e exponencial por não saber isso aqui. Pode ter certeza. Tá bom? Claro que do meu jeito, né? Quando você vai lá ver o capítulo de logaritmo, mesmo que você não saiba nada, você ainda consegue aprender. Mas não tem comparação. Para quem já sabe, isso aqui vai aprender muito mais rápido, tá bom? Perfeito. Ã, então é isso, tá? Acredito que aqui a gente já pegou o grosso, mas tem mais coisa com certeza. Deixa eu puxar aqui da minha cabeça. Deixa eu tentar lembrar aqui. Eu vou
mostrar agora. Ah, tá. Acabei de lembrar que tem tem umas coisas aqui. Ã, tem umas coisas aqui importantes. Tá bom, vamos lá. Deixa eu pegar aqui um exemplo. Eu vou mostrar agora algumas operações entre raízes, tá? Operações entre radicais, tá? E depois eu vou mostrar mais coisa ainda. Então, eu lembrei agora aqui de operações entre radicais. Essa aqui é muito boa, tá bom? Vamos lá. Vamos supor que você queira fazer uma soma. Tem muita gente pergunta isso, né? soma de frações. Primeira coisa, eu vou ter que explicar aqui o conceito de radicais semelhantes, tá? Eh,
isso aqui é um conceito mesmo, radicais semelhantes. O que são radicais semelhantes? Radicais semelhantes são radicais que t o mesmo índice, tá? E o mesmo radicando. Isso é, isso são radicais semelhantes, tá bom? tem que ter o mesmo índice e o mesmo radicando. Então, por exemplo, ã, vamos supor que eu tenho assim, olha só, eu tenho aqui √9. Esse radical aqui, ele é semelhante a quem? Ele é semelhante ao radical √9. Você fala assim: "Ué, eh, então raiz quadrada 9 é semelhante a√ quadrada 9." Exatamente isso, né? Tem o mesmo índice, o índice é dois
e tem o mesmo radicando. O radicando é nove. Aí tu fala: "Mas qual a utilidade disso?" A utilidade disso eu te falar que se você quiser somar esses radicais, você vai visualizar o quê? Eu tenho um desse aqui e tenho um desse. Eu tenho 1√ qu 9 + 1√ qu9. Então eu tenho o quê? 2 duas, né? Raizes quadradas de 9. Entendeu? Pode parecer bobeira, mas muita gente vai ficar pegado nisso aqui, tá bom? Então é isso, tá? Deixa eu deixa eu escrever mais agora aqui. Vamos supor que tu tem assim, olha só. [Música] 5√
7 + 13√7. O quanto que dá isso aqui? Isso aqui dá 18 √7, OK? Muito importante, tá? Muito, muito, muito importante. Beleza? Então, eh, esse número aqui, tem muita gente que não tá acostumado com isso, né? Porque a gente tá trabalhando muito só com e o radical ali em si, né? só só com a estrutura própria do do índice do radicando. Mas isso aqui é um número que tá multiplicando, tá? Esse número aqui que aparece do lado, ele está multiplicando é esse radical. Deu para entender? Se você quiser chamar√7 de bananas, você vai falar: "Ó,
tenho cinco bananas mais 13 bananas, eu tenho 18 bananas". Só que ele troca banana por√7, você vai visualizar. Agora, é óbvio, não é para ficar fazendo isso assim na hora da do teu do teu treinamento, né? É para você visualizar isso aqui de modo mais fluido, tá bom? Então, deixa eu te deixa eu te mostrar aqui agora algumas coisas sobre isso, tá bom? Primeira coisa é isso aqui. Vamos supor que eu tenho aqui uma um número que ele é [Música] hum é √50. Que número vezes ele próprio duas vezes dá 50? nenhum. Eu sei que
7 x 7 dá 49, sei que 8 x 8 dá 64, mas 50 não dá. Então o que que você pode fazer com ele? Você pode primeiro visualizar ele em forma de um produto, né, um pouco mais decomposto. Então, por exemplo, ele é a mesma coisa que 2 x 25, de fato. Então, √50 é a mesma coisa que √ qu 25. Que que eu posso fazer agora? Eu posso resolver uma das partes. Então, por exemplo, eu sei qual é a resposta da √25. A √25 é 5, né? Que número vezes ele mesmo dá e que
número vezes ele mesmo dá dá cinco. Dá 25. É o 5, tá? Então o que que eu faço? O 25 eu sei a resposta. é 5, eu tiro a resposta daqui, tá? Então, por exemplo, o 25 sai da raiz como quem? 5 e fica o que aqui? √2 5√2. Ou seja, qual é a √50? Ah, eu não sei exatamente quem é, mas eu sei que é 5 x√2. Pegou? É isso. 5 x √2 é a mesma coisa que a√50. 5√2, tá? E aí o que que acontece, né? Fica vendo agora onde que você você vai
chegar, tá bom? Ah, você perguntaram assim pr mim: "Mas e se a pessoa tivesse colocado aqui que isso aqui é 5 x 10?" Cara, seria teu papel perceber que isso aqui não leva lugar nenhum. 5 x 10, tá? √5 x 10, você não sabe nem a √5, nem a√10. Então, por que tu não escreve? Talvez aqui, olha só, 5 vezes, ao invés de você botar 10, por que que você não bota x? Aí agora você não tem aqui o 5 x 5. Por que que você não chama de 5²? Você pode chamar de 25 também,
né? Mas olha só, aqui eu tenho 2 que tá aqui e o 5 x 5 eu vou chamar de 5². Tu sabe quem é a √2? Não. Vamos deixar aqui √2. Tu sabe quem é a √5 elevado 2? Corta aqui o índice 2 só com esse expoente do aqui. Ele sai como cinco. É óbvio que se quiser falar que o 5 elevado 2 para depois tirar a√25 e voltar pro 5, tudo bem, né? Mas a gente sabe que a raiz quadrada, né, de qualquer número a √15 elevado 2, tu vai cortar o índice com isso
aqui, vai dar 15, né? Então, √5 elevado 2 também é o próprio 5. OK? Beleza? Deu para entender? Não tem muito erro ali, né? Agora visualiza aqui comigo o que que eu vou te mostrar, tá? Tô montando aqui o exemplo na minha cabeça, tá? Vamos lá. Montei. Vamos supor que você tivesse essa situação aqui. Imagine você essa situação aqui. Cai na prova assim, ó. Você tem, chegou no formato final ali da questão, chegou no último momento da questão e você tem isso aqui, olha só, √50 + √72. Me diz uma coisa, isso aqui são radicais
semelhantes? Claro que não. Ele tem ali o mesmo índice, né? A menina falou que por isso que vale muito a pena suas aulas, né? Tem muito professor que foca só nas regras e quando sai você não tem recurso para resolver nada. É isso mesmo. A minha aula é toda focada em te dar recurso. Então, por isso que eu tô, vocês estão vendo que eu tô pensando aqui nas coisas, eu tô puxando da minha cabeça, entendeu? Porque a aula de radiciação em qualquer lugar, ela é a mesma coisa. Qualquer livro vai ter essas propriedades, mas eu
tô tentando puxar as situações do Enem que cai. Isso do jeito que cai, tá bom? Então vamos lá. Tu, isso aqui acontece muito no Enem. Tu chega ali em √50 + √72. Como é que você vai lidar com isso aqui? Você não sabe quanto é a raiz de 50, nem quanto é a√72. Mas se você conseguisse transformar isso aqui em radicais semelhantes, seria muito bom. Mas como que eu transformo isso aqui em radicais semelhantes? Observa agora que eu vou te mostrar, beleza? Vamos lá. Primeira coisa, radicais semelhantes tem que ter ali o mesmo radicando dentro
da raiz e também tem que ter o mesmo índice. O mesmo índice é até um pouco mais simples, né? Porque o mesmo índice a gente já sabe que o índice aqui é dois para cada um. Mas vamos lá. Eu vou tentar reescrever isso aqui. Então √50 eu vou escrever como √2 x 25, sendo que a resposta do da√25 eu sei, é o 5. Então vou puxar para fora, tá bom? Então, raiz de de 25 aqui. Pronto, puxei que o resultado é 5, tá entendido? Então, 5√2, eu já transformei o √50 nisso, ele é 5 x
√2. E o √72 eu vou visualizar como sendo √2 x 36. E eu sei também a √36, né? A √36 é 6. Então, já puxo para fora o resultado. Então, agora aqui, na verdade, é 6√2. Eu posso somar isso aqui? Posso. Eu tenho 5√2 + 6√2. Na verdade, eu tenho o quê? 11√2. Tu vê que os radicais são semelhantes, né? Raiz de A raiz é tanto radicando dois quanto o índice dois. Então eu posso somar eles livremente, tá bom? Tenho cinco dessa aqui, tenho seis dessa, eu tenho 11 dessas. Deu para vocês visualizarem isso? O
mesmo vale paraa subtração, tá bom? O mesmo, mesmo mesmo vale para subtração. Então, se aqui eu tivesse ainda, pô, menos ã raiz de 196, não. √16 vai ter uma raiz exata. Se eu tivesse aqui menos raiz de 98, é a mesma coisa, tá? Mesma coisa. Eu tô fazendo aqui somas e subtrações de radicais. Eu só consigo fazer se eu tiver radicais semelhantes. Radical semelhante tem que ter índice erradicando igual, tá? Então vamos lá. A√50 a gente já sabe que a gente pode simplificar ela como sendo ã 5√2. A √72 a gente já sabe que a
gente pode simplificar ela como sendo 6√2. E a √98 eu poderia escrevê-la como sendo √2 x 49. E eu poderia e eu sei que a resposta da ra 7, né? Então já vou tirar e vou escrever que é 7√2. Eu consigo a resposta do 49, né, que é 7√2. Eu tenho 5√2 + 6√2, eu tenho 11√2 - 7√2, eu fiquei com 4√2. Essa é a resposta, entendeu? Então isso aqui é soma e subtração com radicais, tá bom? Eu preciso ter radicais semelhantes para conseguir fazer isso. Entendido? Vou pegar aqui um exemplo interessante pra gente fazer,
tá? Vamos supor que você tivesse essa situação aqui. Olha só quanto é 8√6. Então agora eu já vou te dar e no formato eh um pouco mais resolvido, mas você vai ver que também é um pouco difícil. Então 8√6 + 9√24. Como é que você lida com isso? Como é que você vai fazer isso aqui? Vocês estão percebendo já como que a base de faturação, ela é uma base realmente muito importante, né, cara? Olha só, você precisa que os radicais sejam semelhantes. Precisa, tá? O fato de ter índice dois já tá igual. Bacana. Agora eu
preciso que aqui dentro apareça o mesmo cara. E, pô, sei lá, eu tô olhando pro 24, eu tenho que ter a intuição. Eu preciso ter intuição de que esse 24 e tem um 6 ali dentro dele. Esse 24 aqui, na verdade, ele é um 4 x 6. E aí o 4 eu vou ter a resposta, vai ficar só o √6. Então vai ficar perfeito, né? Então esse aqui, por exemplo, eu não vou mexer em nada. Esse primeiro aqui vai ter o quê? Tenho 8√6 + Eu tenho aqui 9 vezes quem? Vezes a √4 x 6.
A √4 eu sei a resposta. Quem é a resposta? É 2. A resposta da √4 é 2. Então eu tenho que tirar essa resposta. Mas lembre que aqui fora eu já tenho um número nove multiplicando aqui toda essa raiz. Então essa ra que vai sair como resposta do ela vai multiplicar esse aqui. Tá entendendo? Ó, só para recapitular, o √6 já tá pronto. Não vou mexer nele. Agora quando eu pegar o o 4 e eu resolver e tirar o dois daqui, o 2 vai multiplicar esse 9. Então vai gerar um 18√6. Ficou 6 aqui dentro.
Deu para visualizar? Somando 8√6 com 18√6, eu tenho o quê? 26√6. Essa é a resposta. Essa é a resposta. Pegou? Visualizou. OK. 26√6. Mais um exemplo muito interessante. Olha isso aqui, ó. Eu tenho 5√ cbica de 81. Que número vezes ele mesmo três vezes vai dar 81? Nenhum. Não tem nenhum número inteiro que vez ele. É claro que existe algum, mas é quebradaço. Não confunda, tá? Tem um número que vai vezes ele mesmo 3 vezes vai dar 81. 3 x 3 x 3. 3 elevado 3 não dá 81, dá 27. E 9 elevado 3 também
não dá 81, dá 729, tá? Número que vezes ele mesmo três vezes vai dar 81 deve ser 4 vul alguma coisa bem complexo, né? Tá? Eu tenho isso e eu tenho cinco vezes esse número 5 vezes a raiz cúbica de 81. Beleza? E eu tenho isso menos 4√ cb 3. Pô, que número vezes ele mesmo? Três vezes dá três. Tá maluco. Deve ser 1,1, 1,2. Deve ser uma coisa muito doida, né? Então eu tenho que olhar para isso aqui e falar assim: "Cara, eu preciso transformar isso aqui em radicais semelhantes, né, para poder li dar.
Eu tenho cinco disso aqui e quatro disso aqui. Ã, eu já tô vendo que o índice tá semelhante. Legal, o índice está três. Agora eu preciso fazer com que esse 81 e esse três aqui eles sejam iguais. Eu consigo muito mais visualizar uma forma, né, do 81 dar origem a um radio canto 3, né? Então, por exemplo, aqui eu vou começar agora a mexer, tá bom? Tá todo mundo certinho vendo, tá? Então, olha só, 5 vezes a raiz cúbica de quem, cara? 81. pode ser reescrito como ã de várias formas, né? 9 x 9 e
tal, mas eu vou colocar aqui 27 x 3, isso é 81. Por que que eu botei isso, né? Porque eu sei que eu conheço a raiz cúbica do 27. A raiz cúbica do 27 é 3, inclusive, né? - 4√ cica de 3. Qual foi a vantagem que eu tive aqui nessa primeira fração? Nessa primeira, perdão, nesse primeiro radical. Olha só, √ cúbica 27 eu conheço, √ cúbica de 3 eu não conheço, eu vou deixar aqui, tá bom? Mas qual é a resposta? Eu consigo tirar a resposta do 27 daqui? A resposta do 27 aqui, o
número que vezes ele mesmo 3 x dá o 27, a√ cúbica de 27 é 3. Então, tá vendo aqui, ó? Eu resolvi essa parte, ó, e sai o número três para cá. Só que detalhe, tá vendo esse 27 que vai ser resolvido e vai virar um número três que vai sair? Ele vai multiplicar esse cinco. Então, esse 5 já vai virar um 15, né? 3 x 5 fica o quê? Aí 15 aqui, ó. O 27 saiu como 3, multiplicou aqui, ficou 15. 15√3. Visualizou 15√3. Visualizou? Eu tenho 15√ c. É a mesma coisa do que
eu ter 5√ c 81 eu ter 15√ c 3. Tá? Tá simplificado. - 4√3. Olha que maravilha. Radicais semelhantes. Radicais semelhantes. Mesmo índice e mesmo detalhe, tá bom? O índice tem que ser o mesmo um do outro e o radicando o mesmo do outro, tá bom? É só coincidência aqui que todo mundo seja igual. Esse tem que ser igual a esse. É só isso que importa, tá? Então, tenho 15 desse troço menos 4 desse troço. Eu vou ficar o quê? Com 11 desse troço. 11 de que troço? De√ cúbica de 3. Tá bom? Não viaja
não. Achando que dá para cortar, tá bom? O que você corta é com expoente aqui. Expente um. Não tem o que fazer não, tá? Corta o três com três. Não existe isso não, tá? Sen não ia ser uma fração, não ia ser 3 sobre 3 isso aqui. Beleza? Ok. E se eu fiz, se eu tivesse colocado que 81 é 9 x 9, ah, tu ia botar 9 x 9, tu não ia saber a raiz cúbica de 9. Tu ia ter que pegar um 9 e abrir em 3 x 3 e outro 9 3 x 3.
Tu ia ficar com 3 x 3 x 3 x 3. Aí tu ia juntar esses 3 ia ficar 3 elevado 3 x 3. O 3 elevado 3 tu ia tirar a raiz cúbica. Ele ia sumir, ia pr ia para fora, né? Como 3 e ia ficar só o 3 elevado a 1. Ok? Sim. Tem que tem que tem que colocar no mesmo índice aqui. Tá bom? Deu para entender? OK. Então tá bom, Pedro. Por isso, se eu tiver aqui radicais que, sei lá, eles não são semelhantes, eu não consigo colocá-los na forma semelhante. Então, por
exemplo, se eu tiver aqui, deixa eu ver se tá tudo certinho no enquadramento, tá? Se eu tiver aqui, olha, √81 + a√2, assim, eu não não tô vendo aqui agora como que eu posso lidar com isso de cara. Eu eu até sei a√25 é 5. Já vou botar aqui a resposta, mas e a raiz de de 81? É, tu também sabe, é, tá? Então tem que ter muito cuidado com isso, tá bom? Porque às vezes a gente fica meio meio bitolado tentando aplicar a propriedade, né? Pedro, não consigo. Tem que lembrar que você sabe as
respostas nesse caso. Então o a melhor forma de você fazer soma de de radicais é você, se você puder resolver eles, você resolve, tá bom? Esses métodos aqui é para quando você não resolve você vai chegar numa resposta melhor, tá? Porque se eu tiver assim, olha, √5 + √3 - √2, tem como fazer? Não tem como fazer nada aqui, nada. Você vai ter que saber o valor de cada um deles, tá bom? Então vai ter que ter os valores aí, mas isso não cai na prova. Essa é a coisa boa. Isso não cai na prova,
tá bom? Mas você teria que saber que a √5 é mais ou menos 2,25, que a√3 é mais ou menos 1,72, que a√2 é mais ou menos 1,41. Mas isso não vai de fato cair na prova. Tá bom? Vamos mais coisa. Eu expliquei tudo, tudo, tudo, tudo sobre ã tudo sobre soma e subtração de radicais. Falei que eles têm que estar na forma semelhante, tá? e mostrei como que você conduz a coisa para forma semelhante quando é possível, tá? Agora vamos pensar aqui de novo, né? Vamos revisar multiplicação e divisão, tá bom? Então vamos supor
que você queira fazer aí a multiplicação de de radicais ã que eles estão com o mesmo índice. Eu já expliquei isso, vocês lembram? Então tô com aqui um radical que tem índice três. Então tenho aqui a raiz cúbica de raiz cúbica 27 e tô multiplicando isso aqui pela raiz cúbica de 9. Isso aqui é a mesma coisa. do que a raiz cúbica de 9 x 27, tá bom? Raiz cúbica de 9 x 27, ou seja, raiz cúbica de ã 243. Beleza? É isso, tá? Que eu nem sei qual é a resposta, nem tenho uma resposta
exata para isso, tá? Mas só para ilustrar para vocês aqui, isso aqui é a mesma coisa, né? Então só tô recapitulando para ficar bem organizado. Eu já expliquei essa propriedade, mas a gente apenas repete o índice e executa ali o produto, ok? Se for uma divisão, mesma coisa, tá bom? Então, se eu tenho ali uma raiz, vou mostrar de novo, né? Tenho ali raiz quarta, sei lá, raiz quarta de ã, sei lá, qualquer coisa, √ qu, não sei, dividido aqui pela raiz qu de 5. Isso é a mesma coisa que a√ qu de quê? De
100 di por 5, tá bom? Qu, no caso, que também não tem uma resposta exata, né? Mas estamos colocando aqui só para mostrar de novo propriedade, tá bom? Perguntaram se a resposta disso aqui é 9, não, né? 9 x 9 dá 81. 9 de novo dá 700 e 72, tá? Ah, não, 729, tá? Então, sacou? Quando a gente tem esses índices iguais aqui, eu já tinha mostrado, né? Eu só tô mostrando novamente, tá bom? Agora vem o caso interessante, né? Por isso que eu tava mostrando isso para poder pegar o caso mais interessante. E quando
eu tenho radicais com índices diferentes, tá? Então, exemplo clássico aqui, vamos supor que eu tenha √6 x √3, tá bom? Só que o índice não tá igual. Eu tenho aqui a raiz cúbica de 6 x√ quad 3. Vai perguntar, pô, como que eu lido com isso? Tá bom? Resposta, você precisa colocar no mesmo índice. Se você não colocar no mesmo índice, o negócio fica incomunicável, tá? Aí vai falar: "Meu Deus, mas ã como é que eu posso colocar essas raízes do mesmo índice, né? Porque o índice de uma delas é três e o índice de
outras dela, da outra delas é dois. Bicho, você vai ter que ter aqui um raciocínio de mmc. Vai ter que ter raciocínio de mmc. Aí vocês vão ver que tudo que eu tô tô ensinando mesmo no ciclo de nivelamento tá muito muito muito consistente, tá bom? Por exemplo, como é que eu faço para essas frações, para essas eh para essas esses radicais aqui chegarem ao mesmo índice? Primeira coisa, eu preciso saber qual é o índice que eu quero chegar. Por exemplo, qual é o índice? E detalhe, eu não quero ficar multiplicando muito isso aqui. Eu
quero saber qual é o menor múltiplo comum entre o índice trê e o índice dois, que é o seis, no caso. Então assim, eu já sei que eu consigo fazer com que as duas tenham o índice seis. É só assim, a poderia fazer outras coisas, mas essa é a forma mais prática de fazer. Eu gostaria que elas tivessem índice seis. Agora pensa em cada uma delas com cuidado, cara. Como você pode fazer, como tu pode fazer para essa Existe alguma forma no mundo de alterar o índice de uma raiz? Vamos pensar em cada uma delas.
Claro que existe. Você pode multiplicar sempre o índice e o expoente eh do radicando pelo mesmo valor. Esse aqui não é um 6 elevado a 1. Eu posso, lembra disso? é uma das primeiras propriedades. Eu falei assim: "Olha, eu posso chegar aqui, se eu tenho aqui radic eh índice n e expoente do radicando m, eu posso multiplicar por x aqui nos dois casos, né? Então, sabendo que o meu alvo, sabendo que o meu desejo é transformar esse índice e esse índice no seis, eu vou fazer o seguinte, nessa primeira, nessa primeira radical aqui, ó, tá
vendo? Eu vou duplicar aqui e aqui. Eu vou duplicar o índice e vou duplicar também o expoente do radicando, que é um, né? Porque não tem nenhum expoente aqui, eu vou dizer que é um, tá? Então, duplica esse cara aqui, raiz se tupla. Duplica esse cara aqui, raiz sexupla de 6 elevado 2. Beleza, tudo certo? Ah, não sei, não tem problema, tá? Esse cara aqui, o teu objetivo é que ele seja seis também. Lembra? Você só consegue fazer multiplicação de radicais quando a gente tem o mesmo índice. Então, esse índice precisa virar um seis também,
tá? Para ele virar um seis, ele tem que ser triplicado. Beleza? Tripliquei. E esse 3 elevado 1 também tem que ser triplicado. Então, 3 elevado 3. E agora? Agora, para tu fazer a multiplicação, você simplesmente repete o índice. Lembra? 6 elevado 6, ó. Eh, perdão, você repete o índice que é seis, né? O raiz sexta continua sendo raiz se tupla. 6 tupla de quem? De 6 elevado 2 x 3 elevado 3. Você só multiplica aqui os radicando os mesmos um pelo outro. Beleza? Quem é agora? Ã, quem é o 6 elevado 2 x o 3
elevado 3? Posso resolver. Posso ficar aqui resolvendo. Então, por exemplo, 6 elevado 2 é 36. Vamos lá. Eu quero a raiz 6 tupla de quem? 6 elevado 2 x 3 elev 3. Então aqui eu tenho 36 x 3 x 3 x 3 x 27, tá? 36 x 27. E eu não tô vendo aqui nenhuma raiz sextuplo aqui fácil para usar. Não tô não tô vendo nenhum número aqui que eu consiga já matar, já resolver, tá? Então fazer o quê, né? Quanto que dá 36 x 27? Ã, vou fazer o 36 x 30, depois eu tiro
108, né? Então 36 x 30 900 1080 1080 - 108 e 972, né? Então tenho aqui, ó, raiz sextupla de 972. Beleza? Ã, agora que eu tenho esse 36, esse 972, não, galera, vocês estão confundindo. Tem gente falando que a resposta do 36 dá para mandar para fora. Não dá, pô. Não tem raiz 6 de 36. Que número vezes ele menos seis vezes vai dar 36, entendeu? Eh, cara, eu não acho que aqui vai ter resposta. Não tem raiz sexta por de 972. Número que vezes ele mesmo. Seis vezes. É o dois, só para ir
testando se o que que eu posso faturar aqui. 2 x 2 x 2 8 16 32 64. Tem aqui dentro algum 64 para pelo menos eu tirar? É, agora deixa eu ver o três. 3 9 27 81 243. É, não tem nada que eu possa fazer aqui. Nada que eu possa fazer aqui. Nada, nada, nada, nada, nada. Isso aqui já é a menor forma possível. Aqui dentro eu não consigo enxergar nenhum número que eu vá, é, por exemplo, eu não, eu sei que aqui dentro eu não vou conseguir e 64 vezes alguma coisa. Se eu
conseguisse 64 vezes alguma coisa, eu tirava pelo menos o 64, a resposta do 64, né? Mas 972, acho que não, 640. Aí do 640 aumenta 332. É, não, não, não tem nada que dê para fazer aqui, tá? É só um exemplo aqui para eu que eu tô mostrando na aula, tá bom? Mas não tem nada que eu consiga fazer nesse cara aqui. Essa é a resposta final, mas eu fiz aqui uma multiplicação de radicais. Beleza? Ã, mais um exemplo. Vamos lá. Então, vou colocar aqui esse exemplo aqui, tá? Raiz cúbica do 4 + raiz tíntopla
do 8. Como que eu lido com isso? Eu precisaria fazer com que eles tivessem aqui o mesmo índice, né, para eu fazer. Eh, mas não, tô viajando aqui, tá bom? Eu ia mostrar a multiplicação, mas eu vou mostrar agora a a divisão, né? Então, olha só, coloca aqui para fazer a divisão, tá? Então, √ quupla do do 8, tá? Para somar, eu já tinha explicado, né? Para somar, você tem que ter total semelhança ali, tá? Eh, nesse exemplo aqui não vai dar para fazer isso. Então, vamos lá fazer essa divisão aqui. Vou mostrar agora a
divisão. Já mostrei com a multiplicação, mas o princípio é o mesmo. Você só vai conseguir executar se você conseguir fazer com que isso aqui, tanto o índice 3 quanto o índice 5 sejam a mesma coisa, tá? Qual é o mmc entre 3 e o 5? É o 15. Então, a melhor coisa que eu poderia fazer é transformar eles dois no 15. Mas como que eu poderia fazer isso? Tá? Vamos lá. Aqui eu sei que tem expoente um e aqui tem expoente um também. Para esse cara virar o 15, ele tem que ser multiplicado por cinco
e aqui dentro também vai ser multiplicado pelo cinco, tá bom? Então aqui eu vou ter raiz de índice 15 do número 4 elevado 5 dividido por raiz. Para esse cara virar índice 15, ele tem que ser triplicado. Então√ índice 15 do 8 elevado 3. Da mesma forma que eu tripliquei ele fora, eu também tripliquei aqui dentro. Então eu posso dizer que isso aqui tudo é raiz de índice 15. Ou seja, que número vezes ele mesmo? 15 vezes vai dar isso aqui, né? que é o 4 elevado 5 dividido pelo 8 elevado 3. Que que eu
posso fazer aqui nesse caso, né, para tentar obter uma melhora na coisa? Eu posso observar o seguinte, galera, só pra gente avançar um pouquinho mais. Tá vendo aqui o quatro e oito? Ã, primeira coisa, não dá para sair dividindo eles, nada disso, não, tá bom? De forma alguma. O que dá para você fazer é individualmente você pegar o quatro e transformar em 2 elevado 2, tá? E individualmente você pegar o oito e transformar em 2 elevado a 3. Tá bom? Então vamos fazer isso. Vamos lá. Eu vou continuar tendo aqui a raiz de de índice
15. Mas tá vendo aqui no lugar do tem 4 elevado a 5. No lugar do 4 eu vou trocar por 2 elevado a 2. Mas lembrando que tudo isso aqui é o quatro que tá dentro do parênteses. 2 elevado 2. E ele tá todo elevado a 5. Tá bom? E no lugar do 8 eu vou botar quem o 8 o8 é. O 8 é 2 elevado 3. Beleza? Então o 8 é 2 elevado 3. Porém tudo que é o 8 que é 2 elevado 3, também tá elevado a 3. Então bota um três aqui fora,
tá? Agora a gente já viu nas outras aulas, né, que a gente multiplica aqui os expoentes nesse caso. Então eu vou ficar aqui com a raiz de índice 15, tá? Índice 15 de 2 elevado 2 elevado 5. Só que eu pego o 2 e multiplico pelo 5 diretamente, tá bom? Então fica 2 elevado 10, OK? E aqui eu vou ter 2 elevado 3, só que tudo isso tá elevado a 3. Eu pego 3 x 3 dá 2 elevado 9. Então 2 elevado 9. Agora sim, eu tô melhorando minha situação. Tô melhorando muito minha situação, porque
aqui dentro eu tenho o quê? uma divisão de potência de mesma base. Isso já tá na aula de potenciação também há muito tempo. Então, como é que eu faço? Eu pego e sub, eu passo o 2 elevado 9 para cima, né, como 2 elevado a -9. Ou eu simplesmente repito a base e subtraio os expoentes. Então isso aqui vai dar o quê? A raiz de índice 15 de quem? De 2. É um número totalmente esquizofrenicamente doido, né? É um número muito doido mesmo. Que número vezes ele mesmo? 15 vezes vai dar o 2. Deve ser
1,00 2, uma coisa louco, louca assim, né? que vai aumentando de pouquinho em pouquinho, umas 15 vezes seguidas vai gerar o dois, tá bom? Mas é essa é a forma simplificada. Isso aqui poderia muito bem chegar eh essa ser a resposta, com toda certeza poderia ser essa a resposta do da prova, numa situação de prova, tá bom? Então alternativa que só tem isso aqui e você tem que fazer essa simplificação. Então pronto, essa aqui foi a aula com todas as propriedades de radiciação, tá bom? Opa, parabéns. Mais uma etapa concluída. Agora a gente vai entrar
em critério de divisibilidade para poder entrar em frações, operações com frações, para depois chegar em MMC, MDC e para depois poder fazer exercícios de Enem vestibulares com essas coisas todas, tá bom? Então você tá mandando muito bem. Continua firme. Fala galera, beleza? Sejam todos bem-vindos mais uma vez a mais uma aula de matemática da plataforma SAD. É um prazer ter vocês aqui. E agora a gente tá aqui no meio do estudo de frações, né? A gente já começou esse esse curso aqui de matemática básica e analisando os números, as casas decimais. a gente aprendeu a
somar e subtrair e aprendeu principalmente a ter um drive mental eficiente. Depois disso, a gente já aprendeu multiplicação e divisão e agora a gente tá no meio de frações. Só que pra gente estudar frações adequadamente, realmente frações é o conteúdo que mais vai exigir requisitos e mais vai exigir didática, tá? Mais vai exigir e malemolência. E se você tiver essas coisas, se você aprender frações muito bem agora, né, que é é justamente para onde eu tô te levando, se você aprender frações muito bem, você vai perceber que a sua inteligência, né, a sua eficiência vai
mudar para sempre, tá? Você vai se tornar um bom aluno em matemática por causa disso aqui, tá? Então agora a gente vai fazer uma pausa no arco normal do nosso conteúdo e a gente vai meio que voltar para um conteúdo que tem a ver com multiplicação e divisão. A gente vai voltar para um conteúdo que tem a ver que lembra o quê? Que lembra o conteúdo de tabuada, tá? Então é um conteúdo mais básico, porém na prática do Enem ele é obrigatório, que são os critérios de divisibilidade, tá? Então você precisa ter a habilidade de
olhar para um número e saber se ele é divisível por outro, tá? Especialmente seria divisível por 2, por 3, por 4, 5, 6, 7, 8, 9, 10, tá? Por exemplo, se você olhar assim o número 17, será que o número 17 é divisível por 10? Você pode falar assim: "Ah, é divisível, dá 1,7, né? Não, mas eu quero dizer divisível perfeitamente, né? Eu tenho 17 pizzas para 10 pessoas. Cada pessoa ganha 1,7 pizza. A pessoa não chega a ganhar duas pizzas, né? Porque aí teria que ter 20 pizzas. Por exemplo, 20 pizzas para 10 pessoas
é perfeitamente divisível, né? 20 para 10. Dá para dividir o 20 pelo 10, tá? E você vai entender como que você faz para enxergar isso mais rápido, enxergar as possibilidades de divisão de um número, tá? 17 não dá. A pessoa, cada um vai receber mais do que uma pizza, mas também não vai chegar a receber duas. Então fica 1.7. Você vai pegar uma pizza e 70% de uma outra. né? Sete fatias das 10 fatias da outra. Então assim, não faz sentido, não é divisível perfeitamente. E a gente vai aprender a fazer isso, tá? Então a
gente vai aprender a pensar, por exemplo, o número três é divisível por dois? Não é, né? Claro que não é. 3 div por 2 vai dar o quê? 1,/ Não, não dá uma divisão exata sem resto, né? O certo é 3 di 2 dá 1 para cada um e sobra um, tá? Como que a gente faz para entender isso? Primeira coisa, como é que a gente avalia se um número é divisível por dois? Basta que ele seja par. Acabou. Todo número par é divisível por dois. Então 1 é divisível por 2, não é porque é
ímpar. 2 é divisível por 2, é 2 por 2 dá exatamente 1, tá? Número 3 é divisível por 2, não é porque é um número ímpar, tá? Então quem são os números que são divisíveis por dois? São aqueles que terminam em zero, em dois, em quatro, em seis ou em oito. Ele tem que ter terminar, né? O último algarismo dele tem que ser esse. Então se for assim 321 é divisível por 2? não é divisível por dois porque não é par, simplesmente porque termina em um. Então o número ímpar, tá? Então o o par é
isso, par vai de dois em dois. O que que é um par? São duas coisas. Então os números pares também são assim, tá bom? Então um número que termina em zero é par, tá? Porque o número 10, por exemplo, ele é par, termina em zero, né? O 11 é ímpar, né? E o 9 também é ímpar. Aí o 10 é par e o 11 é ímpar de novo. O 12 é par e o tr. Então esse aqui é divisível por dois. Esse aqui é divisível por dois, tá bom? Porque é par. Ou seja, basta que
seja par e ele vai ser divisível por dois. A gente já marcou ali, então, que a gente entendeu qual, se você vê um número que ele é parque, ele termina com 0, 2, 4, 6 ou 8, dá para dividir ele por dois de modo exato sempre, tá? Então, se você vê assim, 484 é divisível por 2, é porque termina com 4, é um número par, tá? Quanto que dá isso, né? Dá 242. Pronto, 242, tá? Eu dividi o 400 por 2, que deu 200, o 80 deu 40 e o 4 deu 2. Aí deu 242,
tá? Mas depois a gente fala mais disso. Isso aqui agora é muito importante. Como é que eu faço para saber se um número é divisível por três? Eu preciso somar os algarismos dele. E essa soma tem que ser divisível por três. Você vai falar assim: "Como assim, né? Vamos supor, eu tenho aqui 27. 27 é divisível por 3 de modo certinho? É porque se eu somar os algarismos dele, que é o 2 e o 7, quanto que dá 2 + 7? Dá 9. E o 9 é divisível por 3. Conseguiu entender? Então esse é o
macete, né? Claro que a gente sabe que o 27 é dividido divisível por 3 porque ele tá na tabuada do três, né? 3 6 9 12 15 18 21 24 27 30. Essa é a tabuada do três. Então a gente sabe que o 27 dá para dividir por três e a resposta é 9. Mas e por exemplo, se eu te perguntar assim, ah, vamos fazer 324 dividido por 3? Dá para fazer essa divisão? Dá, porque 3 + 2 dá 5 + 4 dá 9. e 9 é divisível por 3. Então o 324 inteiro também é
divisível por 3, tá? Isso aqui no caso vai dar 108 certinho? A divisão aqui exata, tá bom? 108 sem nenhum problema, tá? Eu dividi de cabeça, né? O 324, eu imaginei que fosse assim, ó. Vou dividir o 300 e o 24 pelo 3, tá? É isso que eu penso. Então, só para já ir contextualizando vocês, né? como é que é o meu raciocínio? Apesar de eu já ensinei um pouco disso, né, nas outras aulas, mas aí eu pego, eh, eu aplico o distributivo, a divisão vai vai pros dois. Então, 300 di por 3 eu sei
que dá 100 e 24 por 3 eu sei que dá 8, dá 108 a resposta. Mas não é sobre isso que é a aula, né? Aqui eu tô apenas mostrando como é que eu faço a divisão aqui na prática, tá? Então, eh, como a gente sabe que um número é divisível por três? Quando a soma dos seus algarismos dá um número divisível por 3, né? Então você tem aqui 1072/ 3. Vai dar para fazer essa divisão certinha? 1 + 0 dá 1 + 7 dá 8 + 2 dá 10. Não dá para dividir por 3.
O 10 não é divisível pelo 3. Então esquece. Esse número aqui todo também não é divisível pelo 3. Se fosse 1071/ 3 aí dá porque 1 + 0 dá 1 + 7 8 + 1 dá 9. 9 é divisível por 3, tá? Se fosse 1074, eu já sei que vai dar para dividir por três, porque 1071 dava. Então agora que eu adicionei mais 3, claro que continua dando, porque eu pulei mais três apenas, né? Então esses três que eu botei vai, né? Vão ser divididos um para cada pessoa. Então aqui 1074, como é que eu
confirmo isso, né? 7 + 4 dá 11. 11 + 1 12. 12 é divisível por 3, porque 12 por 3 dá 4. Então esse número também é divisível por 3, tá? Se eu pensar nele como sendo, vamos dizer assim, o 900 mais o 174, né? Se eu pensar assim, ó, ele aqui vale o 900 + 174, né? É como se fosse isso. E eu vou dividir tudo isso por três. O 900 por 3 eu sei que dá 300. E o 174 por 3 você pensa, cara, se fosse 150 por 3 daria 50. E 24 dá
8, então dá 58, tá? Então 300 + 58 dá 358. 174 por 3 dá 358. Se você fizer o inverso, você confirma. 3 x 8 24/ 2. 3 x 5 15. Com aqueles dois 17 sobra 1. Fica 10.74. Tá? Então você tá vendo como que isso é importante. Isso aqui é fundamental você ter o domínio mesmo completo desses critérios de divisibilidade. Porque você pode olhar para um número e já saber dá para dividir por três ou não dá, né? Então se você ah, 158/ 3, você já sabe se isso aqui vai dar, vai dar certo
ou não vai dar, se vai dar exato no caso, né? Então aqui é 1 + 5 6 + 8 14. 14 não é divisível por 3. Então é claro que até dá para você dividir isso aqui por três, mas não vai dar um número certinho, né? Você vai ter que fazer 158 di por 3. 1 não dá o 15 dá 15 por 3 dá 5. 5 x 3= 15. Até aqui falta 0. Baixo 8. 8 para dividir por 3 tem como? Tem 8 di por 3 dá 2. 2 x 3= 6. Para chegar até 8
falta 2. Agora eu baixo mais um zero e boto uma vírgula aqui. 20/ 3 dá 6. 6 x 3 18. Pá. E vai ficar agora dando isso aqui 52,666666. E nunca vai chegar na resposta certa, tá? Nunca vai chegar na resposta ali exata. Você vai ter que se contentar com isso. Você vai ter que falar assim, ó, dá 52,6, né? Mas se você fizer assim, 3 x 52,6, você vai ver que você vai chegar onde? 3 x 6 18, sobra 1, né? 3 x 6 18, sobra 1. 3 x 2, 6, com aquele um, fica
7. E 3 x 5, 15. Tá? Agora você desce uma vírgula, 157,8. Não chegou a 158, né? Então vai ficar ali pertinho, mas não é uma divisão exata, não é uma divisão que você vai ter uma resposta perfeita, tá? Ao contrário, por exemplo, de você ter eh 161/ 3, né? Eh, não, mentira, 161, você vai ter 1 + 6 7 + 1 8 não vai ser divisível por 3, né? Ao contrário de você ter 162 dividido por 3. 7 + 2, 9. 9 é divisível por 3. Então eu sei que vai dar certo. Vou pensar
aqui em 150 + 12, tá? 150 por 3 dá 50 e 12 * 3 dá 4. Então 54 é a resposta aqui. Tá bem? Então, já entendemos também como dividir, como saber que um número é dividido, divisível por três, tá? Na prática, isso vai ajudar muito, mas muito mesmo a gente nas questões do Enem, tá? Você não tem ideia de como vai te ajudar isso aqui. Como a gente faz para saber que um número é divisível por quatro? Tá bom? Vamos supor que a gente tem aqui o número. O que que a gente precisa verificar?
Se os dois últimos algarismos dele são 0 zer, tá? Se os dois últimos algarismos desse número forem zero, zer, ele é divisível por quatro, tá? Todo número que os dois últimos são zer zer ele é divisível por quatro. Então, por exemplo, 100 dá para você dividir 100 por 4 certinho, dá 25, tá? Se eu tiver aqui eh 200, dá para dividir por 4 certinho, tá? Se eu tiver aqui, ó, 12.000 300, pode ter certeza que 12.300 os dois últimos algarismos são 0 zero, então ele é divisível por 4, tá? Vai dar que o 12.000 por
4 vai dar 3.000 e o 300 vai dar 75. Então vai dar 3075 a resposta disso aqui. Vamos confirmar. 3075 x 4. É 20, né? Sobra 2. 4 x 7 28. Com esses dois sobra três agora porque virou 30. 4 x 0. Boto 3 aqui. Então e 4 x 3 12.300. Então, sempre que terminar com zero zero, não importa quantos tem antes, os dois últimos são 0 zero, então é divisível por quatro, tá? Beleza? Tem outra forma também que é se os dois últimos forem divisíveis por quatro, então por exemplo, 12.300 você viu que termina
com 00, então é divisível por 4, tá? Mas se for, por exemplo, 12.000 e 12.328, dá para dividir isso por 4? Você também vai olhar os últimos dois algarismos. E olhando esses últimos dois algaritmos, você vai ver esses últimos dois, tá? São divisíveis por quatro, né? Sem somar eles. Não é que nem no três que você vai somar 2 + 8 dá 10, não. Você vai fazer assim, o 28 em si, dá para dividir 28 por 4, certinho? E você vai ver que dá, né? Porque a tabuada do 4 é essa. 4 8 12 16
20 24 28. 28 por 4 dá 7, inclusive, né? Mas se isso aqui não é para você botar nenhuma resposta, isso aqui é para você saber, olhar o número e falar assim: "Esse número vai ser divisível por quatro". O todo ele, o 12.328 é divisível por quatro. Por quê? Porque os últimos dois algarismos dele, sem somar, só você olhar os últimos dois, eles são divisíveis por quatro. Então, com certeza, todo número é divisível por 4 também, tá bom? Se você tiver ali, ó, 17.390.484 R$ 484, né? Então aqui, ó, R$ 17.390.484. Isso aqui é divisível
por 2? É porque ele termina com o número par. Ele é par, né? Ele próprio é par porque ele termina com 0 2 4 6 ou 8. Então ele é divisível por 2, tá? Ele é divisível por 3. Vamos testar. 4 + 8 12 + 4 16. 16 + 9. 25 + 3= 28. 28 + 7 35 + 1, 36. A soma de todos os algarismos deu 36. E o 36 é divisível por três. O número 36 você consegue dividir por três, né? A tabuada de três vai até o 30, depois vem 33, 36, tá?
Ah, Pito, mas como é que eu vou saber que o 36, eu somei todos os algarismos aqui, todos e deu 36. Como é que eu eu saberia que o 36 é divisível por 3? Vai no 36 e soma os algarismos dele. 3 + 6 dá 9. Então, realmente é, não precisava fazer isso, mas, né? Se você quiser, você também pode somar de novo os algarismos dele. E o 3 + 6 vai dar 9. Então ele é divisível por 3. Então tudo isso aqui também é, porque a soma dá ele, tá beleza? É divisível por três.
Eu não preciso dividir agora, né? Mas se eu quisesse daria exatamente a divisão certa, tá? Se você quiser ver, porque eu acho que pode ser bom para você, eu vou pegar aqui o número inteiro e vou dividir por três. Então um dá para dividir por três, não dá. 17 dá. 17 dá. Não, não chega no 18, mas tem o 15. Então o 17 por 3, vamos pensar no 15 por 3. O 15 por 3 daria 5, tá? 5 x 3 dá 15. E aí falta 2 para voltar pro 17. Agora baixa o próximo, baixa o
o 3, fica 23 por 23 por 3. Dá para dividir. Vamos pensar no 21. Se fosse 21 por 3, seria 7. Então 7 x 3 dá 21. Para chegar até o 23 faltam 2. Agora baixa esse 9 aqui. 29/ 3. Dá para dividir? Dá. Pensa no 27. 27 dá 9. 9 x 3= 27. Falta 2 para chegar até aqui. Baixa esse zero. 20 dá para dividir por 3? Dá. Pensa no 18. Se fosse 18 por 3 daria 6. 6 x 3 18 para chegar até o 20 faltam apenas dois. Desce esse 4 aqui, 24 dá
para dividir por 3, dá certinho. 8 x 3= 24 fica zero. Aqui eu tinha baixado esse cara aqui. Agora baixa o próximo que é 8. 8 dá para dividir por 3. Deixa eu só pegar um pouquinho mais de espaço aqui. 8 dá para dividir por 3? Dá sim. Pensa por exemplo no 6. 8 por 3 dá 2. 2 x 3 dá 6. E aí falta 2 para voltar para cá. Agora baixo o 24 aqui que é o último que faltava. 24 por 3 dá 8. Acabou. 8 x 3= 24 0. Não sobrou ninguém, né? 8
x 24. Para chegar até o 24 não falta nada. Esse é o resultado. Você tem ali 17.390.584. Que número deu isso aqui, ó? Conta três casas, fecha. Conta três casas, fecha. R$ 5.796.828 para cada pessoa, tá? Se você quiser 5 milhões, ó, você quiser aqui, ó, R$ 5.796.828 R$ 828 x 3. Você tem que voltar a ter esse montante todo. Então 3 x 8 24 so 2. 3 x 2 6 bota ali o 8. 3 x 8 24 sobe 2. 3 x 6 18. Com aquilo ali vai ficar 20. Sobe a 2. Vai virar 29.
Guarda 2. 21. Com aqueles dois vai virar 23. Guarda 2. 15. 17. Três casos aqui. Três casos aqui. R$ 17.390.84. Ou seja, a gente conseguiu ver que aquele número inteiro era sim divisível por três. E a gente até fez a divisão, né, só para aquecer um pouco mais aí o nosso cérebro, porque às vezes no Enem você tem sim divisões grandes assim, chatas e complexas de você fazer, tá? E como é que eu vejo se esse mesmo número, lembra? Se esse mesmo número aqui é divisível agora, deixa eu até reescrever ele aqui, ó. A gente
tava trabalhando com esse 17.390.484. Como é que eu vejo se isso aqui é divisível por 4? Eu olho só pros dois últimos algarismos. Eles são divisíveis por quatro, né? E você vai ter que saber que são o 84 é divisível pelo 4. Aí como assim? Pensa na tabora do 4, tá? Você tem ali 4 x 1, 4, né? Aí 4 x 2 8. Tá aí você tem ali, ó, 4 x 10 40. Aí você tem que ter, e se tu tivesse ali 4 x 11, você ia ter 44. Tá? Onde eu quero chegar com isso?
Tá vendo esse 4 x 10? Cara, você pode ver simplesmente dois dois conjuntos disso aqui. Como assim, cara? Se 4 x 10 é 40, você tem que saber que tu pega o 40, bota 40 + 40, dá 80. Isso também tem que ser divisível por 4, né? 80 também é divisível por 4. Porque se um kit de 40 você pode dividir, o que que te impede de ter outro kit de 40 também? Então eu tenho 40 balas. Ah, dá para dividir por quatro? Dá. E se eu tiver 80? Ué, por que que não daria agora?
Porque eu tinha 40, que já tava ali fechado, dividido, todo mundo certinho. Agora eu tenho 80, mas é é só um outro kit de 40. Então, claro que se o 40 é divisível pelo 4, o 80 também é. Inclusive é o 4 x 20 que dá 80. E aí eu vejo que do 80 para eu ter o 88, eu só preciso botar mais dois números quatro. Então não é 4 20 vezes, é 4 22 vezes, né? 4 22 vezes eu botei aqui mais dois números quatro, ou seja, eu botei aqui mais oito no total, tá?
Então por isso que eu olhei aqui é 84, né? Não é nem 88. Então da mesma forma aqui, ó, eu tenho 4 vezes, eu tenho 20 vezes o número 4 dá 80. E para eu ter o 84 eu tenho que ter 21 vezes, né? Então 4 x 21 dá o 84, tá? Então eu consigo perceber que esses dois últimos são divisíveis por quatro, sim. Então todo um número é divisível por 4 de modo exato, com toda certeza, tá? Para fazer essa divisão, se eu quisesse fazer de cabeça na hora da prova, eu só precisaria dividir
por dois duas vezes, né? Porque dividir por 4 é a mesma coisa que dividir por dois e por dois, tá? Eu acho que eu até consigo fazer isso aqui de cabeça agora, né? Vamos dividir por dois e por dois esse número aqui. Como é que eu vou fazer isso? Vou tentar mostrar para vocês aqui o que que é um raciocínio mental, mas eu nem tenho certeza se eu vou conseguir, tá? Eu vou tentar enxergar metade desse número para enxergar de novo metade depois, porque dividir por 4 é isso, é dividir por dois por dois. Então
vamos lá. Metade de primeiro metade de 17 milhões. Cara, 16 milhões a metade é 8. Então 17 milhões a metade é 8 milhões e 500.000. Você entende? Eu tô escrevendo só para você acompanhar, tá? Então 8 milhões 500.000. Isso é a metade de 17 milhões. Mas sem contar isso aqui. Qual é a metade de 390.000? Se fosse metade de 400.000 seria 200.000. De 390 é só 195.000, entendeu? Então tem que botar aqui mais 195.000 que é a metade desses 390.000, tá bom? 190 x 2 dá 380. 5 x 2 dá 10, 390. E a metade
de R$ 484 é R$ 242. Então R$ 242, tá? Então aqui dá R$ 8.500.000, não, R8.695.000 R 695.242. Tá bom? Divide de novo por dois isso aqui. Então como é que divide isso aqui por dois? Metade de 8 milhões, 4 milhões. Metade de de de 600.000. Só de 600.000 300. Então 4.300. Metade de 95 dá 47,5. Então 4 milhões 347 e 500. Aí metade disso aqui dá apenas 121. Então o 500 + o 121 621, tá? Não precisa fazer assim. Eu acho que eu acertei. Beleza? Vou confirmar agora aqui se eu acertei porque eu disse
que 17.390.400 R$ 484 dividido por 4 dá esse número aqui. Então agora eu vou multiplicar esse número por 4 para ver se ele vai voltar a ser quem ele era antes, tá? 4 x 1= 4. 4 x 2= 8 4 x 6 24 so 4 x 7 28 com aqueles dois fecho o 30 4 x 4 16 com aqueles 3 ali, 19 agora sobra um. 4 x 3= 12. Com mais 1 ali, 13. Sobra um de novo. 4 x 4= 16. Com aquele 17.390.484. Perfeitamente certo. Tá bom? Então, a gente ficou fera nesses critérios de
divisibilidade de dois, 3 e 4. E agora vamos para a próxima aula, onde a gente vai pegar todos esses critérios de divisibilidade aqui. Parabéns por você ter assistido mais uma aula da plataforma SAD. Isso é a sua preparação pra medicina ou pro curso que você sonha. Continua aqui comigo que a gente vai junto nessa, tá bom? Tchau tchau. Vamos pra próxima. Então, bora, né? Seja bem-vindo aí de novo a mais uma aula da plataforma SAD. E agora a gente vai simplesmente continuar o nosso trabalho, continuar o nosso estudo de entender quais são os critérios de
divisibilidade para os números naturais, os números normais ali, né, principais. OK? Então, quando que o número é divisível por dois? Quando ele é par. Ou seja, qualquer número que termine o último algarismo, seja 0, 2, 4, 6 ou 8, é divisível por 2, com certeza, tá? Quando ele é divisível por trê? Quando você soma todos os algarismos dele e a soma de todos esses algarismos dá um número divisível por três. Quando que ele é divisível por quatro, tem dois critérios. Ou os dois últimos algarismos são 0 zer ou os dois últimos algarismos são divisíveis por
quatro. Então não é somando os últimos dois, não, tá bom? É os últimos dois formam um número divisível por quatro, tá? Então 736, os últimos dois são divisíveis por quatro, então todo ele também é divisível por quatro. Tá bom? Beleza. E quando que um número é divisível por 5? Simples. Se ele terminar em zero ou em cinco. Simples, tá? Um número só é divisível por cinco se o último algarismo dele for o zero ou cinco, tá? Porque a tabuada de cinco funciona assim, né? Tu vai 0 5 10 15 20 25 30. Certo? Você vai
seguindo dessa forma e todos os números que terminam em cinco ou zero, com certeza, são divisíveis pelo cinco, tá? O cinco não vai formar nenhum outro número, né? Quando você vai pegando, você não vai conseguir ter outro pacote nunca que uma coisa que tá indo de cinco em cinco vai terminar em outra coisa que não seja o cinco ou zero, porque só dá para fazer assim, ó. 5 10 15 20 25 30 sempre terminando com 5 ou com zero. Então é bem fácil de você saber qualquer número que seja terminado em cinco ou zero é
divisível de modo exato pelo cinco, tá? Exato. Não vai sobrar nada, tá? Então 790 milhões e 384.321, né? Isso aqui é divisível por 5? Não, porque o último número é um. Agora, se for 320 é divisível por 5. 325 também é divisível por 5. Exatamente. Tá? Matamos divisível por se é simplesmente você entender o seguinte, tá? O se é feito de quê? O se não é um 2 x 3, tá? Qualquer número para ser divisível por se ele tem que ser ao mesmo tempo divisível por 2 e por três, tá? Ou seja, só é divisível
certinho pelo seis o número que é par e que a soma dos algarismos dá um número divisível por 3, né? Como assim? Como é que você sabe se um número é divisível por se? Ele tem que ser divisível pelo 2 e pelo 3, ao mesmo tempo, pelo 2 e pelo 3, tá? Então, 798 dá para dividir isso aqui exatamente pelo 6? Vamos ver. Ele é, primeira coisa, isso aqui é divisível por 2, é, é par. Então, só de ser par de terminar com oito, com 0 2 4 6 8, eu sei que ele é divisível
por 2, mas eu quero saber se ele é divisível por seis. Ou seja, tem que ser divisível por 2 e por 3. E por três eu tenho que somar os algaritmos. Então, 7 + 9, 16. 16 + 8 24. Opa, 24 é divisível por 3. Ou seja, o 798 é divisível por 6, porque ele é divisível ao mesmo tempo pelo 2 e pelo três. Então, por se também é, tá? Se eu posso separar ele em pacotes, né, para para duas pessoas ou para três pessoas ao mesmo tempo, isso quer dizer que eu também poderia separar
em pacotes para seis pessoas, tá? E aí, tanto que você vai ver que dá mesmo, né? Então 798/ por 6. A gente pode armar aqui bonitinho. 798 dividido por 6. 7 dá para dividir por 6? Dá, dá 1. 6. Falta um para chegar até aqui. Baixo 9. 19 por 6. Vamos pensar no 18. 18 daria 3. 18. Falta 1 aqui. Baixo 8. 18 por 6 dá 133. 3 x 6 18 não falta nada. Então a resposta é essa. 133. Ou seja, certinho, né? Foi dividido por seis ali, sem sobrar resto nenhum, tá? Você sempre vai
avaliar isso, tá bom? Então, se a gente tem aqui, por exemplo, o número 800, 800 dá para dividir por 6? Ué, dá para dividir por 2 e por 3? Por 2 dá, porque termina com zero. Então dá para dividir por dois porque é par. E por 3, 8 + 0 + 0 dá 8. 8 não é divisível por 3. Ou seja, também não vai dar para dividir por 6, porque precisa ser ao mesmo tempo por 2 e por três. Tá bom? Agora, se for 801, ah, agora 801 é divisível por 3, né? 8 + 1,
9, mas não é divisível por 2, então também não dá para dividir pelo 6, tá bom? 802 por 6 dá é par, então é divisível por 2, mas 8 + 6 não dá certo porque dá 10. 10 não é divisível por 3, tá? 803 não é divisível nem por 2 porque não porque é ímpar, né? E também nem por três porque dá 11. 804 é divisível por 2 porque é porque é par e é divisível por 3. Será 8 + 4 dá 12. E 12 é divisível por 3, ou seja, também é divisível por 6,
tá bom? Então 804/ 6 8 por 6 dá 1. 1 x 6 sobra 2 aqui. Falta 2 aqui, né? Então 20 por 6. Pensando 18, 3 x 6 18, sobra 2 aqui, baixo o 4. Dá o próprio 4, tá? Então 4 x 6 dá 24, sobra zero. Então a resposta aqui é 134. Exatamente. Tá bom? Então critério de divisibilidade por seis é que ele seja ao mesmo tempo divisível pelo número do e 3, tá? Ou seja, ele é par e a soma dos algarismos dão um número divisível por três. Aí ele também é por seis,
tá? Por sete, tá? Para saber se um número divisível por sete aí é um pouco mais complexo, tá? Mas você vai olhar pro último algarismo dele, vai dobrar esse último algarismo e vai pegar o restante do número e subtrair esse número que você obteve. Falar: "Porra, como assim, né?" Pensa assim, ó. 731 é divisível por 7. Eu pego o último algarismo, que é o um, e dobro. Então aqui eu vou ter o dois. Guarda isso. O um aqui eu dobrei, ele virou dois. Agora tá vendo esse restante aqui? 73. Faz assim, 73 - 2 vai
dar 71. 71 é divisível por 7, então não é divisível por 7 nada. Entendeu? Vamos lá. 735. Dá para dividir esse número por 7? Pega o último e dobra. Então pega o 5, dobra, virou 10. Agora, tá vendo? 73 faz 73 - 10 vai dar 63. 63 é é divisível por 7. É 63 tá na tabuada do 7, né? 7 x 9 63. Então, ou seja, quer dizer que todo esse número aqui também é divisível pelo sete, tá? Esse número é, eu não faço muito assim, eu olho mais assim, cara. Esse número aqui eu vejo
assim, tem 700 que é divisível pelo 7 e tem o 35 que também tá na tabora do 7. Então ele é 700/ 7 dá 100, 35 por 7 dá 5. Então a resposta aqui é 105, tá? Eu faço assim, né? Mas às vezes você pode achar mais vantajoso fazer de outra forma. Então se você tem aqui, ó, e 83.409 é divisível por 7. pega o último algarismo e dobra. Dá 18. Agora você faz o restante menos isso. Então aqui, ó, tá vendo isso aqui, ó? 8340. 8340 menos o último dobrado, que é 18, né? Vai
dar 8300 e ó, até travei aqui, - 22, né? 832, né? Porque eu tava tirando aqui 40 men 18, né? Fica 22. Isso aqui é divisível por 7. Aí você vai falar: "Porra, Pedro, não sei." Aí você vai ter que vir aqui de novo, pegar o último número desse aqui, pega este último número porque tu quer saber se isso tudo é divisível por sete, né? Então você pega o último número, dobra, vai virar 4. 832 - 4 dá 828. Isso é divisível por 7? Ah, ainda não sei. Pega o último aqui, dobra, dá 16. 82
- 16 dá 72. Eh, 66, tá? 66 é divisível por 7, não é? Então, nada disso aqui é divisível por sete no final das contas. Beleza? Deixa eu pensar aqui num exemplo que seja. Agora, pronto, né? Peguei aqui um exemplo que é parecido com o de cima. Então, 83.384. Como é que eu faço para saber se dá para dividir isso por sete? Pego o último, dobra. Então, quatro, dobrou, virou oito. Agora pego o restante e tira esse oito. O restante é 8338. Então, menos o 8 vai ficar 8330, tá? Isso aqui é divisível por 7.
Você vai falar: "Ainda não sei". Pega o último, dobra. Zero dobrado vai virar zer e 833 menos isso aqui dá o próprio 833. 833 é divisível por 7? Você fala: "Não sei, pego o último, dobra". Então, 3, dobrou, vai virar 6, tá? 83 - 6 dá o quê? 77. Entendeu? Dobrei aqui o último, virou 6. Aí pega 83 men esse 6 dá 77. 77 é divisível por 7, né? que a tabuada do set vai assim e 0 7 21 35 42 49 56 63 77. Tá? Ah, fiquei na dúvida ainda. não tem mais o que
fazer agora, né? Chegou um ponto que você tem que saber, né? Então, mas o que que acontece? Eu tô ensinando isso aqui porque é é certo ensinar isso aqui. É, mas eu não uso isso. Eu tô falando assim, eu uso até aqui 100%, eu uso isso aqui para caramba na hora da prova, né? Uso isso aqui, uso isso aqui e uso isso aqui. O do sete para mim é o mais inútil, é muito trabalho e não vale a pena, tá? Eu não costumo verificar dessa forma, tá? A menos que fosse, sei lá, um número menor,
né? Se fosse, sei lá, 384, né? É divisível por 7, pega esse 4, dobra, vira o 8. Aí 38 - 8 dá 30, não é? Entendeu? Aí 382 dá para dividir por 7, pega o 2, dobra, vira o 4. 38 - 4 34, não é, né? 381 dá para dividir por 7, pega esse dois aqui, dobra, vira 2. 38 - 2, 36, não é divisível por 7, né? 380 e 388, né? Pega esse 8 aqui, dobra ele, vira 16. 38 - 16 dá 22. Também não é divisível pelo 7, tá percebendo? 383, você dobra aqui,
vira 6. 38 - 6, 32, não é divisível pelo 7. Se fosse uma situação dessa, né, em que eu precisasse testar muitos números de modo rápido, eu até aplicaria. Então, a 385 dá para dividir por 7, pego 5, dobra e virou 10. 38 - 10 dá o quê? 28. 28 é divisível por 7. Então, quer dizer, tudo isso aqui também é divisível por 7, porque eu dobrei, virou 10. 38 - 10, 28. 28 é por 7. Então isso aqui tudo também é divisível por 7. Mas por que que eu acabo não fazendo isso, né? Se
me perguntar assim, 385 dá para dividir por 7, eu vou tentar visualizar grupos de sete que eu conheço. Por exemplo, né? Se eu tivesse assim, ó, 147, né? Vamos pegar que eu tivesse aqui, deixa eu fazer um exemplo mais difícil. 154 dá para dividir por 7? Eu ia pensar, mano, pega o 154, visualiza 70. Pensa no número 70. O número 70 já é 10 vezes o 7. Agora pensa no número 140. O número 140 é 20 x 7, né? Então tá vendo esse 154 aqui? Tira dele 140, porque 140 é o quê? É 7 7
vezes. Então o 140 ele é um grupo de sete coisas. Ele é um grupo de de grupos de sete 20 vezes. Mas por que que tu tirou isso, Pedro? Porque eu vou ver o seguinte, que 154 menos esse grupo aqui sobra só 14. Então o seguinte, das 154 balas eu já peguei 140 e distribuí para para sete pessoas. Agora eu pego mais 14 que faltaram e também distribuo. Vai dar duas para cada uma. Então eu faço divisão assim, você tá entendendo? 300 é 154/ 7. Eu penso assim: "Ué, eu vou imaginar aqui 140 + 14
dividido por 7, porque o 140 eu sei que dá 140 por 7 da mesma forma que 70 por 7 é 10, 140 por 7 é 20. Então resposta é 20 e o 14 por 7 é 2. Então dá 22 para cada um, tá? 385 divido por 7 eu vou fazer o quê, cara? O que me vem na cabeça é o 35, né? Porque 7 x 5 35. Então aqui, ó, eu sei que 7 x 5 dá 35. Aí então eu sei que 7 x 50 dá 350. E olha só, tá vendo do 385? Eu meio
que vejo 350 mais o restante, que é 35. O 350 por 7 eu sei que dá 50, porque 35 por 7 é 5. Então 350 por 7 dá 50. guarda. E o 35 por 7 dá o quê? 5. Então, pronto, essa é a resposta. 385 por 7 dá 55, tá? Então, acaba que o do 7 eu acho basicamente não acho muito usual, tá? Então eu não uso muito na minha vida não esse critério de divisibilidade pelo número sete, tá? Por oito, tá? Também é um dos que eu menos uso, tá? Por oito é o seguinte,
os três últimos tem que ser zero, então tem que ser 0 zer, tá? Para ser divisível por oito, os três últimos tem que ser assim para dar certinho divisível por oito, né? 0 0, tá? Não vou ficar usando isso também toda hora. Não acho que é muito usual, né? Mas é claro, se eu tiver aqui, né, 16000, ah, os três últimos são zero, é divisível por 8. Se os dois últimos são zero, é que é divisível por quatro, tá? Assim dá pra gente dividir por quatro, tá? Se a gente ver os três, é porque ele
é divisível por oito, tá? Ou seja, também é divisível por quatro ao mesmo tempo, né? que se tu pode pegar uma coisa e dividir por oito, é só você pegar os oito agora dividir 4, então, né? Tudo que é divisível por 4 também é divisível por dois, mas nem tudo que é por dois é por quatro, tá? Se você consegue dividir 16.000 por 8 certinho, ó, 16.000, isso aqui é importante, né? Vamos pegar um outro número aqui. Vamos pensar assim, ó. Ah, 20.000 dá para dividir por 8? Dá, porque os três últimos são zero. 0
zer. Dá para dividir por 8, tá? Quanto é que dá isso aqui? Divido, dividido por 8. Eu vou dividir por dois três vezes, que eu faço assim, né? Então 20.000 por 2, 10.000 por 2 de novo, 5.000 de novo dá 2.500. Então essa é a resposta, dá 2.500, tá? Para oito pessoas cada uma recebe 2500. Aí eu falo: "Ué, mas isso em vez de dividir para oito, eu quisesse dividir para quatro, né? Quisesse dividir apenas para quatro, né?" Então aqui, ó, eu peguei aqui, ó, 1 2 3 4, né? 5 6 7 8 pessoas e
cada uma delas está o quê? Com 2500, tá? Cada uma delas está com 2.500 ali, né? desse jeito aqui, né? Ah, eu queria ter dividido apenas para quatro pessoas. Que que impede de tu pegar o que os outros quatro receberam e o dele aqui tu dá para ele, o dele você dá para ele, o dele você dá para esse e o dele você dá para esse. Você sempre vai poder fazer isso. Se tu conseguiu dividir para oito pessoas, o que que te impede de pegar essas oito e pedir para cada uma delas duas se juntarem?
Ó, junta de dois em dois aí e junto o que vocês receberam. Faz dupla aí. Aí vai ficar por quatro. E depois que você tiver só quatro pessoas, cada uma recebendo ali 5.000, não é verdade, né? Até porque para dividir por quatro, os últimos dois tem que ser zero. Então aqui os últimos dois são zero. Claro que também vai dar, né? Agora nada te impede de falar assim, ó, juntem de novo em duplas. Então agora você vai dividir por dois. Quando você dividir por dois, vai dar 10.000 para cada um, tá? Agora, não é porque
uma coisa pode ser dividida por dois, que ela pode ser dividida por oito, por exemplo. Então aqui, ó, e 16 dá para dividir por dois, dá, porque é par. Aí dá oito para cada um, dá oito para você e oito para você. Aí agora eu quero dividir para quatro pessoas, né? O 16 eu quero dividir para quatro pessoas. Por coincidência dá, mas nem sempre dá, né? Nem sempre dá. Então, por exemplo, ó, 14, dá para dividir 14 por 2, dá. Dá sete para cada um. Ah, e dá agora para dividir o 14 por 4? Não
dá, porque cada uma recebeu sete. Agora tu vai ter que pedir para elas darem o quê? dividi o sete delas em 3,5. É claro que 14 di por 4 a resposta é 3,5, mas não é uma divisão exata. E esses critérios aqui é pra gente encontrar as divisões exatas, tá? Outra forma de você verificar que o número é divisível por oito é que os três últimos sejam zero ou que os três últimos sejam divisíveis por oito, né? Então, se você tiver um número que o os três últimos dele são divisíveis por oito, né? Então, vamos
supor, você tem ali é 74.000 1 320, né? Os três últimos são 0, não, mas os três últimos são 320. O 320 é divisível por 8, tá? Então tudo isso aqui também é divisível por oito, tá? Mas enfim, não é muito muito útil também. O de o de sete, o de oito eu não acho muito úteis, mas é bom você ter por nove. Eu acho bem útil, tá? Como é que você sabe que dá para dividir algo por nove? É muito parecido com o do três. Como é que é o do três? Você soma os
algarismos e vê se eles são divisíveis por três. Divisível por nove? Não, você somos algarismos também, mas vê se eles são divisíveis por 9 em vez de por três, né? É super intuitivo. Então, se você tem assim, ó, 830 4, né? Isso é divisível por 3. Vamos somar os algarismos. 8 + 3, 11 + 4, 15. É divisível por 3. Top. Porque 15 é divisível por 3. A soma deu 15. 15 por 3 dá certo, né? Agora é divisível por 9. Vamos somar os algarismos. 8 + 3, 11. + 4 15. Só que o 15
não é divisível por 9. O 15 é divisível por 3, mas não é por 9. Tá? Agora, se você tem aqui 837, isso é divisível por 3? Será que é 8 + 3? 11 + 7 18. 18 é divisível por 3. Ótimo. Então é. Agora isso é divisível por 9 também. 8 + 3 11. 11 + 7 18. O 18 é divisível por 9. Então todo esse número é 18 por 9 dá 2. Todo esse número também é divisível por 9. Olha que top. Tá? Então, eh, eh, se você pensar assim, ah, eh, 12.721, isso
é divisível por 3? Som os algarismos, né? E vê se dá, dá para dividir por três. Então, 1 + 2, 3 + 7, 10 + 2, 12, 13. Não é divisível por 3, né? Claro que não, porque 13 não é divisível por 3, tá? Agora, se fosse aqui 12.723. Soma aqui agora os algarismos. 1 + 2, 3 + 7, 10 + 2, 12 + 3, 15. Opa! E o 15 é divisível pelo 3, mas não vai ser divisível por 9, porque a soma dá 15, né? Agora, se a soma desce, por exemplo, se a soma
desce, deixa eu ver aqui, tem é reduzir seis casos aqui. Então, se fosse assim, ó, 12.717, 717 dá para dividir por 9, ó. 1 + 2, 3 + 7, 10 + 1, 11 + 7, 18. 18 é divisível por 9. Tá percebendo? Então, todo esse número também é divisível por 9. Tá bom? Agora, claro que para dividir por 9, se você quer realmente dividir, você pode dividir por 3 x 3, tá? Porque dá no mesmo. 3 x 3 é a mesma coisa que 9. Então, se eu quiser, eu posso dividir isso aqui por três e
por três, eu vou chegar na resposta, tá bom? Agora, se eu for dividir mesmo 12.717 dividido por 9, 12, 1 não dá, né? Então 12 dá para dividir por 9? Dá, dá 1. 1 x 9, 9 até 12, falta 3. Agora o 7 eu vou baixar aqui. 37 dá para dividir por 9? Dá, pensa no 36, né? 36 por 9 daria 4. 36. Falta 1 para voltar aqui. Baixa um. Agora aqui 11 por 9 dá, dá 1. Dá 9. Até 11 falta 2. Agora baixa o 7. 27 por 9 dá 3. Certinho? 3 x 9
27, falta zero para voltar a ser 27, fecha a conta. Então não tem mais ninguém para baixar, né? Então 12.717/ 9 dá 1413 para cada pessoa, tá bom? Então com certeza 1413 x 9 tem que voltar a ser aquilo. 9 x 3 27 guarda 2. 9 x 1 9 agora fica 11. Guarda 1. 9 x 9 x 4 36 com aquele 1, 37. Guarda 3. 9 x 1 9 com aquele 3 ali, 12. 12.717, assim como estava aqui. Beleza? Esse é o critério de divisibilidade por nove. Você tem que somar os algarismos e eles têm
que ser divisíveis pelo próprio nove, tá? E no três é pelo próprio três. E agora que que vem agora por 10? Qual é o critério para o número ser divisível por 10? É simplesmente que ele termina em zero. Pronto, terminou em zero, é divisível por 10. Tá bom? Então e 791 é divisível por 10? Não. 793? Não. 95? Não. 790 é divisível por 10? É. 790 por 10 dá 79. Deu para pegar? É só isso, tá? terminou em zero, o último número é zer, o último algarismo tem que ser zero, só isso. Aí ele vai
ser divisível por 10. Beleza? Espero que você tenha gostado dessa aula, que tenha sido uma coisa engrandecedora pra sua inteligência, tá bom? Porque esse é o objetivo e a gente tá apenas começando, tá? Parabéns por mais uma aula assistida, mais uma conquista que você realiza na sua vida e vamos pra próxima. Ruma ao seu sonho e eu tô junto contigo. Tchau, tchau. A gente vai seguir, tá? E a gente vai pegar aqui agora com foco nisso aqui, as habilidades fundamentais de frações. E depois a gente vai finalizar aprendendo a fazer as operações com frações. Mesmo
que você já saiba, é importantíssimo que você permaneça aqui e fique junto comigo, tá? Porque o que eu vou ensinar aqui vai deixar a sua visão mais rápida. Então eu não vou apenas te ensinar frações, eu vou te acelerar em frações, tá? Então o seguinte, a primeira habilidade fundamental que a gente vai aprender é entender o que que são frações equivalentes. É muito simples de entender quando você para para pensar nessa fração aqui, ó. 2/3. O que que você tá querendo dizer com 2/3? Vamos supor que a gente tem aqui um círculo, né? Vamos colocar
como se fosse uma pizza representando aqui eh essa fração. Eu quero que você imagine que houve aqui uma divisão em três partes, tá? Dessa estrutura aqui. Então isso aqui é uma parte, isso aqui é outra parte e essa aqui é a terceira. O que que significa a primeira fração 2/3? quer dizer o seguinte, tem uma coisa que foi dividida em três partes, mas dessas três partes eu só tô interessado em pegar duas, entendeu? Então é 2 sobre 3, é 2 a cada três, né? Então uma duas. Isso aqui seria a representação de 2/3. Mas eu
quero agora que você pare para pensar no que significaria a fração 4/6, tá? A fração 4/6 seria o quê? Supondo que eu tivesse ali um círculo semelhante a esse aqui, né? Esse círculo seria dividido dessa vez em seis partes, né? Como é que a gente divide aqui um círculo em seis partes, né? Deixando ele bonitinho. Eu acho que é assim, né? Ó, tá, está aceitável. Embora as partes não estejam iguais, eu quero que você entenda que aqui tem 1 2 3 4 5 seis partes, tá bom? E dessas seis partes, o que que é 4/6?
Quer dizer, eu só quero quatro dessas seis partes. Então aqui eu quero uma, duas, 3, quatro. Tá? Agora, né? Isso aqui é representação gráfica, mas eu quero que você entenda o seguinte, essas frações aqui, elas são a mesma coisa. Elas são o que a gente chama de frações equivalentes, tá? Então eu vou até escrever aqui embaixo para essa essa expressão ficar na sua imaginação. São frações equivalentes. Por quê? Porque elas valem equivalentes, elas valem a mesma coisa, tá? Então, se eu tenho três coisas, eu escolho pegar duas, isso é a mesma coisa do que eu
ter seis coisas e escolher pegar quatro, tá? A gente tem que lembrar o seguinte, tá? Não necessariamente são três coisas ou seis coisas. Não necessariamente, né? O que que eu quero dizer? Eu falar assim, ó, eu peguei 2/3 dessa pizza. Você consegue entender, né? Eu peguei isso aqui mais isso, peguei 2/3, né? Então, eh, dela dividido em três, eu peguei aqui esses 2/3. Mas, né, isso não quer dizer, por exemplo, eu não posso ter o número 100. Eu tenho ali o número 100. Eu falo assim, quanto é 2/3 de 100, né? Quanto é 2/3 de
100? Ou seja, eu sei que se eu tivesse três partes, eu ia querer só duas, mas eu não não tenho três partes. Eu tenho 100. Então, tá, a cada três eu quero duas. Mas e se eu tiver 100 partes? Eu vou mostrar de outra forma aqui, né? Quanto é 2/3 de 90, por exemplo, né? Bem, vamos lá. A primeira forma de você fazer isso é você simplesmente multiplicar aqui o que tá em cima pelo que tá em cima e o que tá embaixo pelo que tá embaixo. Sendo que aqui é 90 sobre 1, não tem
nada embaixo. Então quanto é 2/3 de 90? 2 x 90 dá 180. E quanto que é 3 aqui xes 1? É o próprio 3. 180 di 3. Eu sei que o 18/ 3 dá 6. Então o 6 com mais um z0. Então a resposta é 60. Olha que interessante. 2/3 de 90 deu 60. O que que isso quer dizer? Isso quer dizer que se eu pegasse um círculo e dividisse esse círculo em 90 pedaços, eu quero que você imagine eu dividindo ele em 90 pedaços. É muito pedaço, né? Vai ter que dividir ele várias vezes.
Mas 2/3, da mesma forma que se tivesse três pedaços, eu ia querer só dois. Se tiverem 90 pedaços, eu quero 60. Eu quero que você entenda que é a mesma coisa, tá? Que a gente tá falando aqui da mesma proporção, né? Então, por exemplo, e eu tinha ali, eu peguei duas coisas, o quê? Duas coisas de três. Mas e se eu quiser pegar a mesma pizza? É a mesma, galera, é a mesma pizza aqui e aqui. Eu não sei se você percebeu. Só que agora eu falei assim: "Ah, eu vou cortar em seis fatias". Mas
antes eu tinha comido de três fatias, eu comi duas. Então agora de seis fatias eu vou comer quantas? Eu vou comer quatro. Eu dobrei aqui, é o dobro do número de fatias, então eu vou comer também o dobro de pedaços, o dobro de fatias, tá? Mas é d vale lembrar que é a mesma pizza, tá? Ou seja, 2/3 vale alguma coisa por si só vale, né? Quanto que é 2/3? Quanto é 2 di por 3? Dá mais ou menos 0,66, tá? E 0,66 significa o quê? 66% de alguma coisa. Então, 2/3 vale isso. O número
2/3, a fração 2/3 vale 0,66. Mas ela também, se eu perguntar quanto é 2/3 de alguma coisa, eu sempre vou tá querendo imaginar que essa coisa foi dividida em três pedaços e desses três eu só quero dois. Agora, de quanto são esses três pedaços? Aí depende da coisa. Por exemplo, quanto é 2/3 de 90? O que que você tem que entender aqui? Quando eu pergunto para você quanto é 2/3 de 90, eu quero que você imagine o número 90 sendo dividido em três partes. Uma parte de 30, outra de 30 e uma de 30, não
é verdade? Faz total sentido que o número 90 seja dividido desse jeito, né? Três partes. E o que que eu quero, né? O que que eu quero? Eu quero 2/3. Então, eu quero essa parte mais essa parte que dá 60. Por isso que 2/3 de 90 é igual a 60, como a gente comprovou aqui. E a gente poderia comprovar isso de várias maneiras, tá? Então, se eu tenho uma coisa dividida em três pedaços, eu quero dois. Mas e se ela tiver em seis? Eu vou querer quatro. E se eu dividir em 12 pedaços? Se eu
dividir em 12 pedaços, é o dobro disso aqui. Então, aqui também vai acompanhar, vai ser o dobro. Se eu tivesse 12 pedaços, eu comeria oito pedaços. Se eu tivesse aqui esse mesmo círculo, mas dessa vez dividido em 12 pedaços, eu comeria oito. Ó, vamos ver se vai dar certo aqui, ó. Aqui a gente já tem 1 2 3 4 5 6 7 8 pedaços, né? Agora apareceram mais dois. Não vai ficar simétrico, né? Mas aqui tem 12 pedaços. Desses 12 pedaços, eu quero 1 2 3 4 5 6 7 8 e sobraram quatro. Isso aí.
Isso é a mesma coisa que dizer que eu pintei 2/3 dessa pizza, tá? Como é que eu sei disso? Me diz uma coisa. Em quantos pedaços ela foi dividida? Conta. 1 2 3 4 5 Você vai achar 12. Foi dividido em 12 pedaços. E desses 12, quantos você quis? 1 2 3 4 5 6 7 8. Você quis 8. Ah, Pedro, deu 8/bre 12, não deu 2/ 3. Simplifica essa fração. Tá vendo esse 8/ 12? Ah, eu comi 8/bre 12. Você fala 8 12 avos, tá? Você fala assim, ó. 8 12 avos da pizza. avos.
É para você dar o nome aqui pro que tá aqui embaixo, tá? Então comi 8 12 avos. Mas que fração é essa? Ah, é 8/ 12. Tá bom. Mas 8/bre 12 eu tô te dizendo que é a mesma coisa que 2/3. Você tem que imaginar que se o 12 tivesse dividido, ó, em 4, né? Tá dividido em 3, 4, oito seria isso aqui. Seria 2/3 da mesma forma. Tá começando a compreender? Tá vindo, tá vendo a conexão, mas como é que você visualiza isso aqui como 2/3? Você simplifica. O que que é simplificar? divide em
cima e embaixo pelo mesmo número, que os dois possam ser divididos. Então, como assim? Eh, 8 e 12, eles podem ser divididos por dois. Você concorda? Divide por dois, ó. Dividiu por dois, fica 4. Dividiu por dois, fica 6. Agora divide por dois de novo. Então, dividiu por dois aqui, fica 2. Dividiu por dois aqui, fica três. Pronto, 2/3. Essa é a forma irredutível da fração. Não dá para dividir mais aqui, porque não dá para dividir por dois e por três ao mesmo tempo, né? Não dá, tem que fazer a mesma coisa em cima e
embaixo. Não dá. ou é dois ou é três. Então essa é a menor forma possível dessa fração. Mas qual que é o ponto principal aqui de você perceber? É você perceber que 2/3, 4/6 e 8/1/1 são frações equivalentes. Por quê? Elas têm o mesmo valor, elas representam a mesma fatia, elas representam a mesma proporção. Entendeu? se o cara vai comer um sobre do pizza ou se o cara vai comer 2/4 ou se o cara vai comer 4/8 da pizza. Isso aqui é indiferente no sentido de qual é a parte que ele tá comendo da pizza.
Ele tá comendo sempre a mesma parte, tá? Eu vou provar isso para você agora, ó. Então aqui, ó, botei esse aqui, botei esse aqui. Tá vendo? Tô ficando mais dinâmico, ó. E aí, olha só, se eu tô falando que o cara vai comer meia pizza, né? Eu tô dizendo que ele vai comer o quê? Que ele vai comer meia pizza. Ou seja, se ela for dividida em dois pedaços, ele vai querer um desses dois pedaços. Vai comer meia pizza, né? Vai comer 50% da pizza. Se eu falar que ele vai comer 2/4, quer dizer o
quê? Se essa pizza for dividida em quatro pedaços, ele vai querer dois pedaços. Então agora tá dividindo em quatro. Tá dividindo em duas vezes mais, mas ele vai querer duas vezes mais pedaços também. Mas a quantidade de pizza é a mesma. Ele vai querer um pedaço e outro pedaço. Ele vai querer dois a cada quatro. Ele vai estar comendo 50% da pizza. Vale a mesma coisa, né? Então 1/2 e 2/4 vale a mesma coisa. São equivalentes. É isso mesmo. E se a pizza for dividida em oito, ele vai comer o quê? Ele vai comer a
mesma coisa de sempre, tá? Se ela for dividida em oito, ele vai comer quatro. Ah, quatro fatias não é mais não. Que quatro fatias, quando as fatias estão divididas em oito, dá a mesma coisa, ó. 1 2 3 4. Pronto. Tá comendo o quê? Novamente metade da pizza. Tá bom? Se você simplificar aqui o 4 e 8, divide o 4 por 4 dá 1, o 8 por 4 dá 2. Divide o 2 por 2 dá 1 e o 4 por 2 dá 2. Então tudo isso aqui é sempre meio, tá? Então isso são frações equivalentes,
beleza? Então vou vou te mostrar como é que você gera essas frações equivalentes, né? Como é que eu consigo fazer isso? Se eu tô aqui com a fração 3/4, como é que eu gero uma fração equivalente a ela? Basta que eu realize a mesma operação em cima e embaixo, né? seja de multiplicação ou de divisão, tá? Então, nesse caso aqui, não dá para dividir por nada. Não dá para dividir por três porque aqui não dá, e não dá para dividir por dois porque aqui não dá. Então eu vou, por exemplo, multiplicar para achar outras frações
equivalentes. Eu vou dobrar em cima e vou dobrar embaixo. Pronto, tá dando a mesma coisa, né? Agora eu vou dobrar em cima e vou dobrar embaixo. Então, dobrei em cima, ficou 12. Dobrei embaixo, ficou 16. Beleza? Então, é claro, né? Mais uma vez você vai perceber a mesmíssima dinâmica, tá bom? Se a gente tem ali no início aqui, ó, tô poupando o meu tempo e o seu tempo também. Se a gente tem aqui no início, a pessoa fala: "Vou comer 3/4 da pizza". Quer dizer, se a pizza tá dividida em quatro, ela quer quantos pedaços?
Ela quer três. Então, ela quer 1 2 3. Quanto é que é 3/4? Divide o três pelo 4. Ó, para dividir o três pelo 4, a gente vai dividir por 2 e 2. Vai dividir por dois duas vezes, tá bom? Então, 3 di 2 dá 1,5. Dividido por dois novamente dá 0.75, tá? Então isso é 0.75, que é você comer 75% da pizza, ok? Se a pizza for dividida em oito pedaços, ah, eu quero que essa pizza aqui seja dividida em oito, beleza? Só que desses oito o cara vai comer seis. Então aqui, ó, 1
2 3 4 5 6. Adivinha só? Ele tá comendo novamente 75% da pizza. E se ela for dividida em 12? E aqui ela tá 1 2 3 4 tá em oito, né? Então para ela ser dividida em 12, eu vou passar um aqui e vou passar um aqui. Pronto. Agora ela deve est em 12. Mas tá é em 16, né? Então tem que passar um para cá, tem que passar um para cá. Agora deve est em 16. Desses 16, o cara quer comer 12, né? Então aqui, ó, 1 2 3 4 5 6 7 8
9 10 11 12 e sobraram quatro sem comer. Ele comeu 12 de 16. Ele está comendo 75% da pizza também. Tá bom? As 16 fatias elas poderiam ser divididas em grupos de quatro, quatro quatro e quatro fatias, por exemplo, né? E ele escolheu comer quantas? Ele escolheu comer esses quatro, esses quatro e esses quatro. Ou seja, ele escolheu comer 12 de 16. Mas nota que ele tá comendo o quê? 3/4, né? Ele tá comendo aqui da pegou as 16 fatias, você pode dividir elas nesses 4/4 e ele só quer 3/4, que é 12. sobre 16,
tá bom? Que aí vai ter esse restante aqui que ele não vai comer. Isso são frações equivalentes, tá bom? Se você for simplificar aqui, você divide por por divide por quatro em cima e embaixo, né? 12/ 4 dá 3 e 16/ 4 dá 4. Pronto, 3/4 é a forma irredutível e todas essas aqui são frações equivalentes, tá bom? Espero que você tenha gostado da aula, tá? O intuito aqui foi apresentar você a essa noção de frações equivalentes e mostrar essas porcentagens, esses desenhos, porque isso vai integrar sua imaginação e na hora da prova vai fazer
total diferença. Beleza? Até a próxima, então. Tchau, tchau. Opa, seja muito bem-vindo novamente à plataforma SADE. Vamos agora continuar o nosso estudo de frações, certo? Então aqui a gente vai aprender uma nova habilidade, tá? a gente já matou eh essa habilidade de entender o que que são frações equivalentes. Agora a gente vai aprender a comparar frações. Ou seja, a fração ela sempre, no fundo, ela representa um número, né? É claro que quando eu falo meio, 1 sobre 2, né? Quando eu falo 1 sobre 2, d alguma coisa. 1/ 2 de 140, eu tô me referindo
ao 70, né? Meio de 140, né? Metade do 140. Então essa fração aqui tá dividindo esse número dá 70. Mas quando eu falo simplesmente, ah, mas quanto vale meio? Numericamente falando, 1 / 2 vale 0,5. E eu tenho que ter a habilidade de comparar frações diferentes entre si. Então, por exemplo, se eu te der todas essas frações aqui isoladamente, tá? Não é isso aqui de nada, não. H 5/2 5/ 2, perdão, de alguma coisa. Não, não é isso. Não é isso. É, eu tô falando aqui justamente de você comparar isso com isso, com isso, com
isso, com isso e ver dessas cinco qual delas é o maior número. É claro que a primeiríssima forma não é para você fazer assim, mas só tô dizendo assim, a forma teoricamente, o que tem que fazer aqui teoricamente mesmo é você executar a operação 5 di. Quanto que dá 5 dividido por 2? 5 dá para dividir por 2? Dá. Cabe quantos? Cinco. Eh, cabe quantos dois aqui dentro do cinco, né? Cabe dois. Então 2 x 2 4. Falta 1 para chegar até aqui. Eu baixo aqui esse. Eu baixo aqui esse zero, boto aqui uma vírgula.
10/ 2 dá 5, dá 2,5, né? 5/ 2 dá 2,5. Então o número real que tá sendo representado aqui é esse. É o 2,5. E aqui 3/ 6. Cara, você tem que ter essa sensibilidade de perceber que isso aqui é meio, é metade, tá? Quando eu tenho 1 sobre 2, eu sei que é metade. Por quê? O de cima é metade do de baixo. 1 é metade de dois. Então eu sei que essa fração aqui é metade. Essa aqui também é, né? Se eu dividisse em cima e embaixo pelo número três, por exemplo, porque você
concorda que 3 é divisível por 3 e 6 também é divisível por 3. Então se eu dividisse 3 por 3 dá 1 e 6 por 3 dá 2. Então você vê que realmente é meio, tá? Então isso aqui vale meio. Ou seja, tu já vê que essa aqui é bem menor do que essa, né? 3/6 vale apenas e 5/ 2 vale 2,5. Então assim, aqui eu tenho uma coisa cinco vezes maior, porque, né, eu teria que juntar isso aqui para chegar nisso aqui, né? Eu teria que multiplicar essa fração por cinco para chegar nessa. Vamos
fazer esse teste. Vamos pegar aqui essa fração, ó, 3/ 6 e vamos multiplicar ela por 5 aqui, ó. 5 x 3/ 6. Aqui tem 3/ 6, deu isso valei? Eu tô dizendo que se eu multiplicar 5 x eu vou chegar no 2,5, né? Então, quanto que é 5 x 3/ 6, que é a mesma coisa que isso aqui 5 x 3, 15. E aqui embaixo, né, só teria o 1 x 6, né? Então dá 15/ 6. Ah, Pedro, 15/ 6 não é a mesma coisa do que 2,5, nem do que sobre 5/ 2. Calma, né?
Vamos fazer aqui, por exemplo, 15/ 6 é a mesma coisa, mas talvez eu tenha que que simplificar para eu conseguir perceber. Então, vamos dividir em cima e embaixo por quanto? Por três. Pode ser? Pode. Porque o 15 dá para dividir por três? Dá. A resposta é cinco. E o seis dá para dividir por três? Dá. A resposta é dois. Olha só. 5/ 2 chegou até aqui, tá? Tô só te mostrando algumas coisas aqui, né? Tô deixando você mais rápido. E 4/ 5, quanto vale isso? O certo mesmo era fazer 4/ 5, né? 4 dá para
dividir por 5? Não dá. Então tem que botar aqui um zero e um zero aqui com uma vírgula. 40 por 5 dá 8. Pronto, a resposta é 0,8. Tá? Então 4/ 5 é 0,8. Ou seja, não chega a ser 1. Não chega a ser 1. É muito importante que você perceba isso. Isso aqui passa de um, né? Quando eu tenho qualquer número sobre ele próprio, isso sempre vale 1. Então 3/ 3 é a mesma coisa do que 4 sobre 4, que é a mesma coisa que 5/ 5, que é a mesma coisa do que 79/
79, que é sempre 1, tá? Mas quando eu tenho, isso aqui é muito importante, essa noção que eu vou te passar agora, quando eu tenho o número de cima, o numerador menor do que o denominador, eu tô falando de uma fração que é menor do que um, a resposta dela, tá? Então quando eu tenho aqui 3 sobre 4, aqui em cima é menor. Então isso aqui com certeza não chega a dar um. É 0,75. Não chega a dar um, tá? Não chega a dar um. Agora se eu tenho aqui 7 sobre 8, cara, o numerador
é menor do que o denominador. Não vai chegar a dar 1. É óbvio que não vai dar. Teria que ser pelo menos 8 por 8 para dar 1. 7 por 8 vai dar o quê? 0,87, né? Algo assim. 875, tá? Não vai chegar não. Agora, quando eu tenho um numerador maior do que o denominador, se eu tiver assim 9 sobre 8, com certeza isso dá mais do que um. Com certeza isso aqui vai ficar maior do que 1. Tá bom? Porque 8 por 8 dá 1. Agora se tu tiver 9 para dividir por 8, o
que que vai acontecer? O 8 por 8 dá 1, mas ainda vai ter um aqui para tu dividir, entendeu? Você meio que tá tendo aqui, ó, isso, né? O 8 por 8 dava 1. Mas e esse 1 di 8? Só esse 1 di 8? O 1 di 8 sozinho? ele já dá 0,12 0,135, né? Pequenininho, é tipo, é 0,1 e uns detalhes. Estes detalhes são isso, o 2 e o 5. Então é 0,1, tá? Ou seja, quando eu tinha, né, 8 di por 8, isso dava 1. Agora que eu tenho 9 dividido por 8, isso
vai dar 1,1. Já ficou maior do que 1, porque o numerador está maior do que o denominador. Tá bom? É mais uma noção muito importante que você tem que ter para você comparar frações. E 3/4. O certo mesmo era dividir o 3 pelo 4. 3 dá para dividir por 4? Não. Boto aqui um 0. 30 di por 4 divide por 2 duas vezes dá 15 dá 7,5, né? Mas vamos colocar aqui só o 7. 7 x 4 28. 28 para chegar até 30 ainda faltam dois. Eu baixo mais um zero. 20/ 4 dá 5. 0,75
é a resposta. Beleza? 0,75. Tá percebendo que quando você, se você olhasse só para cá, ó, vou olhar pro 4/5 e por 3/4. Qual das duas é maior? Difícil saber, né? Eu tenho aqui, ó, cinco pedaços e eu vou pegar quatro. Ou eu tenho quatro pedaços e vou pegar três. Complicado. Onde que eu tô comendo mais pizza, né? Você prefere o quê? Essa é a pergunta que eu te faço, né? A gente tem aqui o 4/5 e o 3/4. O que que você prefere? Você prefere, cadê? Aqui, ó. Você tem duas pizzas. A primeira opção
é divide essa pizza em cinco partes. Como é que faz para dividir aqui em cinco partes? Ah, tem que botar aqui um centro comum, né? que é um número ímpar de partes, ó. 1 2 3 4 5. Tem cinco partes. E aqui você vai ter apenas quatro partes. O que que você prefere? É a mesma pizza. Você prefere pegar três pedaços desses quatro ou você prefere dividir a pizza em mais pedaços, em cinco pedaços. E você também pega um pedaço a mais. Mas agora os pedaços são menores, né? Porque uma cinco pedaços, ó, um pedaço
desse aqui não é tão grande quanto um desse aqui, né? Não deveria ser. Talvez o desenho não esteja tão perfeito assim. Agora você vai pegar quatro, ó. 1 2 3 4 pedaços. Então, quatro de uma pizza que foi dividido em cinco ou três de uma pizza que foi dividido em quatro, que são maiores, né? Ou ainda talvez você prefira pegar eh dois pedaços. Talvez você, será que você preferia pegar, por exemplo, deixa eu pensar aqui, será que você preferia pegar eh dois pedaços de uma pizza que foi dividida em cinco, né? Você preferia isso? Pegar
dois pedaços de uma pizza que foi dividido em cinco. Olha que exemplo bom. Você de cara já vai dizer que não, né? Você de cara a primeira coisa que você vai dizer que isso aqui você não quer. Sabe por que que você sabe que não? Porque você consegue comparar esse com esse. Porque eles estão tem o mesmo denominador. Então quando você tem e o mesmo denominador, quando você tem assim, ó, nos dois casos eu dividi em cinco pedaços, mas em um eu vou pegar dois pedaços. Em outro vou pegar quatro. É claro que esse aqui
não é o melhor, né? É claro que aqui não. Não é. Agora o problema vem aqui. O problema é justamente entender onde você tá comendo mais pizza. E a resposta mesmo é o quê? 4/5 vale 80% da pizza, né? Porque 4/5 vale 0,8. Se você executa a divisão do 4/5, você chega nisso. E 3/ 4 vale 0,75. Ou seja, aqui você tá comendo 80% da pizza, aqui você tá comendo 75% da pizza, tá? Então é importante lembrar, vamos supor que a pizza tenha é 1 kg. As duas pizzas são iguais, então elas tm 1 kg.
Nesse primeiro caso aqui, esse 1 kg foi dividido em cinco pedaços, né? Cinco pedaços de quanto, né? Cada pedaço de 200 g. Então aqui tem 200 g, aqui tem 200 g, aqui tem 200 g, 200 g, 200 g. E aqui esse 1 kg, ele foi dividido em quatro pedaços de 250, 250 g, 250 g e 250. No primeiro caso, você comeu 1 2 3 4 pedaços. você comeu 800 g. No segundo caso, você comeu 1 2 3 pedaços. Você comeu 750 g de pizza. Então, por isso que você tá comendo mais no primeiro caso em
que você pega 4/5 da pizza para você. Beleza? É, eu tô te mostrando aqui como é que é na prática, né? Para que que se usa isso, né? Em que sentido você precisa disso e quanto que é 2/5, tá? Da mesma forma que 2/5, ó, você tem aqui em relação ao 4/5, você sabe que vai ser menor, né? Como é que faz isso? 2 di por 5. Quanto que é 2 divido por 5? Não dá, tem que botar um zero aqui, um zero aqui. E 20 por 5 a gente sabe que é 4. Então pronto,
dá 0,4. Olha só, apenas 40% da pizza, apenas 04 d1, tá? Então tá comendo pouco. Então qual quais são aqui as frações, né? Como é que a gente ordena essas frações? Vamos colocar da menor para maior. Então a menor fração de todas aqui é o quê? É essa aqui, porque ela dá 04, né? Então é o 2/5. Então primeiro a gente tem aqui o 2/5. Depois do vem o quê? O 3/6, ó. O 3, o 3/6 é a segunda menor fração. Depois do 3/6 vem o 3/4. Depois dos 3/4 vem o 4/5. Depois do 4/5
vem o 5 sobre 2. Beleza? Essa é a ordem crescente. A gente tá colocando da menor fração para maior, tá bom? Essa fração de 2/5 vale apenas 04. Essa de 3/6 vale metade, 05. Essa de 3/4 vale quase 1, vale 0,75. Essa de 4/5 chega mais perto de valer 1, ela já vale 08 0,80. Tanto faz. E essa aqui ela passa de um porque o de cima cinco é muito maior que o de baixo. Então assim, 5 por 2, cara, se fosse 4 sobre 2 já quer dizer o seguinte: tu dividiu a pizza em dois,
tem uma pizza de dois pedaços e tu tá comendo quatro. Ou seja, quanto você tá comendo? 4/ 2 é 2. Você tá comendo duas pizzas inteiras, né? Conseguiu ver essa dinâmica, né? Se eu tivesse aqui, ó, 4/ 2, bicho, isso é a mesma coisa que eu te dizer, né? Você tem aqui a pizza e ela vai ser dividida em dois pedaços. Mas desses dois pedaços, tu vai comer um, dois, né? Então tu vai comer dois pedaços, só que tu vai comer quatro, na verdade. Então tu ainda vai comer tã tã, bicho. Isso dá o quê?
4 por 2 dá duas pizzas inteiras, né? Agora, se tu vai comer cinco pedaços, tu ainda vai comer mais um meio, né? Mais uma meia pizza. Então dá duas pizzas e meia que você estará comendo. Beleza? Então essa aqui é a ordem. Ou seja, o que que você está percebendo, né? Para comparar frações, a primeira coisa para você comparar frações é você perceber se elas têm o mesmo denominador. Quando elas tem o mesmo denominador, ah, que que é maior? 3/5, 2/5, 1/5 ou 4/5 ou 5/5 ou 8/5, né? A gente tem que saber fazer isso,
né? Então assim, primeira coisa, se fosse para fazer a divisão, né? 3/ por 5, né? Isso vai dar 0,6. Tá bom? Eu sei isso consigo fazer porque eu não faço desse jeito. Eu vou mostrar como que eu faço. 2/ 5, isso é 04. 1 di por 5 é apenas 02. Beleza? 4/ 5 é 08. Como a gente já tinha visto, 5 por 5 é o 1 inteiro e 8 di 5 é 1,6. Olha isso. É 1 inteiro, né? Mais 0,6, né? 1,6. Vou até deixar assim porque eu vou mostrar uma coisa sobre isso já já.
Beleza? Olha que sensacional, tá? Você consegue agora saber que, na verdade, a menor é essa daqui, mas é óbvio, elas têm aqui os mesmos denominadores, então você não precisaria ter feito a conta. Se tá todo mundo sobre cinco, todo mundo em relação a cinco pedaços, é só ver aqui por cima mesmo, né? Então assim, essa aqui é a menor, depois vem essa, depois vem essa, depois vem essa, depois vem essa, depois vem essa, tá? Essa aqui é a única que vai ser maior do que um porque o número de cima é maior maior do que
o de baixo. Essa aqui vai ser um porque eles são iguais e todas as outras tm um numerador menor do que o denominador. Elas vão ser menores do que 100%, menores do que uma parte inteira, tá bom? Vale lembrar que um é igual a 100%, tá bom? Né? Tem muita gente que ainda não sabe, que ainda não viu o capítulo de porcentagem porque estamos no alfabetização, lógico. Mas só para já deixar avisado isso, né? Que 1 é 100%, tá? Da mesma maneira que 0,5 é 50% e 0,8 é 80% e assim vai. Então essa é
a forma que você tem de comparar frações quando elas têm o mesmo denominador, tá? Quando elas estão com denominadores diferentes, a primeira forma seria você executar as divisões, mas a gente vai ver que essa forma não é uma forma prática, tá? Então a gente tem que tentar igualar os denominadores. A gente vai ter uma próxima aula sobre isso, né? Mas vamos supor que eu tenha assim, ó. Cara, qual fração aqui é maior? Tô com dúvida nisso. Tô com dúvida entre o 2/3, né? Vamos, vamos supor aqui em cima mesmo, ó, nos primeiros exemplos, eu vou
mostrar como que a gente poderia desenvolver os raciocínios sem fazer esses cálculos, né? Se o Enem chega pra gente, ele coloca tudo isso aqui. Eh, a primeira coisa que você poderia fazer é comparar uma com a outra e igualar o denominador. Por exemplo, eu quero que você pense aqui. Entre essas duas aqui, qual das duas é maior, cara? 5 por 2 ou 3? por seis. É claro que você já sabe, porque você tá vendo que o cinco é maior que o próprio dois, então ali tem mais do que um e o três é menor do
que o próprio seis. Então aqui não chega nem a ter uma unidade inteira, né, da pizza, né? Aqui tem mais de uma pizza, né? Mas eu quero supor que você não percebeu isso para te mostrar o método, tá? Você precisaria igualar esses denominadores, né? Aí você para para pensar, bicho, aqui o denominador tá seis. Cara, eu queria que esse dois também fosse um seis. O que que eu tenho que fazer? Você tem que triplicar ele. Concorda? O que tu triplicar aqui, tu triplica em cima também, né? Numa mesma fração. Se você fizer a mesma operação
embaixo e em cima, ela vai continuar sendo a mesma. Ela vai ser uma fração equivalente. Então, tá vendo aqui o 5 sobre 2, né? O que que a gente vai fazer com esse C? Agora que eu tô percebendo, né, que tem uma parte que tá sendo tampada, né? Eu espero que não tenha prejudicado vocês aí alguma coisa assim, né? E deve ter deve ter ficado meio chato, mas também né, não vou eh regravar agora por causa disso que eu acho que tá dando para entender, né? Mas eu espero que não tenha ficado zoado aqui, não
tenha ficado fora do frame, tá? Então o seguinte, 5/ 2 ou 3/ 6, qual das duas é maior? Pega aqui o 5/ 2 e transforma esse denominador de 2 em seis. Você vai ter que triplicar para isso, né? Aqui, ó, tripliquei. Então, em cima você também triplique. Quanto que é o triplo de 5? É 15. Então, 15/ 6. Então, agora, tá vendo aqui o 5/ 2? Ele virou o 15/ 6, que é uma fração equivalente, né? Agora 15/ 6 em relação a 3/ 6, eu te pergunto, qual é maior? Ficou óbvio, né? De seis fatias,
tu só comeu três. E de seis fatias, eu comi 15, né? Então eu comi 6 + 6 + 3 para dar 15, né? Então comi uma pizza inteira, outra pizza inteira e meia pizza. Por isso que 15/ 6 continua dando 2,5, tá? Isso aqui continua dando apenas meio, ok? Então essa é a próxima técnica, né, de comparação de frações, é você simplesmente igualar os denominadores e você vai ter a noção perfeita. Então entre essas duas aqui, eu tenho 4/5 e 3/4. Caramba, né? Se eles tivessem com o mesmo denominador, ficaria bom. Mas olha, nesse caso
como é mais delicado, ó. 4/5 e 3/4. O que que você vai fazer aqui para você igualar esses denominadores, né? Não é tão simples assim quanto parece, ok? Então, 4/5 e 3/4, qual das duas é maior? Porque 4/5 é menor do que 1. Porque aqui tem o 4 e aqui tem o 5, então é menor do que 1. E 3/4 também é menor do que 1. Lembra? É aquele caso em que isso aqui é 0,8 e aqui é 0,75. Você vê que elas representam valores bem próximos. Então é confuso de você comparar isso assim. Você
poderia igualar os denominadores, mas cara, como é que você vai fazer um um cinco virar um quatro ou um quatro virar um cinco? Você percebe que não dá, não tem como, né? Na outra lá, no outro caso, a gente tinha, né, uma fração que tava era 5 sobre 3, né, e a outra era 3 sobre 6. Então você meio que via uma forma do denominador, acho que era 5/ 2, na verdade, né? era 5 sobre 2 e 3 sobre 6. Era isso mesmo. Você via uma forma do 2 e o se conversarem, né? Porque eles
são múltiplos assim, né? Então assim, e o seis ele é um ele é um múltiplo do do então o seis ele é simplesmente três vezes o dois. Então se você pegar o dois e triplicar, ele vira o seis. E aí você triplica aqui, vira o 15, você consegue. Mas e nesse caso aqui em que você não dá para fazer o cinco virar o quatro, nem o quatro virar o cinco, você tem que ver onde eles se encontram, né? Você tem que pensar o seguinte: o que que são múltiplos? Pensa aqui só no cinco. Eu vou
escrever aqui múltiplos aqui pro cinco, tá bom? Tem o cinco, mas tem, por exemplo, o 10, tem o 15, tem o 20. São números que estão na tabuada do cinco, você tá entendendo? Então tem cinco, né? Tem tem o 0, 5, tem o 10, tem o 15, tem o 20, tem o 25, tem o 30, tem o 35, o 40, 45, 50, 55. Por aí vai, né? Agora vamos pegar alguns múltiplos aqui. Vamos falar alguns múltiplos do quatro. Por exemplo, tem o quatro, né? Aí depois vai ter o oito, vai ter o 12, vai ter
o 16. Eu tô só agrupando de quatro em quatro. Tô botando mais quatro, ó. 20, 24, 28, né? 32 e assim vai, né? 44. Tá? Agora, olha que maravilha. O quatro e o cinco, eles não conversam diretamente, mas eles podem se encontrar, né? Porque tem uma hora que dá para eu fazer com que o 5 vire o 20, né? Se eu pegar o 5co e multiplicar por 4, ele vira o 20. Nota que o 4 também pode virar um 20 se eu multiplicar ele por cinco. Tá percebendo? Ou seja, o 20 é um múltiplo do
5 e o 20 também é um múltiplo do 4. Isso aqui é o que a gente chama de MMC. Olha que maravilha. Mínimo. Ó, você vai ver como é que faz um sentido absurdo, né? Aqui de novo eu tô tampando aqui, né? Então vou vou deixar assim para não ter risco de vocês perderem nada, tá? Vou fazer aqui de uma forma mais legal que vocês não percam ali uma parte do quadro, tá? Perdão aí. Então, o que que é o mmc? Olha como é um conceito intuitivo. É o mínimo, o menor de todos. O quê?
Múltiplo. O que que é múltiplo? É um número que tá, vou colocar uma definição assim, é um número que tá na tabuada daquele cara, múltiplo de sete, né? Aí vai ter o 14, o 21, 28, 35, 42, né? mínimo múltiplo comum, porque o mmc é entre qu e 5. Nesse caso, qual é o mínimo múltiplo comum entre o quatro e o cinco? Essa é a pergunta, tá? Ou seja, existem múltiplos em comum. Primeira coisa, você constatar isso, ah, existem múltiplos comuns entre eles dois. Como assim? O 20 é um múltiplo comum eles dois. Você concorda?
Porque o 20 ele é múltiplo tanto do cinco quanto do quatro. Então é comum. E por exemplo, você vai notar que tem uma uma hora que chega aqui o 40. O 40 é um múltiplo do 5, mas o 40 também é um múltiplo do 4. Então aqui, ó, múltiplos comuns. O 40 é um múltiplo comum e o 20 é um múltiplo comum. Mas eu não quero qualquer múltiplo comum, eu quero o mínimo. Eu quero o menor. E o mínimo múltiplo comum entre 4 e 5 é o quê? É 20. O mínimo múltiplo comum entre 4
e 5 é 20. Beleza? A gente vai ter mais aulas aprofundadas sobre mmc, mas por enquanto só vai pegando isso, tá? Mas Pedro, o que que tem a ver isso? O que que tem a ver? que agora eu sei que o mínimo múltiplo comum entre eles é 20. Vou te mostrar o que que tem a ver. Não sei se vocês viram aqui, tá bom? Mas eu sinalizei aqui que o 40 era um múltiplo comum dos dois e o 20 também. Mas o mínimo múltiplo comum é o 20, que é o menor, né? Mas por que
que eu quero isso? Porque isso vai me ajudar com o que que eu faço para comparar esses dois aqui. Por exemplo, o 4/5 eu preciso, eu preciso fazer eles ter o mesmo denominador. Então, qual vai ser o novo denominador deles? Eu quero que os dois, essa fração e essa, ten o denominador 20, tá? Por que que eu quero isso? Porque olha só, como é que eu faço pro 4/5 ter esse denominador de 20. Ó, vou pegar a primeira fração 4/5 e vou fazer ele ter o 20. Eu preciso multiplicar o 5 x 4. Então aqui,
ó, eu peguei aqui o 5, multipliquei por 4 e virou o 20. Agora aqui em cima, eu só tenho que fazer a mesma coisa. Multiplica por 4 também o numerador. E aí vai ficar o quê? 16/ 20. Ou seja, lembra do 4/5? Na verdade, ele é o 16/ 20. É a mesma fração, são frações equivalentes. Agora, lembra do 3/4? O que que eu quero fazer com 3/4? Eu quero que o denominador dele também vire o 20, tá? Então, pro 4 virar o 20, ele tem que ser multiplicado por 5 e não por quatro. Tem que
ser multiplicado por 5. Então, em cima, eu vou ter que fazer o mesmo procedimento. 3 x 5 dá o quê? 15. Então, agora, olha só, 15/ 20. O 3/4 é o 15/ 20. Olha como agora ficou fácil de comparar essas duas frações, né? O 4/5 ele é o 16/20, né? E o 3/4 é o 15/2. Qual das duas é maior? Essa é maior porque de 20 fatias ele come 16. De 20 fatias ele come 15. Beleza? Então é, a gente resultou que essa daqui descobriu que essa daqui é a maior fração, tá bom? Mais uma
forma então de você pensar, de você compreender esse assunto tão importante, tá? Espero que você tenha gostado, ó. Parabéns aí por ter assistido mais uma aula da plataforma SAD, tá bom? Eu te vejo na próxima aqui do lado. Tchau, tchau. Fala, galera. Beleza? Vamos agora começar então mais uma aula aqui do alfabetização de matemática, né, na nossa construção do nosso raciocínio de matemática básica. E a gente agora vai seguir por um outro caminho, tá? Agora a gente vai voltar pro caminho das frações. E a gente vai, você vai perceber que o tema dos critérios de
divisibilidade, né, os temas que a gente vem tratando, eles realmente são obrigatórios pra gente se desenvolver de modo saudável em frações, OK? Então, sem mais delongas, ajeitando aqui o microfone, né? Vamos lá, vamos começar. Então, nessa aula aqui, você simplesmente vai aprender isso, a arte de simplificar frações e conhecimentos sobre frações próprias, impróprias e aparentes, tá bom? Própria, imprópria e aparentes. Não tem nada demais aqui. Isso aqui é um troço que n caído já, né? Cair negócio de própria, imprópria aparente, não é? Isso aqui é só nomenclatura. Isso aqui é matéria do sexto ano, mas
que é necessária para que você se desenvolva em frações, tá? Então isso, isso aqui, por exemplo, a arte de simplificar frações, isso aqui não é nem dizer que cai, isso aqui despenca. Sem isso aqui você tá ferrado, tá? Eu só vou ensinar isso aqui como bônus, o próprio impróprio aparente, mas isso aqui é obrigatório. O que que é você simplificar uma fração? É você, primeira coisa que você tem que botar em mente, você não vai mudar nada na fração. Simplificar uma fração, ela tem que ser a mesma que ela era antes, tá? Então, o que
que é simplificar uma fração? Primeira coisa, o que que você pode fazer com uma fração? Você sempre pode com qualquer fração que você tenha, né? fração. Isso aqui é o numerador, né? Vamos colocar aqui x e aqui é o denominador. Você sempre pode aplicar uma mesma operação em cima e embaixo, tá? Você pode multiplicar em cima e embaixo pelo mesmo número e a fração continua igual. Então, se eu fizer em cima por 4 e embaixo por 4, então fiz assim 4x/ 4y. 4x/ 4y é a mesma coisa do que x sobre so y. É a
mesma coisa, não é nem maior nem maior, é a mesma coisa, tá? Ah, como assim, bicho? Porque se eu tô falando assim, você tem x partes a cada y ou você tem 4x a cada 4y, tu tem a mesma coisa. Tu sempre tá tendo o mesmo número de partes aqui de baixo, né? Deixa eu botar com um número que vai ficar mais fácil. Se eu falar assim, ó, você tá com duas fatias em uma pizza de oito pedaços, né? Aí eu dobro em cima, vira quatro, dobro embaixo, vira 16. ter quatro fatias numa pizza de
16 pedaços. Você tá tendo a mesma parte da pizza que você teria caso você tivesse dois pedaços numa pizza de oito, né? Agora tem o dobro de pedaços, mas tu também tem o dobro de pedaços, né? Então dá no mesmo, né? 2 sobre 8 aqui nesse caso, isso aqui vai dar 0,25, né? 2/ 8 dá 0,25. Dá 1/2 0,25. E 4/ 16 também dá 0,25. Ou seja, nos dois casos você tem 25% da pizza, tá? Ou 0.25 de uma pizza inteira. E se você tivesse pegado aqui 2/ 8 e dividido por dois em cima e
dividido por dois embaixo, 1/4 da pizza também é a mesma coisa, tá? E por que que eu faria isso? Você pergunta. Porque às vezes fica muito mais fácil de resolver qualquer fração, qualquer questão, se você simplificar, tá? Só que existe uma coisa chamada fração irredutível, que é aquela fração que não dá para ser simplificada. Então, vamos começar. O exercício aqui é esse. O exercício aqui é simplifique as frações. Beleza? Então vamos simplificar aqui a fração eh 5/ 8, tá? Não dá para simplificar essa fração, porque para simplificar, fazer uma fração parecer menor, parecer porque ela
não vai ser de fato menor, eu preciso aplicar a mesma divisão em cima e embaixo. Aí eu te pergunto, dá para eu dividir em cima e embaixo por dois? Não dá. O 8 dá para dividir por dois, viraria o 4, mas em cima vai virar o 2,5. Não existe essa fração. Você não pode botar assim, né? Tem que ser números inteiros, tá? Eh, não pode ser 2,5, tem que ser ou dois ou três. Então, dá para dividir por três em cima e embaixo? Não dá. O cinco não dá para dividir por três, nem o 8.
Dá para dividir por quatro em cima e embaixo? Não dá. O 5 não dá e o oito dá. 8 di por 4 dá 2. O problema é que em cima não dá para dividir por quatro, então acabou. Não dá para fazer nada. Dá para dividir por cinco só em cima, embaixo não dá. Ou seja, essa fração aqui, ela é uma fração que está irredutível. Eu não posso fazer nada com ela. Eu posso só dobrar. Se eu quiser ver ela como 10/ 16, eu posso. Mas isso não vai me ajudar em nada, tá? Agora, se ele
te pede assim, classifique essa fração como própria, imprópria ou aparente, galera, fração própria, olha o nome, própria. Quer dizer, a fração normal, é a fração que a parte de cima é menor que a de baixo, porque isso é o normal, né? Eu tenho assim, ó, 2 sobre 5. Isso aqui é uma fração própria, porque isso, a fração, ela originalmente é para isso mesmo, tá? Para mostrar uma quantidade de outra quantidade. Ou seja, a de cima tem que ser menor. Eu tenho dois duas fatias de uma pizza de cinco. Isso é uma fração própria, tá? Agora
falar assim, eu tenho oito fatias de uma pizza de três. o que 8 por 3 eu tô querendo dizer, na verdade que eu tenho 2,66 pizzas, né? Porque 6 por 3 já daria 2 e aí esse 2 por 3 dá 066, tá? Então, ou seja, essa fração aqui ela não é própria porque ela tem a parte de cima maior que a de baixo, então ela é imprópria. É só isso, tá? A própria é a normal, é a que tem a parte de cima pequena e a de baixo grande e a imprópria é o oposto, tá?
Então é isso. Agora, e a aparente? A aparente é quando você pode perfeitamente dividir o de cima pelo de baixo, por exemplo, né? 8/4. Isso aqui é uma fração, né? Isso aqui é uma fração. É, é uma fração, tá? Ai, Pedro, ela é imprópria porque a parte de cima é maior. Você tá certo? Mas a gente não di, nesse caso, a gente não diz que ela é imprópria. Por quê? Oito dá para dividir perfeitamente por quatro, tá? Cuidado, não é dizer que assim, ah, os dois podem ser divididos por dois, né? Eh, não é isso.
Isso aqui quer dizer que dá para simplificar por dois, mas o fato do numerador poder ser dividido pelo denominador é uma fração aparente. Mas o o nome aparente te lembra o quê? Uma coisa falsa, né? Olha, é aparente apenas, mas na verdade não é. E é isso mesmo, porque 8/ 4 tá tá escrito como se fosse uma fração. Mas cara, quanto é 8 dividido por 4? é 2. Então, na verdade, eu tava querendo só dizer isso, mas por que que eu escrevi 8 sobre 4? Não sei. Uma fração aparente, né? Agora, ao contrário daqui, que
quando eu digo assim 2 sobre 5, bicho, se eu dividir 2 por 5, eu vou ter 0,4. Então assim, não dá para dizer isso aqui de outra forma, só dá para dizer 2/5 ou 04. Mas agora aqui 8 sobre 4, bicho, eu poderia simplesmente dizer dois, que é um número inteiro, seria muito mais fácil. Aqui é aparente, aqui é uma fração própria, normal, tá? Então, beleza. Agora vamos lá no nosso treinamento. Simplifica aqui a fração 3/4. Não dá para simplificar, tá bom? Ela tá irredutível, tá? Não, porque não não dá para dividir os dois por
um mesmo número. Eles não têm, vamos começar a usar uma linguagem melhor. Eles não têm divisores em comum. Divisores em comum. Você lembra o que que é um divisor? O que que é um divisor? É um número que consegue dividir aquele outro. Então, quais são os divisores do CO? O um, porque você pode dividir 5 por um e o cinco, você pode dividir 5 por 5, tá? Por isso que ele é um número primo. O número primo, esse ele só pode ser dividido pelo um e por ele próprio, tá? Quais são os divisores do 12?
O 12 tem esses divisores, o 1, o 2, o 3, o 4, o 6 e o próprio 12, tá? Então o 12 por 1, 12 por 2, 6 por 3, 4* 4, 3 por 6, 2 por 12, 1. Dá para dividir o 12 por todos esses, tá? O como é que você faz para simplificar uma fração? Você tem que ver que o numerador e o denominador eles têm divisores em comum. Então, por exemplo, o três ele tem quais divisores em comum? O um e ele próprio. E o quatro tem quais divisores? O um, o dois
e ele próprio, tá? Então assim, é claro que o um, ah, o um é um divisor em comum, mas o um é divisor em comum de todo mundo. Todo mundo pode ser dividido por um, né? Agora o três só posso dividir por três e o quatro por dois e por quatro. Então, assim, não tem divisores em comum aqui. Não dá para eu fazer a mesma coisa em cima e embaixo, tá? Não tem, não tem nada para fazer aqui. Ela é irredutível, tá? Agora, é claro que daria para eu visualizar elas, tipo, triplica em cima, 9,
triplica embaixo, 12, né? 9 sobre 12 é ainda a mesma fração de 3/4, tá? Agora isso aqui é uma fração o quê? Irredutível. E ela é própria, porque em cima é menor do que em baixo, tá bom? Aqui, 3/ 9, como é que eu simplifico essa fração? Ah, dá para simplificar? Dá, porque eles têm divisores em comum. Então, o se pode ser dividido pelo 1, pelo 2, pelo 3 e pelo 6. E o 9? O nove pode ser dividido pelo um, pelo três e por ele próprio. Nove só pode ser dividido por esses, né? Então,
repara que os dois podem ser divididos por três. Então, o três é um divisor em comum. Eu vou eu vou dividir os dois pelo três mesmo. Então, eu vou dividir os dois aqui. Eu vou aplicar a mesma operação de dividir por três em cima e baixo. Então, 6/ 3 dá 2 e 9/ 3 dá 3. Então, 6/9 é a mesma coisa que 2/3. É a mesma coisa, tá? é a mesma fração. E claro que isso aqui é uma fração o quê? Própria, tá? Isso aqui é fração própria porque o numerador é menor do que o
denominador, tá? E isso aqui vale a mesma coisa. 2/3 é a mesma coisa do que 6/9, tá? 7/ 35 dá para simplificar primeiro, ela é própria ou imprópria? Ela é própria. Vou colocar aqui, só vou falar, não vou nem escrever. Ela é própria. O 7 e o 35 possuem por acaso divisores em comum? Possuem. O 7 e o 35 possuem. você consegue perceber a semelhança deles que tem o sete aqui e o 35 tá na tabada do sete. Então você já vai dar para dividir os dois pelo próprio sete, né? Então o seu interesse é
sempre dividir pelo maior cara que dá. Se eu puder dividir os dois por sete, eu faço isso. Então divide em cima por sete, vai ficar um. Divide embaixo por sete, vai ficar cinco. Ou seja, 735 avos, a gente chama isso aqui de tudo que é embaixo, a gente chama de avos, quando for maior que 10, tá bom? Então até 10 é 7/1, depois é 7 11 avos, 7 12 avos, tá? Então, 7/ 35 é a mesma coisa de 1/5. É a mesma coisa, tá? É a mesma coisa, literalmente não tem nenhuma diferença, tá? É o
mesmo número. Eu tenho 7 sobre 35 daquele terreno, eu tenho 1/5, mesma coisa, tá? Eu simplifiquei. E essa é a forma irredutível. Não dá para irredutível é isso. Não tem mais como simplificar isso, OK? E é própria. Claro. 16/ 144. Eu consigo simplificar isso, galera? De cara dá para ver que eu consigo. Por quê? Porque eles têm divisores em comum. Por exemplo, quem é um divisor do 16 e do 144? Obviamente o dois. Tá entendendo agora como que os critérios de divisibilidade ajudam? Você sabe que eles dois são divisíveis por quem? Pelo dois, tá? Por
que que eles são divisíveis pelo dois? Porque eles são pares. Então, pronto. Se os dois são pares já dá para simplificar. Então, Pedro, eu posso dividir por dois em cima e embaixo? Pode. Vamos fazer 16/ 2 dá 8. E 144 por 2, metade de 140 é 70. metade de 4 e 2, então dá 72. Pronto, essa é a resposta. Não, porque eu pedi para você transformar na forma irredutível. E aqui eu ainda posso reduzir. Por exemplo, tem 8,72, eu posso dividir por dois de novo, não posso. Então vou dividir 8 por 2, vai dar o
quê? 4. E 72 por 2 vai dar 36. Agora eu posso pegar essa fração aqui, né? Vou até tirar esse 8 sobre 42. Vou botar para cá por enquanto, tá? Eu posso pegar isso aqui e dividir por dois em cima de novo. Pode. 4 por 2 dá 2 e 36 por 2 dá 18. Pode. Tá irredutível? Não tá. Porque ainda dá para dividir de novo pelo mesmo divisor. 2 * 2 dá 1. 18 por 2 dá 9. Resposta é essa. 1/ 9 é a forma irredutível da fração 16 144. Precisava ter feito isso tudo? Não
precisava. Se você tivesse pegado, pode fazer assim, pode. Mas se você tivesse desde o início pegado um divisor maior, por você pegou dois, né? Mas você podia ter dividido eles por uma coisa maior. Então você podia ter dividido logo por quatro em cima e embaixo. Por quê? Porque os dois são divisíveis por quatro. Como é que eu sei? que 16 é divisível por 4. E lembra como é que a gente sabe se um cara é divisível por quatro? A gente pega os últimos dois números e vê se eles são divisíveis por quatro. 44 é divisível
por 4, porque tem o 40, tem o 44 logo depois. Então eu posso dividir logo por 4. Dá o quê? 4. E 144 por 4 div por 2 e por 2 dá 72 36. Olha só, eu já pulei direto para cá. A invés de pular primeiro para 8/bre 72, eu pulo direto para 4/ 36. Então é mais rápido, tá? Agora, em vez de dividir por dois em cima e embaixo, por que que eu não divido de novo por 4, né? Divide por quatro em cima dá um e por quatro embaixo dá nove. Pronto, fiz só
duas operações. Antes eu tinha dividido por dois, em cima embaixo, depois de novo, de novo, de novo, tá? Então fiz quatro vezes isso. Agora eu fiz só duas porque eu dividi por quatro, por quatro. E eu poderia, inclusive fazer apenas uma. Por quê? Porque esses dois aqui são divisíveis por 16, tá? E os dois são divisíveis por 16 e são divisíveis inclusive pelo oito, tá? Então assim, eh, como é que eu sei que isso aqui é divisível pelo 8? Eu enxergo assim, ó. Pensa que o 144 é 80 + 64, tá? Eu vejo ele como
80 + 64. 80 divisível por 8, 64 também é, tá? Então eu vejo dessa forma, beleza? Então 16/ 8, cara, vai dar 2. E 144/ 8, cara, se fosse analisar o número que eu conheço, né? Tipo 80 + 64. 80 por 8 é 10 e 64 por 8 é 8. Então aqui vai dar 18. E 2/ 18 eu divido por 2 apenas agora, né? Divide em cima por 2 dá 1. Embaixo por 2 dá 9. Tá? E você poderia ter dividido diretamente pelo próprio 16, porque os dois são divisíveis por 16 também. Eu eu consigo
enxergar isso, né? Porque pensa na tabuada do 16. Eu sei que eu nunca te ensinei, claro que eu nunca te ensinei a tabuada do 16, mas pensa comigo, né? Seria 16, 32, 48, 64, 80, 96, 112, 128, 144, depois 160, tá? Então eu tô querendo te mostrar o seguinte, quando eu olho pro 144, eu eu de alguma forma imagino assim, cara, se ele fosse um 160, ele seria divisível por 16, mas ele não é um 160, ele é um 144. Mas bicho, repara que foi tirado 16 para ele virar o 144. Ou seja, o 160
é divisível por 16. Agora, e se tu tirar 16 dele, ele virar o 144? Continua sendo divisível por 16, porque você tirou um bloco de 16. O que sobrou agora são blocos de 16. Antes você tinha 10 blocos, né? 160 por 16 dá 10. Agora você tem 144 por 16, que dá 9, tá? Então quanto que é 16/ 16? 1 e 144 por 16 o próprio 9. Tá? Na prática, Pedro, como é que você faz na prova? Eu tento fazer da forma mais rápida. Então eu vou tentar dividir primeiro logo pelo 4. 16 por 4
dá 4.4* 4 dá 36. Aí aqui eu divido pelo 4 de novo, vai ficar 1 sobre 9, tá? Essa é a forma irredutível. Isso aqui é uma fração própria, tá? 80/ 480. Como é que você pode simplificar isso aqui, cara? Os dois são divisíveis por dois? Vamos lá. Vamos dividir por dois. Vai ficar 40 sobre 240. É divisível por 2 de novo. É. Divide por dois em cima, vai ficar 20. Embaixo vai ficar 120. É divisível por 2 de novo, vai. Divide por 2, vai ficar 10. Divide por 2, vai ficar 60. É divisível por
2 de novo, vai ficar 10, vira 5 e 60 vira 30. É divisível por 2 de novo? Não. O 30 é, mas o 5 não é. Então não dá para dividir por 2. E por 3? O 30 dá, mas o 5 não dá. E por 5? por cinco os dois não, porque o para ser divisível por cinco tem que terminar em cinco, tá? E o cinco termina em cinco e o 30 em cinco ou em zero, né? O 30 termina em zero. Então os dois são divisíveis por cinco. Divide por cinco em cima dá 1.
Divide por cinco embaixo dá seis. Então a resposta, a fração irredutível aqui é 1/6, tá? Mas, pô, fazer de dois em dois assim me deu um trabalho absurdo. Então, eu vou tentar logo achar um cara grande que seja divisor dos dois ao mesmo tempo. Por exemplo, o 10 eu posso dividir por 10 em cima e por 10 embaixo, né? 80 por 10, para dividir por 10, você só corta um zero, volta uma casa. E os dois são divisíveis por 10 porque terminam em zero. E 480 por 10 você corta o zero também. Ou seja, dividindo
por 10 em cima e embaixo, eu já vou direto pro 8 sobre 48. Agora eu posso dividir, por exemplo, por dois, eu posso dividir por quatro, mas eu posso dividir também pelo oito, galera, porque 48 é divisível por 8, lembra? Aí que vem a tabuada. Se tu não, se tu não viu as aulas de taboada, porque você achou que você era o bonzão, a vou ficar vendo tabuada, não. É, é por isso que você não vai passar. Tô falando sério. Acorda pra vida, bicho. Você comprou meu curso é porque você confia em mim. Você tem
que confiar em mim de verdade, tá? Se eu falar que é para estudar tabuada, e eu tô ensinando tabuada, inclusive, é para estudar taboada. Não é você quem sabe o que que você tem que estudar. Se é você quem sabe, então você não precisa de mentor nenhum, tá? Eu sempre escutei os meus mentores, é por isso que eu passei muito rápido, tá? E porque os meus mentores eram bons e eu sou muito bom também, tá? Então, eh, inclusive, eu acho que eu sou o melhor mentor disponível no Brasil atualmente. Então, escuta o que eu tô
falando e segue o que eu tô falando. Não pule nenhuma aula, não, tá? Dividir por 10 em cima e embaixo. Agora eu posso dividir por oito. Então, vou dividir aqui por por 8. Isso aqui vai virar 1 e 48 por 8 vira 6, tá bom? Porque eu sei que 6 x 8 aqui dá 48, tá? Então 48 por 8 volta pro 6, tá? Essa é a forma irredutível. E isso aqui é uma fração própria, tá? Agora, se primeiro eu apliquei uma divisão por 10, depois eu apliquei ainda uma divisão por oito, por quanto eu tô
dividindo no total? Por 80, tá? Porque eu dividi por 10 e por 8, então 10 x 8 dá 80, eu dividi por 80. E sim, eu poderia ter começado a dividir logo pelo 80, tá? Então poderia ter falado assim, ó, e eu poderia ter percebido que o 480 é divisível por 80, né? Porque você pode colocar 80, 160, 240, 320, 400, 480, tá? Então, 80 di por 80 1 480 di por 80, quantos pacotes de 80 cabem aqui, cara? Em 48 cabem seis pacotes de 8. Então, em 480 cabem seis pacotes de 80, tá? Então,
dá seis do mesmo jeito. 480 divido por 80 dá 6, tá? Seis números 80, 80, 160, 240, 320, 400, 480, tá? Essa é a fração irredutível, tá? Vamos continuar. Deixa isso aqui irredutível, cara. Você vai ter que investigar. Você pode pensar assim: "Ah, acho que não dá não, né? Você tem que investigar se eles são divisíveis os dois pelo mesmo número. Dá para dividir os dois por dois? Não dá. 12 dá por 2, dá. 135 não dá, porque 135 é ímpar, então não dá para dividir por 2 e por 3. Dá para dividir por 3
dá 1 + 2, 3.5 dá para dividir por 3 dá 1 + 3 4 + 5, 9. 9 é divisível por 3. Ou seja, eu posso simplificar isso aqui dividindo em cima e embaixo por três. Talvez tenha outro número que funcione. Eu acho que não, mas talvez tenha, tá? Mas eu acho que o 12 é divisível pelo 3 e o 135 é por 3. Eu tenho certeza disso. Eu já vou logo dividir por três, tá? Então, divide por trê em cima vira 4. Divide por três embaixo. Como é que você vai fazer? Pensa assim, ó.
Em vez de dividir 135 por 3, divide 120 e depois divide o 15, né? 120 por 3 dá 40 e 15 dá 5, então dá 45, tá? Então 135/ 3 dá 45, faz 3 x 45 vai voltar para 135. E agora dá para dividir em cima e embaixo por dois? Não dá, porque aqui é ímpar e por três também não dá. Esse até dá para dividir por três, mas esse não dá. Dá para dividir em cima e embaixo por quatro? Aí em cima dá. Embaixo não dá. 45 não é divisível por quatro. Teria que teria
que ser parpa começo de conversa, né? Então não é, dá para dividir em cima e embaixo. Pera aí. Não tem nem mais o que perguntar. Porque tu já tentou dividir por quatro? Não deu. O não dá. Você vai dividir por cinco? Claro que não. O quatro já é ali e o topo. Se você não conseguiu dividir em cima e embaixo pelo quatro, você não precisa passar do quatro, tá? Nada vai funcionar. Então essa é a forma irredutível dessa fração, que é também uma fração própria, tá? Menor em cima e maior embaixo, OK? Se ela é
própria aqui, ela vai continuar sendo aqui, tá bom? Só para constar. 78/ 399. Você pode falar: "Caramba, isso aí não deve dar para dividir não". Vamos ver. Dá para dividir em cima e embaixo por dois? Em cima dá, porque em cima é par, embaixo não dá, porque embaixo é ímpar, tá? E por 3, 7 + 8, 15. Em cima dá por 3, tá? Embaixo 9 + 9, 18 + 3, 21. Opa! Embaixo também dá para dividir por três. Então assim, eu não vou nem ficar tentando. Eu sei que não vai dar para dividir nenhum dos
dois, nem por cinco, nem por 10, né? Eu sei que não vai dar para dividir. Eh, então assim, eu acho que o dividir por três para mim já tá bom aqui. Aí depois que eu dividir por três, eu vou ver o que que tem para eu fazer, tá? Então vamos lá. 78 por 3. Cara, pensa em fazer o 60 mais o 18 por 3. Então, quanto que é 60 por 3? É 20. E o 18 é 6. Então, 26. Dividir em cima por 3, tá? E também embaixo vou dividir. Em cima por 3 dá 26,
tá? Confere. 3 x 20 60. 3 x 6 18. 60 + 18= 78. E agora embaixo, como é que eu vou dividir por três? Pensa em dividir o 300 e depois o 99. Faz isso com os dois, tá? Vou dividir o 300 e vou dividir o 99 por 3, tá? 300 por 3 dá 100. 99 dá 33. Então 133. 133. Pronto. Resposta 26/ 133. Eu te pergunto, mas essa já é a forma irredutível dessa fração? Vamos ver. Dá para dividir em cima e embaixo por dois? Não, porque aqui é ímpar. E por três também não,
porque 2 + 6 dá 8. E por qu não dá. 26 não é divisível por 4. Então assim, se um deles não dá, não precisa nem testar o restante, né? Por cinco não dá. E por 6 também não dá, porque 26 não é divisível por 6, tá? É 6, 12, 18, 24, 30, né? Por 7 também não, né? Eu tô testando um deles só porque tem que ser os dois divisíveis pelo mesmo número. Se um não for, eu já descarto. Dá para dividir por oito? Não dá, né? Dá para dividir eles dois pelo nove? Também
não dá, né? Não dá nove, não dá um número divisível por 9 a soma dos algarismos. Dá para dividir os dois por 10? Não dá. Aí você pode falar: "Então, acabou". Não, você ainda tem que testar o seguinte: será que dá para dividir, por exemplo, por 13? Aí você vai ver que, calma aí, o 26 dá para dividir pelo 13. Se eu dividir 26 por 13, dá 2. Embaixo? Embaixo dá? Não. Embaixo não dá, porque 13 x 10 já dá 130. Então o 130 é divisível pelo 13. Mas depois que você bota mais 13, você
vai direto pro 143. Então o 133 não é divisível pelo 13, tá? Só que galera, o 26 agora ele só vai ser divisível de novo por ele próprio. 26, né? Se ele não foi divisível por 13, agora você só que por 13 iria ficar meio a meio. Agora você só pode dividir 26 por 26. Embaixo dá para dividir, por acaso embaixo por 26 também? Vamos ver. 133 é divisível por 26. Vamos ver, né? A tabuada do 26. 26 52. Vou dobrar aqui logo, tá bom? Ao invés de eu botar mais 26, eu já vou dobrar
esse aqui logo para 104. Agora o 104 bota mais 26 nele, né? Vai ficar 130. Aí agora, ou seja, essa é a forma irredutível da fração. Não dá para ela ficar menor do que 26/ 33, tá? Então essa é a forma irredutiva também é uma fração própria. Aqui 17/ por 171, né, bicho? Não dá para dividir eles por dois, não dá para dividir por o 17 é primo, já começa por aí. O 17 só pode ser dividido ou por um ou por ele próprio. Então você já não vai nem ficar testando 3, 4, 5. Cara,
o 17 eu só posso dividir por 17 que vai dar um. Mas e aqui embaixo eu consigo dividir isso aqui por 17? Não consigo, bicho. Tá? Não consigo. Se fosse aqui embaixo 170, aí tava lindo. 170 di por 17 dá 10, né? Porque 10 x 17 vira isso aqui. Mas não dá porque tem um um aqui. Ou seja, essa forma aqui já é a forma irredutível, ok? 700 por 8, cara, com certeza vai dar para simplificar, porque eu posso dividir os dois por dois, eles são ímpares, tá? E por qu, será que dá para eu
cortar caminho e já dividir logo pelo quatro? Talvez fosse melhor assim, né? Já dividir pelo quatro dá, porque os dois últimos aqui são 0 zer e embaixo o oito é divisível pelo quatro, né? Todo mundo sabe disso. Então, já vou fazer isso. Ai, será que dá para dividir por oito, né? Aí eu não sei, cara. Eu poderia até testar, mas eu acho que eu vou dividir por quatro mesmo, tá bom? Então vou dividir por 4 em cima e embaixo, tá? Vou fazer aqui embaixo. 8 di por 4 dá 2. Pronto. E 700 di por 4
eu vou dividir por 2 e por 2 que dá no mesmo, tá bom? 700 por 2 350. 350 por 2 175, tá? Porque 340 é 170. Então botou mais 10, fica 5 para cada um, tá? 175/ 2. Isso está irredutível? está porque eu tenho que dividir em cima e embaixo pelo mesmo valor, mas o máximo que eu posso aplicar é do e 2 por 2 dá, dá, mas 175 por 2 não dá. Então isso aqui é a forma irredutível e essa aqui é uma fração imprópria, entendeu? Essa fração é imprópria porque ela tem a parte
de cima maior, tá? Então ela é a primeira imprópria que aparece aqui porque todas elas tm a parte de cima pequena. Ela tem a parte de cima, essa aqui tem a parte de cima maior, tá? Então ela tá na forma irredutível aqui e ela é uma fração imprópria, tá? 31/ 15, outra fração imprópria, porque tá maior em cima do que embaixo, então é imprópria, né? Agora, para ser aparente teria que dar para dividir certinho. Se fosse 30/ 15, ela seria imprópria e aparente, porque 30/ 15 dá 2, tá? Mas não é o caso não, galera.
Dá para eu fazer a mesma coisa em cima e embaixo? Não dá. Eles não são divisíveis por dois. Eles não são divisíveis por três, né? Ele até é, mas o 31 não é, né? O 31 é primo, inclusive o 31 só dá para dividir por um e por ele mesmo. Então assim, não tem nada para fazer aqui. Não dá para dividir por cinco só embaixo, mas em cima não. Não dá para dividir por sete? Claro que não. Nenhum dos dois dá. Nem por oito, nem nem porve. Não dá para dividir isso aqui por por 15
em cima e embaixo. Aqui dá por 15, mas aqui não dá. Então essa forma aqui já é a forma irredutível, tá? 32 por 4. Isso aqui é uma fração novamente imprópria, porque tá maior em cima, embaixo. Só que além dessa fração aqui ser uma fração imprópria, ela é também uma fração aparente. Por o de cima dá para tu dividir pelo de baixo perfeitamente. Então você pode fazer o quê? 32/ 4. Quanto que é o 32 dividido pelo 4? Assim diretamente 8. Entendeu? Então se tu dividir aqui o 4 pelo próprio 4, vai dar 1 e
o 32 pelo 4, vai dar 8. Só que 8/bre 1 não é nenhuma fração. 8/ 1 é só o próprio 8 mesmo, tá? Então assim, isso aqui é uma fração aparente, porque no fundo 32 por 4 você pode fazer a divisão e dizer assim 8. Então nem precisa falar de fração, tá? 81 por 27 fração imprópria, porque em cima tá maior do que em baixo. Agora e para simplificar isso aqui, tá? Para simplificar isso aqui, ó, vou dividir em cima e embaixo por dois, não dá. E por três dá? 8 + 1 dá 9. Dá,
dá para dividir por 3. Embaixo 2 + 7 dá 9, também é divisível por 3. Então vou dividir em cima por 3, tá? Vou dividir embaixo por 3, vai dar 9. em cima por três vai dar 27, tá? 81 por 3 dá 27. Agora dá, tá, tá na forma irredutível, não. Eu posso dividir em cima e embaixo por por três. Divide embaixo por três, dá três. Divide em cima por três, dá 9. Tá? Agora eu posso pegar o 9/3 que eu tenho aqui e dividir em cima e embaixo por três, tá? Então embaixo eu dividi
por três deu 1, em cima por três deu 3. 3/ 1 que não é nenhuma fração, né? Isso aqui é só três. Ou seja, já começa que isso aqui era uma fração aparente. Por quê? Porque eu posso pegar aqui e literalmente dividir 81 por 27. Essa divisão vai dar certo. Então isso aqui não é nem fração. Isso aqui é fração aparente. Na verdade é fração, mas é fração aparente, tá? Ou seja, bastava dividir o 81 por 27. Agora eu também fiquei dividindo de três em três, galera. Eu poderia ter já dividido por 9, né? Porque
8 + 1 dá 9, é divisível por 9. E 2 + 7 dá 9, divisível por 9. Então 81 por 9 dá 9. E 27 por 9 dá 3. Agora 9 por 3 dá 3. Tá? Cheguei mais rápido que na minha resposta, mas isso aqui é uma fração aparente, tá? Eh, 94/ 47, tá? Mais uma fração aparente, porque dá para dividir o 94 pelo 47, tá? Não precisa vir aqui neles dois e ficar tentando aplicar divisões, tá? Você pode dividir 94 pelo próprio 47. Então, é a mesma coisa que você dividir em cima e embaixo
por 47. 47 por 47 1 e 94 por 47. Tá? Então, ou seja, o 94 é o dobro do 47, só isso, tá? fração aparente. 273/ 27, tá? Será que dá para dividir os dois por 3? 2 + 7 9 + 3 12. Opa, 12 divisível por 3, bom sinal. E 2 + 7 dá 9, que também é divisível por 3. Bom sinal, tá? Eh, Pedro, daria para dividir por 9 de cara? O 27 até dá, mas esse aqui não dá, porque 2 + 7, 9 + 3, 12. 12 não é divisível por 9, tá?
Então eu vou dividir por três mesmo, tá? Então dividi aqui embaixo por três, primeira coisa, tá? Isso aqui é uma fração imprópria porque tá maior em cima. Divide aqui o 27 pelo 3, tá? Vai dar 9. Divide o 273 pelo 3. Cara, imagina dividir o 270 e o 3 porque é 273. Então 270 você tá, lembra que você tá dividindo por 3, tá bom? Por favor, em cima e embaixo por 3. 270/ por 3, cara, 27 por 3 dá 9. Então 270 por 3 dá 90. E 3 por 3 dá 1. Então 91. Percebeu? Dividir
por 3 em cima e embaixo. Deu isso aqui. 91/ 9. Dá para fazer alguma coisa aqui ainda, né? Não dá para dividir por três, né? Porque o 9 até dá, mas o 91 não dá, porque 9 + 1 dá 10, né? Não dá para dividir isso aqui por cinco. Não dá para dividir isso aqui por seis, né? Não, porque teria que ser par também, né? Não dá para dividir isso aqui por sete. Dá para dividir por? Não dá. O 9 por 9 dá, mas o 91 não dá. Ou seja, essa já é a forma irredutível
dessa fração, tá? Não tem mais o que fazer aqui. Isso aqui é uma fração imprópria, porém tá na forma irredutível já. Não tem mais o que fazer aqui, tá? 36 por 216, tá? Então, dá para fazer o quê? Dá para dividir por dois em cima e embaixo? Dá. Vai ficar 18 sobre 108. Dá para dividir de novo por 2? Dá. Vai ficar 9 sobre 54. Dá para dividir de novo por 2? Não dá, porque aqui tem um 9, tá? Dá para dividir por 3? É, 9 por 3 dá e 54 por 3 dá, porque 5
+ 4 dá 9. Então, 9 por 3 vira 3. 54* 3, tá bom? Eh, 30 por 3 já dá 10. Então, vou pensar aqui em 30 + 24, tá bom? 30 por 3 dá 10 e 24 dá 8, então dá 18. 3 sobre 18 dá para dividir por 3? Dá, vai ficar 1 sobre 6. Essa é a resposta. 1/6, tá? Mas, pô, eu não não vou fazer tão devagar assim. Eu vou começar já talvez dividindo por quatro, porque eu tô vendo que 36 é divisível por 4 e os dois últimos algarismos aqui também são divisíveis
por 4. Então aqui é tudo divisível por 4. 36 por 4 dá 9, tá? 216 por 4. Para dividir por 4 eu vou dividir por 2 por 2. Então por 2, 108 por 2 54. Já avancei muito mais rápido. Agora eu vou dividir em cima e embaixo por 9, porque eu vi que em cima e embaixo é divisível por 9. 9 é divisível por 9 e 54, ó, 5 + 4, 9. Dá para dividir por 9. Então 9 por 9 por 9, tabuada 6. Então 1/6, tá? Você pode observar que o 36 ele é 1/6,
tá? Então aqui, ó, aqui no 216 cabem seis vezes o número 36, tá bom? Então por isso que 36/ 216 é uma fração própria, onde é pequeno em cima. E ela vale 1/6 na sua forma irredutível. Beleza? Então esse foi o nosso treinamento aí absurdamente importante de simplificação de frações. Esse isso aqui é uma coisa de ouro para você ter na sua mente, na sua inteligência e é apenas o começo, tá bom? Então até a próxima. Parabéns por assistir mais uma aula e vamos para cima. Seja muito bem-vindo a mais uma aula da plataforma SAD
no nosso curso de matemática, tá? Agora matemática básica um, OK? Então, a gente tá começando aqui o nosso trajeto pela matemática básica, porém não se engane, tá? Não pense que nós estamos fazendo aqui coisas de iniciantes. É óbvio que sobre certo ponto, sim, mas o que nós estamos fazendo aqui, se você tá acompanhando as aulas, você tá percebendo que mesmo que você já soubesse a matéria, o nível de velocidade, de compreensão e de profundidade que você tá ganhando é um nível novo, é um nível superior. Pouquíssimas pessoas atingem esse nível. Até mesmo as pessoas que
passam em medicina muitas vezes não tem esse nível de compreensão e de velocidade da matemática e isso faz total diferença para você passar com muito mais força, tá, em qualquer curso que você queira. Então é isso que a gente tá fazendo. A gente tá focado aqui num desenvolvimento bem agressivo, um desenvolvimento mais bem fundamentado, tá bom? Bem sólido. E agora a gente vai aprender a somar e a subtrair frações. Então a gente vai usar para isso os nossos conhecimentos prévios que a gente obteve até agora, tá? Eu quero que você pense na situação em que
eu te digo assim, ó, 1/3 + 1/3, eu tô propondo uma soma de frações, tá? O que significa 1/3? Significa uma parte de um universo de três. E o que significa 1/3 aqui? A mesma coisa. Então, eu quero uma parte de um universo de três partes, tá? Agora, quanto que vale realmente 1/3? Você pode sempre dizer, vou abrir um espacinho aqui em cima só para não confundir. E se eu tiver falando assim de 1/3 em absoluto, né? Quanto vale isso aqui? essa fração 1/3, cara, 1 di 3 dá isso aqui 0,33, porém, né? E continua
assim, 0,33. Uma fração, ela geralmente serve para você não, você não tá falando dela por ela mesma, você tá usando ela para falar de outra coisa. Então, por exemplo, isso aqui é uma fração, você concorda? 1/ 2 é uma fração, né? 1/ 2 é o quê? Metade. Inclusive é a mesma fração de 2/ 4. Quanto vale 1/ 2? Vale 0,5, né? meio e 2 sobre 4 vale a mesma coisa, 0,5 são frações equivalentes que valem a mesma coisa. Porém, com frequência a gente usa o quê? Esse meio aqui, né? Esse 1/2 ou essa metade para
falar de outra coisa. Então a gente fala assim, 1/2 R$ 40, quanto que dá isso aqui? Dá R$ 20, entendeu? Então você usa a fração, então 1/2 disso aqui você usa a fração para expressar uma parte de outra coisa, tá? Então, como 1/2 significa isso aqui, ó, 1/2 significa isso, ó, né? É uma expressão para isso que também pode ser expresso como 2/4. A diferença é que no 1/i eu tô falando disso aqui, ó, de duas partes, eu quero uma. E quando eu falo no 2/4, eu tô dizendo a mesma coisa. Porém, eu tô dizendo
assim, ó. Se fossem quatro partes, eu ia querer duas. Mas repara que nos dois casos, você tá falando da metade e assim vai, né? Se você colocar, ah, isso aqui também, Pedro, se para para pensar, é igual a 4/8, né? Dobrou aqui, dobrou aqui. 4/8. Sim. Aí para você entender, você teria que botar oito partes aqui, né? E dizer que dessas oito partes, 1 2 3 4 5 6 7 8. Dessas oito você quer quatro, mas você ainda estaria expressando a mesma coisa, né? Ou seja, e quando você sabe disso, você entende isso, aí fica
faz sentido, né? Por que que dizer 1/2 de 30 é igual a 15? Porque 1/2 significa metade de qualquer coisa. Então 1/2 é justamente metade de 15. Você pode multiplicar, você vai ficar com 30 sobre esse dois aqui. Eu vou te mostrar isso com calma, tá? Daqui a pouco, na próxima aula, você vai aprender melhor sobre multiplicações. Mas eu tô fazendo essa introdução aqui para você, você vai entender já para que que isso aqui vai ser útil, tá? Pode confiar em mim. Então agora você tem essa situação, 1/3 + 1/3. Bem, eh, não, já ficou
claro para você que esse 1/3 não necessariamente quer dizer, né, que são três coisas. Então assim, 1/3 do meu dinheiro, se eu falar para você assim: "Vou te dar 1/3 do meu dinheiro, eu não tô dizendo que eu tenho só R$ 3 e eu vou te dar R$ 1.". Eu não tô dizendo isso, né? Quando eu falo assim, vou te dar 1/3 do quê? Do dinheiro. Quanto que isso vale? Depende de quanto dinheiro eu tenho. Se eu falar para você assim, ó, eu tenho no total R$ 90 de dinheiro. Nesse caso 1/3, nesse caso vale
30, né? 1/3 de 90 é isso. É você pegar o 90, dividir por três partes e você só quer uma. E no caso do 90, cada parte tem 30. Se fosse 2/3 do 90 já seria 60. Agora, se fosse 1/3 de 90 seria 30. E se fosse 1/3, na verdade de 1/3 de 150, né? 1/3 sempre vai ser uma parte de três, mas nesse caso são partes de quê? De 50, né? E você de todas essas partes de 50 só que é uma, tá? Beleza? Ou seja, né? Sabendo disso, quando eu tenho 1/3 + 1/3,
tá? Não interessa de quem eu tô falando. Ele não disse ainda 1/3 de quem, não falou nada, tá? Só falou assim 1/3 mais 1/3. Mas eu ainda assim consigo relacionar isso porque uma parte no universo de três mais uma parte no mesmo universo de três, né? Eu tô falando as duas em universo de três, supondo que existem três coisas, eu quero uma. O como é que eu faço essa soma? Eu simplesmente repito o denominador. Então, a resposta é o mesmo três aqui embaixo e aqui em cima eu efetuo de fato a soma. Então, 1 +
1, quanto que dá 1 + 1? 2. Então, a resposta é 2/3. 1/3 + 1/3 é 2/3, tá? Ou seja, no primeiro caso, eu falei assim: "Cara, pensa que existem três partes de qualquer coisa. Eu quero uma, tá? Agora eu vou somar com outra fração." E essa outra fração também tá escrita na mesma linguagem, tá? Tá escrita com o mesmo denominador. Então, é fácil pensar nelas juntas. Ó, pensa em outro universo de três partes, mas também tem três partes, que nem o primeiro. E eu quero uma parte desse universo, tá? Agora eu quero que você
some isso que eu tenho, uma parte de um universo de três e outra parte de outro universo de três. Ou seja, juntando, eu vou ter um universo de três. Não pense que eu vou ter aqui um universo de seis, né? Não pense isso, porque eh a gente tá falando do No final das contas, a gente tá falando ali de da junção do mesmo sistema numérico. Então assim, a cada três partes eu quero uma. Essa é a informação. A cada três partes eu quero uma. E aqui a informação é: "A cada três partes eu quero uma".
Tá? Então, ou seja, quantas partes de fato existem? Existem três partes, porque a gente tá sempre aqui falando de três partes, tá? O que muda é que aqui eu disse uma, aqui eu disse outra, tá? A soma disso você repete o denominador porque ele já está igual. Então quando o denominador tá igual, é a mesma coisa que eu falar para você assim, ó. Eu tenho aqui metade. Eu quero que você me dê a sua metade. Quanto eu vou ficar? Você não vai concordar que eu vou ficar com 2/ 2, né? 2/ 2 é 1. Você
não vai estranhar. Você não vai falar: "Tinha que ficar quatro aqui". Claro que não. Claro que não, tá? Se aqui ficar quatro, não vai mais fazer sentido, né? Porque eu peguei aqui, ó. Vamos pensar aqui que isso aqui representa é, vamos pensar aqui concretamente, né? Eu tenho aqui, é, vamos, dá pra gente pensar aqui pelo exemplo que eu mesmo coloquei. Você tem ali embaixo a representação da fração em pizza. Então, o que que essa primeira fração 1/ç representa? Ela representa exatamente isso, tá? Ela representa, pensa, pensando em três coisas totais, você quer uma, então tá
desenhado aqui. E a outra fração é a mesma, né? Então, eu vou expressar ela da mesma forma, mas eu vou colocar aqui a outra parte, né, para não ficar no mesmo lugar, embora não precisar. Se, se eu quisesse eu poderia fazer aqui, não ia mudar em nada. Mas é só para você ter uma noção, quando eu junto isso aqui, não é não é claro que eu vou continuar considerando a que só existem aquelas três partes, porque, né, porque na verdade, galera, tanto faz o número de partes que existem. Esse é o plot aqui. Tanto faz.
A, eu continuo no mesmo universo. Então, por exemplo, se eu falar para você assim, ó, eu tenho aqui 3/4 de pizza e eu quero juntar com o teu 1/4 de pizza, né? Eu, a gente tá pensando o quê? Numa pizza inteira que a gente não sabe também qual o tamanho dela, né? A gente não sabe essas, não sabe qual o peso dela, nada disso. A gente sabe o seguinte, ó. É uma pizza inteira. Se a pizza é grande, se ela é média, se ela é pequena, né? Não interessa. Eu tô dizendo assim, se você tem
100 pizzas ou não, não muda nada. Eu tô dizendo assim, a cada pizza inteira, eu tô falando de 3/4 dela, né? Sendo uma pizza ou duas ou ou 100. Eu quero sempre falar 3/4. Isso agora eu vou fingir que a gente tá função só de uma pizza, tá? Então, 3/4 de pizza, né? A princípio, a gente tem uma pizza dividida em quatro partes e a gente tá se referindo ao quê? A três partes dessas quatro. Até aqui tudo certo. Aí vem outra pessoa ali e fala 1/4 de pizza, né? Ela diz isso. Eu tô representando
aqui do lado. Ela diz 1/4 de pizza, né? Ela tá falando disso aqui. Tá falando de uma pizza de quatro pedaços, mas ela só quer um, né? Mas aí que tá. Dá uma pausa aqui e pensa no seguinte, né? Claro, quando eu vou somar isso aqui, eu vou repetir o denominador porque ele tá igual. Então vai ficar aqui quatro. E aqui em cima que eu vou somar 3 + 1, tenho quatro partes. Ou seja, no fundo você tava falando de quê? 4/ 4. Simplificando por quatro em cima e embaixo, né? Vamos dividir por quatro aqui
vai dar quanto? 1. Divide por quatro aqui também vai dar 1. 1 sobre 1. Ou seja, percebeu? Se eu tenho quatro pedaços a cada quatro pedaços, isso é a mesma coisa que eu dizer que eu tenho dois pedaços a cada dois pedaços. É a mesma coisa que eu dizer que eu tenho um pedaço a cada um pedaço. Esse é o truque para você ter compreensão perfeita, muito rápida e muito estruturada de frações. É você entender isso aqui. Isso aqui é matéria do sexto, sétimo ano, né? Mas é importante a gente estudar. Maioria das pessoas esmagadora
tem deficiência nisso, inclusive alunos de autodesempenho, tá? Então, ou seja, 4/4 é a mesma coisa que e 2/bre 2 é a mesma coisa do que 1 sobre 1. É a mesma coisa, tá? Por quê? Porque nos dois casos eu tô sempre me referindo ao total. Então assim, de cada quatro pedaços eu tenho, eu tô falando de quatro, tô falando da pizza inteira. De cada dois pedaços, tô falando de dois, tô falando da pizza inteira. De cada um pedaço tô falando de um, tô falando da pizza inteira, então tô falando da mesma coisa. Ou você acha
que se eu tenho aqui, né, a menos que você ache o seguinte, a menos que você pense que quando eu tenho duas pizzas, né, se você acha que eu passo a ter mais pizza, vamos supor, tem aqui uma pizza, né, quatro pedaços. Aí eu falo assim: "Ah, eu quero falar de 1/4 dela. 1/4." Mas você por acaso pensa que se eu se eu chegasse aqui nessa pizza e cortasse agora ela em oito pedaços, você pensa por acaso que eu teria mais pizza agora? Porque antes eu tinha 1/4to, aí agora, né? Eu tinha 1/4to, eu dobrei
o número de pedaços. Então, de oito pedaços agora eu tenho dois. É claro que eu continuo tendo a mesma quantidade de pizza, né? Se a gente quiser pensar na mesma pizza, a gente vai só dizer que os pedaços estão menores. Então, assim, de quatro pedaços grandes, eu tinha um. Agora ten oito pedaços menores, eu tenho dois. Mas dobrou o número de pedaços. Também dobrei o meu número de pedaços. Então eu tô falando da mesma quantidade de pizza, tá? Beleza? Se eu disser que eu tô dividindo ela em 16, ah, vou dividir a pizza em 16.
Só vai mudar que dessas 16 fatias eu vou ter quatro, mas eu sempre vou ter isso aqui, 1/4 da pizza. Isso aqui são frações equivalentes, mas eu sempre vou ter 1/4 da pizza, né? A diferença é que se você dividir em oito pedaços, o meu 1/4 vai ser 2/8. Mas nota que se você simplifica, você tem 1/4 ainda e dá para ver que você tem 1/4 aqui ainda, tá? Então, por isso que para você somar frações, você precisa ter essa compreensão de que a fração é uma forma de você simbolizar algo, tá? E quando você
tem os mesmos denominadores, a operação é muito simples. Você só precisa repetir esse denominador e somar a parte de cima, tá? Dando aqui o exemplo, então tenho aqui 1/3 + 1/3. Qual é a resposta? A resposta é 2/3. Então, supondo três pedaços, a gente tá falando de dois, tá? Essa é a somatória. Se eu tivesse aqui 1/3 + 2/3, a resposta seria o quê? Mantenho o denominador e 2 + 1 dá igual 3. Então 3/ 3. Ou seja, eu teria aqui, ó, 3. Aqui eu teria somado, deixa eu colocar aqui, ó, eu teria somado, ó,
1/3 com 2/3 e eu teria 3/3, né? Se a cada três partes eu quero uma e se a cada três partes eu quero duas, a somatória disso que a cada três partes eu quero três. Só que isso aqui é claro que é a mesma coisa do que 2/bre 2. É claro que é a mesma coisa do que 1 sobre 1. Divid por três em cima e embaixo é a mesma coisa do que um do que, ou seja, mas o que que é 1 dividido por 1? 1 dividido por 1 é um, ou seja, uma coisa
inteira. Mas não é isso mesmo? Três partes de três partes não é uma pizza inteira. Eu posso dizer assim, se eu quiser cortar essa pizza em 300 pedaços e falar assim, ó, é 300 de 300, isso continua sendo igual a um, não tá mudando nada aqui, tá? E aí eu consigo entender de quanta pizza eu tô falando, de verdade, tá? E aí é da mesma forma. Se você tivesse falado agora, olha o problema, olha, agora vou vou adicionar a complexidade aqui agora para você começar a pegar o ritmo, tá? Posso adicionar aqui a complexidade? Vou
fazer isso, tá? Olha o que eu vou fazer agora, né? Eu vou colocar, você tem 1/3 mais 2/6, quanto que dá? Olha que confusão, porque agora eu tô falando assim, ó. É, a pizza tem três fatias. Eu tô, a gente tá falando da mesma pizza sempre, né? Então eu falei assim, ó: "A pizza da qual a gente tá falando tem três fatias, mas dessas três fatias eu só quero uma". Falei isso para você aí você imagina isso aqui. Agora eu falo assim, agora soma isso com a seguinte. Tu vai falar qual? Falando dessa mesma pizza.
Porém, pensa nessa mesma pizza com seis fatias. Aí tu vai falar pensar nela com seis fatias, né? Isso já não é algo tão simples assim. 1 2 3 4 5 tá com seis fatias. Dessas seis fatias eu quero que você pegue só duas, tá? Colocar aqui assim, né? Representei aqui dois textos, né? Dois a cada seis. Aí eu falo assim: "Tá, quanto que dá a soma disso?" Eu te pergunto: "Cara, como é que você vai saber?" A gente tá falando da mesma pizza? Eu falei assim, falando da mesma pizza, se ela toda fosse dividida em
três pedaços, pensa em um desses pedaços. Pensa em você. Estamos falando da mesma pizza, ela não vai mudar, é a mesma pizza. Agora imagina que ela tá dividida em três. Quero só um pedaço. Mentaliza aí a mesma pizza. Agora eu vou cortar em seis e eu quero dois pedaços desses seis. Agora soma isso que eu quero. Aí tu vai falar assim: "Ué, mas eu vou dar a resposta em quê? Eu vou dar resposta considerando que a pizza tá dividida em seis ou em três?" E tu não entende como fazer isso, porque não dá para comunicar
esses mundos em que você pensa na pizza. Em uma hora ela tá com dividida em três fatias, tu quer uma que é 1/3ço. Em outra hora você quer que eu pense que ela tá dividida em seis fatias e das seis você quer duas. complicado. Como é que eu vou saber de quanto você tá falando no total? Para isso que se usa o mmc, para isso que você tem que saber colocar as frações com os mesmos denominadores. Por exemplo, você pode fazer isso de duas formas aqui nesse caso, né? 1/3 você pode manter, falar assim, ó,
vou deixar 1/3 mesmo. Mas tá vendo aqui o 2/6, você pode fazer uma operação nessa fração em cima e embaixo. Vou dividir em cima e embaixo por dois. Então aqui, ó, vou dividir por dois em cima e vou dividir por dois embaixo. Então aqui vai ficar um, concorda, né? Vou até apagarqui para não confundir. Então vai ficar mais o quê? Dividir por dois aqui em cima. Um. dividir por dois aqui embaixo 3 ela ué 2/6 para 1/3 continua sendo a mesma fração, porque eu apenas simplifiquei, né? A gente já fez vários exercícios sobre isso e
agora eu consigo ver claramente, ó, mantenho o denominador 2/3. Ah, você tava falando disso, tava falando que se a gente pensar que a pizza tá dividida em três fatias, você quer duas, tá? Mas eu poderia também ter feito o seguinte, mantido esses 2/6 e transformado 1/3. Então, como é que eu deixo eles com o mesmo denominador? Tá vendo esse três aqui? Eu quero que ele vire seis, então eu vou dobrar ele. Só que se eu vou dobrar aqui embaixo, eu vou dobrar em cima também. Então, ó, dobrei, virou seis, dobrou em cima, virou 2/6. Ou
seja, porque eu fiz de propósito para essas frações serem iguais, mas poderiam não ser iguais. É que eu quis que as duas fossem a mesma coisa, tá? Então aqui esse 1/3 eu vou escrever como 2/6 e esse 2/6 eu vou manter como 2/6. Repito aqui o denominador porque agora a gente estabilizou isso. A gente tá no mesmo universo. Nós estamos falando dessa pizza como se ela estivesse dividida em seis. E você disse que você quer duas partes, depois que você quer mais duas. Então você quer quatro partes de seis, tá? Eu então ou seja, mas
primeiro tu queria 2/3, agora tu quer 46. É a mesma coisa, porque eu tô somando aqui os mesmos números, tá? Essas frações aqui não vão mudar porque eu tô simplificando ou porque eu tô multiplicando elas, tá? Só que agora eu consegui fazer a soma. Só que é claro que você vai entender que isso aqui é a mesma coisa que isso, né? Então assim, no fundo 2/3 é a mesma coisa que 4/6, tá? Você eh pode estar olhando, né? Você pode estar falando assim, ó, o total dá 2/3. Então eu quero essa parte aqui e essa
parte aqui de três, eu quero duas. Ou você pode falar assim: "O total dá 4/6, né? Dobrou em cima, dobrou em baixo para representar a mesma coisa". Aí eu quero falar de 1 2 3 4ro partes. Olha como vai ser a mesma coisa, né? Você só não tá falando dessa parte aqui nos dois casos. A gente tá sofrendo a mesma coisa. E se você quisesse fingir que a pizza tá dividida, vamos dobrar aqui, ó. Dobra embaixo, dobra em cima, vai ficar 12 embaixo e oito em cima. Se quiser fingir que a pizza tá dividida em
oito pedaços, não tem problema algum. Vai dar certo da mesma forma. você vai táar falando da mesma quantidade, beleza? Então aqui, ó, né, fazer aqui bem rápido, você vai táar falando da mesma quantidade, tá? Então você vai tá querendo um, dois, é, depois eu faço, né? Divide em 12 aí, pinta oito partes que você vai ver que é a mesma coisa, tá? Em todos os casos, a gente tá falando de 2/3, ou melhor dizendo, né, para até completar a tua inteligência, eh, quanto que é 2/ 3? Você vai ver que dá 0,66. E quanto que
é 4/ 6? Obviamente é a mesma coisa, tá bom? 0,66. E o que significa 0,66? É uma forma de você dizer 66%, tá? Então 2/3 de algo é 66%, assim como 1/ 2 é a mesma coisa que 0,5, que quer dizer 50%, assim como 1 sobre 1 é a mesma coisa que 1 e 1 quer dizer o 100%, que é o total daquela coisa, tá? De que coisa agora? Aí depende do exemplo específico, tá? Mas agora vem o próximo problema que é o seguinte. Nesse caso aqui eu consegui igualar os denominadores, percebe? Eu fui apto
a igualar os denominadores apenas manipulando assim a fração de cabeça, né? Eu simplesmente virei aqui, deixa eu ajustar aqui a tela para ficar bonitinha. Eu simplesmente vim aqui e falei: "Essa daqui é 2/6, eu quero que isso aqui vire seis, eu vou dobrar para virar seis. Eu dobro em cima também. 2/6 + 2/6. Tá? Mas e se fosse um caso em que não é tão fácil assim, né? Simplesmente, tipo, esse caso aqui, eu falo para você assim, ó. Suponho que tem uma pizza. Porque naquele caso eu penso e falei assim, ó, finge que a pizza
tá dividida em três, depois em seis. Então eu dobrei de um pro outro, né? pensar nela em três, depois em seis, você consegue ter uma referência, né? Um a cada três. Aí se eu tiver falando de seis, eu tô falando de dois, né? Um a cada três e dois a cada seis, né? E três a cada nove. Beleza? E quando os universos, né, os universos, os denominadores, né, são mais incomunicáveis. Então assim, ó, imagina que a pizza tem três fatias, eu quero falar de uma, 1/3. Aí agora ele vem, mas imagina que ela tem quatro
fatias. Agora é a mesma pizza, mas eu quero falar de duas. Aí soma isso. Você vai falar: "Cara, como é que eu faço isso, né? Como é que eu que eu entendo quanto que eu tenho de verdade? Eu sei que aqui eu tenho metade dessa pizza, mas e aqui eu não tenho metade, aqui eu tenho 1/3. Mas como é que eu faço para entender quanto que é metade mais 1/3, né? Eu poderia, Pedro, entender que metade é o 0,5 e 1/3 é o 0,33 e dizer que eles dois juntos são o 0,83 com dízimo aqui?
Poderia, né? Mas isso não é a resposta em forma de fração, né? você precisa est totalmente apto a ver essa resposta em forma de fração, tá? Então, como que você faz isso? Ó, 1/3, você tá querendo falar de quê? De a cada três coisas você tá falando de uma, né? Supondo que essa pizza tá dividida em três, você tá falando de uma e 2/4. Supondo que agora a pizza tá dividida em quatro, você tá falando de duas partes. Caso ela esteja dividida em quatro, você tá falando dessas duas partes aqui. Mas e quando você soma
isso, quanto será que você vai ter realmente no total? você precisa visualizar no mesmo universo, igualar os denominadores. O problema é, como é que você iguala o três e o quatro, né? Não dá para eles ficarem iguais, mas você pode pegar essas frações e fazer coisas, né? Verificar os múltiplos delas até que você chegue a um denominador que as duas podem assumir. Então, por exemplo, você vai falar assim: "Ah, quero que essas frações tenham aqui, eu quero que elas tenham o mesmo denominador." Esse é o problema, né? Eu preciso que elas tenham o mesmo denominador,
porque eu só preciso repetir esse denominador, deixar ele ali uma vez e eu somo aqui 1 + 2, né? Só que, né, elas não tm o mesmo denominador. Um é três, outro é quatro. Você vai fazer elas terem qual denominador? Então, vai fazer elas terem o denominador oito. Não é bom, porque aqui eu consigo dobrar e fazer virar oito. Aí em cima eu faria virar quatro. Mas como é que eu vou fazer um negócio que é três virar oito? Não é bom para mim. Posso transformar em seis? É o três eu consigo dobrar e vira
seis. Eu dobro em cima, claro, 2/6. Mas e aqui? Como é que isso aqui vai virar seis? Ou seja, eu preciso de um múltiplo comum entre eles dois, né? E de preferência o mínimo. Então vou tirar o mmc entre eles, tá? Então, mmc entre 3 e 4. Só que, galera, quando você tem números assim, eh, pequenos, né, quando você tem assim apenas dois números e eles são pequenos, você pode simplesmente multiplicar eles. 3 x 4 dá 12, tá? Então, o isso é uma garantia de que o número 12 ele é feito, ele pode ser feito,
pode ser montado usando o 3 e o 4, tá? Então, 3 x 4 é 12. Ou seja, o 3 pode virar o 12, pode. Entendeu? Isso é uma G, quando eu multiplico um pelo outro, eu acho um número e com certeza eles dois podem virar esse número. Você concorda? Parece meio confuso, mas 3 x 4 dá 12. Isso significa que o 3 pode virar o 12. O 3 pode virar o 12, desde que ele seja multiplicado pelo 4. Ó que top, né? Se eu tenho que assim 4 x 3, quer dizer que o 3, o
4 pode virar um 12. Ele só precisa ser multiplicado por um 3. Ao contrário, por exemplo, de três vezes alguma coisa dando 11. Isso não existe. Só se for um número quebrado, óbvio, né? Mas eu quero só números inteiros. Então assim, 3 x 3 dá 9, 3 x 4 dá 12. Nenhum. Três vezes nada dá 11, né? Só se for vezes o número quebrado. Vezes 3 x 3 vul alguma coisa, tá? Então é claro, se você quiser fazer o método da decomposição simultânea, você também pode, né? Você pode pegar aqui, ó, vou tirar o mmc
entre 3 e 4. Passa aqui esse risco. É, vamos botar número primo, né? Então, assim, os menores números primos primeiro o dois. Por que que eu botei o dois? Porque dá para dividir o quatro por ele, tá? Então assim, com três não vai acontecer nada, mas o quatro vai ser dividido, vai virar um dois. Agora eu boto outro dois, mato esse cara aqui e repete o três. Agora eu boto um três e matei esse aqui também. 2 x 2 4 x 3 dá 12. Ou seja, o que que isso revela? Que essas duas frações elas
podem se transformar no 12, o denominador delas, né? E você vai falar assim: "Pronto, as duas vão se transformar no 12". Então tu já mete aqui que a resposta tem o denominador 12. Porque quando as duas virarem por 12, você só vai repetir o 12 mesmo. Agora, o problema é o seguinte: você não pode meter o 12 aqui e falar assim: "Agora 1 + 2, 3." Não pode fazer isso. Não pode mesmo, tá? Por quê? Porque para esses denominadores aqui se transformarem no 12, a fração precisou ser multiplicada por algo. Por exemplo, no caso dessa
primeira, o que que fez com que uma fração que era 1/3 virasse alguma coisa 12? Ela teve que ser quadruplicada. Então, em cima ela também vai ser quadruplicada, vai virar 4/ 12, tá? Então, na verdade, você não vai considerar aqui 1/3. Agora que você transformou o denominador em 12, você vai transformar aqui em cima em quatro. Por quê? Porque você quadruplicou o denominador para ele virar 12. Então aqui em cima você vai quadruplicar para continuar sendo a mesma fração, tá? Quadruplicar vai virar o quatro aqui. Beleza? Ou aí você pode fazer que nem seu professor
te ensinou, né? Ela faz o quê? Novo denominador é 12. 12/ 3 4. Porque eu sei que do 3 pro 12. 4 x 1. Bota aqui o 4 e faz aqui o mais. Tudo bem? 2/ 4, bicho. Mas o 4 virou 12. O que que aconteceu pro 4 virar 12? Ele foi triplicado. Então tu triplica aqui em cima também, vai dar 2 triplicado fica 6. Mas claro que você pode chegar aqui, né? Fala assim, ó. O novo denominador é 12. 12 dividido por 4 dá 3. Aí mostra que foi triplicado. 3 x 2 6. Então
aqui tava 4 x 1, 4 e 3 x 2 6. Ou seja, a resposta é 4 + 6, 10. E o denominador só continua o mesmo, óbvio, 10/ 12. Agora eu posso simplificar isso, né? Eu vou conseguir enxergar melhor se eu simplificar. Então, por exemplo, 10/ 12 é a minha resposta, né? Eu tenho 1/3 de uma pizza e metade, né, 2/4 de outra, eu somo, eu vou ter o quê? Eu vou ter como se fosse assim, se a pizza tivesse 12 pedaços, eu tô falando de 10, ou seja, eu tô falando da pizza quase inteira.
E claro que se eu dividir o 10 pelo 12, se eu pegar aqui e falar assim, vou dividir o 10 pelo 12, eu vou achar 0,83, né? 10 coisas para 12 pessoas, não chega a dar nenhuma coisa para elas, né? Elas vão ganhar zero, vão quase ganhar uma coisa inteira, tá? Então, porque naquela hora eu tinha achado aquele 83%, lembra? Mas agora que eu tenho essa resposta, eu vou simplificar para visualizar ela eh talvez num formato menor. Então, por exemplo, que operação eu posso fazer em cima e embaixo com os dois? Não dá para dividir
os dois por cinco, porque só o 10 vai por 5, o 12 não vai. Não dá para dividir. Só dá para dividir por dois, né? Então vou dividir por dois em cima e embaixo. Ó, por dois em cima virou cinco. Por dois embaixo virou 6. 5 sobre 6. Olha que top. O que que ele quer dizer? Se eu tenho 1/3 de uma pizza e 2/4 de outra, isso aqui equivale a eu ter o seguinte. Se você imaginar que é uma pizza, na verdade de seis pedaços, olha só que top. Se você imagina que essa pizza
tem seis pedaços, só um instante que eu quero fazer bonito, ficou meio desproporcional. Ó, agora ficou bem melhor. Desses seis pedaços, eu quero cinco. Olha só, de seis pedaços, tu quer cinco. Você vê que você já tá falando agora da pizza quase inteira, né? né? Você tá falando da pizza quase inteira. Então, antes você disse assim, ó, 1/3, imagina que a estamos falando sempre da mesma pizza, né? Precisamos estar no mesmo universo, né? Do mesmo tipo de pizza, né? Então, 1/3 dessa pizza, supondo que ela tá dividida em três, mas agora pensa que ela tá
dividida em quatro e pensa só em dois pedaços desse quatro, quanto que isso dá no total? Aí a resposta ainda é uma outra coisa. A resposta é não. Então tu imagina que ela tá dividida em seis, ó. Pô, primeiro eu imaginei que tava em três, né? Depois eu imaginei que ela tava dividida por quatro. Agora eu vou imaginar que tá por seis. E se tivesse por seis, seria cinco partes. Ou seja, estando por seis, eu tô falando então no total, somando aqui essas duas coisas disso mais isso mais isso mais isso mais isso. A pizza
quase inteira, quase inteira, né? Só sobra um pedacinho ali dela que eu não estou me referindo, entendeu? Agora, se você tivesse pegar esse 1/3 e tentar dobrar ele, vou dobrar ele para visualizar melhor, tu ia visualizar isso, 2/3, tá? 2/3, né? 1/3 aqui é a mesma coisa que 2/6. Então eu botei aqui 2/6, seja nesse universo aqui em que a pizza tem seis pedaços, aqui eu estava falando já de dois pedaços. Então com certeza aqui, olha, olha isso. Eu vou fechar agora o seu raciocínio. Se você perder, volta nessa aula, volta agora e assiste de
novo, tá? Primeiro eu falei assim: "Ina pizza tá dividida em três pedaços, quero falar de um, imagina que ela tá dividida em quatro, quero falar de dois. Soma agora isso aqui, tô falando de quantos?" Bem, imagina que tá dividido em seis, quero falar de cinco. Mas e se eu já pegasse essa primeira parte aqui? e lesse ela de outra forma. Esse 1/3 aqui, eu lesse assim, ó, 2/6, tá certo, galera? É a mesma coisa. Isso aqui também é 2/6, né? Eu tô imaginando que eu cortei em seis pedaços. Eu tô falando de dois do, então
eu não mudei nada, nada. Eu só li diferente. Bem, mas esses dois textos, olha, olha a resposta. A resposta é: se a pizza tiver seis pedaços, se você imaginar dividir em seis pedaços, tô falando de cinco. Aí você tá me dizendo que eu peguei esses dois textos, somei isso e obtive isso. Deixa eu simplificar para você, né? Olha o que tá sendo apontado para mim aqui. Tá sendo dito o seguinte, você pegou 2/6, somou com alguma coisa, vou até apagar aqui, e você chegou nisso, 5/6, como eu botei aqui aquilo que era 1/3 nessa linguagem
de de pensar em um universo de seis pedaços, dá um isso dá um certo artifício pra gente usar, que é o seguinte, num universo de seis pedaços, a gente tá falando de dois e num outro universo de seis pedaços, e o total disso a gente tá falando de cinco. Ou seja, quantos pedaços foram adicionados num universo de seis pedaços, você tem que imaginar o quê? Vamos pensar agora só nesse universo de seis pedaços. Se você pensar na pizza assim como seis pedaços, então você sempre falando de seis pedaços, você tinha dois, botou mais alguma coisa
aqui que não se sabe e ficou com cinco. Ou seja, essa coisa aqui é três. Essa coisa é 3/ 6. Mas como que tava escrito antes? Não tava escrito 3/ 6, tava escrito 2/ 4. Mas repara o que acontece, né? Repara que 2/ 4 é a metade, né? Metade disso aqui. 3/ 6 também é a metade, então é a mesma fração. Mas é que para você fazer o 2/4 virar o 3/ 6, olha o que você teria que fazer. Tá vendo que o quatro você teria que aumentar ele em 50%, a gente não faz isso
geralmente com a fração. Pode fazer, mas não não é muito usual. Então pega o quatro e bota a metade dele próprio. A metade do quatro é dois. Faz isso, ele vai virar o seis. Pega o dois e bota a metade dele próprio. Metade dele é 1. Então 2 + esse 1 vai virar o 3/ 6, que é o que tá aqui em cima, tá? Então a gente visualizaria que 2/ 6 + 3/ 6 é o quê? Repete o 6, que nem eu fiz aqui. Soma o 2 + 3, você vai ter o 5/ 6, tá
bom? Isso é soma de frações, tá? Na próxima aula, a gente vai fazer os treinamentos avançados, em que a gente realmente vai fazer aqui as somas com mmcs diferentes, adicionando complexidade e você vai ver que você vai se desenvolver de modo maravilhoso, tá bom? Parabéns por ter assistido mais uma aula da plataforma SAD e até a próxima. Então, bora continuar aqui o nosso estudo de matemática na plataforma SAD. E agora a gente prossegue com a matéria de frações, certo? Então, nessa aula aqui, você vai aprender, você vai dominar a habilidade, né, as habilidades de multiplicar
e dividir frações, certo? Então, o seguinte, até então a gente já aprendeu como que soma e como que subtrai duas frações, certo? Basicamente você só precisa igualar os denominadores. Então, para você executar qualquer operação de soma ou de subtração entre duas ou mais frações, podem ser três, 4, cinco frações, tanto faz. Você só pode fazer isso se elas estiverem com o mesmo denominador. E para chegar ao mesmo denominador, a gente utiliza, né, tem duas formas. uma forma mais intuitiva, que é você simplesmente olhar pras duas ou três frações que estão ali e tentar e deixar
os denominadores iguais. Como? Multiplicando ali as frações por números semelhantes. Então você tem que olhar para aquelas frações, ó. Uma delas tem denominador 3, a outra tem denominador 4. Bem, tanto o 3 e o 4 tem o 12 como múltiplo comum. Então a fração que tem denominador 3 vai virar 12 e a 4 também vai virar 12. Aí você faz a adaptação no numerador. Aqui tem três, virou 12. multiplicou por quatro, o numerador também tem que ser multiplicado por quatro. Aqui era 4, virou 12, quer dizer, ela foi triplicada. Então o numerador também vai ser
triplicado. Quando a gente fala de multiplicar ou dividir frações, a regra é diferente, tá? Isso cai bastante. Você tem que ter domínio sobre isso. Então vamos lá. Se eu tenho aqui uma fração que é a sobre b vezes outra fração que é c sobre D, como é que eu faço para multiplicar essa fração por essa? É muito fácil, né? Multiplicar frações é extremamente fácil. Você vai gostar disso, porque multiplicar frações, você só precisa multiplicar o numerador pelo outro numerador e o denominador pelo denominador, tá bom? É simplesmente fazer isso e você já está tranquilo. Você
multiplica um por aqui e o outro por aqui. Então, por exemplo, se eu tenho aqui, ó, 3/5 x, né, xes 1/ 2, eu faço 3 x 1, que dá 3, e 5 x 2, que dá 10. Pronto, a resposta é 3/ 10. Olha que coisa fácil, né? Se eu quiser pegar esse 3/ 10 e multiplicar por 5/7, não tem estresse, né? A resposta é 3 x 5= 15. Ou seja, numerador vezes numerador, né? E 10 x 7. Beleza? A resposta aqui é 15/ 70. Nesse caso aqui, eu tô percebendo que, né, aqui não tinha como
eu simplificar, né? Quando eu multipliquei 3/5 por deu 3/ 10. E eu não tinha aqui como simplificar isso, tá? Mas agora que eu inventei aqui de multiplicar por 5/7, a minha resposta deu 15/bre 70. E bem, algo me diz que dá para simplificar aqui. Por exemplo, eu consigo perceber que parece que tanto 15 quanto 70 são divisíveis pelo mesmo número que no caso ser, tá? Porque o o 15 eu sei que dá para dividir por cinco, né? Porque para dividir por cinco tem que terminar em cinco ou em zero. E o 15 termina em 5
e o 70 termina em zero. Então eu vou dividir os dois por 5, tá bom? 15/ 5 dá 3 e 70 por 5 quanto é que dá? Bem, se fosse 35 por 5 ia dar 7, então 70 por 5 deve dar 14, que é o dobro, certo? Entendeu? Eu pensei assim, ó, quando é 35 di 5, eu sei que dá 7 por causa da tabuada. Então, e se for o dobro, né? 70 é o dobro, né? 70 di 5, que é o que a gente tinha aqui, vai dar o dobro disso aqui. Então, ao invés
de dar 7, vai dar 14, tá? Ou seja, eu dividi os dois aqui por 5 e eu cheguei na forma irredutível, tá? É assim que se multiplica a fração. Vale lembrar que em algumas situações você vai ter isso aqui, ó. 3/ 8 xes, sei lá, por exemplo, vezes 12. E aí você pode pensar, o que que é isso aqui, né? É uma fração vezes um número normal. É, mas você tem que entender que o todo número normal ele pode ser escrito como se fosse uma fração. Por exemplo, 12, tá só um 12 lá. Você sempre
pode colocar 12/ 1, né? 12 dividido por 1 não muda nada. Então, 3 x 12 dá 36 e 8 x 1 dá 8, tá? Ou seja, nessa situação que você tinha 3/8 x 12, bastaria você multiplicar os numeradores e repetir aqui o denominador, mas você tem que ter consciência de que você tá fazendo uma multiplicação de frações, que é numerador vezes numerador e denominador vezes denominador. Mas quando não tem denominador, a gente diz que é um porque eu tenho lá 80, não tem denominador. 80/ 1. Pronto, agora 80/ 1 tem denominador. 80 di por 1,
mas não muda nada porque dá o próprio 80. Mas isso te ajuda a visualizar a explicação, tá bem? e a visualizar a conta lá na hora da prova. Agora vem a parte que para mais para costuma ser um pouco mais confusa para mais gente, mas não tem nada de confuso aqui, que é a divisão de frações, que eu já vou ensinar logo, tá? Não tem por fazer uma aula só de multiplicação de frações para depois fazer uma aula só de divisão, né? Dá para fazer na mesma aula e aí depois a gente avança, a gente
faz exercícios mais complexos dessas duas coisas. Como é que eu faço divisão de frações? Por exemplo, eu tenho 3/ 5. Eu quero pegar isso e dividir essa fração 3/ 5 por uma outra fração, que é, por exemplo, 2/ 7. Você tá entendendo? Eu tô, no caso, pegando essa fração e dividindo por essa, tá? Então, seja, uma divisão de frações, tá? Eu poderia expressar isso aqui também como 3/5, ó, sinal de divisão por 2/7, tá? É a mesma coisa aqui e aqui, tá? Eu já te disse isso, né? que 3/5 aqui numa fração, na verdade é
3 di 5, tá? Então aqui eu tenho 3/5, mas eu vou pegar ele e vou dividir por outra fração que é o 2/7. Qual é a regra para você conseguir fazer isso? Tá, cara, isso aqui é uma coisa que você tem que gravar e você vai ver que você vai gravar fácil, que é o seguinte: repete a primeira e multiplica pelo inverso da segunda, tá? Muita gente fica confusa porque a gente fala assim, ó, para dividir frações, você repete a primeira e multiplica pelo inverso da segunda. E aí a pessoa pensa, ué, pera aí, é
divisão ou é multiplicação? É divisão. É porque é assim que se faz a divisão. Para você fazer a divisão de frações, você acaba fazendo uma multiplicação. Mas é da seguinte forma, ó. Eu tenho aqui essa divisão para fazer. Como é que eu faço? Repete a primeira fração. Então, aqui, ó, repete a primeira. Não é o primeiro aqui, não. É a primeira fração. Repete a primeira. Repeti. E multiplica pelo inverso da segunda. Então, para eu multiplicar pelo inverso da segunda, ou seja, 3/5 di por 2/7, repete o 3/5, mas em vez de dividir pelo 2/7, como
é que você faz isso para você dividir pelo 2/7? Você multiplica pelo inverso dele. Ou seja, você multiplica pelo Não é pelo 2/7, é pelo 7 sobre 2, entendeu? Isso aqui é o inverso da segunda, ó. Aqui tá 2/ 7 e aqui tá 7/ 2. Quando você executar, quando você fizer essa multiplicação, você vai obter aqui a resposta. Então, três aí, aí a multiplicação você faz normal. A multiplicação você faz normal, tá bom? Então, numerador vezes numerador e denominador vezes denominador. Então, 3 x 7 dá 21 e 5 x 2 dá 10. Então, 21/ 10.
Percebe qual é a resposta de 3/5/ 27? você repete a primeira, mas multiplica. A invés de dividir, você multiplica pelo inverso da segunda. E aí você vai obter 21 sobre 10. Beleza? Essa aqui é a resposta nesse caso. Então é isso, tá? É bem simples. E agora a gente vai fazer aqui os nossos treinamentos, OK? Então vamos lá. Aqui a gente tem uma multiplicação, né? Multiplica a fração 2/3 pela fração 4/5. Qual a resposta? Multiplicação não tem mistério, né? é numerador vezes numerador e denominador vezes denominador. Então, quanto é 2 x 4? 8. Quanto é
3 x 5? 15. Pronto, essa é a resposta. Não dá para simplificar porque o 8 e o 15 não tem ali divisores em comum. Não dá para dividir eles por dois ao mesmo tempo, nem por três, nem por cinco, nem por nada, tá? Qual é a resposta aqui? X7, numerador vezes numerador, 1 x 3 dá 3. Denominador vezes denominador dá 14. Tá bom? 2 x 7 dá 14. Essa é a resposta e não dá para simplificar porque o 3 e o 14 não tem divisores em comum, tá? Quanto é 5/8 x 2/3, tá? Multiplica o
numerador por numerador e denominador por por denominador. 5 x 2 é 10 e 8 x 3 é 24, certo? Então 5 x 2= 10. 8 x 3= 24. Dá para simplificar essa fração? Dá, porque o 10 e o 24 t divisores em comum. por exemplo, o 2. Então vou dividir o 10 por 2. Quanto é que vai ficar? Vou dividir os dois por 2, né? Então 10 por 2 fica 5. E 24 por 2 fica 12. Ótimo. Essa é a menor forma possível dessa fração. 10/ 24 virou aqui simplificado, né? O 5/ 12. São frações
equivalentes, então valem a mesma coisa. Mas está na na forma irredutível, está porque agora o 5 e o 12 não tem mais divisores em comum, tá? Então, mais um exercício. Só que agora nós temos aqui três frações se multiplicando. Não importa a ordem em que eu faça, o que importa é que eu multiplique aqui esses três numeradores. Eu tenho que multiplicar eles e eu tenho que multiplicar esses três denominadores também. Não interessa a ordem. Se eu vou fazer aqui, aqui, aqui, ou se eu vou fazer aqui, aqui, depois aqui. Se aqui embaixo eu vou fazer
aqui, depois vou para cá. O que importa é que eh a ordem de dos fatores não altera o produto, tá? Então a ordem em que eu executo uma multiplicação não muda em nada o resultado, tá? Então vamos lá, vamos fazer aqui essas três multiplicações. 3 x 5 15 x 2 30. Embaixo agora, 4 x 6 24. 24 x 3 você faz 3 x 24, 3 x 20, 60. 3 x 4= 12. Então dá 72. Só que claramente essa não é a Então, só para deixar, só para deixar claro, né? Não faria diferença se eu fizesse,
assim, ó, 2 x 3, 6 x 5, 30, né? Aí 4 x 3, 12 x 6, 72. Não, a ordem não altera o resultado. E agora, qual é a forma irredutível dessa fração aqui? Eu tô vendo que tem um número par em cima e embaixo, então com certeza dá para dividir eles por dois, tá? Agora eu consigo perceber também que dá para dividir por três, né? Dá para dividir por três em cima e embaixo, né? E talvez seja até mais fácil para mim, né? Por que que eu sei que dá para dividir por três? Porque
a soma dos algarismos desse cara aqui em cima, 3 + 0 dá 3, é divisível por 3. E aqui embaixo, 7 + 2 dá 9, também é divisível por 3, tá? Agora eu também já percebi que dá para dividir por seis, porque para dividir por seis você tem que ser par e divisível por três ao mesmo tempo. E o 30 é par e divisível por 3. E o 72 é par e divisível por 3. Então eu já vou dividir logo por seis, tá bom? 30 dividido por em cima e embaixo, óbvio, né? Então vou dividir
em cima e embaixo por 6. 30/ 6 dá 5 e 72/ 6, né? Pode ser aí um pouco mais complicado, né, para para algumas pessoas de de raciocinar isso, mas o 72/ 6 ele dá 12, beleza? Então e você tem que ter essa mentalidade. Como é que vai fazer? Pô, Pedro, tô com problema para dividir aqui o 72 pelo 6. Como é que eu posso raciocinar isso, cara? Divide ele pelo 3 x 2, porque o 3 x 2 é o 6, tá? Então 72/ 2 dá 36. Aí 36/ por 3 dá 12, tá? Eu dividi
assim, ó. Eu posso dividir primeiro pelo três e depois pelo 2, tá? Que eu tô dividindo pelo seis. Então, só aqui um detalhe, né? Aqui caiu no mesmo resultado que essa primeira, não é simplificável, já está irredutível, tá? Esse exemplo aqui é muito bom porque ele tem aqui uma fração negativa, tá? Note que isso aqui é a mesma coisa do que eu ter -4/ 9, que é a mesma coisa do que ter isso aqui, que é a mesma coisa do que ter isso aqui, né? Não faz nenhuma diferença onde o sinal de negativo está, se
ele tá no numerador, no denominador ou no traço da fração. De qualquer forma, essa fração inteira, ela é um número negativo, tá? Então não faz diferença nenhuma. Agora, então eu tenho aqui um número negativo vezes o número positivo. Galera, essa é a primeira coisa. Ah, Pedro, multiplicação de fração, você faz numerador vezes numerador e denominador vezes denominador. Tá certo? Mas também eu tenho que fazer os sinais, né? É que geralmente é tudo positivo, então o sinal não muda nada. sinal não tem importância, mas nesse caso aqui tem, tá? Então, independente se isso aqui é uma
fração, finge que isso aqui é um número, tá? E isso aqui também é outro número, tá? Então eu tenho aqui um número negativo vezes o número positivo, que não tá com sinal, mas é positivo. É, galera, a resposta tem que dar negativa, tá? A resposta tem que dar negativa. Quando você tem uma multiplicação e tem número negativo ali, o negativo ele sempre inverte. Eu já mostrei isso nas outras aulas. Então, ter um negativo quer dizer o quê? vai ficar negativo. Se tiver dois, fica positivo. Se tiver três, fica negativo. Quatro, positivo. Vai sempre invertendo. Eu
já falei isso em outras aulas passadas e vou falar de novo nas próximas aulas. Então não tenha medo, não tenha problema com isso, tá? Então beleza. Vamos, vamos seguir. Agora eu já sei que a resposta vai dar negativa. Se eu tivesse aqui -9 x 7, eu eu vou fazer 9 x 7. Claro que eu vou fazer, mas antes eu tenho que saber o sinal. Então vai ser uma coisa negativa vezes uma coisa positiva. Vai dar negativo. Agora 9 x 7 é 63, né? Eu pensei 63, escrevi 67. É 63, tá? Então isso aqui é -
63. OK? Agora vamos, né, aplicar isso aqui. Então é claro que o resultado vai dar negativo, mas e a fração, os números, né? 4 x 3 12 9 x 5 45. E aí dá para simplificar isso aqui? Dá. Eu consigo dividir os dois por 3 porque o 12 é 1 + 2, 3 é divisível por 3. E o 45 é 4 + 5, dá 9. Também é divisível por 3. Lembra? Critério de divisibilidade. Já dei aula disso. Então vou dividir por três eles dois. OK? Quanto é 12/ 3? É 4. E 45/ 3 é 15,
tá? Então 3 x 15 45. E o sinal de negativo, óbvio. Então a fração é - 4/ 15. Dá para simplificar mais? Não dá. Essa já é a forma irredutível dessa fração, tá? Vamos treinar agora mais aqui algumas divisões, OK? Então 2/3 di por 4/5. Só para deixar claro, é a mesma coisa do que 2/3 div por 4/5, tá bom? Essa dividida por essa é a mesma coisa. A regra é divisão de frações. Repete a primeira e multiplica pelo inverso da segunda. Então vamos repetir a primeira. 2/3 e multiplicar pelo inverso da segunda. 4/5 vira
5/4, tá? E a resposta aqui é 2 x 5 10 e 3 x 4 12. Dá para simplificar? Dá. Você pode dividir ele os dois, né? Por dois. Então 10 por 2 dá 5 e 12* 2 dá 6. 5/ 6 já está na forma irredutível. Não tem mais o que fazer aqui, tá? 3/ 7/ 2 é a mesma coisa do que 3/ 7/ 1 2. Repete a primeira, então vou repetir a primeira e multiplica pelo inverso da segunda. É 1 sobre 2, então o inverso é 2 sobre 1, tá bom? 2 sobre 1, que é
a mesma coisa que apenas 2, né? Mas eu vou deixar aqui o sobre 1 para ficar bonitinho. 3 x 2 6. 7 x 1 é 7. Então 6/ 7. Ok? 5/8 di por 2/3. Repete a primeira, 5/8 e multiplica pelo inverso da segunda. Então, multiplica pelo inverso. 2/3, o inverso é 3/ 2. Então, 5 x 3 15. E 8 x 2 é 16. Não tem como simplificar isso aqui, tá bom? Não dá para dividir eles dois por e nem dá para dividir por três e não dá para dividir eles dois por quatro. Então, assim, não
tem o que fazer aqui. Não tem nada, nenhum divisor em comum entre eles. Fica 15/ 16 mesmo. OK? Então, espero que você tenha aí aprendido a noção primária, a noção inicial, eh, de como que você multiplica frações, que é numerador vezes numerador e denominador vezes denominador, e como que você divide frações, que é repete a primeira e multiplica pelo inverso da segunda, certo? Parabéns por ter assistido mais uma aula da plataforma SAD e até a próxima. Tchau, tchau. Pronto, agora a gente segue para uma sequência de exercícios de frações e de número misto, tá bom?
Para você realmente ficar fé em tudo. Você vai aprender, isso cai todo ano na prova, pode cair dentro que está mandando muito bem. Vamos lá. Eu tenho aqui, eu vou fazer, depois eu apago. Eu tenho aqui 3/ 4 + 1 2. O meu meu raciocínio sempre vai ser o quê? Eu quero igualar esses denominadores. E aí é óbvio, Pedro, eu posso transformar esse denominador aqui em dois? pode, mas é uma merda, né? Porque tu vai, para tu fazer ele virar dois, tu vai ter que sempre fazer a mesma operação em cima e embaixo da mesma
fração, né? Então vou ter que dividir aqui por dois, vai virar dois e em cima vai ficar 1,2. Aí 1,2 sobre 2. Pô, tá certo, mas não é bonito, né? Então é mais fácil eu transformar esse denominador aqui em quatro. Você concorda? Eu só quero que eles fiquem iguais, tá bom? Então, vou transformar esse denominador em quatro. Como que eu faço para transformar ele em quatro? Eu dobro. E se eu vou dobrar aqui embaixo, eu vou dobrar em cima também. Acabou. Vou pegar essa fração, vou dobrar em cima e embaixo. Ela vai continuar sendo a
mesma fração. 1/ 2 é metade, ó. Dobra embaixo, virou quatro. Dobra em cima, virou dois. Continua sendo metade. 2 sobre 4 metade. Agora você soma elas. Como é que você soma frações que estão com o mesmo denominador? Você repete o denominador e soma em cima. 5/4. Essa é a resposta. Entendeu? A resposta aqui é essa, 5/4, tá bom? 5 sobre 8 + 1 sobre 4. Eu acho melhor o quê? Para deixar os denominadores iguais, eu acho melhor dobrar essa daqui, né? Vou ter que dobrar essa fração toda. Então, ó, vou dobrar. Tá vendo? 1 sobre
4 vai virar 2/ 8, tá bom? Dobrando em cima e embaixo. Virou 2 sobre 8. Repete o denominador que é 8ito. Soma em cima, 7 sobre 8. Pronto. Você começa a perceber que, na verdade, se você ficar bitolado fazendo aquele MMC clássico do CA, da primeira série, você muitas vezes perde tempo. Você antes de MMC, é muito raro precisar de MMC para somar e subtrair fração em geral, você só precisa fazer uma multiplicação para deixar os denominadores iguais, tá? Lembrando que ele pediu para deixar sempre em fração irredutível. O que que é uma fração irredutível?
É uma fração que ela não pode mais ser simplificada. simplificar uma fração e você conseguir deixá-la eh dividir ela pelo mesmo valor em cima e embaixo para deixar ela mais compacta, para deixar ela menor. Tá bom? Então, deixa eu só deixar minha caneta aqui menorzinha. 7/ 8 aqui é a resposta. Beleza? 2/ 3 + 1 3. Ué, o denominador já está o mesmo, já tá três. Então é 3/ 3. É um inteiro. A forma irredutível é isso aqui, né? É um. Essa fração aqui é um. Ela nem é uma fração aqui e real, né? Ela
é aqui, no caso, uma fração aparente. Tá show? 4/5 + 5/6, né? Tem aqui 4/5 + 5 sobre 6. Como é que eu vou deixar esses denominadores iguais? Agora vem o primeiro desafio, tá? Eu sei, tem gente aí falando, eu multiplico cruzado e tal. Sim, pega esse jeito aqui, vai ser mais rápido por enquanto. Pega desse jeito, tá bom? Você, quando você visualizar dois números assim estranhos, eu quero que você sempre saiba uma coisa, se você multiplicar um pelo outro, tu vai obter alguém, tá? Ah, é 1/6, né? Não é 5/6, não, viajei. É 1/6.
Mas enfim, como é que você faz eles ficarem iguais? Se você multiplicar um pelo outro, você sempre vai obter um número que é é meio idiota falar isso, né? Mas se você multiplicar um pelo outro, cinco pelo seis, você vai obter 30. E esse número que você vai obter, que no caso é o 30, ele não, só multiplica um pelo outro mentalmente. 5 x 6. Aí guarda esse número na cabeça. 30. Esse vai ser o novo denominador. Tu quer que os dois denominadores virem 30. E por quê? Porque esse 30 ele é múltiplo dos dois
ao mesmo tempo. Com certeza. Por que que o 30 é múltiplo dos dois? Porque, pô, o 30 veio justamente do 5 x 6. 5 x 6 dá 30. Então, é claro que o 30 ele é um múltiplo tanto do 5 quanto do 6. Então, ou seja, o que que isso significa? Que você vai conseguir transformar, você vai conseguir transformar tanto 5 no 30 quanto o 6 em 30. Entendeu? Por exemplo, como que eu Vamos lá, eu eu tô querendo dizer não, como assim precisa ser o menor? Não, não, não. Exatamente. Ah, tá, tá entendido pergunto.
Então, o 30 calhou que o 30 é o mmc, né? O 30 é o menor múltiplo que eles compartilham. Não tem outro múltiplo aqui que seja menor ainda do que o 30 que os dois tenham. Mas e se eu escolhesse fazer pelo 60? O 60 também é um múltiplo comum deles. Vai dar certo igual. Vamos fazer dos dois jeitos, ó. Vamos lá. Vamos transformar os dois em 30. Como é que eu transformo essa primeira fração em denominador 30? Tá? Eu tive que multiplicar por seis, então vou multiplicar por seis. Em cima também virou 24. E
essa aqui, como é que eu faço para um 6 virar 30? Eu preciso multiplicar por 5. Ele vira 30. Mas então se eu multipliquei por 5 aqui, em cima também eu multiplico, vira 5. Denominador tá igual, fica 30. 24 + 25, 29/ 30. Essa é a resposta, tá irredutível. Não tem nenhum número que eu possa dividir em cima e embaixo que vai fazer isso aqui ficar menor ainda, entendeu? É, você pode multiplicar as frações por números diferentes. É dentro de uma mesma fração que você tem que manter a mesma a mesma a mesma multiplicação. Mas
essa aqui, no caso, eu multipliquei ela por seis. Essa aqui eu multipliquei por cinco. Normal. O que importa é você manter a fração sendo quem ela é. Quando eu multiplico essa aqui, eu tenho que multiplicar em cima e embaixo pelo mesmo valor. Ela continua sendo quem ela é. Tá bom? Ali, ó. E se a parte de baixo da Olha, essa pergunta foi muito boa, por incrível que pareça, tá? É uma pergunta interessante. Ele perguntou assim: "Mas e se as partes de baixo da fração não fossem números que que compartilham algum múltiplo? Quero ver quem sabe
essa. Isso não existe. É impossível isso. Como assim? Se for aqui, ó, qualquer tipo de fração, 2/ 17 vezes e 5 sobre 149, 17 x 149 vai dar um número que é múltiplo tanto de 17 quanto de 149? Essa, essas perguntas é boa, ela pega muita gente. Quando eu fizer 17 x 149, vai dar um numerozão aí. E aí, como é que eu faço pro 17 virar esse numerozão? Eu multiplico ele por 149. E como é que eu faço pro 149 virar esse numerozão? Eu multiplico ele por 17. Entendeu? Ali 17 x 49 dá 2533.
Tá? Então aqui eu, como é que eu faço para esse denominador aqui virar 2533? Eu multiplico ele por 149. Aqui em cima eu também multiplico por 149. E como é que eu faço para esse 149 virar 253? Eu multiplico por 17. Aqui em cima eu vou explicar por 17. Acabou. Os denominadores vão ser esses vão ser iguais. Mas é uma baita pergunta boa. Mas eu conseguiria fazer também. Você consegue fazer de cabeça? Consigo, pô. 17 x 149. Consigo fazer de cabeça. Eu faria 150 x 17, depois tiraria um dos 17. 150 x 17 faria 1700
mais metade, que é 850. Então já ficaria 2550 - 1 dá 2500 e ã 50 - 17500 e 30 e 3, acho que eu errei alguma coisa, né? 37, né? Isso. 253, sei lá, nem lembro mais agora qual era o resultado que tinha dado, né? Eh,3. É isso mesmo, né? É isso aí. Acertei. Eu nem lembrava mais, né? Show. Então, olha só, vamos agora, lembra desse primeiro caso aqui de cima que eu tinha 4/ 5, só para deixar claro, tá bom? Só quem entender, era 17 x 149, eu fiz 150 x 17, depois eu tirei
um 17. Aí 150 x 17, eu fiz 100 x 17 mais metade. Aí fica 1700 mais metade de si próprio que é 850, 2550 - 1 ali 253. Tá bom? Aí, olha só. Eh, e se eu tivesse escolhido fazer aqui, ó, lembra do lembra do 4/5 sobre 1/6? Eu tava com 4/5 sobre eh mais 1/6. Se eu tivesse escolhido transformar os denominadores em 60, tá? Para esse cara virar 60, ele vai ter que ser multiplicado por 12, né? Então vou multiplicar em cima e embaixo por 12. Beleza? Então embaixo, quando eu multiplico por 12, ele
vira 60. Em cima ele vira quem? 48, tá? E esse 1/6 tem que virar 60 também para somar os denominadores. Mas para ele virar 60 eu ten que multiplicar por 10. Então em cima também tem que multiplicar por 10. Soma isso aqui agora dá 58 sobre 60. Essa daqui também é a resposta. Mas nesse caso ele pediu para deixar na forma irredutível. E essa aqui ainda pode ser reduzida mais uma vez. Pedro, como que ela pode ser reduzida? Dividindo por dois em cima e embaixo. Divide por dois embaixo. 30. Divide por dois em cima, 29.
Pronto, agora sim. Tá na forma irredutível. Mas você viu que não tem como errar. Já era a mesma fração, só que tem que ficar na forma irredutível. Tá bom? É, o 29 é primo. Agora, realmente não dá para dividir o 29 por outra coisa, entendeu? É, pode multiplicar por uma outra fração, mas aí tu não vai conseguir somar, né? Porque os denominadores têm que ter ficado iguais. Mas se você quiser manipular só uma delas, você pode. Mas geralmente você tem, acaba manipulando. É, ali em cima eu tava multiplicando só uma delas, né? Então vamos lá.
5/ 9. Vamos lá, galera. 5/ 9 + 3/ 10. Você tá vendo algum múltiplo em comum assim? Fácil? Ah, não tô, cara. Dane-se. Então, multiplica um pelo outro. 9 x 10 90. Agora tu fala assim: "Eu quero que os dois virem 90". Acabou. Quero que os dois virem em 90, tá? Posso já, galera, juntar em um denominador só, já que a gente vai somar os denominadores mesmo e vai só repetir eles. Concorda? Posso deixar assim? Já vou. A invés de eu botar cada fração aqui, ó, o 90 da primeira mais o 90 da segunda, já
vou escrever logo sobre o denominador verdadeiro, tá bom? Eu eu preciso for, vocês estão percebendo que eu preciso forçar vocês a pensarem mais rápido, porque se eu ficar sempre fazendo todo o passo a passo, o cérebro de vocês não vai tem que começar a pegar, né? Então aqui, ó, vou, eu já decidi assim, ó, os dois denominadores vão virar 90. Pronto. Como é que esse cara vira 90? Multiplica por 10. E aqui em cima por 10 também, então virou 50. Como é que esse cara vira 90? Ele multiplica por 9. Então em cima por 9
também. 3 x 9 virou o quê? 27. 77/ 90. Essa é a resposta, tá? Agora, eh, dá para simplificar isso aqui? Dá para dividir eles pelo mesmo número em cima e embaixo, cara? Não, não dá para eu dividir pelo mesmo número em cima e embaixo. Não dá para dividir por três, né? Não em cima e embaixo por três, não em cima e embaixo por sete. Não, não tem. Já está na forma irredutível, tá? É isso aí. 77 também é primo, né? Boa. Tá. Eh, agora 6/ 16 - 3/ 16. muito fácil. O denominador já tá
igual, é 16 mesmo. Então, e 6 - 3 dá o quê? 3. Dá para reduzir isso aqui? Não, já tá irredutível. 8/ 20 - 1 sobre 2. Cara, eu quero muito transformar esse 2 aqui em 20, né? Muito fácil. Para fazer isso aqui virar um 20, eu multiplico por 10 embaixo, em cima. Acabou. Então agora o denominador vai ser 20. E quanto é 8 - 10? É -2. 77 não é primo, não, É isso aí. 77 dá para dividir por 7. Todo é que na hora que apareceu 77, todo mundo falou assim: "7 é primo,
77 é primo." Aí eu eu dou mole de vocês, cara. Dá para dividir por 11? Dá para dividir por um monte de coisa, pô, né, cara? Que eu não posso ficar escutando aluno, cara. Eu passo vergonha. Então, olha só, todo mundo falou ao mesmo tempo, é primo, é primo, é primo. Eu falei: "Ah, é primo, é, eu ainda confio, cara". Pô, olha só, vocês entenderam quanto é 8 men, cara? 8 - 10, eu tenho 8, tô devendo 10, é -2, pô. Agora eu vou fazer o quê? Essa aqui não é a resposta, eu tenho que
dividir por dois em cima e embaixo para ficar irredutível, né? Então, ó, vamos dividir por dois em cima e embaixo. Vai ficar -1 sobre 10. Agora tá irredutível. Agora tá irredutível, tá? Aí já tem gente ali. 77 é primo assim, Claro que não, pô. Então, olha só. Eh, 2/ 10 - 1 sobre 4. Cara, que que eu posso fazer aí? Olha só, que que eu posso fazer para transformar esses dois no mesmo denominador? Ah, Pedro, eh, dá para fazer várias coisas, né? Dá para dá para primeira coisa, dá para eu transformar os dois denominadores em
dois. Concorda? Esse aqui eu consigo fazer ele virar um dois. Eu vou dar meu jeito aqui. Isso aqui é ruim, né? Porque eu vou ter que dividir por dois. Isso aqui vai virar meio, mas dá. E esse aqui também divide por cinco. Mas aí vai ficar tudo zoado, vai ficar tudo estranho. Eu prefiro só o quê? Poderia multiplicar um pelo outro. Eh, 4 x 10 40. Vou fazer os dois virar 40. Posso. Mas eu também posso perceber que ao invés de fazer virar 40, que vai dar certo, eu posso fazer virar 20, porque o 20
tá mais perto. O 20 é um mínimo múltiplo comum entre eles, entendeu? Então, é óbvio, eu posso fazer eles virar em 40, mas eu falo assim, cara, mas o 20 também é múltiplo dos dois, então vou fazer eles virar em 20. Beleza? Então já vou definir aqui que o denominador novo vai ser 20, mas para esse cara, essa fração virar 20 aqui, ela foi duplicada embaixo. Então em cima duplico também para aí o menos preserva. E para essa aqui virar 20, para essa que virar 20, ela teve que ser quintuplicada. Então em cima também você
quintuplica. Quanto é 4 - 5? -1/ 20. Resposta - 1/ tá bom? E essas todas aqui, galera, para somar todas elas, todas tem que estar no mesmo denominador. É claro que você pode fazer primeiro duas, depois duas, depois duas, mas vamos tentar botar todas no mesmo denominador. Quem é um denominador muitíssimo adequado para que todas sejam? 10, pô, porque esse cinco aqui vira 10 fácil e esse dois também vira 10 fácil. Pode ser? Então, tá vendo esse 1/5 aqui? Eu eu trabalho com cada fração individualmente. Como é que eu faço para ele virar sobre 10?
Ele vira 2/ 10. Dobrei em cima e embaixo, tá? Mais o 3/ 10, beleza? Mais 1/ 2, não, eu quero que ele vire 10. Então vou quintuplicar em cima e embaixo. Quintoupliquei em cima, quintupliquei embaixo. Menos o 2/ 10. Perfeito. Repito o denominador. Só isso, né? E agora que eu repito o denominador, eu ataco aqui em cima. 2 + 3 5 + 5 10 - 2 8 8/ 10. Essa é a resposta. Não tem que deixar irredutível. Para deixar irredutível aqui, eu vou dividir por dois em cima e embaixo. Divide por dois em cima vira
4. Divide por dois em baixo vira 5. Tá irredutível. 4/5. Tá beleza? 3/7 - 1/8. Quem eu vou, que que eu vou fazer com eles, bicho? Multiplica logo um pelo outro. 7 x 8 56. Os denominadores vão ser 56. Acabou. Porque os dois vão conseguir virar 56. Tá bom? Como é que eu fiz para esse sete virar 56? Eu precisei multiplicá-lo por 8. Precisei. Então vou ter que multiplicar em cima por oito também. Vai dar 24. Como é que eu fiz para esse 8 virar 56? Eu precisei multiplicá-lo por sete. Então em cima também multiplico
por sete, vai dar sete. Eu estou fazendo, né, o mmc aqui é a mesma coisa, é o mesmo processo que você sempre fez. Eu só não tô, eu só não tô nem fazendo questão de verificar se esse é realmente o mínimo. Ah, esse é o mínimo. Não tô nem esse é o mínimo. Eu tô só botando um múltiplo comum entre eles, tá? Daqui a pouco, e na próxima semana eu ensino a técnica do mmc e onde que ela tem que ser usada. Mas na infração você não tem que perder tempo fazer no mmc, você tem
que já atacar, botar um múltiplo ali plausível, tá show? Então vamos lá. 24 - 7 dá o quê? Nossa, buguei. 17. 17/ 56. O 17 sim é primo, né? E tá na forma redutível. Não dá para eu dividir aqui em cima e embaixo. E não é porque ele é primo, porque se embaixo fosse, por exemplo, um múltiplo de 17, né? Se embaixo fosse 68, aí daria. Se tivesse 17/ 68, eu ia dividir por 17 em cima. Embaixo ia ficar 1 sobre 4. Mas não é 68 embaixo, né? 56. Eu fiquei olhando aqui pro pro 24
- 7, fiquei bugado. Falei que é isso, bicho? Tá. Vamos lá. 25/ 125. Então aqui, ó, 25/ 125 + 1/5. Galera, antes eu posso simplificar só essa fração, né? Eu posso dividir ela por cinco em cima e embaixo, mas melhor ainda, eu posso dividir por 25 em cima e baixo. Então, divide por 25 em cima dá 1. Divide por 25 em baixo dá 1, dá 5. Então, 1/5 + 1/5 já tá com a mesma coisa. 2/5 já tá na forma irredutível. 25/ 125 é a mesma coisa que 1/5, né? Eu tenho aqui uma parte aqui
eu tenho cinco partes. É 1/5. Tá? 3/ 1 + 4/ 1 é 7. 3 + 4 é 7. Pô, sobre 1 não muda nada. 3 dividido por 1 é o próprio 3. Eu, você vê, eu boto as questões aqui para tu realmente pensar, tu falar assim, que que que é isso? Como assim? Porque na hora do Enem toda hora aparece uma questão ridiculamente simples assim que tu fala não é possível. 6/ 11 + 2/ 3. Você fala: "Nossa, Pedro, que que eu faço? 6/ 11 + 2/ 3 bicho". Multiplica um pelo outro e fala: "Olha,
o novo denominador será 39. Como é que eu fiz para esse cara virar 39? Eu precisei triplicá-lo. Então triplica em cima também. 18. Como é que eu fiz para esse denominador virar 39? Eu precisei multiplicar por 11. Então multiplique por 11 em cima também. 2 x 11 dá 22. 18 + 22 dá 40/ 39. Acabou. Tá na forma irredutível. 33, né? Tô viajando aqui com esse 39. Eu errei aqui. Eu fiz e olha só. 6 x 11 + 2/3 eu multipliquei 3 x 11, eu falei 39. Eu tava pensando em 33, cara. Tá, é 33
aqui. Como é que eu fiz para esse cara virar 33? Eu precisei, não é, eu não comi direito hoje, não. Tô perguntando onde combina. Como é que eu fiz para esse 11 virar 33? Eu tripliquei ele. Então triplica em cima também. Você vê que eu tava fazendo, eu tava agindo como se fosse o 33, né? Só escrevi o 39. Como é que eu fiz pro 3 virar o 33? Eu multipliquei por 11. Multiplica por 11 em cima também. Então dá 40/ 33. Tá irredutível. Não dá para dividir eles dois pela mesma coisa. Tá bom. Todo
mundo tá falando, né? São as 4 horas de sono. Isso mesmo. 6/ 7 + 1/ 4. Quero nem saber. Vou transformar os dois em 28. Ah, vai ser 28. Pronto. 7 x 4 é 28. Para esse cara virar 28, ele precisa ser quadruplicado. Quadruplica em cima também. Para esse cara aqui virar 28, ele precisou ser sextuplicado. Então, eh, ele precisou ser, na verdade, se duplicado, né, para ele virar 28. Então, multiplica por 7 em cima também. 24 + 7, 31/ 28. Tá irredutível. Vamos lá. 12/ 36 + 2/3. Esse 12/ 36 eu já vejo ele
como 1/3, né? que ele tem aqui 12 e ele tem aqui o 36, que é o triplo dele, né? Então uma coisa dividida pelo seu triplo é 1/3. Divide por 12 em cima vira 1. Divide por 2 embaixo vira 3. Fica o quê? 3/ 3 que dá 1. 6 - 7/ 21. Aí você olha e fala assim: "Cara, qual vai ser o múltiplo comum deles?" Cara, tanto faz. Multiplica um pelo outro. 6 x 21 dá o quê? 6 x 20, 120. 6 x 1, 6, 126. Concorda? Então aqui, ó, muito fácil. 126. Como é que
eu fiz pro se virar 126? Ué, você não lembra? Pro seis virar, pô, é verdade. A menina ali falou o negócio, né, certo. Ela falou assim: "Por que que você não bota aí 42, né?" É mesmo, né? Tá certo. Eu tô com sono, eu tô menos peixe picaz, né? Mas é isso mesmo, né? Eu posso colocar aqui o 42, tá certo? Tá. O 42 é um múltiplo de dois, né? Claro. Eu vou terminar de fazer assim só para É, tão perguntando? Eu dormi hoje umas 3 horas meia, 4 horas e foi numa cadeira. Então, olha
só, é visível, né, que eu fico eu fico mais mais Então, olha só, mas só para vocês visualizarem aqui, tá bom? Como é que eu fiz o 6 virar 126? Eu multipliquei ele por 21. Multiplica por 21 em cima também. 4 x 21 vai dar 84. E aí o 21 para ele virar 126, ele foi multiplicado por 6. Então aqui vai dar 42 em cima. 84 - 42 dá 42/ 126. Agora eu tenho ainda que simplificar, né? ficou bem mais trabalhoso, tá? Divide aqui em cima, ã, cara, divide por 2 vira 21 e divide por
2 também vira 63. Agora, divide por 3 vira 7, divide por 3 vira 21. Divide por 7 vira 1. Divide por 7 vira 3, vira 1/3 no final das contas. Mas se eu tivesse já começado melhor, né? Se eu já tivesse aqui, ó, visto assim, olha, 4/6 - 7/ 21. Primeiro que eu posso começar simplificando as frações, né? Óbvio. É, então aqui, ó, tá vendo esse 4/6? Eu vou dividir por dois em cima e embaixo. Beleza? Então virou 2/3. Tá vendo? Agora esse 7/ 21, vou dividir por 7 em cima e embaixo. Virou 1/3. Então
ficou ali 2/3 - 1/3. Ficou 1/3. 2 - 1 é é 1 1/3. Tá bom? Estamos indo. Certo. Então aqui, ó, 1/3 é a resposta. Vamos mais. Agora é molezinha, né? Agora é tudo multiplicação e divisão, né? Então vamos nessa. Bora lá. Aqui, ó, primeiro ali, ó, 4/5. Vou fazendo aqui embaixo como se fosse um rascunho. 3/5, galera, multiplico de cima pelo de cima, de baixo pelo de baixo, independente de tá igual, não muda nada, tá? Eh, então o que pode fazer também é você sem o que que qual que é o macete aqui? É
você visualizar que tudo aqui tá no mesmo traço, né? É como se fosse assim, ó, 4 x 3/ 5 x 5, que aí se tu quiser simplificar alguém, você pode, tá bom? Só para deixar isso claro aí que a gente pode usar essa técnica também, tá? Então, vamos lá. 4 x 3 eu sei que dá 12 e 5 x 5 dá 25. Já tá na forma irredutível. É, já está na forma redutiva. Sim. 1/5 x 79 1 x 7 e 5 x 9 45. Tá irredutível. Vamos lá. Vou fazer assim direto, tá bom? 3 x
2 6 e 10 x 5 não tá irredutível, tá? Mas deixa, galera, eu vou fazer assim só para mostrar pra galera, porque eu acho que vai ter gente que vai ter dificuldade se eu fizer direto assim, tá bom? Então vou fazer assim, ó. 3 x 10 x 2/ 5, tá bom? Aí eu vou fazer aqui 3 x 2 que dá 6 e aqui dá 50. Agora eu vou dividir os dois por 2, porque eu tô vendo que dá, tá? Então divide por dois aqui dá o quê? 3 e divide por dois aqui dá o quê?
25. Agora sim, 3/ 25 é a forma irredutível, tá? Mas eu poderia com certeza ter feito essa simplificação antes, né? Eh, isso só dá para você simplificar uma fração quando tanto numerador quanto denominadores são simplificáveis pelo mesmo número, ou seja, eles compartilham algum divisor. Compartilham algum divisor. Concorda? O 6 e o 50 compartilham qual divisor? O dois. Então, divido por dois em cima vira 3, divido por dois embaixo vira 25. Só que eu poderia ter feito isso antes, né? Eu poderia ter pegado aqui o 2 e o 10 e dividido por dois, ó. Divido por
2ra 1, dividido por 2ra 5. Aí fica só 3 sobre 25. Do mesmo jeito. Só queria mostrar isso, né? Que você pode fazer antes ou depois. Vamos lá. 8/ 12, ó. 8/ 12 x 4/ 6. Eu posso fazer 8 x 4 32 e 6 x 12 72. Dividir em cima, embaixo por 2. Aí vai virar 16/ 36. Aí divide por 2, vai virar 8/ 18. Aí divide por 2, vai virar 4/ 9. Posso, mas eu também poderia ter feito as simplificações antes, né? Eu poderia ter aqui, eu tenho liberdade de simplificar tanto esse 8 com
esse 12, quanto esse 8 com esse seis aqui, quem tá em cima com quem tá embaixo, né? Então aqui, ó, vou já vou começar dividindo por quatro em cima e embaixo. Mas quem? Vou dividir esse cara por quatro e esse cara por quatro. Beleza? Dividiu por quatro, virou um. Dividiu por quatro, virou três. Agora eu vou pegar esse oito e esse seis, vou dividir eles por dois, tá bom? Dividiu aqui por dois, virou 4. Dividiu por 2, virou 3. Pronto, ficou 4 em cima sobre 3 x 3, 4 sobre 9. Acabou. OK? 12/ 36 já
vou escrever 1/3, já vou dividir por 12 em cima e embaixo é 1/3 vezes 24/ 72 é 1/3 também porque eu sei que o 24 o 72 é feito disso de 24 + 24 + 24. Então se eu dividir por 24 aqui vira 1 e por 24 aqui vira 3, tá? Agora 1 x 1 dá 1 sobre 9 de novo. 1 sobre 9. Bacana, né? 7/ 12 x 8 x 36. Vamos lá. X/ 36, né? Então 7/ 12 x 8/ 36. Cara, eu vou vou simplificar aqui esse 8 com esse 12, tá bom? Vou dividir
os dois aqui por quatro. Então, dividiu aqui por 4, virou 2. Dividiu por 4 aqui, virou 3. Agora esse 2 e esse 36 eu vou simplificar. Dividi por 2, ele virou 1. E dividi por 2, ele virou 18. Fiquei com 7. E embaixo tem aqui o 3 x o 18. Quanto é 3 x 18? 3 x 10 30. 3 x 8 24. 7/ 54. essa resposta. OK. Beleza. Vamos lá. Agora é uma divisão, né? Como é que é uma divisão? 13/ 4 dividido dividido. Eu coloquei a resposta no lugar errado. Ah, tá. Botei para baixo,
né? Ah, tá. Tô viajando. Já entendi. Essa 7 sobre 54 é a de cima, né? É isso aí. O 7/ 54 tá aqui em cima, né? Tá. Agora sim. Vamos lá. 1 sobre 8 dividido por 2 sobre 9. Como é que faz divisão de fração? Repete a primeira e multiplica pelo inverso da segunda. Repete a primeira. Então, e o inverso da segunda é o quê? Emés de ser 2/ 9 é 9/ 2, viu? O 2/ 9 virou isso. Virou 9/ 2. Agora eu multiplico normalmente, já tô fazendo a divisão, tá? Então 1 x 9 dá
o quê? 9. E 8 x 2 dá o quê? 16. Dá para simplificar? Não dá. Eu não consigo dividir eles por um número igual. Eles não têm os mesmos divisores aqui, tá bom? Então fica aqui, ó, 9/ 16. Entendido? 13/ 4 di por 1 sobre 2. Dividiu uma coisa por meio, você tá dobrando essa coisa, né? Então já poderia dizer que aqui vai ficar o dobro 26/ 4. Mas vamos lá. Repete a primeira pelo inverso da segunda. O inverso da segunda é isso aqui. 13 x 2. Antes eu vou simplificar o 2 com 4, tá
bom? Então aqui, ó, simplifica o 2 dividido por 2 e aqui também fica 13/ 2, OK? 4/5 di por 1/ repete a primeira pelo inverso da segunda. O inverso da segunda é isso aqui. Esse um aqui embaixo nem precisa, né? Vamos lá. Vou simplificar aqui o 5 e o 10, tá bom? Vou dividir por 5 os dois. Divide por 5 vira 1. Divide por 5 vira 2. Quanto é 4 x 2? 8. Essa é a resposta. 3/7 div por 1/4. Tá bom? Repete a primeira pelo inverso da segunda. O inverso da segunda é isso aqui.
3 x 4 12. 3 x 4 12/ 7 12/ 7 não tem o que fazer. Já tá irredutível. Beleza? Ainda depois dessa aqui a gente tem mais essa aqui. Essa aqui é sobre número misto. Tá bom, galera? É muito importante saber número misto. Tem aulas já extensas sobre número misto, com muito exercício de número misto. Vocês têm que assistir. Vocês t que assistir. Mas eu já vou dizer, o número misto, ele não é uma multiplicação, tá bom? Isso aqui não é 1 x 1/4. O número misto é sempre 1 e também 1/4. É 1 +
1/4. Quanto é 1/4 de alguma coisa? Da mesma forma que 1 sobre 2 é 1/4 é 0,25. Então isso aqui eu já sei de cara que é 1,25, né? que tem uma coisa inteira e também além de ter uma coisa inteira tem uma coisa fracionária. Então é um inteiro e mais 1/4 que é 0.25. Beleza? Mas qual é o método bonitinho do número misto? Tá? Tu tem 1 e 1/4. Não é 1 x 1, tá? Não é não é isso aqui, ó. Não é isso. Isso aqui é multiplicação de fração, tá? Número misto é 1
e também tem 1/4. É 1 e 1/4, tá? Beleza? Quanto que é isso aqui, ó? Isso aqui é um número misto, ó. 3,5. Isso aqui é o quê? 3,5. É exatamente isso, tá, Pedro? Pode somar. É isso mesmo. Número mista para você somar é 1 + 1/4. Acabou. Se você quiser fazer do jeito super bananada, seguro, tu vai olhar o número misto, vai sempre somar. Tu vai falar assim: "Então é 1 1 sobre 1, né? Porque ele tá um inteiro + 1/4." Sim. Aí esse denominador tem que virar quatro. Faz ele virar quatro, então. E
multiplica por quatro aqui em cima também. Agora mesmo denominador. 4 + 1 5. Pronto. 5 4 divide 5 por 4. Divide por 2 dá 2,5. Divide por 2 1,25. É o que eu tinha falado. É 1 e 1/4 1.25. Sacou? Pegou. Então, e a forma assim que eu acho, eu não gosto tanto dessa forma, mas os professores fazem é o quê? é você fazer esse aqui vezes esse. 4 x 1 4 mais esse aqui que dá 5 e mantenho o mesmo denominador. Eu não curto muito. Eu curto ou somar ou enxergar. Se eu souber o
número misto. Eu sei que 1/4 é 0,25, então já boto 1,25, tá bom? Então aqui, ó, reescreva eles na forma decimal e fracionária. Ele quer os dois. Vamos lá. Forma decimal 1,25. Forma fracionária 5 sobre 4. Como é que eu chego na forma fracionária? Eu tenho aqui 1 e 1/4. 4 x 1 4 mais esse aqui 5. E boto no mesmo denominador 5 sobre 4. E para chegar na forma decimal eu teria que dividir o 5 pelo 4. 5 dividido por 4 1.25. Tá bom? Vamos lá. Eu tenho 3 e 2/4. Pô, 2/4 é cara.
2/4 é maior coisa que meio. Eu tenho 3,5 aqui. É 3,5. Sacou? E como que eu faço uma fração que dê 3,5? Pô, 7/ 2. 7/ 2 dá 3,5. Você tem que tentar chegar nisso de cabeça também. 7 por 2 dá 3/5. Mas vamos fazer o métodozinho tradicional. Vamos lá. Eu tenho 3 e 2/4. 4 x 3= 12. 12 + 2 14. Repete o mesmo denominador. 14/ 4. Simplifica, divide por dois em cima e embaixo. Então divide por 2 em baixo fica 2. E aqui fica 7/ 2. É aquela coisa que eu te falei. Quanto
que dá agora de fato 7/ 2? 7/ 2 dá 7/ 2 3,5. Então aqui é a resposta. Forma decimal 3,5, forma fracionária 7/ 2. Sacou? Não, pô. O número ele sempre vai ser somado, não vai ser subtraído nunca, não. O número misto é isso aqui, tá? Vamos lá. 8 e5. Pô, galera, 8,5 8,5. Aí eu posso fazer, né? 2 x 8 16 + 1 17/ 2. É isso aí. Mas eu também consigo chegar aqui. 17 por 2 dá 8,5, né? 16 por 2 dá 8, né? Então você bota mais unzinho, tá? 9 e 1/6 aqui
já é um pouco mais difícil, mas isso aqui 1/6 eu já sei de cabeça que é 0,16, tá? Então é 9 mais isso aqui. Vamos lá, vamos fazer a forma e fracionária dele. 6 x 1, 6 x 9 + 1, 55. E aí sobre o mesmo denominador que tava 55/ 6. Aí agora se você dividir 55/ 6 você vai achar a resposta. Ó, mas 54/ 6 dá 9. Só que tem mais um para dividir por 6. Esse 1 por 6 dá o quê? 0,16. Vamos colocar assim aproximadamente 9,16. E 3 e 1/3. Fala sério, 3
e 1/3 tem que dar 3,33, né? 1/3 é isso. Como é que é 1 por 3? É 0,33. E a forma fracionária de uma coisa que dê 3,33, deve ser 10 dividido por 3, né? Cadê 3 x 3? 9 + 1, 10 sobre o mesmo denominador. É isso mesmo. Você viu? Eu tenho a noção de qual fração vai dar aquela ali. É isso que eu quero que você tenha. Tenha a noção, porque isso aí vai fazer você ficar muito mais rápido, tá? 7 e olha, olha o número tá na tua frente. 7,5. 7,5. Qual é
a forma fracionária disso aqui, bicho? Pega esse número aqui, tu duplica ele. Duplica ele. Ah, vou duplicar ele. É, vai virar 15. É, Pedro, mas todo número tá sobre um, né? É. Então, se tu duplicar em cima, tu duplica embaixo também. Também funciona assim. 3 e 3/4. Quanto que é 3/4? De quatro coisas tu tem três, tu tem 0.75. 3/4. É isso. No módulo de porcentagem vocês vão pegar melhor. Então, se que é 3,75. Para eu atingir um 3,75, sei lá, vamos duplicar o 3,75. Quando duplica, ele vai virar o 7,5. Duplica de novo, vai
virar o 15. Então vai virar o 15/ 4, né? Porque eu dupliquei, dupliquei 15/ 4. Agora, claro, se preferir 4 x 3, 12 + 3, 15 sobre o mesmo denominador, 15/ 4. Você entendeu? Você não pode saber número misto, mas de uma maneira muito mecânica e misteriosa. Tipo, eu só consigo fazer se eu fizer esse procedimento aqui, se eu preciso fazer esse vezes esse mais esse. Senão, número misto tem que ser uma coisa manipulável, uma coisa que você sabe fácil, tipo, pô, é óbvio, ninguém tem dúvida do que que é o três. Ó, o três
é o três, o quatro é o quatro, o cinco é o cinco. Aí o número misto, não, tem que ter, tem que ter todo um cuidado com o número. Número misto é fácil, pô. 5 e 3/4, 5,75. Duplica o 5,75, vai dar 11,5. Duplica de novo, vai dar 23. Pronto, dá 23. E tu duplicou e duplicou, então 23/ 4. Agora 4 x 5, 20 + 3, 23. Sobre o mesmo denominador, 23/ 4 também funciona. Divide 23 por 4, vai dar 5.75. 9 e 2/3, ué. 9,66. 2/3 é 066. 1/3 é 0,33. Um monte de gente
errou essa na prova descendo. Um monte de gente. Um monte de gente errou. Tá. número misto. E aí, como é que eu descubro a forma fracionária, né? 3 x 9 27 esse 2 aqui dá 29 sobre o antigo denominador, 29 sobre 3. Como é que eu faço 1 sobre 6 mentalmente? Tá, vamos lá. Dividir por 6 é você dividir por 2 x 3. Você concorda? Divide 1 por 3. 1 por 3 dá 0,33. Agora divide esse 0,3 pelo 2, que foi o que faltou, né? Se fosse 0,32 não daria 0,16. Se fosse 0,32, mas não
é 0,32, é 0,33. Então dá 0,16 e ainda 5 milésimozinhos ali, sacou? Então vocês estão entendendo? Esses números todos eu já sei quais são. Eu tô, você tem que saber que 2/3 é 06, mas como é que eu sei disso? É o que você tá fazendo agora. Só de você estar numa aula em que o professor fica tratando isso como se fosse uma coisa normal, tu já tá no lugar certo. Eu tô justamente, eu tô tratando aqui como uma coisa banal. Saber que o 2/3 eu falo 2/3 é 0,66. É óbvio. Aí tu tem que
falar pro teu cérebro 2/3 é 066. E tu vai ver que tu vai começar a ficar muito fera por causa disso, tá? 8 e 1/4. 1/4 é 0,25, pô. Então é claro que isso aqui é 8,25, só que todo número ele tá sobre um. Então se eu quiser ver a forma fracionária, eu posso começar a multiplicar aqui até ele ficar fechado. Se eu dobrar, ele vai virar 16,5. Não tá fechado. Se eu dobrar de novo, vira 33, tá? Então ele vai virar 33. Mas para isso acontecer, ele precisou ser dobrado e dobrado. Então 33/ 4
é a mesma coisa que esse cara aqui. Mas se eu pegar 4 x 8 32 + 1, 33 e mantiver no mesmo expoente, 33/ 4 também ajuda, também dá a mesma coisa, tá? Tá resolvido aqui. Ah, professora, blá blá blá. O jogo, esse estudante respondeu a pergunta, quais são as posições? O que que ele quer? Ele quer eh em quais posições estão os números iguais, os números que são idênticos, tá? Tão pedindo a cada questão 16. Cadê? Ó, 25/ 125 é uma fração, concorda? Eu vou eu vou simplificar ela por 25 em cima e embaixo,
ó. 25 por 25 dá 1 e 125 por 25 dá 5. Isso aqui é 1/5 + 1/5. Repete o denominador que é 5 e soma 1 + 1 dá 2. Tá bom? Vamos lá. Isso aqui é ridículo. Isso aqui é muito moleza. Ele quer saber aqui, ó. Encontre três quantidades iguais. Três quantidades iguais. Vamos lá. Isso aqui é o quê? É quatro, galera. Tem coisa aqui que quem tá chegando agora não sabe ainda. Eu já expliquei em outras aulas da plataforma. Eu peço que você tenha paciência, tá bom? 4 elevado 1/ 2. Semana que vem
eu vou mostrar isso, beleza? Mas eu já botei aqui agora. Como, por favor, semana que vem vou mostrar isso, mas só para você ter aqui uma noção, tá? Quando você tem um número elevado a 1 sobre 2, 4 elevado a 1/ 2, você tem que pegar esse denominador e puxar para fora como uma raiz. Ó, tu pega o denominador e faz assim, ó, puxa como uma raiz, ó. Puxa para cá como uma raiz. Então, por exemplo, aqui, ó, tá vendo? Quatro, esse dois vai para fora e o um aqui não muda nada. Então, pronto. 4
elevado a 1 sobre 2. Você pega o doizinho aqui do denominador e, ó, puxa para fora como a raiz. Quanto é agora a√ quadrada de 4? É 2. Então, na verdade, quanto vale esse cara aqui? O valor desse primeiro aqui é dois. Ele quer os três iguais. Número misto. 4,5. 4,5. 10/ 45. Pô, menos do que 1/4, né? Porque se fosse 10 div por 40 daria 1/4. Então isso aqui deve dar uns 0.25 para menos, sei lá, né? Não, o número elevado a 1 sobre 2 não é metade sempre, não. Claro que não. Se eu
tiver pô 9 elevado 1/ 2, como é que como é que eu faço? Eu poo dois para fora, vai ficar o quê? √ qu 9. Isso aqui é 3, concorda? Um número elevado a 1 sobre 2, ele sempre é a própria raiz quadrada. Aí sim você pode dizer, tá? Eu quero achar os três que são iguais aqui, galera. Então não vou ficar perdendo tempo. Tá vendo esse 4,5 aqui? Ó aqui, ó. Eu já tenho aqui um 4,5. Agora eu acabei de achar outro 4,5. Esse 4 di por 5 é 0.8. E o 18/ 4, divide
18 por 4, você vai dividir por 2 por 2. 18 por 2 9. E 9 por 2, 4,5. Cadê as posições iguais? Tá no slot 2, no 4 e no 5. Olha que questão banal. Olha que que tragédia errar isso aqui na hora da prova. Que leira serrar isso aqui na hora da prova, né? Aqui, ó. Ele quer sabe o quê? Quantas cartas da mão podem formar um par com a carta da mesa? Ó, a carta da mesa tá aqui. Quantas aqui para formar um par tem que ser igual, tá bom? Quantas são iguais a
essa aqui, ó? Isso aqui é 6/ 8. Você já tem que visualizar o seguinte: 6/ 8 é o quê? 6/ 8 é a mesma coisa, ó. Simplifica em cima e embaixo por 2 que 3/ 4. E 3/ 4 é o quê? É 0.75. Ó, divide o 3 div 3 por 4, ó. Divide por 2, dá 1,5, divide de novo 0.75, tá? Então, e a mesma coisa que 75%, né? Por quê? Porque, ó, ó, vamos lá, deixa eu mostrar aqui bem detalhadamente. Tá vendo? A carta que ele deu é 6/ 8. Eu já falei, olha, é
a mesma coisa que 3/ 4, porque eu dividi por dois em cima e embaixo. Então é a mesma coisa. Agora, se eu executar a divisão do 3 por 4, dá quanto? 0.75. É a mesma coisa. O tá sobre 1, né? Porque todo número que não tá sobre ninguém tá sobre um. Posso multiplicar por 100 em cima e embaixo? Posso. Multiplica por 100 em cima. 75 e por 100 embaixo? 100. Como é que eu chamo uma coisa que tá sobre 100? 75%. Esse símbolo do porcento, ele significa dividido por 100. Acabou. Todo mundo aqui é idêntico.
Todos os que estão aqui são idênticos. Ah, Pedro, e se tu dobrar aqui e dobrar embaixo? 12/ 16 também é idêntico isso aí, sacou? Então, vamos lá. Quais são as cartas que são idênticas a essa aqui, ó? Aos 6/ 8. 75%. Sim, é idêntico. 75% é a mesma coisa que 75. Troca o por sobre 100. Pronto. Divide por 25 em cima e embaixo. Vai dar 3 aqui e vai dar 4 aqui. 3/ 4. Não tem nada a ver. Todos esses, essa carta aqui ela é menor do que 1. 8 é menor do que 1. Tanto
que dá 0.75. 75% é menor do que 1. Tanto que 75% não é uma coisa inteira, é só 75%. 3/ 4 é menor do que 1. Tudo é menor do que 1.4 já é bem maior do que 1. 34% não tem nada a ver. 34/ 100. 0,75 é a mesma coisa. 75% do difizer a divisão dá 0.75. 4,3 não tem nada a ver. 7,5 não tem nada a ver, é bem maior. 4/ 3 não tem nada a ver, é maior do que 1. 4/ 3 dá 1,33. 6,8 não tem nada a ver e 3/4 é
a mesma coisa. São três as cartas que podem formar um par. Primeira semana do ciclo de nivelamento concluída. Beleza? Parabéns a quem assistiu e vamos nessa. Assistam todas as aulas que tiverem aqui, tá bom? Ajuda do alfabetização matemática principalmente. Agora sim, chegou o grande momento de aprender mmc e MDC, tá bom? Isso é importantíssimo. Isso aqui é uma coisa absurda, cai bastante na prova. Esse raciocínio você tem que dominar. Isso aqui que vai fechar mesmo a nossa aula de fundamentos aqui. Fundamentos dos fundamentos da matemática básica da básica, tá bom? Cai dentro. Então vamos nessa.
Sejam todos bem-vindos a mais uma aula da plataforma SAD. Hoje a gente vai fazer uma aula aqui completa sobre mmc e MDC, né? os dois posicionados lado a lado. Eu vejo que esse é um assunto que e o tempo passa e continua gerando muita muitas dúvidas, né, nas pessoas, até mesmo nos alunos de autodesempenho. Eh, vez ou outra aparece no Enem uma questão que exige conhecimento ou de MMC ou de MDC. E ela, primeira coisa, né, nunca na história da humanidade, nunca na história da prova do Enem foi cobrada uma questão no Enem, nunca que
dissesse calcule o mmc desses números ou calcule o MDC desses números. Isso nunca aconteceu, nunca, tá? Eh, mas já caíram várias questões que você precisava calcular o MMC ou que você precisava calcular o MDC. E a questão nunca fornece nenhum tipo de pista disso. A questão nunca fala mmc, nem fala MDC, nem mesmo fala divisor e nem mesmo fala múltiplo, tá? Então a interpretação é sempre uma interpretação ã sutil, é sempre uma interpretação em que você precisa mesmo estar familiarizado com a questão para acertar. Outra coisa desse tipo de questão, tá? questão de MMC e
MDC. Essas questões têm um padrão. Se você domina muito MMC e MDC, você sempre vai conseguir fazê-las e sempre vai conseguir fazê-las rápido, sempre vai conseguir fazer rapidamente. E se você não domina MMC e MDC, você também vai conseguir fazer, só que você vai demorar uma eternidade. Esse é o padrão dessas questões. E esse isso é o tipo de questão bem complicado, então, né? Porque se você não sabe a matéria, esse é o problema, que você não vai saber a matéria, mas você vai conseguir fazer a questão desde que você fique nela muito tempo, tendo
muito trabalho. Então é uma questão que rouba muito tempo para quem não tá eh proficiente na matéria. Beleza? Então é isso aí que eu que eu queria dizer para vocês na introdução da aula. Então, por isso que eu eh vejo a necessidade de ter essa aula, tá? Vamos lá, começando aqui pelo MMC, porque a gente já teve aula de MMC aqui, aula específica de MMC, né? O que que é o MMC? é o mínimo múltiplo comum, tá? Então, primeira coisa, o que que são múltiplos de um número? Vamos supor que eu tenho aqui o número
quatro. Quem são os múltiplos do número quatro? Os múltiplos do número quatro são nada mais nada menos do que os resultados de eu pegar o número quatro e começar a multiplicar por vários números, tá? Então, o que que acontece se eu multiplicar o número 4 pelo zero? É, se eu multiplicar o 4 pelo zero, dá 0. E se eu multiplicar o 4 pelo 1, dá 4. E o 4 pelo 2 dá 8. E se eu multiplicar o 4 pelo 3, dá 12. E o 4 * 4 dá 16. Se eu multiplicar aqui o 4/ 5
dá 20, ou seja, é a tabuada do 4, é o resultado de eu multiplicar o 4 por um número inteiro. Acabou. Por um número eh, por um número inteiro a gente vai obtendo isso. Então, 0, 8, 12, 16, 20 e por aí vai. A gente vai tendo 24, a gente vai tendo 28. Esses são os múltiplos, ou seja, os múltiplos são infinitos. Já começa por aí, tá? Os múltiplos são infinitos, tá? E quando eu pergunto para você eh o que que é o mínimo múltiplo comum? Então, primeira coisa, você já entendeu o que que é
múltiplo, tá? Eh, e mínimo múltiplo comum só pode existir entre pelo menos dois números. Não tem como ter múltiplo comum, porque comum quer dizer o quê? Que os dois têm. Então, olha, eu e você temos muito em comum, nós dois temos muito em comum. Comum tem que ser duas coisas ou mais, né? Eu, você e ela temos muito em comum. Então, nós três temos muito comum. Então, mmc só existe entre dois números ou três números ou quatro números ou entre cinco números ou mais. Beleza? OK? O que significa quando eu pergunto qual é o mmc,
qual é o menor múltiplo comum que existe entre o 4 e o 7? Eu tô querendo saber primeiro alguma coisa sobre os múltiplos do quatro e os múltiplos do sete, né? Então os múltiplos do quatro, quatro, lembra? 4 8 12 16 e assim vai. E os múltiplos do 7, quem seriam os múltiplos do sete? 7, 14, 21, 28, 35 e assim vai. Agora eu quero saber um múltiplo que seja comum aos dois. Então que os dois tenham aquele múltiplo, tá? E eu quero que ele seja o menor possível. Vamos estruturar isso um pouco mais. Vamos
pensar aqui no número quatro e vamos pensar no número sete. E vamos pensar agora nos múltiplos de cada um deles, tá bom? Vamos lá. Quem são os múltiplos aqui de quatro, né? Tirando o zero, não vou considerar o zero aqui para nenhum dos casos, tá bom? A gente tá falando aqui dos dos números que que não são nulos. Então vamos lá. Os múltiplos do número quatro. Primeiro o próprio quatro, óbvio, porque 4 x 1 dá 4, depois 8, depois 12, depois 16, depois 20, 24, 28, 32, certo? 36 e assim por diante. Quem são os
múltiplos? do número sete, então o próprio sete, né? Porque 7 x 1 dá 7, depois 14, depois 21, depois 28, depois 35, depois 42, 49 e assim vai. Você tá identificando algum múltiplo que seja comum aos dois? É, eu tô, por exemplo, aqui, ó, o 28. O 28 é múltiplo dos dois ao mesmo tempo, né? O 28 ele é um múltiplo comum. Agora, o 28 é o menor múltiplo comum deles. Sim, o 28 é o menor múltiplo comum. O 28 é múltiplo dos dois ao mesmo tempo, ou seja, ele é um múltiplo comum e ele
também é o menor deles. Não tem outro aqui múltiplo deles que seja eh não tem outro músculo que seja menor, por exemplo. Então já tem a resposta, né? O mmc entre 4 e 7, o mínimo músculo comum é o 28, tá? Agora vamos lá. Qual é o mmc entre 3 e 4? Vamos primeiro pensar nos fazer da mesma forma que a gente fez antes. Vamos pensar apenas nos múltiplos aqui. Então, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33 e por aí vai. E do 4 a gente tem aqui 4, 8, 12, a
gente tem 16, 20, 24, 28, a gente tem 32, a gente tem 36. Aqui depois do 33, a gente também teria 36. Então, vamos lá. Me fala múltiplos comuns entre o 3 e o 4. É, o 36 é um múltiplo em comum. Os dois têm esse múltiplo, né? Os múltiplos são infinitos, né? Porque os múltiplos eles vão crescendo para cima. Os dois têm 36. Maravilha. Tem outro múltiplo comum que você tá vendo? É o 24 é um múltiplo comum aos dois. Beleza? Ótimo. Ah, tem outro múltiplo em comum que você esteja vendo aqui? Tem. O
12, por exemplo, ele é múltiplo dos dois ao mesmo tempo. Maravilha. Agora, qual desses é o menor múltiplo comum deles? O menor múltiplo comum é o 12, tá? Embora o 24 também seja um múltiplo comum, embora o 36 também seja, tá? Isso é mmc. Qual é a utilidade prática disso? A utilidade prática disso no Enem, eu vou já resumir, é principalmente em coisas de caráter cíclico. Pode anotar isso, pode mentalizar isso. Coisas de caráter cíclico. OK? Então vamos lá. Como assim, Pedro? Coisas de caráter cíclico. Sim. Vamos lá. Eu sou um médico, você é um
paciente e eu falei para você o seguinte, galera, tem gente perguntando se a aula é gravada, se aula viu, porque apareceu aqui uma data 9 de janeiro na tela aqui. Meu iPad tem essa, não sei por que meu iPad tá sempre com essa data 9 de janeiro. Eu tenho que atualizar alguma configuração dele, tá bom? Mas eu estou aqui ao vivo com vocês, tá bom? Hoje é dia 10 de janeiro de 2025, tá? São 10:55 da manhã. Então vamos lá. Eh, eu sou um médico e eu prescrevi para você dois fármacos. Eu falei assim: "Olha,
você vai tomar aqui o fármaco A e você vai tomar o fármaco B". São dois remédios que você vai ter que tomar, tá? Esse primeiro fármaco aqui, tu vai tomar de três em três horas. A cada 3 horas você vai tomar. E o segundo fármaco, tu vai tomar de quatro em 4 horas. Ou seja, vamos começar a contar a partir de meia-noite, beleza? Então, agora é meia-noite, eu vou te dar os remédios ao mesmo tempo. Então, vou ministrar para você aqui agora os remédios simultaneamente, beleza? Tá todo mundo entendendo, né? meia-noite agora eu vou te
dar esses remédios aqui ao mesmo tempo. E aí, é claro que eu te dei os remédios aqui meia-noite. E aí, quando que você vai tomar o remédio A? 3 da manhã de novo, né? Depois de tomar meia-noite. Quando que você vai tomar o remédio B? 4 da manhã. Você vai tomar o remédio B, certo? Depois você vai fazer o quê? Tomou o remédio A às 3 da manhã, vai tomar às 6 da manhã, às 9 da manhã, vai tomar meio-dia, vai tomar 3 da tarde e assim vai. E o remédio B você vai tomar quando?
Vai tomar 4 da manhã, depois 8 da manhã, depois meio-dia, depois 4 da tarde e assim vai. E eu te pergunto assim, ó, tirando agora, né, que é meia-noite, eu acabei de te dar o remédio, qual é o próximo horário em que você vai tomar os dois remédios ao mesmo tempo? Qual é o próximo horário? Ou seja, eu quero o menor horário em que você vai encontrar os dois remédios juntos, certo? Você teria que descobrir o menor múltiplo comum. Por quê? Vamos lá. Porque é fato que você só vai tomar esse remédio aqui nos horários
múltiplos de três. Claro, considerando que você começou meia-noite, né? Se você começar 1 da manhã, você vai tomar esse remédio aqui quando? Às 4 da manhã, depois às 7 da manhã, né? Então sempre vai ter que levar em consideração o horário em que você começou, né? Claro. Mas eu quero dizer, você só vai tomar o remédio A de três em 3 horas e só vai tomar o remédio B de quatro em 4 horas. Então se então ou seja, é fato que você vai tomar esse remédio sempre em múltiplos de três ou em múltiplos de quatro.
Mas eu quero saber quando você vai tomar os dois. Então eu preciso de um número que seja múltiplo de quem? Do três e do quatro. Seja múltiplo em comum dos dois. Mas eu quero o menor deles porque eu quero saber qual é o próximo horário. Você tá vendo? É só para você entender. Olha o tempo que eu tô levando para para explicar mmc. Olha como eu tô que para você entender que isso aqui que é o diferenciado para você tem que focar muito em entender a tradução do conceito de mmc, a tradução. Então dizer qual
é o próximo horário em que você vai tomar esses remédio juntos. Isso quer dizer o quê? O menor múltiplo comum, porque é o próximo horário. É claro que você vai tomar esse remédio ao mesmo tempo, A e o B, a meio-dia, mas é claro que você vai tomar também na próxima meia-noite. É claro que você vai tomar esse remédio várias vezes junto, mas quero saber o próximo horário. Então vamos lá. Qual que é o MMC entre o três e o quatro, né? Vamos, se a gente fosse calcular aqui manualmente, né? Ah, tu vai tomar esse
remédio aqui de três em 3 horas. Ou seja, você e começou tomando meia-noite, você vai tomar 3 da manhã, depois você vai tomar 6 da manhã, depois vai tomar 9 da manhã, depois vai tomar é meio-dia, depois vai tomar 3 horas, depois vai tomar 18 horas, depois vai tomar 21 horas e depois vai tomar por fim 24 horas. Ou seja, 24 horas, eu quero dizer meia-noite novamente. E esse remédio aqui de baixo, tu vai tomar ele 4 da manhã, depois vai tomar 8 da manhã, depois vai tomar meio-dia, depois vai tomar 16 horas, depois às
20 horas e depois às 24 horas de novo, vai tomar meia-noite. Ou seja, ah, 24 horas, né? Meia-noite é um múltiplo em comum. Sim, com certeza, né? Entendeu? A questão do caráter cíclico, isso aqui é um ciclo de remédios. O ciclo do medicamento A, ele tem uma frequência de três, ele tem um período de 3 horas e o ciclo do medicamento B tem um período de 4 horas. Perfeito. Agora vamos lá. Qual é o menor múltiplo comum? Qual é o próximo horário que você toma junto? Não é 24 horas. Por quê? Porque antes disso a
gente já viu aqui que existe o tempo meio-dia. Meio-dia tu vai tomar tanto remédio A quanto remédio B ao mesmo tempo. Então a resposta é essa. A resposta é essa. O próximo horário em que você vai tomar, próximo horário que você vai tomar os dois remédios juntos é meio-dia. Tomou meia-noite, agora vai tomar meio-dia. Tá bom? Detalhe, no momento que eu acho esse mmc, achei o mmc. O mmc, esse é meio-dia. Agora, se eu quiser saber todos os momentos em que tu vai tomar o remédio junto, é de 12 em 12 horas. Se eu já
achei, né, que depois que você tomou eles juntos, o menor múltiplo comum é 12. O primeiro momento em que você toma junto de novo é 12. Então agora é de 12 em 12. Não vai ter nada entre esses 12. Agora tu vai tomar o remédio junto às 12 horas, depois vai tomar meia-noite, depois 12 horas, depois meia-noite. Entendeu isso? Deu para compreender? Ótimo. Perfeito, né? Ah, isso é útil, né? Porque se ele falasse assim: "Ah, qual vai ser a sexta vez em que tu vai tomar o medicamento junto? em que tu vai tomar os dois
medicamentos, você faria assim: "Pere, tomou hoje meia-noite, aí vai tomar meio-dia, vai tomar meia-noite de novo, vai tomar meio-dia e vai tomar meia-noite de novo." Então, a primeira vez que você toma eles juntos, tirando essa daqui, né? É essa, a segunda, a terceira, a quarta, a quinta é meio-dia. Meio-dia de qual dia, né? Então aqui, ó, meio-dia de tá aqui no primeiro dia do segundo dia, meio-dia do terceiro dia, você toma ele junto de novo pela quinta vez. Deu para você entender isso? Tá beleza? Então, né? Tá tudo certo até aqui? OK. É, eu eu
quis dizer o seguinte, né? Tem gente perguntando isso. Ah, mas como assim de 12 em 12 horas? Eu quis dizer o seguinte: você entendeu como que eu cheguei no MMC? O mmc, o primeiro momento em que eles vão tomar esses medicamentos ao mesmo tempo é às 12 horas. Esse é o primeiro momento. Mas e agora? Para tu saber o próximo momento em que eles vão novamente tomar os remédios juntos? Agora, é só tu pegar esse MMC de 12 horas e você ir somando ele. Então, a cada 12 horas você descobre também isso, que a cada
12 horas você também toma os medicamentos juntos novamente, entendeu? Não vai ser algo no meio termo, não vai ser tipo, eles vão tomar juntos ali às 12 horas e agora vão tomar juntos às 4 horas. Não, não, não. Se o mmc é 12, então agora a cada 12 horas eles tomam juntos novamente. Beleza? Isso para qualquer número. Deu para você entender? A cada 12 horas eles tomam esse medicamento. Pedro, e se o na questão tivesse dito assim: "Olha, mas eu dei o medicamento quando era 1 da manhã." Mesma coisa. Você vai pegar o medicamento de
3 horas e de 4 horas, vai descobrir que o mmc é 12. A única coisa é o quê? Qual é o horário em que esse paciente vai tomar o medicamento juntinho? Às 13 horas. Só isso, só isso, entendeu? Pegou só isso às 13 horas, porque você já começou 1 da manhã. E aí me fizeram uma pergunta ali, falou assim: "Ah, mas nesse exemplo aí do quatro e do 7, isso não funcionaria?" Claro que funcionaria, você confundiu alguma coisa, entendeu? Porque funcionaria sim. Vou explicar como que funcionaria, tá bom? Ah, tem um medicamento que você vai
tomar a cada 4 horas e tem um outro medicamento que você vai tomar a cada 7 horas. Beleza? Comecei te dando esse medicamento à meia-noite e aí 4: da manhã você toma um deles, 7 da manhã você toma outro. Concorda? Aí o primeiro vai assim: "Ah, tomou 4 da manhã, tomou 8 da manhã, tomou 12 horas, tomou 16 e o segundo tomou 7 da manhã, tomou às 14 horas, tomou às 21 horas. Beleza? Qual o mmc entre eles?" É 28. A gente já tinha visto isso, lembra? É 28. Então, o que que quer dizer? Que
a próxima vez que tu vai tomar esses medicamentos juntos é às 28 horas. Mas, galera, é óbvio, o que que é 28 horas? Você vai ter que interpretar. 28 horas, quer dizer, vai passar um dia inteiro. Isso que é 28 horas. Você vai falar assim, não, vai passar um dia inteiro. Então, vamos lá. Aqui é meia-noite do dia o quê? Vamos colocar aqui do dia ã do dia 10 de janeiro de 2025. Quando que você vai tomar esses medicamentos juntamente novamente? O de o que você toma de quatro em quatro e o que você toma
de sete em sete após 28 horas, que é o mmc. É óbvio que tu vai ter tomado o medicamento, eh, que tem a o tempo de 4 horas, tu vai ter tomado ele 4 da manhã, 8 da manhã, meio-dia. 16. É óbvio. E o de sete em sete você vai ter tomado 7 da manhã, 14, tá? Mas eu quero saber quando que você toma junto. Junto de novo. É após 28 horas. Que que é 28 horas? Primeiro você avança mais 24 horas. Você vai agora para o mesmo horário, né? Meia-noite, porém do dia 11/01/2025. E
agora você ainda tem que botar mais 4 horas, né? Porque a gente tá falando de 28 horas. Então você vai tomar às 4 da manhã do dia 11, entendeu? 4 da manhã do dia 11, tá? Você tá no dia 11 agora e você vai tomar às 4 da manhã do dia 11. E aí agora para E quando que você vai tomar de novo? Esse que é o ponto. E quando você vai tomar junto de novo além desse dia aqui daqui a mais 28 horas. Aí você vai ter que pegar essas 4 da manhã, somar 24
horas para tu ir para 4 da manhã do dia 12 e somar mais 4 horas. E aí tu vai para 8 da manhã do dia 12. Deu para você entender? Deu para você compreender isso? Tá. Eu tô só formatando aqui a tela porque na gravação tá cortou uma partezinha aqui. Pronto, agora ficou legal. Deu para sacar? pegou, né? OK, então vamos nessa. Isso é mmc. Isso é mmc. Beleza? Isso aqui é mmc. Agora vamos lá. Qual é o método para você calcular o mmc? Então vamos lá. Ah, mmc aqui entre ajustando aqui minha tela de
novo. MMC que ero vou mostrar aqui com os mesmos números, né? Até pra gente ter uma facilidade. MMC entre o número 4 e 7. Eu listei todos os múltiplos e eu encontrei manualmente. Eu olhei e falei quais são, qual é ali o menor múltiplo comum. Mas é óbvio que isso aí é uma técnica que não é prática, porque quando você tiver números muito grandes, quando você tiver uma situação de prova, você não vai ficar listando todos os múltiplos para encontrar. Então eu vou mostrar aqui por partes assim. Vamos lá. Primeira técnica básica para você encontrar
o MMC. Essa técnica que eu vou mostrar é muito importante que você saiba ela e é muito importante que você aplique ela para você não esquecer, tá bom? Mas não é a coisa mais eh não é a coisa mais relevante de todas, não é a melhor técnica para fazer, tá bom? Eu vou até eu vou ter que mostrar com outros exemplos aqui, tá bom? Vou ter que mostrar o mmc, deixa eu pegar números aqui um pouco maiores, porque assim vai ficar melhor. MMC entre o número 12 e o número ã MMC entre o número 12,
o número 8ito, por exemplo. Vamos lá. Primeira coisa, você fatora todos os números. Eu quero saber o mmc entre o 12 e o 8. Primeira coisa é fator eles, tá? Então vamos faturar eles. O que que é faturar? você escrever o número em fatores primos. Então, como é que eu posso escrever o 12 como uma multiplicação de números primos? Cara, é simplesmente eu ir dividindo ele por números primos. Por exemplo, se eu dividir o 12 por 2, eu vou escrever que ele é 2 x 6. 12 por 2 dá 6, ou seja, 2 x 6.
Isso aqui ainda é o 12. Agora eu pego o 6 e eu vou quebrar o 6 em 2 x 3. Então aqui, ó, pronto. Concorda? O 12 tá escrito agora como um produto, ou seja, uma multiplicação de números primos. O dois é um número primo e o três é um número primo. Vocês lembram o que que é um número primo? Um número primo é um número que só pode ser dividido por pelo número um e por ele mesmo. O dois só pode ser dividido pelo um e por ele mesmo e o três também, tá bom?
Dando resto zero, é claro. Só que como é que eu faço para escrever um número na forma fatorada de números primos? Eu preciso agrupar as potências. Então, tá vendo? Esse 2 aqui é 2 x 2. Mas eu não escrevo assim 2 x 2, eu escrevo 2 elevado 2, tá bom? Vezes 3 elevado 1, porque o 3 só aparece uma vez. Então é simples. Esse aqui é o número 12. você vai ver que 2 elevado 2 dá 4 e vezes 3 dá 12. Quem não tiver entendendo de alguma forma, a gente já teve várias aulas sobre
isso, porque entrou bastante gente ultimamente na plataforma, né? Então assim, fiquem atentos, pois nós já tivemos várias aulas sobre isso. Elas estão lá no nosso cronograma de nivelamento. Basta que vocês assistam que vocês vão se interar perfeitamente da matéria, tá bom? E o número oito, como é que eu posso escrever ele? Ah, o número 8ito é 2 x 2 x 2. Detalhe, eu não posso escrever 2 x 4 porque o 4 não é primo. Por que 4 não é primo? Porque o quatro não é divisível só pelo 1 e pelo quatro. Ele também é divisível
pelo dois. Então ele não é primo, tá? Então eu escrevo como 2 x 2 x 2. Mas eu faço o quê? eu agrupo as potências, tá bom? Então aqui fica 2 elevado 3. Ok? Pronto, eu escrevi os dois. Agora o que que eu faço? Isso é muito importante. Eu vou multiplicar todos esses fatores uns pelos outros. Como assim? Todo mundo que apareceu vou multiplicar. Só tem um detalhe. Todo mundo que apareceu vai ser multiplicado um pelo outro. Mas os que apareceram ao mesmo tempo nos dois números, tipo dois, por exemplo, tá vendo aqui? O fator
do ele aparece tanto em cima quanto embaixo. Que que eu vou fazer? Eu vou escolher entre o que apareceu em cima ou embaixo o 2 elevado a 2 e o 2 elevado 3. Eu vou escolher aquele que tá com a maior potência. Com a maior potência, entendeu? Então dá uma olhada aqui. Agora eu tenho aqui 2 elevado 2 e tenho aqui 2 elevado 3. Quem eu vou escolher? Eu vou escolher o 2 elevado 3. Beleza? Então 2 elevado 3 vai ficar aqui. E aqui eu vou eu falei que eu vou multiplicar todo mundo um pelo
outro, tá? Aqui eu vou ter justamente o três. O três ele simplesmente vai ser multiplicado até porque ele não aparece aqui nos dois casos, tá bom? Então coloquei aqui apenas o três. Eh, ele tá aparecendo em apenas um caso volto. Agora, se tivesse aqui embaixo, se esse número aqui de baixo fosse feito de 3 elevado 3, o que que eu faria? Se ele fosse feito aqui embaixo de 3 elevado 3, eu escolheria o 3 elevado 3 e não usaria o 3 elevado 1. Deu para entender isso? Vocês conseguiram absorver? Eu vou multiplicar todo mundo que
apareceu. Mas quando eu tenho uma que aparece nos dois casos, tanto em cima quanto em baixo, 2 elevado 2 2 elevado 3, aí eu escolho a de baixo. Beleza? Pronto. Eu escolho, eu escolho a de baixo, não, eu escolho a que tem uma maior potência, né, que nesse caso é a de baixo. Eu vou dar mais exemplos aqui para isso ficar mais claro, tá bom? Agora vamos executar essa multiplicação. Quanto é 2 elevado a 3? É 8 x 3 é 24. Tá bom? Então 2 elevado 3 é 8, né? 2 x 2 x 2 é
o 2 vezes ele mesmo, 3 x 8 e xes 3 dá 24. Pronto. 24 é o mmc. 24 é o mmc. Deu para visualizar? Será que 24 é mesmo o mmc entre eles? Sim, com certeza, né? Você vai olhar aqui o número 12. Se eu for pegar os múltiplos do 12, quem são os múltiplos além do próprio 12? Logo em seguida vem o 24, depois vem o 36, depois vem o 48, depois vem o 60 e assim vai. Se eu for pegar aqui o oito, quem são os múltiplos do oito além do próprio oito, né?
Vai vir aqui o 16, depois vai vir aqui o 24, depois vai vir o 32, depois vai vir o 40 e assim vai. Ou seja, claramente aqui o 24 é o menor múltiplo que eles têm em comum. Deu para vocês sacarem isso? Vamos ver mais exemplos para vocês pegarem isso aqui melhor, né? Então, eh, vamos lá mostrar aqui. É que eu tenho que tô tô pensando aqui nos exemplos aqui. Eh, agora vamos pegar, podem pedir exemplos aí, quem quiser pedir no chat alguns exemplos, que eu vou resolver aí o que vocês pedirem, mas vamos pegar
aqui alguns números mais estranhos, né? Então, ah, eu quero saber qual é o mmc entre 7, entre 9 e ao mesmo tempo entre 12, tá? Olha só, aqui já é um caso eh não é tão simples assim de visualizar, porque eu quero um número que seja múltiplo em comum de todos esses caras, do 7, do 9, do 12 e eu quero saber qual é o menor deles, tá certo? Então vamos lá. Eh, detalhe, tá bom, galera? Sempre existe mmc, não existe um caso em que, ah, não tem mmc, sempre existe um mmc, eh, sempre existe
um menor múltiplo comum, tá bom? Sempre, sempre, sempre existe e um múltiplo em comum que é o menor deles, tá? Então não tem preocupação com isso. Depois já vou colocar aqui o outro exemplo que pediram ali, né? Entre 11 e 17. Beleza? Mas vamos lá. Vamos fazer isso aqui. Qual é o primeiro método que eu ensinei? O primeiro método que eu ensinei é você decompor cada número nos seus fatores primos. Então, como é que eu escrevo sete em fatores primos? 7 elevado a 1. O sete é isso. Ele é apenas o ele ele é um
número primo em si, tá? Como é que eu escrevo nove em fatores primos? O 9 é o 3 x 3. Lembrando que o trê é o número primo, então a gente pode escrever que na verdade ele é o 3 elevado 2, tá? É sempre importante agrupar as potências, tá? Qual é o mmc entre, qual é o número primo aqui? Como é que eu fator o número 12 em números primos? Tá? Eu vou escrever, por exemplo, pega o 12 e divide por qualquer número primo. Pode dividir pelo 2, ele vai virar o 2 x 6. Agora
tu pega o 6 aqui e tu transforma em 2 x 3. Tá bom? Então, na verdade, o 12 é quem? É o 2 elevado 2. Aqui já temos um 4 x 3. Aqui temos agora o próprio 12, tá bom? Que que eu faço agora? Eu multiplico todo mundo aqui. Eu multiplico todo mundo aqui, tá? Se tiver algum número que aparece ao mesmo tempo em mais de um, aí nesse caso eu vou escolher, se tiver um número que aparece ao mesmo tempo, mais de um, eu vou escolher o que tá com a maior potência. Beleza? Então
o 3 aqui, por exemplo, eu já sei que eu vou ter que escolher o 3 elevado a 2. Entre o 3 elevado a 1 aqui e o 3 elevado 2, eu vou escolher o 3 elevado 2. Agora vamos lá. Como é que eu pego o resultado disso aqui? Eu boto aqui o sete, porque o sete eu tenho que multiplicar todo mundo que tá aqui, né? Então vou multiplicar o sete. E agora vem um problema, tem aqui o 3 elevado 2 e o 3 elevado 1. Nesse caso, eu vou escolher o maior. Vou escolher o 3
elevado a 2. Beleza? E aqui eu tenho o 2 elevado a 2. Então vou vou colocar ele aqui também porque eu só tenho ele. Eu não tenho nenhuma escolha para fazer. Entendido? Agora vamos eh executar, né? 7 x 3 elevado 2, que é 9. x 2 elevado 2, que é 4. Então 7 x 9 dá 63. 63 x 4 a gente pode dobrar e dobrar, tá bom? Então isso dá 126, isso dá 252, ok? Então 7 x 9 63 x 4 dá o quê? 252, ok? Pronto, essa é a resposta. Esse aqui é o mmc
entre esses números, entre o 7, o 9 e o 12, ok? Agora esse é um método, tá? Esse é um método que não é o método que eu mais gosto. Esse não é o método que eu gosto de usar, tá bom? Não é mesmo o método que eu gosto de usar. Eu vou mostrar para vocês agora o método mais prático, tá bom? Antes de eu mostrar o método mais prático, eu vou eh fazer aqui só mais uma vez entre esses dois aqui, tá bom? Esses números aqui eles são números primos. Então, como é que eu
escrevo o número 11 e como uma como um fator de si mesmo? É, ele é o próprio 11. O 11 ele é um número primo, ele só pode ser escrito como o próprio 11. E o 17 aqui ele só pode ser escrito como o próprio 17. 17 é um número primo. O que quer dizer um número primo? Ele só pode ser dividido pelo um e por ele mesmo. Você consegue dividir 17 por 1? Sim, dá 17. E consegue dividir 17 por 17? Sim, dá 1. Não dá para dividir o 17 por nenhum outro número dando
exato. Você concorda comigo? Não dá. Então, nesse caso aqui, eu vou pegar o 11 x 17. E aí já fica aqui uma regra, né? O mmc entre dois números primos é sempre você multiplicar eles. MMC entre número primo, você multiplica um pelo outro. Beleza? Já fica agora essa regra aqui para vocês, tá bom? MMC número primo, você simplesmente multiplica eles e você encontra, tá bom? Então 11 x 17 vai dar ã 187. Beleza? Esse é o mmc entre eles. Ou seja, o que quer dizer isso? Que o menor múltiplo comum entre os dois é 187.
Se você pegar o 11, ah, eu vou te dar um medicamento de 11 em 11 horas. Quando que você vai tomar esse medicamento? Vai tomar ele às 11? Vai tomar 22? Vou colocando aqui só o tempo de horas, né? Vai tomar depois de 33 horas, vai tomar depois de 44 horas. Você vai ver que vai ter uma hora que você vai tomar depois de 187 horas. E se tu toma um medicamento a cada 17 horas, também vai ter uma hora que tu vai tomar depois de 187 horas. E aí que eles se encontram. Deu para
você entender? Deu para você sacar? Percebeu isso? Mas é o que eu tava dizendo. Esse não é o método, não é o método de mmc que eu mais aprecio. Qual é o método? E isso aqui tudo eu já tinha explicado em outra aula, né? Qual é o método de mmc que eu realmente aprecio? Tá bom? É você pegar todos os números, você traça um risco aqui. Agora esse isso aqui se chama divisões sucessivas por fatores primos, tá bom? Então você vai fazer agora divisões sucessivas por fatores primos. Como assim? Você coloca aqui do lado um
número primo e esse número primo vai dividir todo mundo aqui ao mesmo tempo, tá bom? E você sempre começa pelo menor número primo possível. Geralmente é o dois, o menor número primo possível, desde que um desses caras aqui, galera, pelo menos um desses caras precisa ser divisível por esse número primo que tu vai escolher. Então, por exemplo, ah, eu quero colocar o dois aqui. Ótimo. Mas pelo menos um desses caras é divisível pelo dois? Sim, o 12 é ótimo. Então agora tu vai colocar aqui os resultados de cada divisão pelo dois. Mas quando não for
possível fazer a divisão exata, você apenas repete o número. Por exemplo, quanto é 7 dividido por 2? Não dá para você fazer isso. Vai dar um número quebrado, vai dar 3,5, tá? Então você não vai fazer a divisão do 7 por 2, você vai apenas colocar aqui embaixo o quê? Ah, sete. Não fiz a divisão. E 9 divido por 2, mesma situação. Não dá para você dividir, tu coloca apenas o nove. E quanto é 12 dividido por 2? Aí dá para dividir, tu bota o seis. Agora eu te pergunto, qual é o próximo número primo
que pode entrar aqui para dividir pelo menos um desses caras que seja o menor número primo possível? É o dois de novo. Por quê? Porque o dois divide o seis aqui ainda. Então o sete não divide pelo dois, o ve não divide exatamente pelo dois e o seis divide dando três. Qual é o próximo número primo que eu posso colocar aqui que vai dividir pelo menos um desses caras e que seja o menor número primo possível? É o três, tá? O três é um número primo, só é divisível pelo um e por ele mesmo. E
ele divide esse cara aqui, tá? Então, por exemplo, o sete não é divisível pelo três, então você não faz nada, apenas repete. O 9 é divisível pelo três, inclusive a resposta é três. E o trê é divisível pelo três, a resposta é 1. Ó, isso aqui quer dizer que o número já foi decomposto. Se eu já cheguei aqui no 1, o 12 já foi decomposto, tá bom? O 12 ele já pode ser escrito com 2 x 2 x 3, ó. 2 x 2 4 x 3 12. Tá? Agora o 12 já morreu. Agora eu vou
continuar. Que número eu coloco aqui para dividir o 7 e o trê? Pelo menos um deles, né, para ser dividido é o próprio três, né? O três é um número primo, tem que ser sempre os menores números primos. E o três mata esse cara aqui. Ah, mas esse aqui não mata. Repete ele apenas. E o três virou um. Agora agora, quem é o número que eu posso colocar aqui? Número primo. Tá bom, Pedro? O cinco é o número primo. É, mas o cinco não divide nenhum desses caras. Tem que ser o quê? O sete. O
sete divide esse cara aqui. Pronto. Que que eu faço agora? Terminei, fiz a decomposição sucessiva em números primos. Eu multiplico todo mundo que tá ali na direita, todo mundo. Todo mundo. E eu vou achar o mmc. 2 x 2 4 x 3, 12 x 3, x 7, ã, dá 210 + 42, 252. Esse é o MMC 252, que é o que a gente tinha achado aqui pelo outro método. Mesma coisa. Entendeu? Sacou? Entendeu? Perfeito, né? Deu para entender? Então, a gente conseguiu aqui chegar. Esse é o método, tá? Esse aqui é o é o é
o método para você achar mmc. Ou seja, ou você pega cada número individualmente e escreve ele em forma de fatores primos, aglomerando as potências e depois você multiplica todo mundo um pelo outro. Porém, quando tiver um fator que foi repetido, por exemplo, o três foi repetido aqui e aqui, você vai escolher o da maior potência, tá? Sair aqui sem querer, você vai escolher o da maior potência, tá? Então eu escolhi aqui entre o 3 elevado 1 e o 3 elev 2. Escolhi o 3 elevado 2. Aí ficou 7 elevado 1 x 3 elevado 2 e
não 3 elevado 1 x 2 el 2. Ou eu faço e eu gosto mais de fazer assim sempre, tá bom? Eu mesmo sempre faço assim numa situação de prova. Eu boto os três números aqui e vou fazendo a decomposição por fatores primos. Beleza? Entendido, né? Tá. Agora vamos passar pra outra matéria. Vamos passar agora para MDC, tá bom? Então agora a gente vai explicar aqui MDC. Vamos lá então. MDC. MDC significa máximo divisor comum. Só um instante, antes de eu passar para essa aula, eu vou fechar a gravação dessa aqui para ficar a aula de
MMC completa. Então é isso. Aula de MMC tá. Sejam muito bem-vindos a mais uma aula da plataforma SAD. Agora a gente vai fazer aqui a nossa aula de MDC, tá bom? MDC é outra pegada, mas é bem parecido ainda, assim, tá bom? Os conceitos são muito parecidos, né? Eh, a gente tinha entendido agora mmc que é, eh, o mínimo múltiplo comum, tá? Então, a gente descobre ali qual é o menor número que é múltiplo daqueles dois ou daqueles três ou daqueles quatro que a gente tá avaliando, que seja comum eles, né, e seja o menor
possível. O MDC ele é o máximo divisor comum. Então, vamos fazer o mesmo estudo semântico, né, do que que significa isso, tá? Então, a gente tá falando aqui do máximo divisor comum, tá? Ou seja, eu quero pegar ali eh primeiro, né, dois ou três caras, claro, né, da mesma forma. Eh, se é comum, tem que ser sobre dois ou três caras, no mínimo. E eu quero saber um número que seja divisor deles dois, tá? O que que é um divisor? Um divisor é um número que consegue dividir aquele outro número sem deixar resto algum. Por
exemplo, eu tenho aqui o 30. Vamos pensar aqui quem são os divisores de 30, ou seja, quem são os números pelos quais eu posso dividir o 30 sem dar resto, tá? Primeira coisa, eu sempre posso dividir um número por ele mesmo. Sempre, né? Eu sempre posso dividir o 30 pelo próprio 30 e isso vai dar uma resposta que é um. Mas quem é o divisor nesse caso? Divisor é o 30, tá? E outra coisa, eu sempre posso dividir um número pelo um. Sempre dá para dividir qualquer número pelo um sem sobrar resto, tá? Então, os
divisores de um número, os divisores do 30, por exemplo, eles começam no próprio um. Eu posso pegar o 30, dividir pelo 1 e a resposta vai ser 30. Então, quem é o divisor aqui, ó? 30 dividido pelo 1, tá? Então, o divisor é o número um, tá? E a resposta disso vai ser 30, tá? E o resto vai ser zero. Beleza? Mas o divisor aqui é um. Então eu sempre posso dividir ele pelo um. E é claro que no final eu vou poder dividir ele pelo 30. O maior, os divisores de um número não são
infinitos, tá bom, galera? Não é que nem o múltiplo, que o múltiplo vai indo, vai crescendo. Agora o divisor não é infinito, tá? Os o maior divisor de um número é ele próprio, só dá para eu dividir o número no máximo por ele mesmo. Qual o maior divisor de 120? 120. E o menor divisor de 120 é um. Um número primo inclusive é aquele número que ele tem como divisor e só um e ele mesmo. E mais ninguém entre o caminho. Tá bom? Um rapaz falou assim para mim: "Ah, não entendi." Mas aí com certeza
absoluta você não viu as nossas aulas lá do ciclo de nivelamento, né? Porque você deve ter entrado bem recente na plataforma. Não tem problema, mas você precisa ir lá assistir, tá bom? Senão você vai ter dificuldade de acompanhar, tá? Então é, esse conceito de do que que são divisores, ele já foi trabalhado, né, na no ciclo de nivelamento, tá bom? Então, quero que você vá lá e você veja bem caprichado para você se manter num alto nível, ok? É, ele falou, ainda não vi, é isso mesmo, não tem problema, mas fica aqui na aula e
depois você vai lá ver. Então é isso. Vamos ver aqui quem são os divisores do 30. Ah, o por exemplo, ele é um divisor de 30, tá bom? O dois, o dois é um divisor de 30, com certeza dá para pegar 30 por 2 e a resposta vai dar 15, tá? O 3 é um divisor do 30. 30 di 3 dá uma resposta exata, dá 10, tá? O 4 é um divisor de 30. Não, não é 30/ por 4 daria 7,5. Isso não é um número um número inteiro, tá? Isso vai tá sobrando, vai tá
sobrando o resto, né? Na verdade 30 por 4 daria 7 com resto dois, né? Se eu pegar aqui 30 div por 4 vai dar 7 x 4 dá 28 e o resto é 2, tá? Ou eu poderia pegar esse dois e dividir quebrado pelo 4, que aí vai dar meio, aí vai ficar aqui 7,5, tá? Então, ã, o 4 não é um divisor do número 30, beleza? O 5 é um divisor do 30. O se aqui ele é também um divisor do 30. Ã, o 10 é um divisor do 30, o 15 é um divisor
do 30 e o 30 é um divisor do 30. Pronto. Esses aqui são os divisores do número 30. E só nenhum número mais é divisor do 30. Só dá para eu dividir o 30. Por quê? Perguntar se o 9 é. Não, 30 dividido por 9 não dá uma divisão exata, né? Você consegue dividir ali do do 30 pelo 9. Você só vai dividir o 27 pelo 9 que vai dar 3 e vai ficar faltando três para dividir pelo 9, tá bom? Então 30/ 9 daria 3,3. Tá bom? Então não é o 9, não é, tá
bom? vai sobrar um resto ali. Pronto. Esses aqui são os divisores do 30. Agora, e se eu pensar num outro número, pensa aqui agora num outro número que você vai colocar aqui. Pensa, por exemplo, no 40. Vamos analisar aqui quais são os divisores do 40, tá? Os divisores do 40, o 1, o 2, o 3, não é, não dá para dividir 40 por 3 e dá exato. Daria 13,3. Tá bom? Dá para dividir o 40 pelo 4 e dá exato. Dá para dividir pelo 5, 40 por 5 dá 8, certinho? Não dá para dividir pelo
6, pelo 7, dá para dividir pelo 8. Perfeito. Dá para dividir pelo 10. Perfeito. Dá para dividir o 40 certinho pelo 12? Não. Pelo 15, não. Pelo 20 dá. Dá para dividir o 40 pelo 20 e vai dar certinho. E dá para dividir pelo próprio 40 e vai dar certinho. 40 por 20 dá 2. 40 por 40. Esses que são os divisores do 40 e ponto. Ponto. Agora olha o que eu vou te falar. Olha que loucura o que eu vou te falar. Você vai entender agora de uma vez por todas. Eu tenho na minha
loja, eu sou marcineiro e eu tenho umas tábuas. Eu tenho aqui, ó, tábua e tenho aqui, ó, tábua de madeira, tá? Elas são bem parecidas, só tem uma única diferença entre essas tábuas de madeira. Você vai desbloquear agora a tua inteligência. Essa tábua aqui, ela tem 40 cm de e comprimento e essa aqui tem 30 cm. Só que eu não estão perguntando ali para mim, né? Mas para que que a gente usa o MDC na prática? Olha agora. Isso é um problema da vida real. Isso é um problema da vida real. Você tem tábuas de
40, tem várias tábuas de 40 na tua loja e tem várias tábuas de 30. Várias, tá? Não vou falar quantas aqui, depois a gente entra nisso. Ã, e só que eu tenho tenho o seguinte, eu vou te contratar para fazer um móvel e nesse móvel você só pode usar tábuas iguais, só tábuas de mesmo tamanho, entendeu? Só pode usar tábuas de mesmo tamanho, só tábuas idênticas. Beleza? Então, você não pode misturar tábua de 40 com tábua de 30. O que que você pode fazer? Por exemplo, você pode cortar essas tábuas, só que você tem que
cortar elas, tá? Você tem que cortar elas de forma que elas fiquem iguais. Então, por exemplo, Pedro, eu posso pegar essa tábua de 40 aqui e cortar ela em táazinhas de 1 cm? Responde para mim, pode ou não pode? Você, eu te pergunto, você vai conseguir pegar a tua tábua de 30 e também cortar em tábua de 1 cm? Vai, concorda? Vai ficar uma tabuinha pequenininha, entende? Essa tábua de 40 cm vai virar o quê? 40 tábuas de 1 cm. E essa aqui de 30 cm vai virar o quê? 30 tábuas de 1 cm. Mas
você vai conseguir trabalhar com tábuas idênticas. Todas as tábuas da minha fábrica tem 1 cm. Todas. Entende? Todo mundo entendeu isso? Que eu poderia pegar a cada tábua de 40 e cortar em tábua de 1 cm, 1 cm, 1 cm. Sim. Olha que pergunta interessante que estão me fazendo, né? Mas se a gente pensar um pouco, a gente tem a resposta. Olha que a menina perguntou assim: "Mas existe alguma forma de descobrir o mínimo divisor comum? Será que existe algum método?" Respondo aí. Existe algum método para eu descobrir o menor divisor comum entre o 30
e o 40? Ué, é sempre um. O menor divisor comum para qualquer número, quaisquer números, é sempre um. Tanto que eu fiz isso aqui. Eu falei assim, ó, vou dividir a tábua de 40 em quê? Pedaço de um. Eu usei um como divisor. Vou dividir a tábua de 30 em quê? Pedaço de um. Usei um. Deu certo? Deu. Entendeu? Pegou? É isso. O um é o menor divisor. O menor divisor em comum é o um. Agora eu vou te perguntar uma coisa. Você acha o Enem sempre cobra questões práticas? O Enem sempre cobra questão de
conceito prático. Você acha que se tu é o marcineiro, tu é o dono dessa fábrica, você quer pegar cada tábua tua de 40 e cada tábua tua de 30 e cortar tudo em tábua de 1 cm, você acha que você quer isso? Isso é uma coisa normal? É óbvio que não. Por exemplo, você não poderia ter pegado, invés de dividir essas tábuas aqui em tábua de 1 cm, você cortar tudo em tábua de 2 cm. Você não poderia ter feito isso? Cortar tudo em tábua de 2 cm. Claro que essa tábua de 40, ela geraria
o quê? 20 tábuas de 2 cm. E claro que a tábua de 30 geraria o quê? 15 tábuas de 2 cm. Então, em vez de você ter 40 tabuazinhas, você ia ter 20 tabuazinhas. Em vez de você ter 30 aqui, você ia ter 15 tabuazinhas de 2 cm e de 2 cm. Você concorda que já é melhor assim? Já é menos trabalhoso, né? Aí você fala: "Pô, Pedro, mas por que?" E você vai trabalhar com tábuas idênticas. Todas as minhas tábuas têm 2 cm, tá? Aí eu falo assim: "Pô, mas teria sido ainda mais fácil
se você tivesse escolhido fazer tábuas de 5 cm, porque essa tábua de 40 cm aqui, ela viraria oito tábuas de cinco. Oito tábuas de cinco, ó. Oito tábuas de 5 cm. E essa tábua de 30 viraria seis tábuas, 1 2 3 4 5 6 de 5 cm. Ó, seis tábuas de 5 cm. Perfeito. Estaria resolvido, né? Eu eu teria não precisar, imagina cortar tudo em 1 cm, depois cortar em 2 cm. Agora eu corto em 5 cm. Bem melhor assim, né? Eu vou ter, eu vou ter menos trabalho, não vou ter que ficar cortando, tá
bom? Aí você fala assim: "Pô, mas eu queria eu queria saber o seguinte. Eu já vi que eu poderia cortar em um, depois eu poderia cortar em dois, eu poderia cortar em cinco." Não tem como eu calcular logo qual é o maior tamanho possível dessas tábuas, mas que seja um tamanho que elas possam gerar pedaços iguais sem eu desperdiçar material. Aí você fala assim: "Vamos cortar em tábua de 20 cm. Vamos cortar em tábua de 20 cm, que aí as tábuas vão ficar bem grandes, né?" fala assim: "Ó, quero as maiores tábuas possíveis." Tá bom,
vamos lá. Vamos cortar em tábua de 20 cm. Olha que perfeito. Uma tábua de 40 eu só preciso fazer um corte e ela vira uma de 20 em cima de 20 em baixo. Até porque o 20 ele é um divisor de 40. É ou não é? O 20 é um divisor do 40. Então, ótimo. Eu vou fazer aqui duas tábuas de 20. O único problema é que quando e quando eu como é que eu vou pegar uma tábua de 30 e dividir em tábua de 20? Eu até consigo fazer, mas eu vou ter que jogar
10 fora desperdiço sem madeira. Porque que que eu vou fazer com uma tábua de 10? Eu preciso que todas as tábuas sejam iguais. Ou seja, o grande problema aqui é que o número 20 não é um divisor do 30, não é? O número 20 não é divisor do número 30. Ah, e se eu e o 15? O 15 é. Então vou pegar aqui o 30 e vou dividir em tábua de 15. Tábua de 15. Ah, mas aqui não vai funcionar. Aqui o 40 tu vai dividir em 15. 15 e vai sobrar 10. Qual é a
resposta para isso aqui? A resposta é o seguinte: eu preciso pegar essas tábuas e dividi-las. Preciso pegar essas tábuas aqui e dividi-las, transformar elas em um em uma tábua de um certo tamanho que seja o maior tamanho possível, mas que eu possa fazer com as duas tábuas ao mesmo tempo e não apenas com uma. Isso é o máximo divisor comum delas. Isso é o máximo divisor. Vamos voltar no número 30 e 40. Me diz o seguinte, que os divisores deles, olha só, o um não é um divisor em comum, claro que é. O dois não
é um divisor em comum, claro que é. O cinco não é um divisor comum, claro que é. Tanto que a gente dividiu em tábua de um, em tábua de dois, tá de cinco. O o 10 é um divisor comum. É. E olha só, o 10 é o máximo divisor comum. O 10 ele é o maior divisor comum que existe entre o número 30 e o número 40. Não tem outro divisor que seja comum e que seja maior. Ah, o 15 é um divisor, mas ele só é divisor do 30. O 20 é um divisor, mas
ele só é divisor do 40. Entendeu? É para isso que serve o máximo divisor comum. É quando você tem duas, três ou quatro estruturas, quatro quantidades, e você quer dividir elas, você quer agrupar elas em um certo conjunto, mas você quer que os conjuntos todos sejam iguais e você quer o maior possível. Você quer o maior conjunto possível. Então, nesse caso, eu tenho tábuas que tem 40 cm e 30. Eu quero usar só tábuas do mesmo tamanho, mas eu não quero ter que ficar cortando um monte de tábuas. Eu quero a maior tábua possível. Então,
quem é o máximo divisor comum entre o 30 e o 40? É o 10. Então, isso quer dizer o quê? que a melhor forma de eu fazer isso é cortar em tábua de 10, 10, 10. E aqui eu corto tábua de 10, tábua de 10, tábua de 10. Perfeito. Essa é a forma mais otimizada de cortar essas tábuas. Essa é a forma mais mais otimizada de todas de cortar essas tábas. E é aqui que a gente usa o máximo divisor comum. Deu para entender isso? Deu para sacar? Agora como que Vamos lá agora pra parte
prática, né? Como que eu calculo o máximo divisor comum? Como que eu faço para calcular esse máximo divisor comum, né? Tirando esse método que eu acabei de demonstrar, né, que é o método manual, que é você escrever todos os divisores e com base no que tu escreveu, você olhar e ver qual é o maior divisor que tá presente nos dois números, tá bom? Não, vamos ver aqui como que a gente calcula. Primeira coisa, você pode começar fatorando. Você pode começar fatorando da mesma falar assim, igual o mmc, eu posso começar pegando cada número e fator
sim, desde que você escreve em fatores primos, tá bom? Então, por exemplo, o como é que eu escrevo 30 em fatores primos? Cara, basta você dividir ele de qualquer forma e você agrupar em fatores primos. Como assim, Pedro? Sei lá, o 30 você não pode escrever como sendo 3 x 10? É, o três já é fator primo. O 10 é primo. Claro que não. O 10 não é divisível apenas pelo 1 e pelo 10. O 10 também é divisível, por exemplo, pelo 2, pelo 5. Então, eh, o 10 não é um número primo, mas agora
tu pega o 10 e escreve como número primo. Por exemplo, o 10 ele não pode ser escrito como 2 x 5. Pronto, 2 x 5. Tá tudo escrito em fator primo. Tudo. 3 é primo, 2 é primo e 5 é primo. Agora, quais são as potências? Só para deixar marcado, é um, tá? Então, esse aqui que eu escrevi, isso é o 30. Quanto é 3 x 2 x 5? 30. Agora vamos fazer o mesmo com 40. O 40 pode ser escrito como 4 x 10. Nem o 4 nem o 10 são primos. Mas se eu
pegar o 4 e escrever o 4 como sendo 2 x 2, aí isso é primo. E ao invés de 2 x 2, já vou colocar aqui 2 elevado 2, que aí já tá ali com a potência agrupada. E o 10 eu posso escrever como sendo 2 x 5, ó, 2 x 5, esse é o 10. Ah, só que eu vou pegar esse dois aqui e vou juntar aqui, tá bom? Então tenho 2 elevado 2 e aqui eu tenho 2 elevado a 1. Eu vou multiplicar essas potências, né? Eu vou ficar com 2 elevado 3. Se
eu tenho 2 elevado 2 x 2 elevado 1, na verdade mesmo eu tenho 2 elevado 3, tá? Vez 5. Pronto, tá resolvido. 2 elevado 3 é 2 x 2 4 x 2 8. E 8 x 5 é 40. Galera, tá travando alguma coisa? Uma menina falou que tá travando. Não, né? Tá, não é internet aí. Tá bom. Beleza. Fiz aqui a fatoração dos dois. Todo mundo acompanhou? Fiz a faturação. Fatorei os dois aqui. Que que eu faria para encontrar o mmc entre eles? Você lembra como é que eu encontrava o mmc, galera? MMC. Eu quero
o mínimo múltiplo comum. O mínimo múltiplo comum. Eu quero saber o seguinte. Quando eu for pegando, ó, múltiplos de 30, 30, 60, 90, 120, 150, 180. E quando eu for pegando múltiplos de 40, 40, 80, 120, eh, qual é o menor deles? Eu já sei só de eu falar aqui, né? Ó, pegando 30, ó, 30, 60, 90, 120. Agora 40, 40, 80, 120. Eu já sei que é o 120, o menor múltiplo comum deles dois, do 30 e do 40. Se eu quisesse achar por esse método, o que que eu faria? Multiplica todo mundo aqui.
Multiplica todo mundo. Mas quando tiver um cara que tá igual nos dois, eu escolho da maior potência. Então, vou multiplicar todo mundo. Por exemplo, tenho três aqui. 3 tá elevado a 1. Tanto faz aqui, né? 3 elevado 1 a 3. Ah, o dois apareceu aqui embaixo. Tem dois a um em cima e 2 a tr em baixo. Escolhe o maior. 2 a tr. Escolhe o maior. E o cinco apareceu em cima e embaixo. Nos dois casos, tá? 5 a 1. Tanto faz. Deixa 5 a 1 mesmo. Multiplica agora quanto é 3 x 8, né? Porque
2 a 3 é 8. Então 3 x 8 x 5. Vamos lá. 5 x 8 40. 40 x 3 120. Achei o mmc. Todos estão sólidos em mmc. Então, né? Acabei de repetir só o mmc. 120. É, o menor múltiplo comum é 120, certo? todos sólidos nisso, né? Maravilha. Mas eu não tô agora falando de mmc, eu tô falando de MDC. Pro MDC é o seguinte, eu vou também, já começa com o que tem de igual, eu vou também multiplicar a galera aqui. Eu vou também multiplicar a galera aqui, tá? Eu vou multiplicar quem tá
em cima, quem vou multiplicar todo mundo, mas não é bem assim, tá? Pro MDC, pro MDC não perguntaram, imaginei que a maior potência seria 2 elevado a 3, mas foi isso que eu fiz, não foi? Eu só escolho a maior potência quando tem repetição, entendeu? Para mmc, para mmc, lembra? Para mmc, eu vou multiplicar todo mundo que apareceu aqui. Só que quem se repetir em cima e embaixo, eu vou fazer uma escolha. Eu vou escolher quando tiver repetição, a maior potência, tá? O três não se repete em cima e embaixo. Eu boto o três. O
dois se repete em cima e embaixo. Escolhe agora. Tu vai escolher dois a um ou dois a três. Dois a três. O cinco se repete em cima e embaixo, mas só que eles estão com a mesma potência, então tanto faz. Então não tem o que escolher. Beleza? Sacou? Então isso aqui deu 120, que era o mmc. Pro MDC, prestem atenção, é diferente pro MDC, tá? Pro MDC a gente faz assim, primeira coisa, a gente só vai multiplicar os fatores primos aqui. Todo mundo aqui é primo, né? A gente só vai multiplicar os que dessa vez
a gente só multiplica quem apareceu em cima e embaixo. Já começa com essa regra. Você só bota na multiplicação quem tá em cima e embaixo. Por exemplo, o três apareceu em todo mundo em cima, embaixo. Não, o TR só apareceu aqui no 30. Então não interessa. Eu nem vou multiplicar o três. Percebeu? Eu não vou botar o três na minha multiplicação final para achar o MDC. Agora vamos lá. O dois apareceu em cima e embaixo. O dois apareceu. Apareceu tanto em cima quanto embaixo. Apareceu em cima 2 a 1 e embaixo 2 a3. Só que
nesse caso eu vou escolher a menor potência dele. Eu vou escolher a menor. Então, por exemplo, nesse caso aqui eu vou escolher a menor 2 a 1 e o cinco apareceu em cima e emembaixo. O cinco também apareceu. Apareceu como 5 a 1 em cima e 5 a 1 embaixo. Ou seja, tanto faz. É o 5 a 1 de dos dois jeitos. Quanto é 2 a 1 x 5 a 1? É 2 x 5 que dá 10. Porque o número elevado a um ele mesmo. Achei o MDC. Você lembra que o MDC era esse mesmo?
O MDC era 10 de fato. Sim ou não? Conseguiram pegar o primeiro método aqui de MDC. Galera, a gente vai fazer vários exercícios aqui, tá bom? Vocês vão ver isso com muito mais eh clareza, tá? Deu para entender? Ó, um, eu vou fazer aqui só uma coisa que o moleque falou assim, acabei de fazer essa questão aqui, formulei essa questão para você agora, para você resolver na aula, tá? Vamos lá. Deixa eu ler aqui a questão que o que que o menino fez. Ele falou assim, ó, só pra gente eh botar aqui na aula também,
né? Já que ele fez ali uma questão, deixa eu colocar aqui, tá? O engenheiro vai dividir dois trilhos de trem em sessões de igual comprimento para facilitar o transporte e a instalação. O primeiro trilho tem 840 m. Então, olha só, eu tenho um trilho de trem que tem 840 m, é imenso. E o outro trilho tem 1260 m também é imenso. O cara vai, vocês entenderam? O cara vai desmontar esse trilho todo e vai dividir o trilho para transportar, mas o cara quer dividir o trilho, o trilho sempre em pedaços iguais. Já entendeu? Você já
sabe que ele poderia pegar esse trilho de 840 m e dividir em quê? 840 pedaços de 1 m. poderia. Você já sabe que ele poderia pegar o trilho de 1260 m e dividir em 1260 pedaços de 1 m. Poderia, mas isso é o mais prático? Claro que não, pô. Tá dividindo muito pequeno. Divide logo num pedaço maior, né? Divide logo em pedaços maior. Por exemplo, lá, Pedro, ele poderia dividir em pedaços de 10 m. Concordam comigo? Sim ou não? Se eu tenho aqui trilhos que terminam com zero, eu posso dividir em pedaços de 10 m,
né? Então, 840 m dividido em pedacinhos de 10 m vai dar o quê? 84 pedaços de 10 m. E embaixo a mesma coisa, 126 pedaços. de 10 m. Olha só, todos os pedaços estão com 10 m. Você concorda? Mas aí eu te pergunto, será que esse é o melhor que eu posso fazer? Quem vai me dar essa resposta é o MDC. Eu quero saber qual é o máximo divisor em comum. Qual é o maior número pelo qual eu poderia dividir esses dois ao mesmo tempo. Eu já sei que eu posso dividir eles pelo um, já
sei que eu posso dividir pelo 10, mas, pô, eu queria saber o maior mesmo para eu poder não ficar cortando esse trilho em pedacinho de 1 m, 10 m. Eu queria cortar logo num pedaço que me ajudasse mais. Beleza? E aí continuando a questão, né? Ele quer que todos os pedaços do trilho tenham o maior comprimento possível, sem sobrar material. Tudo tá encaixado. Esse é o contexto mesmo que as questões dão. Qual deve ser o comprimento máximo então de cada pedaço? Tem que calcular o MDC entre esses dois números. Vamos calcular pelo método que eu
que eu tava ensinando agora, que é o método de você fator cada número. Depois eu ensino outro método, beleza? Então vamos lá. Vou fator cada número aqui. Vou escrever em fatores primos. Ah, o 840 eu já começo dizendo que ele é 84 x 10. Nenhum desses dois aqui é primo, óbvio, né? Mas se eu pegar o 10 aqui e escrever o 10 como sendo, deixa eu até inverter a ordem, tá bom? Eu vou colocar aqui ele é 10 x 84. E eu já vou escrever agora que o 10, na verdade ele é 2 x 5,
tá? Vezes 84. Pedro 84 não é primo, tá? Divide ele pelo que tu quiser. Pedro, posso dividir o 84 por 2, vai dar 42. Eu vou escrever que 84 é 42 x 2. Tá bom? Tá ótimo. Então 84 é 2 x 42. 42 não é primo. P. Então escreve 2 x 21. Porque o 42 é isso, né? Duas vezes o número 21. duas vezes o número 21. O 21 não é primo. O 21 tu pode escrever como 3 x 7. Só tô vendo o número primo aqui agora. 2 5 3 7. Agora eu agrupo, né?
Só para deixar isso certo. Então 2 2 2 2. Eu tenho três números dois. Eu vou escrever que isso aqui é 2 a tr. Beleza? Isso aqui na verdade é 2 a tr. 2 elevado 3. Eu tenho um número 5, beleza? Eu tenho um número 3. Então aqui, ó, 2 elevado 3 x 3 x 5 x 7. Galera, eu agrupei aqui. Isso aqui é o 840. Beleza? Quer testar? Quanto é 2 elevado 3? 8. 8 x 3 8. Vamos fazer primeiro. 8 x 5 40 x 3= 120. 7 x 120 x 100 700. 7 x
20 140, 840. Você viu que não é difícil, né? Não é difícil. Concorda? Fator não é difícil. Então, legal. Já tenho aqui meu primeiro número assim. Agora, e o 1260? Cara, começa escrevendo 10 x 126, né? Porque 1260/ 10 dá 126. Então, 126 x 10, que ó, 10 x 126 é o 1260. Mas o 10, né? Você já vai trocar por 2 x 5.6. Isso é o 1260. O 126, Pedro, posso dividir por 2, vai dar 63 e escrever que é 2 x 63. Pode. E se eu invés de fazer isso, quiser dividir por três,
que aí vai dar, né, 42? Aí eu eu vou escrever que o 126, na verdade, ele deu 3 x o 42. Ótimo. 126 você escreve que é 3 x 42. Pedro, mas eu quero botar que o 42 ele é 6 x 7, porque eu lembro que a tabuada é essa. Tá ótimo. 42 é 6 x 7. Mas eu quero dizer que o seis, o se não é primo, eu quero dizer que o se na verdade ele é 3 x 2. O 6 é 3 x 2. 2 x 3. Perfeito, tá tudo primo aqui. Agora vamos
agrupar isso aqui. Tem número dois aqui e número dois aqui. Então na verdade eu tenho 2 elevado 2. Já apaga esse dois aqui. Eu tenho aqui número três e número três. Então na verdade eu tenho também 3 elevado 2. E eu tenho aqui número 7. Tá tudo escrito em número primo. Quer testar? 2 el 2 4 x 5 20. 20 x 9, né? Que é o 3 elevado 2 dá 180. 7 x 180, a mesma coisa que 7 x 200 - 140. 100 - 140 1260 já era, tá tudo fatorado. Como que eu procedo para
encontrar o mmc? Eu, ele não perguntou isso. Pelo amor de Deus. O mmc é são eh, eu vou pegar o mmc, por exemplo, tem 840. Eu vou ter o múltiplo de 840, que é 1680. Eu quero saber qual é o múltiplo que vai tá, qual é o menor múltiplo tanto 840 quanto 1260. Vai ser um número gigante. Só para lembrar, né? Se eu fosse fazer o mmc, eu ia ter que multiplicar todo mundo que aparece aqui. Porém, quando tivesse aparecendo ao mesmo tempo, em cima e embaixo, eu precisaria fazer uma escolha. Beleza? Então aqui tá
aparecendo dois em cima e embaixo. Eu vou escolher o 2 a trê ou 2 a do? Eu vou escolher o dois a tr porque eu quero mmc. Eu escolho pro mmc sempre o número, a maior potência. Beleza? Ã, o três tá aparecendo em cima e embaixo. Eu vou escolher a maior potência. Vou escolher a de baixo que é o 3 elevado a 2. Mnc. Nem é o que a questão pediu, galera. A questão pediu para eu cortar isso aqui. Então pra questão eu quero mdc. Beleza? Vamos lá. Ã, e o cinco aparece em cima e
embaixo, mas ele é o 5 a um mesmo, tanto em cima quanto em baixo. E o sete mesma coisa. Quem é o mmc? O mmc é 8, que é o 2 a 3, x, que é o 3 a2 x 5 x 7, tá bom? 8 x 5, 40. 40 x ã 40 x 7 dá 280. E agora 280 x 9 foi o que sobrou, né? Dá 2800 - 280, 2520. 2520 é o MC entre esses dois números. Mas ele não pediu isso. Eu só tô revisando com vocês. Agora você vai ver que é mesmo, né?
Você vai ver que é mesmo. Por exemplo, 840. Vamos pegar os múltiplos de 840. Tem 1680. Agora eu vou botar mais 840. Vai dar 2400. 2520. Agora vamos pegar os múltiplos de 1260. O próximo múltiplo de 1260 já é também o 2520. Ou seja, o mmc é mesmo 2520. Legal. Tá. Mas ele não pediu nada disso. Ele pediu para eu pegar trilhos de trem que tem e um trilho é grandão, 840 m, outro tem 1260 m. Ele quer cortar isso aqui em tamanhos de tábua semelhantes, tá? Para isso, eu quero o MDC. Só que o
início do processo é parecido. O início do processo eu faço a fatoração e reúno as potências. Agora o que que eu faço depois é que muda, né? O que que eu faço agora? O que que eu faço agora para achar o MDC? Eu não vou sair multiplicando todo mundo, nada disso. Primeira coisa, só entra na minha multiplicação o quê? Vocês lembram quem apareceu tanto em cima quanto em baixo. Já começa por aí. O dois, por exemplo, apareceu em cima e embaixo, apareceu, ele vai entrar. O três apareceu em cima e emembaixo, apareceu, ele vai entrar.
O cinco apareceu em cima e baixo, apareceu. O sete apareceu. É, nesse caso aqui todos vão entrar. Só que além de ter que aparecer em cima e embaixo, eu preciso da menor potência e não da maior, tá? Você pode gravar que é o inverso, né? Quando você tá calculando mínimo múltiplo comum, você procura as maiores potências quando tem repetição. E ao contrário, né? Mínimo múltiplo, você calcula as maiores. E quando você tá procurando o máximo divisor comum, você usa as menores potências. É o inverso do que parece, você pode lembrar assim, tá? Vamos lá. Ã,
mas também isso aqui você sempre pode confirmar na hora da prova, né? Você sempre pode verificar, pegar, escrever os múltiplos ou os divisores e ver se faz sentido o que você achou. Então não tem muito o que confundir aqui, mas vamos lá, tá? Só vou multiplicar quem apareceu em cima e emembaixo. O dois apareceu, mas eu quero a menor potência. Então eu quero essa daqui, tá? O três apareceu em cima e embaixo, mas aqui ele aparece como 3 a 1 e aqui 3 a 2. Eu vou escolher quem? Eu vou escolher o 3 a 1.
O cinco aparece em cima e emembaixo. Ele aparece igual, galera. Então tanto faz. Eu vou escolher. Tanto faz. Cinco. Não é a mesma coisa que tá em cima e embaixo, tá? E o sete também aparece em cima e embaixo. Tanto faz. Eu vou escolher sete, mas é a mesma coisa, tá? Agora multiplica 2 elevado 2 x 3 x 5 x 7, tá? 2 elevado 2 dá o quê? 4 4 x 3 x 5 x 7 4 x 5 20 Eu sempre procuro já fazer isso porque 20 é fácil, né, de multiplicar. Eu sempre gosto já
de pegar logo ele. Então 4 x 5 20. 20 x 3 60. 60 x 7, né? Dá 420 porque ã 7 x 6 42, né? Então achei o mdc. Olha que maravilha isso aqui. A perguntaram por que que você não pegou 2 elevado a três. Ele não é maior. Mas eu falei que para m descer o oposto. Você você viu que tá moscando. Eu falei agora várias vezes. Falei para M desc oposto. Você pega o menor, pega o menor. Pô, por que que eu não peguei o 2 elevado a 3? Porque a regra é pegar
o menor, entendeu? Acabei de falar isso. Tudo não tem problema, faz parte, né? Mas isso é para vocês verem como que é importante assistir as aulas mais de uma vez. Porque tem, vocês precisam entender o seguinte, tá bom? Deixa eu contar uma coisa para vocês. Escuta o que eu vou falar agora. Não levem como ofensivo, tá bom? Porque eu vou me incluir isso nisso, tá bom? Não levem como ofensivo, mas nós somos a geração intelectualmente mais sequelada e ferrada da história da humanidade. Vocês sabem disso? Vocês têm ciência disso? De que vocês são praticamente débes
mentais? E eu também sou. Vocês sabiam que todos nós somos doentes psiquiátricos? Tô falando sério. Todos nós somos doentes psiquiátricos. Todos nós somos expostos a um nível de estímulo, a um nível de bombardeamento, de formação. Eu tô me incluindo nisso. Absurdo que deixa a gente débental. Então, se você não perceber que você é praticamente um débo mental, que o teu teu tempo de prestar atenção numa coisa é ridiculamente pequeno, que você vive na era da maior desatenção possível, você vive na era do transtorno mental em que todo mundo tem depressão, ansiedade e comportamentos anormais. Todo
mundo, não é uma ofensa, não. Você tem que agir de acordo com isso. Você tem que falar assim: "Eu preciso recuperar a minha inteligência. Eu preciso assistir as coisas várias vezes. Eu preciso estar cada vez mais focado. Senão você vai vir aqui, vai assistir a aula. Ah, não entendi. Ué, é porque durante a aula mesmo, toda hora você tá parando. Toda hora Então é só. Você viu um exemplo? Eu tava falando agora, agora, agora uma coisa aí o moleque acabou de perguntar isso porque o cérebro dele não aguenta prestar atenção aula, isso não é uma
ofensa, para você sequência, isso tem cura. Mas para isso ter cura, você precisa se acostumar a estudar de verdade por por longos períodos de tempo, tá bom? Senão você nunca vai ser aprovado em medicina. Isso já é fato, tá? Vamos lá. Então, isso eu me incluí nisso para vocês terem que eu também me incluo nisso, tá? Então vamos lá. 420. O que que quer dizer? Que a melhor forma de eu pegar e um trilho de 840 e um de 1260 e dividir eles em pedaços iguais é dividindo pelo 420. Então, tá vendo aqui o trilho
de 840? Esse trilho vai gerar um pedaço de 420 e outro pedaço de 420. Tá vendo o trilho de 1260? Ele vai gerar um de 420, outro de 420 e outro de 420. Pronto. Eu consigo transportar em pedaços idênticos de 420 m. Entendeu? Perguntaram por que que não pode ser 210? Ué, também pode. Claro que pode ser. Você pode, se tu quiser pegar esse trilho de 840, em vez de dividir em dois trilhos de 420, você dividir em quatro trilhos de 210. Mas ele não tinha pedido, ele não tinha dito que ele queria que os
pedaços fossem os maiores possíveis. Lembra que a gente tá olhando o máximo divisor comum? O 210, ele é de fato um divisor comum para todo todos aqui. Concordo contigo? Tudo todo mundo aqui pode ser dividido nesses pedaços de 210, né? Todo mundo pode ser dividido em pedaços de 105, mas não é o maior de todos. O maior de todos é 420. Se ele colocasse na questão algum algum requisito, às vezes ele coloca: "Eu quero os maiores pedaços de todos, mas não pode passar de 4 m." Aí você fala: "Tá, o MDC é 420, né? Não
pode passar de 400 m, mas não vou poder usar o MDC, vou ter que usar o próximo menor, que é o 210. Vai ter questão que a gente vai usar isso, tá bom? Esse é o método aí de obtenção do MDC, só que assim como eh no outro caso, né, de mmc, tá? Assim como no caso do do mmc, não é o meu método favorito, tá? Existe um outro método que é o seguinte, você pega os números, vou até usar o mesmo exemplo, tá bom? Você coloca lado a lado, mesma coisa, tá? Mesma coisa. Escuta
só essa daqui. Você pega os números, você coloca lado a lado e você vai fazer o quê? Vai dividir por números primos, pá, pá, pá. Lembra disso? A única diferença é que quando você quiser o MDC, você só vai colocar um número aqui, um número primo aqui, se se ele for capaz de dividir todo mundo que tá aqui. No mmc não era assim. No mmc a gente colocava aqui o dois, só que o dois não não precisava ser capaz de dividir todos os que estão aqui. O dois aqui não conseguia dividir o sete, não conseguia
dividir o nove, mas ele dividia o 12. Então dane-se já é o suficiente, tá? Agora, no caso do MDC, se você não quiser fazer assim, olha, eu vou fator os números e vou multiplicar quem aparece em cima e embaixo e vou escolher quando aparecer em cima e emb baixo. Não, eu só vou multiplicar quem aparece, mas sempre escolhendo as menores potências. Se você não quiser fazer assim, você vai fazer desse jeito aqui. Vamos lá. Números primos pra gente colocar aqui. O dois, por exemplo, a regra para achar o MDC é que ele tem que dividir
todo mundo aqui. O dois divide todo mundo, divide, porque os dois são pares aqui, né? Esse é o critério de divisibilidade. Então, eu posso sim colocar o dois aqui. Vamos lá. Resultado da divisão 420 aqui. E aqui o resultado da divisão é 630. Vamos lá. E o dois aqui agora, quer dizer, per quem é o próximo número primo aqui? Eh, do menor pro maior, né? Que divide todos. É o dois de novo. O dois divide eles dois aqui, tá? Ã, então eu coloco detalhe, tá bom? Eu vou explicar para vocês. Tem macete depois, né? Você
poderia já começar dividindo pelo dois e pelo cinco, que é como se fosse o 10 e cortar aqui, mas eu vou mostrar aqui o método tradicionalzão, tá? Então aqui vou dividir por dois de novo. Deu 210 aqui e aqui deu 315. Vou colocar o dois aqui de novo, porque dá para dividir 210 pelo 2. Concorda? 210 é par divisível pelo 2. Não, não vou colocar. Não posso colocar o dois aqui porque só podem entrar aqui números que vão dividir todo mundo aqui e o dois não divide o 315, por exemplo. Então não é permitido que
eu coloque o dois. Se eu quero achar o MDC, claro, se eu quero achar o MDC, eu não posso colocar o dois aqui. Posso colocar o três, depende. O três divide todo mundo, divide 210, né? Para saber se o número é divisível por três, a gente soma os algaritmos dele. 2 + 1 dá 13 é divisível por 3. Divide o 315. Vai soma 3 + 1, 4 + 5, 9. 9 é divisível por 3. Isso tudo tá nas outras aulas da plataforma para quem chegou agora e não tá entendendo, tá bom? Vai lá em cronograma
de nivelamento e assiste, tá? O três então funciona porque os dois são divisíveis pelo três. Executa agora. Executa, tá? Então aqui vai dar 70 e aqui vai dar quem? 315/ 3. Se fosse 300 daria 100 e 15 dá 5. Então dá 105. Quem eu coloco aqui agora? Tem que sempre ir crescendo, não posso voltar no dois nunca, né? Agora eu vou tentar colocar o três de novo. Vou tentar colocar sempre o menor número primo possível. O três pode funcionar aqui? Ah, o 105 é divisível pelo 3, né? Porque o mais 5 é 6. Mas o
70 não é, cara. O 70 não é divisível pelo 3, certinho. Então esquece três. Não pode botar o três aqui de forma alguma. Então pensa no próximo número primo. Cinco. Será que pode colocar cinco? Depende. O 70 é divisível pelo 5. Qualquer número que termina em zero ou cinco é divisível por 5. Então 70 é. E o 105 termina em zero ou 5 é também. Então 5 vale 70/ 5. Mcete mental, né? Para dividir macete mental para dividir o o número por cinco, você dobra e divide por 10, né? Então 70 vira 140, 14. 105
di por 5 vira 210, 21, né? Dobra e divide por 10, tá? E agora o que que eu faço aqui? Tá e boto 5 de novo. Ã, não, porque o 5 não, nenhum dos dois é divisível pelo 5. Boto o 7, é um número primo. É o 7, os dois funcionam. Então, 14/ 7 dá 2 e o 21 div pelo 7 dá 3. E agora existe algum outro número que eu possa colocar aqui que vai fazer os dois serem divididos ao mesmo tempo? Não, não tem. Acabou. O MDC vai vir de você multiplicar isso aqui
tudo. Acabou. 2 x 2= 4. 4 x 3= 12. 12 x 5 60 x 7. E eu gosto assim. Eu prefiro fazer assim. pegou, entendeu? Sacou? Tem gente falando: "Ah, eu faço igual a MMC, mas circulo somente os números que dividem". É, é a mesma coisa desse método, mas assim é um algoritmo mais confiável. Você só bota aqui o que realmente é, tem gente que bota os dois, né? Eu sei, bota uma tabela só pro 840, bota uma só pro 1260, aí circula. É, eu não gosto. Eu só ensino dessas duas formas, das três formas,
né? Então, ou você escreve os divisores e encontra manualmente, tá? ou você eh você eh fatora os números e escolhe os que aparecem em cima e embaixo e multiplica as menores potências. Ou você coloca eles numa tabela e só escreve números que consigam dividir, números primos que consigam dividir todo mundo ao mesmo tempo e multiplica esses números, tá? Eu gosto de fazer dessa forma. Lembrando que se eu quisesse o mmc, eu não faria isso. Se eu quisesse o mmc, aí eu colocaria aqui, eu ia colocando os menores números primos, independente se eles dividem os dois.
Então o dois aqui, tudo bem? Divide os dois, 420 aqui, dá 630. Aí boto o dois de novo, ele divide os dois aqui, beleza? 210 e aqui dá 315. Agora eu boto o 2. Ah, mas o dois não divide o 315. Não interessa. O dois divide pelo menos um, eu vou colocar mmc. Mmc, tá? Então vai dividir aqui por 105. E aqui não acontece nada. Agora dá para botar o dois? Não dá. Dá para botar o trê? Dá. Então o três vai dividir aqui por isso aqui vai dar 35, né? Dividindo por três. E isso
aqui vai dar 105. Aqui agora entra o três de novo. Entra por causa desse aqui. Ah, mas o três não divide esse cara. Mas mmc não precisa dividir todo mundo, tem que dividir pelo menos um. Então aqui vai dar agora 35 e aqui vai dar 35. O cinco funciona? Funciona. O cinco vai fazer isso aqui gerar 7, gerar 7. Agora boto o sete aqui. Gerou um. Gerou um. MMC eu multiplico todo mundo que tá aqui. 2 x 2 x 2= 8. 8 x 9 72. 72 x 5 360. 360 x 7 2100 + 420. Que
é o mmc que a gente tinha achado anteriormente também. Para MDC eu só boto aqui na coluna da direita os números que naquele momento consigam dividir todo mundo que tá na esquerda simultaneamente. Depois eu multiplico. Eu gosto muito assim. Eu ensino dessa forma. Vocês veem que tem várias formas de fazer isso, mas as vocês observaram, olha, olha que que legal isso, né? Eu tô falando sério, tem várias formas de fazer isso, né? Tem professor que acha que tá ajudando quando começa a ensinar várias formas. Ah, você bota uma tabela aqui, você circula isso aqui, tá?
Mas eu ensinei de um jeito sistemático. Por exemplo, eu falei para MMC e MDC existe o primeiro jeito, né? Que é você listar todos os múltiplos ou todos os divisores dos números e circular os que são ali os maiores ou os menores. É igual pros dois, só muda o que você vai procurar. Depois eu listei o quê? você pode fator o número. Aí eu falei, mas pro mmc você multiplica todo mundo aqui e aí os que se repetirem você escolhe o da maior potência. E pro MDC você multiplica só os que aparecem em cima e
embaixo e escolhe o da menor potência. Aí eu falei pro mmc você pode colocar os números aqui numa tabela e faturar eles. A única diferença é que pro mmc você coloca você eh coloca os números primos lá, mesmo que eles só dividam um cara e multiplica todo mundo no final. E no MDC você só coloca os números que dividem todo mundo e multiplica todo mundo. Ou seja, vocês entenderam os três métodos que eu ensinei, eu ensinei pro MMC e pro MDC de maneira estruturada e didática e mostrando exatamente qual a diferença entre cada método. Por
isso que funciona assim, é assim fica na tua cabeça, tá? Assim que fica de verdade na tua cabeça. Vocês têm que ter visto também o cronograma de nivelamento, tá bom? Então agora vou encerrar aqui a aula de MDC e na próxima aula aqui os exercícios que eu separei para hoje, beleza? Parabéns a todos que assistiram e vamos para Sejam todos bem-vindos a mais uma aula da plataforma SAD. Agora a gente vai resolver exercícios aqui tanto de mmc quanto de MDC, tá bom? Simultaneamente, no caso, eu não vou dizer a princípio qual exercício é de que,
né? A gente tem que descobrir isso, tá? Então vamos lá, começando aqui. Ã, primeiro exercício aqui, coloquei aqui numa ordem meio que aleatória, coloquei alguns exercícios do Enem, alguns não são, tá? Vamos lá. Ã, o gerente de um cinema fornece anualmente ã ingressos para ingressos gratuitos para escolas, tá? O cara é gerente, então você sempre tem, sabe disso, né? Tem que sempre ler imaginando, tem que sempre ler, processando ali mentalmente o que você tá vendo, tá? Então tem que imaginar, pô, o gerente do cinema, ele vai dar ingressos para escolas, tá? E aí, que que
tem? Ã, este ano serão distribuídos 400 ingressos para uma sessão vespertina, né? Ou seja, uma sessão de tarde e 320 ingressos para uma sessão noturna de um mesmo filme. Então, o cara tem aí um número total de ingressos. Eu tenho 400 ingressos para uma sessão da tarde e 320 ingressos para uma sessão da noite. Várias escolas podem ser escolhidas para receberem ingressos, várias, tá? Alguns critérios paraa distribuição dos ingressos. Então, olha isso aqui, ó. Cada escola deverá receber ingressos para uma única sessão. Então, já começa por aí, tá? Só para vocês entenderem o que que
significa pegar esses ingressos e distribuir esses ingressos para escolas. Vocês têm noção disso? O que que significa distribuir? Quer dizer, justamente dividir esses ingressos para várias escolas, né? Se eu pegar aqui 400 ingressos e eu vou dividir esses ingressos para 10 escolas, eu tô dizendo que cada escola vai receber 40 ingressos, tá? Se eu pegar e esses 400 ingressos e falar assim: "Ah, eu vou dividir em grupos de 40 ingressos, grupinhos de 40 ingressos". Também posso pensar assim, 400 ingressos que eu vou dar de 40 em 40, eu vou contemplar 10 escolas com isso. Beleza?
Legal. Ã, vamos ver agora quais são as regras, né? Cada escola deverá receber ingresso para uma única sessão. Ou já quer dizer o que? Que eu não posso misturar, eu não posso pegar eh dar ã não posso, por exemplo, né? Ah, vou distribuir aqui 100 ingressos para cada escola. Aí aqui eu tenho os 400 ingressos de uma sessão e os 320. Eu falo assim, vou dar 100 ingressos para cada escola. Aí eu vou pegar esses 400 aqui e vou dividir aqui em grupo de 100. Grupo de 100 para uma escola, grupo de 100 para outra
escola, grupo de 100 para outra escola. E aí esses 320 aqui eu divido em grupo de de 100, em grupo de 100. Não, não, não era nem isso que eu ia mostrar, não é esse exemplo aqui não. Eu não posso pegar assim e falar: "Vou dividir isso aqui em grupo [Música] de aqui. Boa, vou dividir em grupo de 60 ingressos". Eu não posso fazer isso, ó. Ah, vou dividir em grupo de 60 ingressos. 60 ingressos para cada escola. Então aqui, ó, 400 eu vou dividindo. Ã, quando eu chegar ali em seis escolas contempladas, eu tenho
360 ingressos. Aí agora eu só tenho mais 40, né? Aí eu falo assim: "Não, não tem problema, porque esses últimos 60 aqui, eu vou pegar esses 60 fazendo 40 do desses 400 que sobraram e 20 desses aqui." Aí eu dei 60 ingressos pra escola. Agora só sobraram 300 desse aqui. E esses 300 eu divido também em grupo de 60 certinho, ó? Dividir todos os ingressos. Então, mas as escolas têm que receber sempre o mesmo ingresso. Então, quando você fez isso aqui, você misturou ingresso de duas sessões. Então, você também violou já o primeiro conceito, tá?
Tô só dando uma demonstração, né, do que do que que significa cada critério na prática. Hã, todas as escolas deverão receber o mesmo número de ingressos. Eu já tava usando isso agora, né? Eu tava já fazendo com esse critério de que toda escola tem que receber o mesmo número de ingressos, tá? Então, eh, não pode uma escola receber 60 e outra escola receber 30, 20. Todas as escolas têm que receber o mesmo número. Ou seja, já dá para saber que tem que ser um número. Eh, quero só que vocês entendam, só desse aqui a gente
já consegue ter noção, né, de que só desses dois critérios já dá para ver que tem que ser eh tem que pegar esse ingresso, né, tanto os 400 quanto os 320 e dividir em pacotes, tá? de modo que cada escola receba o mesmo número de ingressos e sempre pra mesma sessão. Então, por exemplo, posso pegar tanto os 400 ingressos aqui quanto os 320 ingressos e dividir eles em grupos de 10? Posso, né? Vou pegar aqui os 400 e vou dividir em grupo de 10. Então, quantas escolas vão ser contempladas? 40 escolas, né? 400 ingressos divididos
de 10 em 10, 40 escolas contempladas, tá bom? Então, aqui eu vou ter 40 escolas contempladas com 10 ingressos. São 400 ingressos. E aqui eu também vou dividir, não mesmo número. Cada escola tem que receber o mesmo número de ingresso. Então cada escola tem que receber 10 ingressos. Ótimo. Então 320/ 10 vão ser o quê? 32 escolas recebendo 10 ingressos cada uma. Tá tudo certo. Tudo certo, Pedro. Cada escola recebeu 10 ingressos. Eu tenho 40 escolas contempladas e mais 32 escolas. Eu tenho 72 escolas contempladas, todas recebendo o mesmo número de ingresso e cada escola
recebeu um ingresso somente por uma sessão. O meu raciocínio que eu falei aqui, respondam agora mentalmente aí na casa de vocês, está certo ou não tá? Tá certo. Totalmente certo. Você precisa ter essa clareza. É totalmente legítimo pegar os 400 ingressos, 320 e dividir tudo em pacote de 10 ingressos. E eu vou ter 72 escolas contempladas, cada uma com 10 ingressos. Ótimo. Beleza. Não haverá sobra de ingresso, tem que distribuir tudo. Perfeito. Também está tudo certo. Agora vem o único problema. Olha a pergunta. O número mínimo de escolas que podem ser escolhidas para obter ingressos,
seguindo critérios estabelecidos. É, e aí quando ele fala o número mínimo de escolas que podem ser escolhidas para obter ingressos, quando ele diz o número mínimo, por exemplo, na minha conta aqui são 72 escolas contempladas. Para eu obter o número mínimo de escolas, eu preciso dar o máximo de ingressos para cada escola. O máximo de ingressos para cada escola. Você entende? Eu preciso fazer assim, dando 10 ingressos para cada escola, tudo fecha. Só que fica muita escola, fica 72 escolas, né? E todas estão recebendo 10 ingressos. Isso eu componto. Todas aqui já estão com o
mesmo número de ingressos. E se ao invés de eu dar 10 ingressos para cada escola, eu dar 20 ingressos para cada escola. Aí eu não vou ter mais 72 escolas contempladas, né? Vamos lá. Se eu pegar esses 400 ingressos e dividir em pacote de 20, eu vou ter 20 escolas contempladas. Então são 20 escolas. Recebendo 20 ingressos cada uma, eu distribuo os 400 ingressos. E eu pego 320, faço a mesma coisa. 320 com pacotinho de 20, eu vou ter 16 escolas. recebendo 20 ingressos também consegui distribuir os 320. Olha que maravilha. Acabei de distribuir agora
20 ingressos por escola e agora eu só estou contemplando 36 escolas. Então isso é bom porque ele quer o número mínimo de escolas e eu acabei de eh melhorar a minha situação. Só que será que esse já é o número mínimo de escolas? 36 escolas? Não é. Você vai ver que para você chegar no número mínimo, você não tem que dar 20 ingressos para cada escola. O melhor que você pode fazer é dar o máximo de ingressos para cada escola. Você tem que achar o máximo divisor comum, o maior número que seja divisor tanto do
400 quanto do 320, tá? É, e que seja divisor dos dois ao mesmo tempo, né? E tu quer o maior número, tu quer o maior número que seja um divisor do 400, 320. Como que a gente calcula isso? Vamos usar lá o nosso método que eu disse que é o método que eu mais uso, né? Que é o método mais fácil, que é eu fazer a decomposição sucessiva em fatores primos. Ã, porém eu só vou colocar aqui fatores primos que dividam os dois, tá? Então, por exemplo, o dois é o menor fator primo que tem.
Ele divide os dois, divide. Esse aqui fica 200 e esse aqui fica 160. Vou botar o dois de novo porque ele divide os dois, fica 100 e fica 80. Vou botar o dois de novo porque ele divide os dois, fica 50, fica 40. Vou botar o dois de novo porque ele divide os dois, fica 25, fica 20. Vou botar o dois de novo, não. Não vou botar o dois de novo, porque o dois não divide os dois. O dois até divide 20, mas não divide o 25. Eu quero o MDC. Eu só posso colocar aqui
fatores que dividam os dois. O três divide os dois, não, não divide nenhum. O cinco divide os dois, divide. O cinco, divide os dois. Então vai dar cinco aqui e vai dar quatro aqui. Existe agora algum fator primo que divide os dois? Não existe mais. Não tem nenhum número primo que vai dividir os dois ao mesmo tempo. O dois só divide o quatro, o três não divide ninguém e o cinco só divide o cinco. Acabou. Não é questão de que, ah, ficou faltando. Não, não, não. É que a regra não é essa. A regra é
eu colocar aqui números primos, fatores primos que dividam os dois ou os três que estão aqui simultaneamente. E nesse caso aqui não tem mais nenhum número primo que divide esses dois simultaneamente. Acabou. Para eu achar o MDC, eu só multiplico todo mundo que tá aqui. 2 x 2 4 x 2 8 x 2 16 x 5, 80. O máximo divisor comum entre o 400 e o 320 é o 80. Entendeu? Ou seja, o que que que isso aqui é? Tem gente perguntando que o que que esse número significa agora? Significa que o maior número que
eu consigo pegar e dividir o 400 por ele e também dividir o 320 por ele é 80. Tô perguntando ali, mas o cinco não divide o cinco, mas criatura. Eu falei que eu tenho que botar um fator primo aqui que divida sempre os dois para achar o MDC. Pô, caramba. É claro que o 5 divide o 5. O 5 divide o 25 e o 20. Quanto que deu? O 25 virou 5 e o 20 virou o 4. Agora tem outro número primo que divide os dois ao mesmo tempo. Não tem mais. Acabou. Tô falando. Vocês
t que assistir isso aqui muitas vezes, cara. Tá beleza? Entendeu? Aí tem gente perguntando como que eu faço para diferenciar? Porque na questão pediu o mínimo, galera. Isso é a interpretação. Eu não sei se vocês perceberam, mas o que eu tava fazendo era isso. Eu tava explicando que como ele quer o menor número possível de escolas, isso quer dizer que eu tenho que dar o máximo de ingresso pra escola. Se eu der um ingresso para cada escola, eu vou ter 720 escolas. Vou pegar 400 ingressos, vou dar um para cada escola, vou contemplar 400 escolas.
Vou pegar 320 ingressos, vou dar um para cada escola, vou completar 720 escolas. Vou peg vai ter 720 escolas. Eu quero o menor número de escolas, então vou dar o máximo de ingresso para cada escola. Só que as escolas têm que receber sempre o mesmo número de ingressos, o mesmo número. Então tem que saber qual é o maior número que eu posso pegar o 400 e dividir por ele e o 320, mas que seja pros dois ao mesmo tempo. É o 80. Eu o maior pacote de ingresso que eu posso dar é um pacote de
80 ingressos. Tanto o 400 vai ser dividido por 80, certinho? E o 320 vai ser dividido por 80. E o 80 é o maior número pelo qual eu posso dividir ambos. Entendeu? É isso. Quer ver? Deu 80. O que que eu posso fazer agora que deu 80? Eu posso pegar, tá? Eu posso pegar o 400 e dividir por 80. Eu quero 400 ingressos divididos em pacotes de 80. Quantas escolas vou vão poder receber esses 80 ingressos? Cinco. Eu consigo montar cinco pacotes desse. O 320 dividido em pacotes de 80. Ou seja, quantas escolas recebem um
pacote de 80? Quatro. O menor número de escolas que eu posso contemplar são nove escolas, 5 e 4. E essa é a resposta. Nove. Entendeu? Sacou? Ah, Pedro, não entendi. Então você tá com lacuna intelectual severa. Se tu não entendeu aqui, eu te garanto, não existe nenhum lugar do Brasil mais em que você vai entender. O que você tem que fazer é, se você não entendeu, tu tem que ir lá na plataforma SAD, no ciclo de nivelamento e assistir todo o ciclo de nivelamento e assistir toda essa aula de novo. Quem não foi capaz de
entender agora com essa explicação, você tá isso, você tem que receber o diagnóstico para você entender. Você tá ferrado a cabeça. Você não teve educação na sua vida. Todo mundo cagou para sua educação. Ah, que coisa dura que você tá falando. Dura é o que a vida vai fazer contigo se ninguém te falar isso. Você vai ficar a vida inteira aí procurando emprego, nunca é contratado, tentando passar em concurso, nunca passa. Você vai falar que que tá acontecendo? Eu vou falar: "A culpa não é sua, meu filho. Você nasceu num país que tá no no
pior dos ranks de matemática e linguagem do mundo. Então, você tem que correr muito atrás. Eu tenho aqui o que você precisa para correr atrás, mas você vai ter que falar assim: "Eu preciso estudar muito, tá?" É isso. Beleza? OK. Vamos lá. Vamos pra próxima questão. Isso aqui não é para você ficar triste, é para você se motivar, para você falar: "Então, vou estudar mais ainda". É isso, pô. Tá, vamos lá. Enem 2014. Em uma plantação de eucaliptos, um fazendeiro vai aplicar um fertilizante a cada 40 dias, um inteticida para combater formigas a cada 32
dias e um pesticida a cada 28 dias. Pô, isso já me parece uma questão cíclica, né? Tem um ciclo de aplicação do fertilizante que é de 40 em 40 dias. Então ele vai aplicar no dia 40, no dia 80, no dia 120, no dia 160, no dia 200. tem um ciclo de aplicação do inteticida de formiga que é a cada 32 dias. Então ele vai aplicar no dia 32, 64, no dia 96, no dia 128. É 128. Tem um ciclo aqui do pesticida que é de 28 e 28 dias. Então ele vai aplicar no dia
28, no dia 56, no dia 84. Beleza? E ele já começou aplicando os três produtos no mesmo dia. Pá, hoje eu apliquei os três e agora? Agora, cada produto vai ser aplicado quando passar o seu período, que é o tempo. O que que é o período, né? Muitas vezes você tá estudando isso lá é ondulatório e não entendeu. O período é o tempo que demora para bater um ciclo. Então qual é o período do primeiro produto? 40 dias. Qual é o período do segundo produto? 32 dias. O período do terceiro produto? 28 dias. Beleza? OK.
De acordo com essas informações, depois de quantos dias, depois da primeira aplicação, os três produtos vão ser aplicados novamente no mesmo dia? Isso é o que que ele tá pedindo? Que que ele tá pedindo? Fala para mim. Não é claramente o MMC? Ele aplicou os três produtos hoje. Ele quer saber quando que vai encontrar de novo as três aplicações. Entendeu? Menina mandou aqui para mim a estatística. Em matemática, o Brasil ocupa a posição de número 65, 65ª posição no ranking, estando próximo de países como Jamaica, Argentina e Colômbia. É isso. O nosso nível de matemática,
linguagem é o mesmo nível da Zâmbia. Ah, filho. Tá. Então vamos lá, fica ligado, tá? Eh, então vamos lá. E aí, que que a gente faz aqui, tá? Que que a gente faz aqui? A gente faz o mmc, tá? A gente vai aplicar o primeiro, todos os produtos vão ser aplicados aqui num dia zero e a partir de agora cada produto tem ali o seu ciclo, OK? Então, o primeiro produto vai ser aplicado no dia 40, depois no dia 80, depois no dia 120, depois no dia 160. Esses aqui que eu tô escrevendo são o
quê? Responde para mim o que que é isso aqui que eu tô escrevendo? São os múltiplos, né? São os múltiplos, tá? Os múltiplos do 40, tá? Eu tô vendo aqui nos comentários que fica um monte de gente falando comigo, né? É engraçado, eu tô vendo alunos que chegaram na plataforma em novembro, né, no vitalício agora, e chegaram cheio de dúvidas, né, parecendo mesmo que estavam com eh uma sequela mental muito grande. E eu tô vendo agora eles respondendo tudo que eu tô perguntando certinho. É por isso que eu falo desse jeito, porque eu sei que
funciona, tá? Acreditem e estudem, tá? Vocês vão vencer se vocês acreditarem e se vocês estudarem de verdade, vocês vão ficar inteligentes. Mas se não se não estudarem de verdade e não prestarem atenção de verdade, vocês vão ficar burros para sempre. Pode ter certeza, tá? para sempre mesmo. Burrice não sai fácil. OK, vamos lá. E tem muita gente me fazendo outras perguntas. Então, o seguinte, eu respondo as perguntas que eu quero. Eu não posso responder todas as perguntas. Tem uma menina aí que tá cheia de dúvida em coisas básicas e tá me fazendo uma pergunta que
repetidamente. Eu só vou te dizer uma coisa, moça. Enquanto você tá me fazendo essa pergunta repetidamente, você tá deixando de prestar atenção no que eu tô explicando aqui agora. Essa pergunta sua é uma curiosidade, não é pertinente para agora. Presta atenção no que eu tô explicando, porque ela tá aqui já me dando esporro. Você não tá me respondendo. Você não Por favor, presta atenção aqui no que eu tô explicando agora. Tá? É pro seu bem. Se eu for responder todas as perguntas que me fazem, é só você ver, tem 400 pessoas na aula. Vou ficar,
eu não vou conseguir dar aula, tá? Vamos lá. O segundo produto que tem um ciclo de 32 dias, ele vai ser aplicado no dia 32, depois vai ser aplicado no dia 64. Só tô exemplificando, vai ser aplicado no dia 96, depois vai ser aplicado no dia 128, depois vai ser aplicado no dia 160, depois vai ser aplicado no dia 192 e por aí vai. E o terceiro produto que em ciclo de 28 dias vai ser aplicado no dia 28, depois vai ser aplicado no dia 56, depois vai ser aplicado no dia 84, depois vai ser
aplicado no dia 112, depois vai ser aplicado no dia ã 120 140, depois no dia 168 e por aí vai. Pô, você já vê que eu eu escrevi os múltiplos deles e será que eu já consigo encontrar o menor múltiplo comum de todos eles? Cara, não, eu até consigo ver que tem o 160 aqui, mas eu quando eu falo múltiplo comum, eu quero de todo mundo, de todos envolvidos, né? Eh, então o 160 é o menor múltiplo comum entre o apenas entre o 40 e o 32, né? Ã, e aí, cadê? E agora que que
eu faço, né? É aquilo, esse método aqui de você contar os múltiplos é muito ineficiente. A gente vai usar um método mais sofisticado, tá? A gente vai usar um método que funciona melhor, mas vocês conseguiram entender o propósito, né? Dá para ver que é mínimo múltiplo comum. Eu tô querendo ver quando que eles vão se encontrar, quando que o os múltiplos vão se encontrar, que eu vou est aplicando os os vou est aplicando eh os fármacos, né, os defensivos agrícolas simultaneamente, tá? É simples. Eu tenho que fazer o mmc entre esses três números. Então vamos
lá. MMC entre 40, entre 32 e entre 28. Eu simplesmente vou começar a dividir pelos fatores primos do menor pro maior. Então menor fator primo aqui é dois. Faz a divisão. Independente se todo mundo é divisível por ele ou não. É pro MDC que todo mundo tem que ser divisível. Pro mmc é só atacar aqui o menor fator primo. Pelo menos um tem que ser divisível por ele. Tá aqui os três são maravilha. Então aqui 16, aqui 14, boto o dois de novo, né? Aqui vira o 10, aqui vira oito, aqui vira o sete. Boto
o dois de novo. Ai, mas o sete não é divisível por dois, não interessa. O 10 e o 8 são pelo menos um. Aí, então aplico aqui fica cinco, aqui fica quatro, aqui fica sete. Boto dois de novo. Só pelo fato do quatro ser divisível pelo 2, eu preciso me manter no dois até eu ter matado tudo que o dois participa, tá? O cinco não sofre divisão, o quatro vira dois e o sete não sofre divisão. Que que eu boto aqui agora? O dois de novo. O dois de novo. É aqui que vocês vão errar.
Vocês vão ver o quatro, vocês vão querer botar logo cinco. Não, tem que matar todos os fatores de dois primeiro. Bota o dois de novo. Agora tu mata esse. O cinco não sofre divisão, sete não sofre. Agora o próximo número primo que divide um cara aqui não é o três, porque ninguém aqui é divisível por três, é o cinco. Então tu matou aqui o cinco também, ele virou um. O um continua aqui e o sete não sofreu nenhuma divisão ainda. Bota o sete aqui agora, todo mundo continua um, mas o sete também vira um. Pronto,
agora sim o mmc vai vir do produto de todo mundo que tá aqui, tá bom? Então vamos lá. 2 x 2= 4 x 2 8 x 2 16 x 2 32. 32 x 5, metade de 320, 160. 160 x 7, 7 x 7 x 160, 700 + 420, 1120, ok? 1120. É isso. O mmc é 1120. Lembra aqueles múltiplos que eu tava fazendo? Você lembra que eu tava assim, ó, 40, 80, 120, 160, 200. Lembra? Eu tava fazendo por 32, por 28. Eu só ia conseguir encontrar um número que aparecesse nos três no 1120. Quanto
tempo eu ia levar para escrever até o 1120 nos três? Tá maluco, né? Tá doido. Perguntaram cadê a alternativa? Oxe, também quero saber cadê a alternativa. Cadê 2 x 2? 4 x 2 8 x 2 16 x 2 32. 32 x 5 160. O 160 x 7. Será que foi aqui que eu errei? 700 + 420. Não, É, é 1120. Cadê? Essa aqui é uma questão do Enem. Oxe, tem alguma coisa errada nas alternativas. Cadê essa questão aqui? É 1120, pô. Tem alguma coisa de onde eu peguei a questão, alguém alguém errou nas alternativas, né?
Depois de quantos dias após a primeira aplicação, os três vão ser aplicados novamente no mesmo dia? Fazendeiro aplicará a cada 40, a cada 32, a cada 28. Ele iniciou aplicando os três produtos em o mesmo dia. Não vou é é algum erro aqui na questão, né? Algum erro aqui na na escrita ali, ó. Falaram assim, ó. Falaram: "Tá errado mesmo. A letra D, ela deveria ser 1120 na questão oficial do Enem, né? É isso mesmo. Alguém de onde eu peguei na internet, né? Porque eu não eu não montei a apostila aqui oficial, peguei na internet
essa questão. Eh, alguém escreveu a alternativa errada. Tá bom, galera? Mas a resposta é 1120 mesmo, tá bom? É de fato 1120. É que o print da questão é que tá com uma alternativa errada, tá bom? Eh, perdão aí, tá bom? Mas o bom é que todo mundo aqui falou, né? Todo mundo disse: "A questão tá errada, é 1120." Essa é a resposta é 1120. Tá bom? Vamos pra próxima. Rodrigo estava observando o o pisca pisca ã do enfeite natalino de sua casa. Esse pisca pisca é composto por lâmpadas amarelas, azuis, verdes e vermelhas. São
quatro cores de lâmpadas. Rodrigo notou que lâmpadas amarelas acendem a cada 45 segundos. Ó, já dá para ver que é um ciclo, né? É o período que a lâmpada acende é de 45 em 45 segundos, tá? Lâmpadas verdes acendem. Só um instantinho aqui. Pronto. Lâmpadas verdes acendem a cada 60 segundos e azuis a cada 27 segundos. E as vermelhas ele não falou. As vermelhas, ele falou assim: "Elas só acendem quando as lâmpadas das outras cores estão acesas ao mesmo tempo". Então a vermelha ela acende o quê? Quando todas as outras três estão acesas ao mesmo
tempo. Pô, né? De quantos em quantos minutos as lâmpadas vermelhas acendem? Já dá para saber que é uma questão de mmc. E eu sei aqui, né, que uma das lâmpadas ela vai acender a cada 45 segundos. A outra acende a cada 60 segundos, a outra acende a cada 27 segundos, mas tem uma lâmpada que acende só quando as três estão acesas. Ou seja, ela só acende nos múltiplos comuns. A outra lâmpada só acende quando essas três estão no múltiplo comum, tá? Detalhe, né? Como é que eu vou saber a Olha isso, olha como é que
conecta com aquela aula de MMC que eu dei, né? O primeiro exemplo, eu falei assim da do remédio de 12 em 12 horas. Eu falei: "Quando você acha o MMC que é 12, você sabe que agora a cada 12 horas você vai dar os remédios juntos. Então quando eu encontrar o MMC aqui desses três números, quando eu encontrar eu vou saber que a cada vez que esse mmc se repete, a cada vez que esse padrão se repete, eu tenho sempre ali as três lâmpadas acesas. Eu tenho sempre a lâmpada vermelha acesa por consequência. Entendido todo
mundo? Sim. Então agora eu vou pra execução, vou achar aqui o mmc entre esses três números, tá bom? E vou usar o método que que a gente mais tá usando aqui, né, que é o método que eu prefiro, que é fazer a decomposição simultânea por fatores primos, OK? Então vamos lá. Vou começar colocando aqui um dois, né? Por quê? Porque é o menor fator primo possível e o 60 é divisível pelo 2. Então se pelo menos um é divisível pelo 2, eu vou usar o dois, tá? Então o 45 não sofre essa divisão, o 60
vira 30 e o 27 não sofre. Eu boto o dois de novo só por causa do 30. Então o 45 não sofre, o 30 sofre, o 27 não sofre. Agora sim, eu esgotei as possibilidades do número dois. Eu vou botar o três. Mas alguém é divisível pelo três? Sim, todos são. Ótimo. Mas se pelo menos um fosse, eu já botaria o três também, tá? 45, 15 vira 5, 27 vira 9. Eu vou botar o três de novo, tá bom? O o 15 vira cinco, o cinco não reage e o 9 vira três. Vou botar o
três de novo só por causa desse cara aqui que vira um e os cinco não reagem. Agora eu boto cinco. Matei todo mundo aqui. MMC o quê? 2 x 2 4 x 3 12 x 3 x 3 é 108. e vezes 5 540. OK? Então, a cada Vamos lá. Primeira coisa, né? Se as lâmpadas foram acesas juntas no momento zero, depois de 540 segundos, é o primeiro momento em que elas se acendem juntas, OK? Depois de 540 segundos. Agora, a cada 540 segundos, elas também vão se acender. A cada 540 segundos, elas vão repetir. Então,
de 540 em 540 segundos, as lâmpadas acendem e por consequência a vermelha acende, né? Porque a vermelha acende quando as três estão acesas. Entendido? OK. Só que ele pergunta de quantos em quantos minutos as lâmpadas vermelhas acendem? Eu já sei que elas acendem a cada 540 segundos, mas 540 segundos são quantos minutos? Tá? É óbvio, você poderia falar assim, ó, 1 minuto são 60 segundos, então 540 segundos são quantos minutos? E executar aqui uma regra de três, né? X x 60. Beleza? Mas eu também queria que você tivesse já o raciocínio direto de falar assim:
"Olha, 540 segundos divididos em pacotes de 60 segundos, eu vou descobrir quantos minutos eu tenho." Então, simplifica por 10, né? 54/ 6 dá 9, tá? Então, a resposta é a cada 9 minutos. Entendido, galera? Beleza? A cada 9 minutos. Vamos lá. Uma indústria de tecidos fabrica retalhos. Deixa eu só diminuir minha caneta um pouquinho aqui. Fabrica retalhos de mesmo comprimento, né? Retalho de mesmo comprimento. Após realizarem os cortes necessários, verificou-se que duas peças restantes tinham as seguintes medidas, tá? Então, eles têm ali e duas peças de retalhos, né? Duas peças de tecido e uma tá
com 156 cm e a outra tá com 234 cm. OK? Uma tá com, ou seja, só para deixar claro, 156 cm é uma peça grande, né? 1,56 m e 234 cm é 2,34 m. O gerente de produção sem formar dessas medidas deu a ordem para que um funcionário cortasse esse pano em partes iguais. Eu quero, não interessa se você tem aqui um pedaço de de 156 cm e outro de 234. Não interessa. Eu quero que isso tudo vire pedaços de pano idênticos e de maior comprimento possível. Então, eh, ah, tu tu trabalha na fábrica, você
fala assim: "Ah, beleza, chefe. Vou pegar aqui o tecido de 156 cm, vou pegar aqui o tecido de 234 cm, vou cortar tudo em pedacinho de 1 cm. Tu vai chegar lá, vai estar com 360 pedaços de 1 cm. Vai falar assim: "Estão todos iguais, você vai ser demitido, né?" Porque ele disse que ele quer que esses pedaços tenham o maior comprimento possível. E 1 cm não é o maior comprimento possível, até o menor comprimento possível, na verdade, tá? Ah, vou cortar, chefe. Tudo em pedaço de 2 cm também funciona, mas aí será que 2
cm é o maior pedaço que tu consegue, tá? Ã, é claro que você vai ter que fazer o MDC. Você precisa saber qual é o maior divisor comum para esses dois tecidos aqui, né? Pô, será que eu consigo cortar cada um deles em pedaços de 4 cm? É, certamente consigo, mas eu quero o maior. Eu quero realmente o maior. É. É o maior possível, tá? Eh, pedaço de 6 cm dá também, mas eu quero o maior possível. Quero que fique os maiores pedaços idênticos, tá? Eu só quero fazer uma pergunta para vocês, para forçar a
inteligência de vocês, tá bom? E eu tenho certeza que essa pergunta não é uma pergunta tão simples assim. Quando ele disse aqui, ó, eh, o funcionário cortasse o plano em partes iguais de maior comprimento possível, você consegue elaborar outro enunciado que dissesse a mesma coisa, que também dissesse o mesmo critério? Partes iguais de maior comprimento possível. Como isso poderia ser reescrito para gerar a mesma pergunta? Eu quero a menor quantidade de pedaços. Eu quero o menor número de peças. Entendeu? Olha, agora você conectou. Lembra que na questão das escolas ele não falou assim: "Eu quero
dar a maior quantidade de ingressos para aquela escola". Não, ele falou: "Eu quero que o menor número possível de escolas seja contemplada". Aí a gente inferiu que se é pro menor número possível de escolas ser contemplada, eu preciso dar mais ingresso para todas as escolas. Eu tô te falando, eu não acho que nenhuma aula um professor tenha tenha dito esse tipo de coisa, tenha feito esse tipo de exercício. Isso é muito raro de alguém fazer. Aí às vezes eu tô aqui explicando e tem algum aluno ali me perguntando alguma coisa, ai não me responde, não
me responde. Que é isso, cara? Né? Ó o que eu tô falando aqui. Isso aqui que é importante de verdade para você ganhar velocidade interpretativa, tá? Ou uma forma de dizer o maior comprimento possível ou lá dizer o maior número de ingressos por escola, ou também o menor quantidade de planos possíveis ou o menor número de escolas que foi o que dito lá, entendeu? Sacou? Deu para pegar, né? Ótimo. O que importa é o seguinte, eu já percebi que eu preciso dividir esses pedaços de pano em pedaços iguais e que sejam os maiores pedaços possíveis
ou que gerem o menor número de peças possíveis. OK? O MDC claramente, né? Qual é o maior divisor comum para esses dois números aqui? O 156 234. 156 e 234. Vou agora executar aquele meu método, né? Vou colocar aqui o dois porque o dois divide ambos. Então eu só posso colocar aqui fatores primos que dividam todos. O dois divide ambos, né? Então vou fazer isso. Vou colocar o dois aqui, né? O resultado aqui da divisão, né? Metade de 140 seria 70 e de 16 é 8. Então 78. Metade de 234 dá 117. Posso colocar o
dois aqui. Afinal de contas 78 divisível pelo 2, né? Não. Eu só posso admitir aqui fatores que dividam todo mundo. O dois não divide todo mundo. Posso colocar o três aqui. O 78 é divisível pelo 3. É só você somar 7 + 8 dá 15. 15 é divisível por 3. Então 78 também é. 117 soma 1 + 1 + 7 dá 9. 9 divisível por 3. Então 117 também é. Ótimo. Eu tô colocando aqui um fator primo que divide todo mundo. Maravilha. Vou executar a divisão. 78 por 3 a gente faz 60 depois 18, né?
60 dá 20, 18 dá 6, 26. 117 di por 3. Se fosse 120 daria 40. Como é 117, tem que tirar um, vai ficar 39. Beleza? Nada que eu tô fazendo aqui, nenhuma técnica matemática é novidade, tá? Tudo já lá no ciclo de nivelamento, tá bom? No alfabetização matemática ou no módulo fundamento da matemática, que é o novo nome dele, tá? Então, só para deixar claro. Posso colocar agora eh o dois aqui? Claro que não, né? Eu não vou nunca retroceder, mas só para mostrar, né? Tem que ser alguém que divide os dois. O dois
não divide os dois. Nem mesmo 3 divide os dois, né? É, o 39 é divisível pelo 3, mas o 26 não é, então não pode. Tem algum número primo que vai dividir esses dois agora simultaneamente? O 5 divide eles dois? Não. O 7 divide eles dois? Não. Eu preciso de um número primo que divida os dois. Próximo número primo depois do sete. Hum. Estão falando ali que o 39 é primo, né? Tá errado. Próximo número primo depois do sete 11. 11 só é divisível por 1 e por 11, mas não dá para dividir eles por
11. 13. 13 é primo. 13 é primo. E os dois podem ser divididos por 13. 26 por 13 inclusive dá 2 e 39 por 13 dá 3. Agora sim, não tem mais nenhum número primo que eu possa botar aqui para matar os dois ao mesmo tempo. Multiplico aqui 2 x 3 6. 6 x 13 6 x 10 60. 6 x 3 18 78. Ou seja, eu posso pegar esses pedaços de pano e cortar em fatias de 78 e vai dar certinho. Percebeu? Eu pego aqui o pedaço de de 156. Tá vendo aqui o pedaço de
156 cm que tem na fábrica? Eu divido ele num pedaço de 78 e em outro de 78. Esse é o maior pedaço que dá para dividir, que vai dividir também ao mesmo tempo, né? O pedação de 234. Eu pego esse pedaço de 234, divido aqui, ó, 78 aqui, 78 aqui, 78 aqui. Pronto, tô transformando tudo em pedaços idênticos de 78. E isso aqui vai gerar o menor número possível de pedaços ou os pedaços com maior comprimento possível. Tá resolvido a questão. Pegou? Que que pode atrapalhar você a fazer tudo isso aqui? Essa técnica é o
de sempre. Vamos ser sincero, de tudo que vocês estão vendo nessa aula, o que que vai quebrar a maioria esmagadora e, infelizmente, inclusive de vocês? Não sei tabuada. Não sabe tabuada. Quantos aqui dessa aula que estão aqui agora assistindo, será que fizeram o que eu mandei? Falei: "Aprenda a tabuada em um dia. Aprenda a tabuada loucamente. Veja várias vezes a tabuada. Fique falando a tabuada. Se você não fez, é você mesmo que tá construindo teu fracasso. Me perdoa. É isso. Em um, 2, 3, 4, 5 dias qualquer pessoa domina tabuada por completo, entendeu? Não, não
pode não saber a taboada. Se você não, se você está se recusando a fazer isso, eu vou ver você de novo aí no meio do ano, faltando três meses para você vai estar perguntando o que que eu faço. Ainda tô acertando 21 em matemática, 25. Você não não tá tendo humildade de seguir o o cronograma, de seguir o que eu tô falando para fazer, entendeu? Tem que ter, pô. Senão você vai ficar travando. Eu avisei isso, falei, se você não aprender tabola, você vai travar em tudo. Você não vai se desenvolver em matemática. Não vai
ser surpresa. Você não aprendeu tabol realmente não tá se desenvolvendo. Dito e feito. Tá bom? Vamos lá, então. Então, bora, tá? Eh, bora. Uma empresa eh de logística é composta de três áreas. Uma é administrativa, outra é operacional e uma de vendedores. A área administrativa tem 30 funcionários, a operacional 48 e a de vendedores tem 36 pessoas. No final da ano, a empresa realiza uma integração entre as três áreas de modo que todos os funcionários participem ativamente. Então ela junta essas três áreas, né? As equipes devem conter o mesmo número de funcionários com o maior
número possível. Olha isso. Ele tá dizendo que ele pega todos os funcionários da empresa, né? A empresa tem aqui, ó, 30 funcionários de uma certa área. Ela tem 48 funcionários de outra e tem 36 de uma. Ela junta todo mundo numa sala e redesenha as equipes para eles se integrarem, entendeu? Né? E aí ele faz o seguinte, ó. Elas têm que ter todas o mesmo número de funcionários, equipes idênticas. Equipes idênticas, tá? E o maior número possível, ou seja, o menor número possível de equipes para que cada equipe fique com o maior número, tá? Determine
quantos funcionários devem participar de cada equipe e o número possível de equipes. Beleza? Vamos ver então. Ã, que que a gente faz aqui, né? A gente faz, claro, o MDC. A gente quer pegar esses funcionários e redividir eles em equipes menores, tá? A gente quer pegar e redividir eles em equipes menores. Tudo bem? Então, vamos lá. Eh, questão meio mal formulada, tá bom? Tô falando aqui para vocês porque eu não não eu peguei ela, né, mas eu não tinha percebido isso. Eu tô vendo agora, né, meio mal formulada porque ela é um pouco ambígua, tá
bom? Então eu vou só complementar ela aqui para vocês, tá bom? Só para não ficar uma coisa eh meio zoada. Eh, o que tem que ser feito nessa questão aqui, o que deveria estar no enunciado, é que as equipes vão ser redividas em equipes menores para facilitar a integração, tá? E essas equipes, elas têm que manter ali o mesmo perfil de funcionários. Elas têm que cada equipe ainda tem que ter o seu a mesma o mesmo perfil de funcionários, tá bom? tem que manter ali o mesmo número que já o mesmo tipo de funcionário. Tem
que continuar tendo uma equipe ali que é feita só de equipe administrativa, uma só operacional e uma só de vendedores, tá bom? Então vamos lá. Eu vou pegar esses números aqui e vou tirar o MDC entre eles, tá bom? Vou descobrir agora qual é o máximo divisor comum entre eles, como é que eu posso redesenhar as equipes sendo todas as equipes iguais? Então vamos executar ali o métro, né? O dois ele divide todo mundo aqui. Para ele entrar aqui, ele tem que dividir todos aqui, sim. O dois divide, tá? Então ele o 30 vira 15,
o 48 vira 24 e o 36 virou 18. Eu posso colocar o dois novamente aqui? Não, ele deveria dividir todo mundo, mas ele não divide o 15, então eu já não posso botar o dois aqui, tá bom? Posso botar o três. O três eu posso porque o três divide todo mundo. Então aqui vira cinco, aqui vira oito e aqui vira nove. Eh, e agora quem eu posso botar aqui de número primo que divida todos ao mesmo tempo? Não tem nenhum. Não dá para eu colocar aqui um número primo que divida todo mundo ao mesmo tempo,
tá? Não dá. Ah, o 18 vira 6, perdão. 18/ 3 dá 6. Mas não dá para colocar o dois não vai dividir todo mundo aqui, o três não vai, o cinco não vai, não tem um número primo que vá fazer isso. Então é 2 x 3, 6. Eu posso redesenhar isso aqui em equipe de seis, tá bom? Quantos funcionários devem participar de cada equipe? Seis. E o o número possível de equipes, você pode pegar o primeiro setor de 30 equipes e você pode, é, você pode pegar o primeiro setor de 30 equipes e dividir ele
em em grupos de seis. E aí ele vai dar cinco, cinco equipes de seis. O 48, quando você dividir pelo 6, vai dar o quê? Oito equipes. E o 36, quando você dividir por seis, que é o número de equipe, vai dar seis equipes. Então quantas equipes são? 13 + 6, 19 equipes de seis pessoas. Entendeu? Percebeu? Mas assim, questão não tá bem formulada, questão assim meio meio pai, eu não estaria no Enem essa questão, tá bom? Essa aqui é do Enem. Pronto. Essa aqui agora é boa do Enem, tá bom? Tem mais tem mais
duas pra gente fazer aqui pra gente fechar essa aula. Vamos lá. Ã, aquilo ali não é um resto não, galera. Isso aqui não é resto não. Tá bom? o que aparece ali no no MDC que no final não é dividido, não é nada não. Para você se preocupar, aquilo ali não é um resto, tá? Então vamos lá. Aquilo ali é, na verdade, o número de equipes mesmo, né? Já tinha aparecido ali. Aquilo ali, os números que sobram, sem ser divididos, aquilo é o número de equipes, tá bom? Ã, então vamos lá. São 19 equipes de
seis pessoas. Bora. Ã, vamos lá. Agora essa questão aqui é uma questão boa, tá? É até uma questão de alto nível, tá? Não é uma questão facinha do Enem, não. Muita, muita, muita gente errou mesmo, tá bom? E quem, quem acertou também, muita gente perdeu tempo nela. Então, vamos lá. Ah, um arquiteto está reformando uma casa de modo, pronto, de modo, que que houve aqui? Pronto, de modo a contribuir com o meio ambiente, ele decide reaproveitar tábuas de madeira retiradas da casa. Então, olha isso aqui. Essa questão vai misturar algumas coisas. Ele tem 40 tábuas
de 540 cm, que são 5, então são tábuas bem grandes, né, de 5,40 m. E ele tem 40 dessas. Ele tem 30 tábuas de 810 cm e 10 tábuas de 1080 cm. Então, ã, todas da mesma largura e espessura. Quer dizer, só que elas são iguais, exceto pelo seu comprimento. Beleza? Entendido, né? Ele pediu a um carpinteiro que cortasse essas tábuas em pedaços de mesmo comprimento, sem deixar sobras, tá? Ou seja, o que que quer dizer sem deixar sobras? Divisões exatas, tá? E de modo que as novas peças ficassem com o maior tamanho possível. Ele
quer que as novas tábuas tenham o maior tamanho possível, maior. Sejam tábuas grandes, porém de comprimento menor do que 2 m. Mas lembrando, ele quer que todas as tábuas sejam iguais. todas as tábuas idênticas, ã, e quer que elas sejam ao mesmo tempo muito grandes, quer que elas sejam. Então, você não pode chegar aqui e falar assim: "Ah, todas as tábuas de 540 cm vamos dividir tudo em tábua de 1 cm e as de 810 vamos dividir em 1 cm também. E as de 1080 a gente divide em tábua de 1 cm." Vão ficar 1080
tábuas de 1 cm e aí todas estão iguais. Mas ele falou que ele quer com o maior comprimento possível. Mas detalhe, é o maior comprimento possível, mas ao mesmo tempo que não passa de 2 m. Olha que sinistro. É muita coisa ao mesmo tempo na questão, né? E outra coisa, ele falou que ele tem, aí ele pergunta assim, ó, quantas tábuas vão ser produzidas, né? Ele quer saber. No final das contas, ele quer que você some o número de tábuas e diga quantas quantas vão ser produzidas. Galera, primeira coisa, você tem que ter a sabedoria
nessa questão de ignorar completamente o número de cada tábua. Ah, 40 tábuas de 540 cm. E daí que são 40? Ah, 30 tábuas de 810 cm, 10 tábuas de 1080. Você não pode se preocupar com isso. Não pode. Você tem que se preocupar com isso aqui, ó. Pensar aqui, ó. Olha, existem aqui. Oxe, tá saindo bugado aqui, ó. Tem que se preocupar com isso aqui, ó. Caramba, mano. Que dificuldade para eu desenhar aqui o retângulo. Deixa eu fazer aqui. Pronto. Existe aqui uma tábua. Agora vai. Tá fora de escala. Tá pronto? É isso aqui que
você tem que preocupar. Tem tábua de 540, tábua de 810, tábua de 1080. Tábua de 540, tá de 810 e tábua de 1080. É isso que é com isso que você tem que se preocupar. Ah, são tantas tábuas, são 40 tábuas dessa primeira, 30 da segunda e 10 terceira. Isso não interessa. Isso aí a gente vai ver depois. Por que que isso não interessa? Porque a primeira coisa é você entender o seguinte, você vai ter que pegar essas tábuas e cortar elas em pedaços de mesmo comprimento. Você vai ter que fazer com que elas gerem
tábuas idênticas no final das contas. E você quer que esse comprimento das tábuas finais sejam todas idênticas, né? E seja o maior comprimento possível, mas não passe de 2 m. Então, primeiro você vai ter que descobrir qual vai ser. Eh, você vai ter que descobrir o seguinte, uma tábua dessa de 540 vai virar quantas tábuas? Mas para eu saber isso, eu preciso saber qual vai ser o tamanho da tábua final. Você entende? Vamos supor que você falasse assim: "Olha, no final essa tábua 270 cm". Vamos supor que você falasse isso, as tábuas finais vão ter
270. Aí, maravilha. Eu já ia descobrir que a tábua de 540 ia virar o quê? Duas tábuas. Você concorda? Duas tábuas de 270. Sim. Aí agora eu ia descobrir se cada tábua de 540 vai virar duas tábuas de 270 e o cara que tem 40 tábuas de 540, cada uma vira duas, ele vai ter 80 tábuas só aqui. Só aqui ele já tem 80, entendeu? E a tábua de 210, ela vai ser dividida em tábuas de 270. E dá para dividir, né? 810 dividido por 270 dá três tábuas. Pode fazer a divisão aí. Você vai
ver 270 aqui, 270 aqui, 270 aqui. Então cada tábua de 810 vai virar três tábuas. Mas ele tem quantas de 810? Ele tem 30 de 810. Então 3 x 30. Só que ele já tem mais 90 tábuas. E a de 1080 vai dar quatro tábuas de 270. Então cada uma de 1080 vai virar quatro tábuas. Mas ele tem quantas de 1080? Ele tinha 10. Então só aqui tem mais 40 tábuas. O problema é que tu vai falar: "Pedro, olha só, mas o 270 aí deu certo, né? Porque todas elas foram divididas pelo 270." É, mas
ele disse que não podia passar de 2 m. Então aí já tem o primeiro problema. OK? Então vamos executar a questão agora. A execução é a seguinte. Primeira coisa, eu preciso descobrir qual é o MDC, qual é o maior valor possível que eu posso pegar nessas tábuas e dividir elas para gerar tábuas desse tamanho. OK? Primeira coisa é isso. Eu vou calcular o MDC. Eh, quem não pegou alguma coisa dessa parte, a menina falou, fica tranquila, vai pegando agora que você vai entender, tá bom? Vai, vai fazendo a questão junto comigo. Eu preciso descobrir o
seguinte, tendo tábua de 840, de 540, 81080, qual é um tamanho que eu posso padronizar essas tábuas? Um tamanho que eu posso fazer todas as tábuas ficarem com esse tamanho e que seja o maior tamanho possível também, porque eu quero o maior tábua possível, tá? Depois eu vejo se ele passou os 2 m ou não. Vamos descobrir o MDC. Vamos. 540. Deixa eu fazer aqui embaixo, tá bom? MDC entre 540, 810 e 1080. Tá? Só para deixar claro, eu não costumo usar muito macete assim nessa parte, né? Porque tem gente que fala assim: "Eu já
divide todos eles por 10 e já coloca 2 e cinco aqui. Funciona, mas eu não costumo fazer assim. Eu gosto de fazer bem tradicional mesmo, tá bom? Então vou começar botando aqui o dois que divide todo mundo, tá bom? Então esse cara aqui vira 270, esse cara aqui vira 405, esse cara aqui vira 540. Vou botar o dois de novo porque o dois divide todo mundo. Opa, não divide o 405 não divide pelo 2. Já não posso botar o dois. Eu só posso para achar o MDC, eu só posso botar fatores primos que dividam todos.
O três divide todos. O 270 é claro que dá para dividir por três. O 405 também, porque tu soma o 4 + 5 dá 9. O 540 também dá, porque soma 5 + 4 dá 9. Critério de divisibilidade. Então vou botar o três aqui. Aqui virou 90. Ótimo. Aqui virou ã 135. Eu dividi 390, depois dividi 15, né? Aqui vai virar o quê? Se fosse 600 daria 200. Então vai dar 180, porque eu tirei 60, tirei 20 de cada parte da divisão, tá? E aí posso colocar o três aqui agora? Todo mundo aqui é divisível
por três? Sim, todos são divisíveis por três, né? O 90 é o 135 e 180 também é, né? O 135 eu somo 1 + 3 + 5 dá 9. Então aqui vai dar 30. Legal. Aqui vai dar 120 e 15 5.5. Então 45, né? Eu divido o 120 depois o 15 e aqui vai dar 60. Posso botar o três de novo? Posso? Porque todo mundo é divisível por três, né? Maravilha. Todos são divisíveis por três. Então aqui o 30 dá 10, aqui o 45 dá 15 e aqui ã o 60 dá 20. Maravilha. Posso dividir
por três de novo? Não posso. Não posso. Tem algum número primo que eu posso colocar aqui e vai dividir todos eles? O dois e o tr a gente já sabe que não dá. Já esgotei eles. Tem o cinco, né? O cinco vai fazer esse cara virar dois. O cinco vai fazer com que esse cara aqui que é o 15 vire 3. E o cinco vai fazer com que esse cara que é o 20 vire 4. Acabou. Não tem mais nenhum número prima que eu posso colocar aqui para dividir todos ao mesmo tempo. Então o MDC
vai ser isso aqui. O MDC vai vir desse produto, tá? 2 x 3= 6 x 3= 18 x 3= 54 x 5 270. O mdc entre esses três caras é 270. Ou seja, o maior divisor comum para essas três tábuas é 270. Eu posso pegar essas tábuas aqui e o que que eu posso fazer com elas? O maior eh o maior divisor que eu posso aplicar para que elas tenham o tamanho desse divisor, né? Para que elas sejam divididas em grupos desse divisor, ou seja, grupos de 270, é o 270, né? Ele é o ele
é o que eu posso fazer em todas elas ao mesmo tempo. É claro que o 540 vai gerar o quê? Duas tábuas desse tamanho. É claro que o 810 vai gerar o quê? Tô vendo aqui três tábuas desse tamanho, né? Se eu dividir 540 por 270, eu obtenho essa resposta que é o dois. Beleza? É. É. Então, 810 vai gerar três tábuas dessa e o 1080 vai gerar o quê? Quatro tábuas de 270, tá? O único problema, então, só para dizer assim, primeira coisa, né, galera, esses números aqui que sobram, eles são isso. Se vocês
perceberem, esses números que sobram, eles são justamente isso, né? Se você pegar o 540 e você tiver dividido ele por todo mundo aqui, ou seja, você tiver dividido ele por 270, porque tu dividiu ele por 2, por 3, por 3, por 3, por 5, tu dividiu por 270, quanto que dá? Dá dois. Então, tu já tem essa resposta, né? que ele o o 540 pode ser dividido em duas tábuas de 270, o 810 pode ser dividido em três tábuas de 870 e o 1080 em quatro tábuas de 270. Agora, o que que você faria? Você
ia dizer assim: "Olha, mas pera aí, eu tinha 40 tábuas dessa aqui. Deixa eu botar, tem outra cor aqui para ficar mais. Eu tinha 40 tábuas dessa, depois eu tinha 30 tábuas aqui e eu tinha 10 tábuas aqui. Então, se cada tábua dessa aqui vai virar duas, né, quanto que é 40 x du tábuas? Aqui eu tenho 80 tábuas. Cada tábua aqui das 30 vai virar três. Então 3 x 30 dá 90 tábuas. E cada uma dessas tábuas vai virar quatro. Então 10 x 4 dá 40 tábuas. Então 80 + 90, 170 + 40, 210
tábuas. Marca aqui e erra a questão. Errou. Porque ele tinha botado uma condição. Ele tinha dito assim, ó. Tinha dito assim, ó, você não pode fazer uma tábua maior do que 2 m. Falou que 2 m era o limite pra tábua. Você fala assim: "Ah, Pedro, mas o MDC é 270". Eu sei, meu filho, mas é que ele tá pedindo uma articulação. Ele não quer que você aplique cegamente o MDC. Eu vou MDC é 270. Tá bom? Então, o maior número que você vai poder aplicar e que você vai poder dividir essas tábuas por esse
número é o 270. Mas e agora que o 270 não serve por uma condição do enunciado? Ele falou assim, ó, tem que ser menor que 2 m. Como é que você acha agora? Você que você concorda comigo que você teria que achar o segundo MDC, você teria que achar o segundo maior divisor comum. Quem é o segundo maior divisor comum? É, tem que ser um outro número que você também consegue pegar tanto o 540, 81080 e dividir por esse número os três. Como é que você faz isso para você achar? Você deixa de multiplicar pelo
menor dos números que tá aqui. Por exemplo, de onde veio o 270? De todas essas multiplicações. E se você deixasse de ter multiplicado pelo 2, você não tivesse multiplicado pelo 2, ou seja, você pega o 270 e você divide pelo 2 para tu reverter. Ou você só pega aqui, ó, 3 x 3, 9 x 3, 27 x 5, dá o quê? 135. 135. Então, ou seja, dá para eu pegar essas três tábuas aqui e dividi-las em pedaços de 270. Mas e se eu não quiser fazer isso? A outra possibilidade que vai funcionar para todas é
135, entendeu? Que aí eu pego aqui o 270, tá? E eu corto ele também em duas tábuas. Aí ele vai ficar 135, 135. Eu pego aqui o 270. Cada 270 eu vou dividir em mais duas tábuas, tá bom? Então, eh, no caso aqui, cada tábua de 540, ela vai gerar o quê? Ela vai gerar quatro novas tábuas. Só que eu já tinha 40 tábuas dela antes, né? Então eu vou ter aqui 160 tábuas. Vou somando aqui 160. Cada tábua original de 810, ela não vai gerar três tábuas de 270, ela vai gerar seis tábuas de
135, tá? Então eu vou fazer o quê? O 30 aqui xzes 6, que vai dar 180. Cada uma das tábuas de 1080 não vai gerar quatro tábuas de 270, ela vai gerar oito tábuas de 135. Então 10 x 8 vai dar 80, tá? Então 180 + 80, 260, 320, 420 tabas. Ou o dobro do que tu tinha antes, né? 420 peças. Letra E é a resposta. Beleza? OK. Sacou? Ã, é isso, tá? Então, bora. A última aqui hoje da da nossa aula. Com o objetivo de trabalhar a concentração e a sincronia de movimentos dos alunos
de uma de suas turmas, um professor de educação física dividiu essa turma em três grupos, A, B, C, e estipulou a seguinte atividade. Os alunos do grupo A vão bater palmas a cada 2 segundos. Os alunos do grupo B vão bater palmas a cada 3 segundos. E os alunos do grupo C vão bater palmas a cada 4 segundos. Pô, claramente aqui é um ciclo de palmas, né? Você a cada 2 segundos bate palmas. Então, bate palma, espera 2 segundos, bate palmas, espera 2 segundos. Aí o outro aluno do grupo Bate palma a cada 3 segundos.
Às vezes eles vão se encontrar. Por exemplo, entre os alunos do grupo A e B, qual é o MMC? Seis. De cara, porque os alunos do grupo A vão bater palma no segundo 2 4 6 e os do grupo B vão bater palma no segundo 3 e se vão se encontrar no seis. Mas e quando você bota o cara do do que vai bater de quatro em 4 segundos? Aí o MMC nesse caso vai ser o 12. Eles vão se encontrar no segundo 12. Os alunos que batem palma de dois em 2 segundos vão bater
2, 4, 6, 8, 10. 12. Os alunos que batem de 3 em 3 segundos vão bater 3, 6, 9, 12. E os que batem de 4 em 4 segundos vão bater 4, 8, 12. Legal. É tão fácil esse mmc que a gente faz de cabeça. Bacana. O professor zerou o cronômetro e os três grupos começaram a bater palmas quando ele registrou 1 segundo. Só que aí que tá, a questão é tão fácil, ela tem um mmc tão fácil que eles dificultaram para caramba em outro aspecto. Então essa questão aqui é mais difícil do que parece.
Já começa o seguinte, que o o professor não, eles não bateram a primeira palma juntos no segundo zero. Lembra que geralmente é assim, né? Geralmente no segundo zero começa a contar os remédios. os ciclos aqui não. Ele falou assim, ó, os alunos começaram a bater palmas, ou seja, os alunos bateram palmas juntos quando o professor botou um segundo. Então, quando o professor deu, quando bateu 1 segundo, os três tal, todo mundo bateu palma. E agora quando que eles vão bater de novo? Daqui a 12 segundos. A gente já sabe disso, daqui a 12 segundos, porque
12 é o MMC. Então agora a cada 12 eles batem palma. Ou seja, se os alunos bateram, só para deixar claro, né, galera, nem precisa aqui, não sei se eu preciso mostrar como fazer o mmc disso, né, mas eu vou mostrar só para mmc eu divido pelos fatores primos, né, independente de se todo mundo é ou não. Então aqui foi, aqui não foi, aqui foi. Boto dois de novo, aqui foi, aqui já tinha ido e aqui não foi. Agora boto o três, aqui foi. 2 x 2, 4 x 3, 12. A mmc é 12, tá?
Então, a primeira palma que eles vão bater, o professor disse, é no segundo um, ele falou, ele eles começaram a bater palmas no um segundo. Eles começaram, ou seja, eles bateram palmas ao mesmo tempo. Tau, tá? Beleza. E agora, quando que eles batem palma de novo? No 13 segundos. Se começa no um ou no zero, muda o resultado. Eh, o MMC sempre seria 12, mas se começassem no zero, aí eles iam bater palmas no segundo 12, no segundo 24, no segundo 36. E como começou no 1 segundo, eles batem palma no segundo 13. Agora vão
bater o quê? Com mais 12 segundos. Vão bater palma no segundo 25. Agora vão bater o quê? No segundo 37. Pegou? OK. Sim. Para quem tá perguntando, isso gera uma PA, tá? Para quem já já estudou PA lá no nosso nosso eh módulo matemática básica dois, tá? Ã, não é adicionar um segundo em cada ciclo, não. É você adicionar 12 segundos. Cada ciclo de em que eles batem palmas juntos acontece a cada 12 segundos, tá? Beleza? Não vai voltar aí de 12 em 12. Sempre tá indo de 12 em 12. É só que o professor
eles bateram palmas juntos pela primeira vez no segundo um. E aí, eh, o mmc é 12 quer dizer que a cada 12 segundos eles batem palmas juntos. Como eles começaram no um, isso vai acontecer no 13, no 25, no 37. Se eles tivessem começado a bater palmas no segundo três, eles iam bater juntos no segundo 15, com mais 12 segundos sempre, entendeu? Esse intervalo de 12 segundos para que eles batam palmas juntos, isso é sempre, é o mmc, ok? Todo mundo tá comigo? Entendido? Aí, tá. Então agora vamos vamos seguir aqui, né? Só confirmando aqui
se tá tudo certinho. Tá tudo certinho na gravação aqui. Então, então tá. Ó o que ele fala. Um estagiário notou no papel uma sequência formada pelos instantes em que os três grupos bateram palmas simultaneamente. Olha só, os instantes em que os três grupos bateram palmas precis e simultaneamente ao mesmo tempo. É exatamente o que eu anotei aqui. Eles bateram palma no um, eles bateram palma no 13, eles bateram palma no 25, eles bateram palma no 37 e assim vai. Bateram palma depois o quê? No 49. Somei mais 12. Depois bateram palma o quê? No 1
minuto e 1 segundo. Depois do 49, né? Você bota mais 12, vai dar 1 minuto e 1 segundo. Depois 1 minuto e 13 segundos e assim vai. OK, tá bom. Ã, e aí aí já tem gente ali falando, né? O moleque já falou assim: "Ah, tem que ver as alternativas então que engloba um segundo um, tá errado. Eu não vou ficar ensinando nenhuma dessas dessas coisas por enquanto de que ah, vamos então vamos testar as alternativas". Não, pô, pelo amor de Deus, não é para testar nada não, cara. É para você raciocinar e chegar na
resposta certa, tá bom? Não confunde, não. Eh, uma coisa é professor de YouTube, vai ficar, ah, tem que testar, vamos, vamos ver o macetinho para fazer aqui. Eu tô ensinando de verdade, entendeu? Aqui é para você aprender mesmo. Então, olha só o termo geral da sequência anotada, tá? Primeira coisa que termo geral é uma matéria de progressão aritmética, tá? Eu vou mostrar aqui como que se resolve com progressão aritmética, mesmo que eu ainda não tenha dado isso para essa turma agora, né? Porque progressão aritmética é só no módulo matemática básica dois e a gente tá
aqui no fundamento da matemática, tá? Mas vamos lá. Primeira coisa, sem progressão aritmética, ele quer saber uma uma fórmula que essa fórmula ela tenha a previsão de quando que os alunos vão bater palma juntos. Entendeu? Vamos entender. Isso aqui não é testar, isso aqui é entender, né? Vamos lá. 12n. A fórmula é 12n. Ah, tu quer saber quando que os alunos vão bater palma juntos? É 12n. Como assim 12n? É 12n, tá? 12n. Sendo que o n vai ser um número natural, que ele tem que ser maior ou igual a 1 e tem que ser
menor ou igual a 5. O que que isso quer dizer, né? 12n é literalmente 12 x n. Mas quem que seria esse N? Esse N seria ã a vez, esse N seria, seria a vez em que os alunos estão batendo palmas. Quando que eles estão batendo palmas juntos? Esse é o N, né? O número de vezes em que eles bateram palmas juntos. Então, vamos só visualizar como que isso poderia funcionar para vocês entenderem, porque e eu não dei isso ainda para vocês, mas só para vocês entenderem como que se raciocina uma equação, tá? 12n. Vamos
supor, a primeira vez que os alunos bateram palma, a primeira vez o n vai ser igual a 1. Você concorda? n = 1 na primeira vez que eles bateram palmas juntos. Certo? Vamos ver se dá certo. O que que é 12n? Quer dizer o quê? Multiplico o 12 pelo n. Só que o n aqui é um. Eu tô testando a primeira vez que os alunos bateram palmas juntos. Ah, eles bateram palmas juntos no segundo número 12. Já tá errado. Eles batem palmas juntos no segundo número um. Eles batem palmas juntos no segundo número 13. Eles
batem palmas juntos no segundo número 25. Entendeu? Deu para você visualizar, então isso aqui já não tá certo. Isso já não tá certo. Tá entendendo? Pegou? É claro. Ah, Pedro, você mostrou isso aí por teste. Não, mas é porque eu tô querendo te mostrar como que se pensa em equação. Mas você não pode aprender a fazer a questão por teste em si, tá? Eu tô querendo que você entenda. A opção aqui, ela tem que me dar uma equação, tem que dar me dar uma fórmula que preveja qual vai ser o momento em que o aluno
vai, os alunos vão bater palmas juntos. A primeira não, não funciona porque a primeira só diz assim, ó, 12n. Aí quer dizer, se eu quiser saber qual foi a segunda vez que eles bateram palmas juntos, ou seja, se eu quiser que o n seja 2, né? Coloca aí agora 12n, vai ficar 12 vezes o 2, que é o que é o n = 2 que eu defini, né? 24 segundos. Não, o moleque falou ali, Pedro, o moleque acabou de falar assim, não tem como fazer essa questão sem ser por teste, né? Claro que tem, tá
bom? Termo geral de uma PG é an, que é igual a 1 + n - 1 vezes a razão. A razão aqui no caso é o o a frequência, né? O período da frequência que é 12, beleza? An termo n que eu quero saber, um termo genérico, tá bom? Que vai ser expresso pelo primeiro termo, que é 1 segundo. E esse 1 segundo aqui somado aqui com n - 1 x 12. Beleza? Se você reescrever essa fórmula aqui, vai ficar que o termo geral é o quê? É 12 x n, né? que dá 12n men
12. Nem precisa fazer isso, né? Só você visualizar aqui no no já tá a resposta aqui, né? Eh, 12 que multiplica um parêntese com n - 1, tá aqui, ó. 12 que multiplica um parêntese com n - 1 + 1, tá aqui, só tá escrito aqui ao contrário, tá? É bem bem simples, inclusive, é porque você ainda não viu lá o matemática básica do n aulas de PA eu ensino isso aqui, tá bom? Então, dá sim para resolver, tá bom? Não é para resolver por teste, não. É mais rápido inclusive você resolver assim. É que
eu tô ensinando aqui a raciocinar. Então, vamos lá. ensinando aqui a raciocinar agora com com ferramentas básicas, tá? Sem usar a fórmula do termo geral. Sem usar a fórmula do termo geral. E detalhe, também dá para você raciocinar sem usar a fórmula do termo geral, mas usando conhecimentos de equação. Também dá, né? É só você tentar sintetizar matematicamente o que tá acontecendo aqui. Por exemplo, né? O aluno bateu palma aqui. Eh, vamos lá. A primeira vez que o aluno bateu palma foi no segundo um e a segunda vez que ele bateu palma foi no segundo
13. Aí você raciocinar o que que está acontecendo aqui para que isso para que isso aconteça, né? Então eu tenho sempre aqui a presença do tempo um. Eu tenho sempre a presença de um tempo um que ele vai ser somado sempre, sempre, sempre. Eu começo já tendo esse tempo um. Eu começo tendo um segundo no relógio. Então esse segundo um ele tem que ser somado. Mas e agora o que que acontece? Ah, eu adiciono mais 12 segundos. Eu adiciono mais 12 segundos. É verdade. Eu adiciono mais 12 segundos. Mas esses 12 segundos eles têm que
ser adicionados quantas vezes? Eles têm que ser adicionados o número de vezes do ciclo atual, por exemplo. Não, porque no ciclo um, o aluno só bateu palma vez. Essa é a primeira vez que ele bate palma. Se eu adicionar aqui agora o número um, que é o tempo que eu tenho aqui, e o e o número 12, que é o mmc, mas eu multiplicar o 12 pelo número de vezes do ciclo, isso dá errado. Isso dá errado. Na verdade, no primeiro momento, eu tenho que adicionar o 1 segundo. E o 12 tem que ser adicionado
quantas vezes? Nenhuma vez. Então, sabe quantas vezes o 12 tem que ser adicionado? O número de vezes do ciclo atual -1 para dar zero. Aqui no primeiro caso, o ciclo atual não é o ciclo 1. -1 dá o quê? Zero. Aí o 12 nem adicionado, fica só com um, que é a resposta. No primeiro, a primeira vez que eles batem palma é no segundo um. E no, e qual é a segunda vez que eles batem palma? Ou seja, aqui é a segunda vez, né? O n tem que ser igual a 2. Então, na segunda vez
que eles batem palma, eu já tenho o número um que vai ser somado aqui, que tá sempre presente. E eu faço o quê? Eu adiciono o número 12, que é o mmc. Mas quantas vezes eu vou botar esse número 12? Ah, vou botar o número 12, o número de vezes do ciclo. Não, porque se se o ciclo se já tem dois ciclos aqui, se já é a segunda vez, eu estaria botando 24 números aqui. Aí daria 25, não é isso, né? Na verdade, tem que botar o número 12, o quê? O número de vezes do
ciclo -1, que aí eu vouar no segundo ciclo -1. Isso dá 1. dá 12 + 1 dá 13. Entendeu? Sacou? Então é outra forma aí de você fazer. Agora, qual é a forma mais básica de você fazer isso aqui? Primeira coisa aqui para aprendizado é você saber analisar as alternativas, tá bom? O que que ele quer? Ele quer uma fórmula que que preveja isso. Ele quer uma fórmula que ela te dê a previsão de quando que os alunos vão bater palmas, sendo que n, ele tinha que ter dito isso, né? Mas ele nem disse, né?
Ele não falou isso, mas ele tinha que ter dito que n seria o o número de vezes, né? Em que o ciclo tá acontecendo. Qual é a vez em que o aluno tá batendo palma simultaneamente? Tá bom? Não faz sentido ser aqui o 24n também, né? Porque ã já não dá certo, né? A primeira vez que ele bate palma em 1 segundo, a segunda vez em 13 segundos. o 12 que multiplica o n - 1. Vamos ver se isso aqui funciona. Por exemplo, o segundo ciclo vai dar certo assim? Então aqui, ó, 12 xo ciclo,
aí pega n - 1. Então segundo ciclo - 1, fica só 12 x 1. Isso aqui dá 12, não dá 13. O que aí você já vê que o que que tá faltando aqui? O que tá faltando mesmo é somar um nisso. O que tá faltando é que tem que ter um nessa fórmula, né? E você vai chegar na letra D. A letra D é a resposta, tá bom? É o 12, que é o mmc, né? Que vai adicionando 12 segundos a cada vez. E esse 12 vai ser multiplicado pelo número de vezes que os
alunos bateram palmas simultaneamente, mas é esse número de vezes menos uma vez, tá? E mais o um, que já é o tempo que tá ali, tá bom? Então a resposta é letra D. Ã, e se você testar isso aqui, você vai ver que funciona, tá? Você vai colocar aqui 12 vezes, ã, vamos testar aqui pro segundo ciclo. Segundo ciclo n - 1, mas a letra n do segundo ciclo é 2, porque é o segundo ciclo -1 e isso mais 1 e isso mais 1. Então 12 que multiplica 2 - 1, que vai dar 1, né?
Dá 12 + 1, dá 13. Por que que isso aqui tá certo também, né? sendo que o n só pode ser no máximo cinco. O n tem que ser no máximo cinco. Ele pode ser menor ou igual a cinco. Porque quando o n vira 6, a gente já passa de 1 minuto. E aí não, aí muda o formato da resposta, né? Se o n aqui fosse 6, ia ficar o quê? 12 x 6 - 1 + 1. Então ia ficar 12 x 5 + 1, ia ficar aqui 61, tá? 60 + 1, 61 ia ser
e a resposta. Só que e aqui no caso teria que mudar a equação, né, para ela trazer o formato também em minutos. Beleza? É isso, tá? Então, eh, a resposta é letra D, sendo que ela só funciona até o NC5, tá bom? Então, aí mais uma questão de mmc, mas essa questão é bem mais avançada. Essa aqui é ele, o professor também para em 60 segundos, né? Tem isso. Ele tava dizendo aqui, né? O professor ele eh ele parou quando deu 60 segundos. Então, a fórmula nem precisa passar disso, tá? Então é isso, galera. É
uma questão mais avançada, é uma questão de progressão aritmética, é uma questão de equação, mas ela usa o conceito de mem, então por isso que eu trouxe pra gente resolver, tá bom? Então, galera, até a próxima aula, que é hoje às 4 horas, tá bom? aula de radiciação e um beijo aí para todos vocês. Parabéns por terem pronto, terminamos aqui. Eu espero que você tenha gostado, tá? Espero que tenha sido bom para você, né? Eu me esforcei aí para deixar tudo certinho, né? Então é um vídeo de 12 horas sobre toda a matemática básica, básica,
básica pro Enem, tá bom? É um vídeo para quem tem muita dificuldade. Espero que tenha ajudado. E se tiver aqui embaixo algum link com alguma promoção pra plataforma S, eu recomendo fortemente que você entre, porque isso aqui é só um pedacinho do pedacinho do que que a gente tem lá. Isso aqui não é nada perto do que a gente tem lá. lá realmente você tá dentro de um ecossistema em que eu dou todas as aulas. Então eu te explico tudo com uma didática muito absurda, mesmo que você esteja em nível muito baixo ou que esteja
em nível muito avançado, você sempre vai gostar, tá bom? Não esquece de curtir o vídeo, engajar, recomendar esse vídeo para as pessoas, comentar aqui o que que você achou. Gosto muito, leio todos, tá bom? Tudo que vocês falam, eu leio aqui, curto e é isso. Valeu, galera. Um beijo para todo mundo. Tchau tchau.
Related Videos

9:44:15
TUDO DE CITOLOGIA PARA O ENEM 2025 | DIDÁT...
Pedro Assaad | ENEM 2025
193,045 views

25:44
NÃO ERRE MAIS MATEMÁTICA! TODO CONCURSEIRO...
Professor Dê Ribeiro - Concursos
492,346 views

7:23:20
TUDO de FUNÇÃO do PRIMEIRO GRAU pro ENEM 2...
Pedro Assaad | ENEM 2025
165,226 views

10:50
Como DOMINAR a Matemática faltando 6 meses...
Lucas Tardin
14,728 views

5:34:11
🔴 Gabarito ENEM 2023 MATEMÁTICA: Todas as...
Matemática Rio com Prof. Rafael Procopio
58,135 views

4:00:37
4 Hours Chopin for Studying, Concentration...
HALIDONMUSIC
18,819,189 views
![Upbeat Lofi - Deep Focus & Energy for Work [R&B, Neo Soul, Lofi Hiphop]](https://img.youtube.com/vi/THh4fT0O7IY/mqdefault.jpg)
3:22:29
Upbeat Lofi - Deep Focus & Energy for Work...
A Lofi Soul
1,109,851 views

11:54:59
Jazz Relaxing Music ~ Cozy Coffee Shop Amb...
Relax Jazz Cafe
51,990 views

8:04:05
TUDO DE GEOGRAFIA FÍSICA PARA O ENEM 2025 ...
Pedro Assaad | ENEM 2025
166,648 views

3:15:53
Classical Music for Brain Power | Mozart, ...
HALIDONMUSIC
11,383,738 views

33:47
⚡️Атака России: коллапс в аэропортах Москв...
Ходорковский LIVE
81,140 views

5:23:18
TUDO de LOGARITMO pro ENEM 2025 (didática ...
Pedro Assaad | ENEM 2025
77,944 views

6:26:52
🏆 TUDO DE MATEMÁTICA PARA O ENEM 2024 (cu...
Umberto Mannarino
739,071 views

5:33:16
LEIS DE NEWTON - porém irá mudar a sua vida.
Pedro Assaad | ENEM 2025
21,220 views
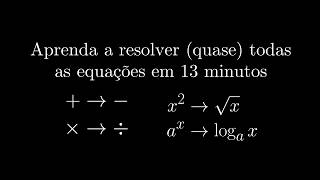
13:17
Como Resolver Qualquer Equação (ou quase t...
Principia Matemática
132,868 views

2:00:36
Intense Study - 40Hz Gamma Binaural Beats ...
Study Sonic Focus
7,860,950 views

2:58:18
📗 Rumo à Medicina: Estude Comigo para o E...
Dr. Renato Palmeira | ENEM 2025
6,289 views

5:52:36
TUDO de QUÍMICA GERAL pro ENEM 2025 (GANHE...
Pedro Assaad | ENEM 2025
103,445 views

5:31:56
REVISÃO de MATEMÁTICA para o ENEM (ENEM 2023)
Vinícius Oliveira
34,019 views