O que são Coordenadas Esféricas: Visualização e esboço de sólidos | Integrais Triplas

O que são as coordenadas esféricas e como a gente trabalha com elas vamos lá entender Oi gente meu nome é Ester Velasques e sejam bem-vindos a mais um vídeo do canal matemateca nessa aula a gente vai começar a falar sobre coordenadas esféricas entendendo cada um dos parâmetros como funciona e como a gente vai aplicar isso lá nas integrais triplas Tá bom então antes de começar Já curte aí embaixo se inscreve no canal e vamos lá gente vamos começar dando uma revisada nos tipos de coordenadas que a gente já viu a gente já falou sobre coordenadas

polares que é quando a gente troca a coordenada x y a gente troca o idioma desse ponto para um outro idioma cujos parâmetros São R e tétano então aqui a gente consegue escrever um ponto que seria visto como algum x e algum y e ao invés de ser visto com essas coordenadas ele vai ser visto com as coordenadas r e tétano onde R é a distância desse ponto até a origem e o teta é o ângulo que é formado entre esse segmento aqui que liga o ponto é a origem e o eixo X o eixo

horizontal Então as coordenadas polares permitem que a gente represente um ponto em um novo idioma no idioma r e tétano a gente viu também sobre as coordenadas cilíndricas que são bem com as coordenadas polares só que aí a gente vai para três dimensões aqui também a gente vai ter o r e o teta mas nesse novo idioma a gente acrescenta um parâmetro que é o parâmetro Z então nas coordenadas cilíndricas a gente tinha R teta e z o r é a distância do ponto até o eixo Z Então até o eixo Z como um todo

né Então essa distância aqui que tá Projetada aqui embaixo o teta permanece sendo o ângulo Entre esses segmento e o eixo X então Teta vai variar aqui no chão né aqui embaixo e o z é a altura que o nosso ponto tá em relação ao eixo Z então se ele tá aqui no três se ele tá no cinco se ele tá no menos dois Então dependendo de onde o ponto tá a gente vai alterando a terceira coordenada que a coordenada Z então o ponto visto em coordenadas cilíndricas R teta Z agora a gente vai ver

um novo tipo de um novo idioma aqui que a gente pode migrar os nossos pontos que são as coordenadas esféricas Então as coordenadas esféricas também vão servir para representar pontos em três dimensões então transferir esse ponto X Y Z para um novo idioma só que esse idioma é diferente do idioma que das coordenadas cilíndricas aqui o idioma era R teta e z né agora a gente vai para outro país aqui que fala outro idioma e os parâmetros agora vão ser roteta e fim vão ser os nossos três parâmetros para representar um ponto aqui no espaço

então assim como cada parâmetro tinha suas funções aqui nas coordenadas polares nas cilíndricas a que cada parâmetro também Vai representar alguma coisa em particular que vai deixar cada pontinho aqui do espaço ter a sua singularidade de acordo com esses três parâmetros Então vamos lá entender como vai funcionar para começar o parâmetro home ele vai representar a distância do seu pontinho até a origem então o Quão distante o seu ponto tá da origem então diferente do parâmetro R que a gente tinha aqui atrás ele não vai ser a distância necessariamente até o eixo Z ele é

a distância do ponto até a origem até o 000 Então essa distância aqui vai ser nossa primeira coordenada coordenada How A segunda coordenada que é o teta permanece sendo o mesmo teta que a gente estava acostumado é o ângulo Entre esses segmento que e o eixo X então ó Aqui é onde ficava o r né quando a gente trabalhava com coordenadas cilíndricas o r não tá mais por aqui mas o teto permanece ele continua sendo o ângulo Entre esses segmento e o eixo X e por fim o nosso novo amigo aqui vai ser o fim

ele é o ângulo formado entre esse segmento aqui também e a parte positiva do eixo Z então essa parte aqui então aqui a gente tem o eixo x y e z e como funciona cada um desses parâmetros nas coordenadas cilíndricas aqui a gente tinha R aqui a gente tinha Z e aqui a gente tinha teta né agora a gente tem o roo aqui é uma distância até a origem ao invés de ser até o eixo Z o teta permanece sendo a mesma coisa e o fim é o ângulo entre esse segmento do rô e o

eixo Z é importante a gente reparar primeiramente que o Rô sempre vai ser um valor positivo porque a gente não tem distância negativa né a gente não tem como falar que a distância entre esse ponto e a origem é menos dois não a distância é o tamanho disso aqui ó é esse tamanho aqui então continua sendo algo positivo então se você tem um ponto aqui sua distância até a origem é o tamanho desse se todo o teta ele pode variar entre 0 e 2 pi ou seja ele pode dar a volta completa aqui no chão

ó lá para trás tem o resto do eixo X né o teto ele pode fazer tudo isso aqui toda essa volta completa porque o nosso ponto pode estar aqui pode estar lá atrás pode estar aqui pode estar aqui na frente então o ângulo formado com eixo X como um todo pode variar a volta inteira agora o fim que é o ângulo com a parte positiva do eixo Z como a gente só tá considerando a parte positiva só essa parte aqui de cima o nosso ângulo só pode variar entre 0 e pi porque olha só zero

é quando o nosso ponto tá em cima do eixo Z o ângulo dele com eixo Z com a parte positiva do eixo Z né É zero e aí pi vai ser quando o seu ponto estiver aqui na parte negativa do eixo Z Então você andou meia volta pi radianos agora se o ponto tiver mais para cá ó se ele estiver nessa região aí o ângulo com a parte positiva do eixo Z começa a contar aqui do outro lado então esse ângulo com a parte positiva do eixo Z só varia entre 0 e pi ou para

esse lado ou para esse aqui mas está sempre Entre esses valores já que a gente está falando só da parte positiva a gente então uma visualização gráfica aqui de como funciona as coordenadas esféricas o Rô vai dizer respeito à distância do nosso ponto até a origem então quanto maior o Rô mais distante a gente tá da origem que por exemplo o teta ele fala sobre o nosso ângulo com o eixo X esse eixo vermelho aqui ó aqui a gente tá formando um ângulo de 0 graus 0 radianos com eixo X então são os pontos que

estão aqui na altura do eixo X né da parte positiva dele aí conforme o ponto vai indo para outros quadrantes Ó aqui tá o nosso ponto P esse ângulo com eixo X vai aumentando ó aqui é o ângulo de 180 graus quando a gente deu meia volta X então o ângulo Teta vai dizer a respeito à localização do nosso ponto em relação a qual o octante ele tá se ele tá nesse aqui se ele veio para esse aqui se ele veio para esse ou para esse então de acordo com o lugar que o nosso ponto

tá esse ângulo vai variando e por fim o ângulo Fi vai dizer se o nosso ponto está para cima ou para baixo porque ele diz respeito ao ângulo com a parte positiva do eixo Z Então se o fio for maior do que pi sobre dois a gente vem aqui para baixo se ele for menor do que pi sobre dois a gente tá aqui na parte de cima então a gente pode variando esses parâmetros e obtendo diferentes pontos aqui no espaço então a gente está representando um ponto que poderia ser representado com x y z só

que ao invés de isso a gente tá representando com o teta e fim mas agora fica a pergunta como a gente converte um ponto x y z algo que tá nas coordenadas que a gente tá acostuma do né as coordenadas retangulares como a gente converte isso para as coordenadas esféricas Rô teta e fim ó vamos pensar o seguinte quem é o x aqui o X é essa coordenada aqui do nosso ponto né É onde nosso ponto tá localizado em relação ao eixo X olhando que geometricamente E lembrando que isso aqui era o r lá no

nas coordenadas cilíndricas a gente pode observar que aqui ó entre XR e y a Gente Tá formando um triângulo retângulo então ó a gente tem um ângulo teta aqui e o X é o cateto a adjacente a ele então a gente pode escrever que o cosseno de teta é igual o cateto adjacente que é x sobre a hipotenusa que é R ou seja X = R vezes cosseno de teta mas isso a gente usava lá em coordenadas cilíndricas né vamos transferir aqui porque o r não faz parte das coordenadas esféricas então olhando que para o

outro triângulo que a gente tem formado é outro triângulo retângulo formado aqui o r agora é cateto oposto ao ângulo Fir ó Lembrando que esse ângulo aqui é igual a esse né então a gente pode escrever que o seno de fi é igual o cateto oposto que é R sobre a hipotenusa que nesse triângulo aqui é Rô ou seja R = vezes seno de fi Isso aqui é uma verdade por causa desse segundo triângulo aqui que a gente tá vendo em verde então o x é igual R que errou vezes seno de fi vezes o

cosseno de teta Então essa é a expressão para a gente encontrar o x a gente a gente vai comprovar que cada uma delas para você entender direitinho tá bom Agora vamos encontrar quem é o y em função de Rô teta e fim então o y aqui nesse de baixo ele é o cateto oposto ao ângulo teta então a gente pode escrever que o seno de teta é igual o cateto oposto a ele que é y sobre a hipotenusa que é R então y é igual R só que o r errou vezes o seno de Fi

né E isso tudo multiplica o seno de teta aqui então essa é a expressão para encontrar o y em função de roteta e fim e por fim vamos encontrar o z o z é o cateto adjacente ao Fi aqui nesse triângulo retângulo que está em pé então a gente pode escrever que o cosseno de fi é o cateto adjacente a ele sobre a hipotenusa que nesse triângulo retângulo aqui é o home ou seja Z é igual ro vezes cosseno de fi é assim que a gente representa o z em coordenadas esféricas então resumindo quando a

gente quer converter X Y Z para rotetas a gente vai usar essas relações que a gente acabou de comprovar o x erro vezes seno de fi vezes cosseno de teta o y errou vezes cada um dos senos o seno de cada um dos ângulos né e o z errou vezes cosseno de Fi agora se você já tiver o teto e o fim e você quiser voltar para o outro idioma para o idioma das coordenadas retangulares você pode usar Que roupa ao quadrado é igual x ao quadrado mais y ao quadrado Mas é ao quadrado ro

é igual a distância entre o ponto x e y z e a origem né e a fórmula de distância entre um ponto e a origem é dado por essa expressão por isso ao quadrado é x² + y² mas é ao quadrado e usando essa relação aqui você pode essas que a gente viu aqui atrás também para converter rotath para x y e z Então vamos lá fazer alguns exercícios sobre isso gente primeiramente a gente quer encontrar as coordenadas retangulares de um ponto que as coordenadas esféricas deles são dadas dessa forma ó quatro pi sobre 3

e pi sobre 4 então aqui a gente já tem as coordenadas esféricas olha ele falou que possui essas coordenadas esféricas e a gente quer encontrar as coordenadas retangulares a gente quer encontrar quem é x y e z que representa esse pontinho aqui então nesse ponto como ele já tá nas coordenadas esféricas a gente tem que o quatro é o nosso Rô o pi sobre 3 é o nosso theta e o pi sobre 4 é o nosso fim então é sempre essa ordem gente teta e fim então sabendo esses três parâmetros a gente consegue encontrar Quais

são os parâmetros x y e z que representam esse ponto então começando pelo X o X é ro nosso roo aqui no caso é quatro vezes o seno de Fi aqui no nosso caso o fi essa terceira coordenada né pi sobre 4 então seno de pi sobre 4 vezes o cosseno de teta o nosso teto aqui é pi sobre 3 Então a gente tem quatro vezes o seno de pi sobre 4 é o seno de 45 graus é raiz de 2 sobre 2 o cosseno de pi sobre 3 que é o cosseno de 60 graus

é um sobre dois então a gente pode cortar o 4 com 2 x 2 aqui embaixo e a gente encontra aqui o X é raiz quadrada de dois agora o ele vai ser ro vezes o seno de cada um dos ângulos então vezes o seno de pi sobre 4 vezes o seno de pi sobre 3 Então a gente tem quatro vezes raiz de 2 sobre 2 que é o seno de pi sobre 4 vezes raiz de 3 sobre 2 que é o seno de pi sobre 3 o seno de 60 graus então mais uma vez

a gente corta o 4 com 2 x 2 e vai sobrar para gente raiz de 2 vezes raiz de 3 que é a mesma coisa que √6 e por fim o z errou vezes o cosseno de fio então vezes o cosseno de pi sobre 4 então a gente tem quatro vezes raiz de 2 sobre 2 que vai dar 2 raiz de 2 então encontramos o x e o z esse mesmo ponto aqui só que nas coordenadas que a gente tá acostumado vai ser o ponto raiz de 2 raiz de 6 2 raiz de 2 esse

é o ponto nas coordenadas x y e z então gente lembrando as duas coisas estão representando o mesmo Ponto só que em idiomas diferentes Então a gente tem exatamente o mesmo ponto ali no espaço a diferença é que aqui nas coordenadas esféricas ele tá representando assim ó a distância entre esse ponto é a origem Vale 4 a o ângulo que formado com eixo X é pi sobre 3 e o ângulo formado com a parte positiva do eixo Z é pi sobre 4 enquanto no x y z que a gente está mais acostumado ele tá falando

ó no eixo X Ele tá na altura √2 no eixo Y ele tá na altura √6 e no eixo Z ele tá na altura 2 raiz de 2 E aí pegando essas três alturas você encontra Onde está seu ponto gente agora nesse exercício a gente já tem as coordenadas retangulares e a gente quer encontrar esse mesmo Ponto escrito em outro idioma nas coordenadas esféricas então para começar quando você já tem o x y e z o ponto x y z você quer encontrar o ponto rota teta e fim você vai lembrar que ao quadrado é

igual x ao quadrado mais y ao quadrado mais Z ao quadrado então o primeiro passo que você vai seguir é encontrar o Rô então ao quadrado é igual um mais um mais dois que dá quatro portanto é igual a raiz quadrada de 4 que vale 2 já encontramos a distância do nosso ponto até a origem agora que a gente tem o home o segundo passo é a gente encontrar quem é o fim para isso a gente vai lembrar que o z é ro vezes cosseno de fi isso ajuda a gente porque a gente já tem

o z foi dado que no ponto né E a gente já tem o Rô que a gente encontrou pela relação do quadrado Então é só substituir aqui para encontrar o fim então a gente tem que ver que é raiz de 2 = vezes cosseno de fi Portanto o cosseno de fi é igual raiz de 2 sobre 2 logo a gente encontra aqui Fi é pi sobre 4 radianos é o ângulo cujo cosseno Vale raiz de 2 sobre 2 Então agora que a gente tem o Rô agora que a gente tem o fim a gente pode

encontrar o teta para isso você pode usar ou a equação do Y ou a equação do X a equação do Y fala que é igual ro vezes o seno de teta vezes o seno de fi Mas você também pode usar do X se você preferir Tá bom então o nosso Y Vale 1 o nosso Rô vale 2 o seno de teta é a nossa incógnita e o seno de fi vai ser o seno de pi sobre 4 que vale raiz de 2 sobre 2 então a gente pode cortar aqui o dois de cima com dois

de baixo e sobra que raiz de 2 vezes o seno de teta é igual a 1 logo o seno de teta vai ser um sobre raiz de 2 e se você multiplicar por raiz de 2 em cima embaixo racionalizar Isso Aqui você encontra raiz de 2 sobre 2 ou seja o teta é o arco cujo o seno então um arco seno de raiz de 2 sobre 2 Então quem é o ângulo que o seno Vale raiz de 2 sobre 2 e sobre quatro também né gente então pi sobre 4 tantos seno quanto cosseno dele valem

√2/2 Então esse mesmo Ponto que representado em outro idioma em coordenadas esféricas vai ser o Rô que vale 2 o teta que vale pi sobre 4 e o fi também vale pi sobre 4 agora olha esse exercício aqui gente a equação de uma esfera centrada na origem e com raio c é dada dessa forma aqui então essa equação está representando uma esfera com raio C como fica a equação dessa esfera então a equação desse superfície que a gente tem em coordenadas esféricas como a gente migra isso para coordenadas esféricas então bom a gente sabe que

x² + y² + B ao quadrado é a mesma coisa que Rô ao quadrado não é bom a gente quer sair do x y e z imigrar para algo que tenha [Música] algo que seja escrito nesses parâmetros e para começar a gente já sabe que x² + y² + b² é o próprio Rô ao quadrado né então a gente tem que ao quadrado é igual C ao quadrado você é uma constante não precisa a gente se preocupar com ele ele é o raio da esfera mas se ao quadrado é igual ao C ao quadrado A

gente encontra que errou é igual a c certo ou seja a equação de uma esfera em coordenadas esféricas é a mais simples que a gente pode ter ela tá simplesmente falando ó é igual o raio da esfera então distância de qualquer ponto da esfera até a origem sempre vale ser e de Fato né quando você tem uma esfera não importa o ângulo com eixo X o ângulo com eixo Z eles podem variar o quanto eles quiserem a única coisa que importa na Esfera é que a distância de todos os pontos dela até a origem sempre

é igual o raio dela gente para ter acesso a essa em muitas outras aulas e exercícios resolvidos das matérias do seu curso vem fazer parte da plataforma matemática Academy lá você tem acesso a aulas exercícios resolvidos provas antigas resolvidas e uma comunidade onde você pode tirar suas dúvidas e conversar com outros alunos que estão cursando as mesmas matérias então se você tiver interesse é só clicar no link da descrição matemática.com para conhecer as nossas opções de planos Tá bom então vamos lá agora olha esse exercício aqui gente a gente quer esboçar o sólido aqui no

espaço tem um x y z a gente quer esboçar o sólido que é descrito por essas desigualdades então ó a gente tem os parâmetros roteto e fim né E ele fala que o Rô é menor ou igual a 2 o teta tá entre 0 e pi sobre 2 e o fi também tá entre 0 e pi sobre 2 então ele falar para gente que o teta tá entre zero e pi sobre 2 A gente já sabe que a gente só vai estar nessa primeira parte aqui ó nesse primeiro quadrante aqui da frente a gente não

pode estar nesse quadrante aqui porque aqui a gente tem ângulos maiores do que pi sobre dois menores do que pi a gente não pode estar nesse outro quadrante aqui de trás porque aqui a gente tá entre pi e três pi sobre dois e a gente não pode estar nesse quadrante aqui porque aqui a gente tá entre três pi sobre dois e dois pi então é como visualizar o círculo trigonométrico olhando aqui de cima gente o teto varia exatamente igual ao círculo trigonométrico então se ele tá entre 0 e pi sobre 2 Ele só pode estar

nesse primeiro quadrante aqui a gente já sabe que o nosso sólido vai estar aqui agora ele também fala que o fim varia entre 0 e pi sobre 2 ele tá vindo desde o zero quando tá em cima da parte positiva do eixo Z e ele vai dar um quarto de uma volta ele vai até pi sobre dois também ou seja a gente nunca vai para parte negativa do eixo Z porque quando a gente vai para parte negativa a gente ultrapassa o ângulo de pi sobre dois a gente vem para ângulos entre pi sobre dois e

pi né ou quando a gente vem tudo aqui para baixo a gente dá meia volta que é o ângulo pi Então se a gente tá só entre zero e pi sobre dois a gente só deu essa parte aqui a gente veio só até o ângulo de 90 graus com a positiva do eixo Z o nosso sólido Além de estar aqui na frente ele também tá na parte de cima ele não vem aqui para parte de baixo o teta varia nessa região e o fi faz a gente variar nessa região agora a única coisa que falta

é ver até quando eles variam eles variam até 100 aqui até 200 como que funciona aí que a gente tem que olhar para o Rô o nosso roo só envolve valores menores do que dois então a nossa distância até a origem é no máximo dois aqui a gente vem até dois aqui até dois e aqui até dois a gente tá pegando um quarto de uma esfera gente ó lembra que a esfera completa englobava todos os valores de teto e o nosso único parâmetro seria o home aqui o teto e o fim resolveram se revelar eles

quiseram ter algum parâmetro ali e isso fez com que a gente pegasse apenas um quarto da nossa esfera Então essa é a figura que é representada por essas desigualdades agora vamos ver um outro caso desse para fechar aqui a gente tem que o Rô tá variando entre 2 e 3 e o fi varia entre pi sobre 2 e pi Então olha só como o teta não apareceu é igual acontecia aqui na equação da esfera o teta e o Ronan apareciam porque eles podiam assumir o que eles quisessem ali tanto faz a mesma coisa aqui como

tétano apareceu a gente vai considerar que o nosso sólido pode rodar aqui o quanto ele quiser ao redor do eixo X então a gente pode dar uma volta completa ao redor do eixo X agora o nosso fim só varia entre pi sobre dois e pi ou seja nosso ângulo com a parte positiva do eixo Z começa em pi sobre dois então começa aqui no ângulo de 90 graus e vai até uma volta uma volta é quando a gente está aqui na parte negativa do eixo Z e vai até meia volta né então aqui é pi

sobre dois aqui é até chegar no pi se ele tá indo de pi sobre dois até pi ele começa aqui no chão quando o ângulo é pi sobre dois e ele vem até a parte negativa do eixo Z embora o nosso sólido possa dar a volta completa ao redor do eixo X Ele só vai estar aqui na parte de baixo na parte negativa do eixo Z Então não vai ter sólido aqui para cima só para baixo Então até o momento o que a gente tem é uma esfera ou teta tá dando a volta completa né

então a gente pode andar tudo isso aqui que a gente tá pegando só a parte de baixo dessa esfera A gente não tá pegando a parte de cima porque a gente está limitando o ângulo com a parte positiva do eixo Z a gente tá pegando só a parte de baixo aqui mas agora o Rô ainda pode mudar essa história Qual é o raio dessa esfera até onde a gente tá indo aqui na superfície dela o Rô falou pra gente que a distância até a origem pode variar entre dois e três ou seja ao invés de

pegar todos os valores aqui que são menores do que três ou menores do que dois a gente vai dar mais uma limitada aqui para essa distância só variar entre dois e três então aqui é quando a distância é dois a parte interna aqui da nossa esfera né E aqui na parte de fora é quando a distância Vale três Então se fosse simplesmente Rô menor ou igual a 3 A gente ia pegar tudo isso aqui dentro do trem se fosse Roma menor igual a dois ia tirar essa parte de fora que essa casca de Fora ia

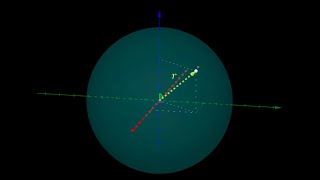
pegar tudo menor igual a dois mas como errou entre dois e três a gente tá pegando Exatamente Essa casca aqui da nossa esfera né a gente tá pegando Exatamente Essa superfície como se fosse um coco aqui então esse é o sólido que é descrito por essas desigualdades aqui a gente vamos analisar aqui como funciona cada um dos parâmetros quando a gente está falando de um sólido então se eu colocar o teta em 360 Graus o fim em 180 graus e colocar o Rô como três ó aqui o Ro tá valendo três a gente tem uma

esfera completa de raio igual a três ó a gente deu a volta completa ao redor do eixo X que é o eixo vermelho e a meia volta ao redor do eixo Z a gente tem essa esfera agora se eu te falar na verdade o home ele só vai até 90 graus que é o nosso pi sobre dois nesse caso ó tá variando entre zero 90 graus que é zero e pi sobre 2 e portanto a gente tá pegando só a parte de cima parte positiva do eixo Z Ah e se a gente tivesse pegando entre

45 e 90 graus aí a gente estaria pegando apenas os pontos cujo o ângulo com a parte positiva do eixo Z estão entre 45 graus e 90 graus Então esse sólido Aqui tá englobando todos os pontos cuja distância até a origem Vale três o ângulo com eixo X está variando entre 0 e 370 graus então dá essa volta completa aqui e o ângulo com a parte positiva do eixo Z varia entre 45 e 90 graus então ó a gente tá pegando desde 45 começa aqui os pontos que estão nesse cone aqui formam 45 graus com

eixo Z e a gente vai indo englobando até os que formam 90 e se eu for até 132 graus você vai pegar até os pontos que formam um ângulo de 132 graus com a parte positiva do eixo Z aí se eu pegar aqui o meu tétano e eu colocar ele para variar só entre 0 e 180 graus também então tá aqui por volta de 180 graus aí a gente vai dar só meia volta ao redor do eixo X então a gente começa aqui no zero quando o ângulo com eixo X Vale 0 e vai indo

até dar meia volta ao redor do eixo X ah e quero aumentar quero que o FIFA até 180 se você for até 180 ele vai a volta completa lá para baixo Então os ângulos entre 45 graus e 180 com eixo Z então gente o sólido que a gente forma tá englobando todos os pontos que comprem esses requisitos ó se a gente aumentar o Rô vai aumentar a distância desses pontos até a origem então a esfera vai ficando maiorzona né se diminuir a esfera vai ficando pequenininha se deixar o teto englobar menos ângulos a gente vai

dar uma volta menor ao redor do eixo X e assim vai variando então foi isso que a gente fez nesses últimos exercícios um sólido escrito por desigualdades vai englobar todos os pontos que cumprem aquilo ali que cumpre o ângulo externo entre tal e tal o Rô está entre 2 e 3 por exemplo ou então nesse último caso que a gente viu nesse último exercício o teta podia variar em qualquer valor né então a gente podia dar a volta completa ao redor do eixo X se ele tava variando entre pi sobre dois que é 90 graus

Vamos colocar aqui 90 graus e 180 então ele tava pegando só a parte de baixo e o Rô ele tava variando entre dois o rumo aqui é dois e o três vamos achar o três aqui ó então ele tava variando entre dois e três ó aqui esse a gente pegasse só o dois a gente pegasse só a esfera de Raio 2 aí conforme a gente vai aumentando a gente tá pegando mais pontos os pontos que a distância até a origem estão entre dois e três são os pontos englobados aqui dentro e por isso esse foi

o sólido que a gente encontrou o coco né para esse último exercício bom gente então foi esse no vídeo de hoje eu espero que vocês tenham gostado não esquece de curtir se inscreve no canal compartilha com seus amigos e já me segue lá no Instagram para ficar por dentro de tudo Tá bom então a gente se vê no próximo vídeo gente beijo [Música]