ÂNGULO CENTRAL E INSCRITO | ÂNGULOS NA CIRCUNFERÊNCIA |

o Natal aula você vai aprender sobre ângulos na circunferência Então veja que você vai aprender ângulo central e ângulo inscrito estão começando aqui com o ângulo central e ângulo central de uma circunferência é qualquer ângulo cujo vértice é o centro da circunferência então se você observar aqui o ângulo que eu trouxe desenhado eu tenho então um ângulo aob tá bom tá indicado aqui e você consegue observar que o vértice dele é bem no centro da circunferência então dá outra vez que acontecer isso nós teremos um ângulo central e lembrando uma coisa gente como é que

eu estou me referindo a um ângulo um ângulo ele é formado por semi-retas logo eu tenho que fazer o prolongamento você ficar aqui vai ficar com segmento né fazer direitinho aí profissão tudo bem E aí outra coisa que você deve saber também é sobre o arco arco AB então a AB então é tudo isso daqui ó o arco como se fosse eu peguei a uma fatia da Pizza penso na bordinha da pizza então o arco AB é o conjunto de todos os pontos da circunferência ó se eu pegar então todos os pontos aqui da circunferência

que vai de A até B inclusive ver deixa eu terminar de Lenny que pertence ao interior do ângulo aob Inclusive a e b que foi o que eu acabei de dizer para você então Aqui nós temos o arco AB a Jesus Mas tá bom e aí o que que tem de relação tem conta para fazer gente então é o seguinte quando você tem tem marcou aqui ó vídeo sobre falar para você o ângulo central e sobre o arco ao ver que daqui a pouco eu falo do ângulo inscrito é você marcou então sobre o ângulo

central e o arco Qual é a relação que nós temos entre o ângulo central e o arco ele tem a mesma medida porque a gente uma coisa aqui é de quem esse ângulo por Alpha mas veja que se eu marcasse aquele mesmo ângulo um pouquinho aqui para trás ou por exemplo ele não teria mesma medida teria porque a origem é a mesma se eu marcasse esse ângulo aqui por exemplo não queria mesma medida Siri porque a origem é a mesma é a mesma abertura se eu marcasse aqui onde está o arco não é a mesma

medida então gente Toda vez que você tiver um ângulo central e um arco a medida deles são iguais por exemplo se esse ângulo aqui Central que eu marquei de início fosse 80 graus a medida do arco também seria 80 graus certo então se por exemplo eu marcasse que o ângulo Alfa fosse de 80 graus então eu iria concluir que o que o arco AB também interia 80 graus se fosse a 50 aqui o arco seria 50 sempre a mesma medida e aqui se você quiser escrever no lugar de Alpha quiser escrever que é o ângulo

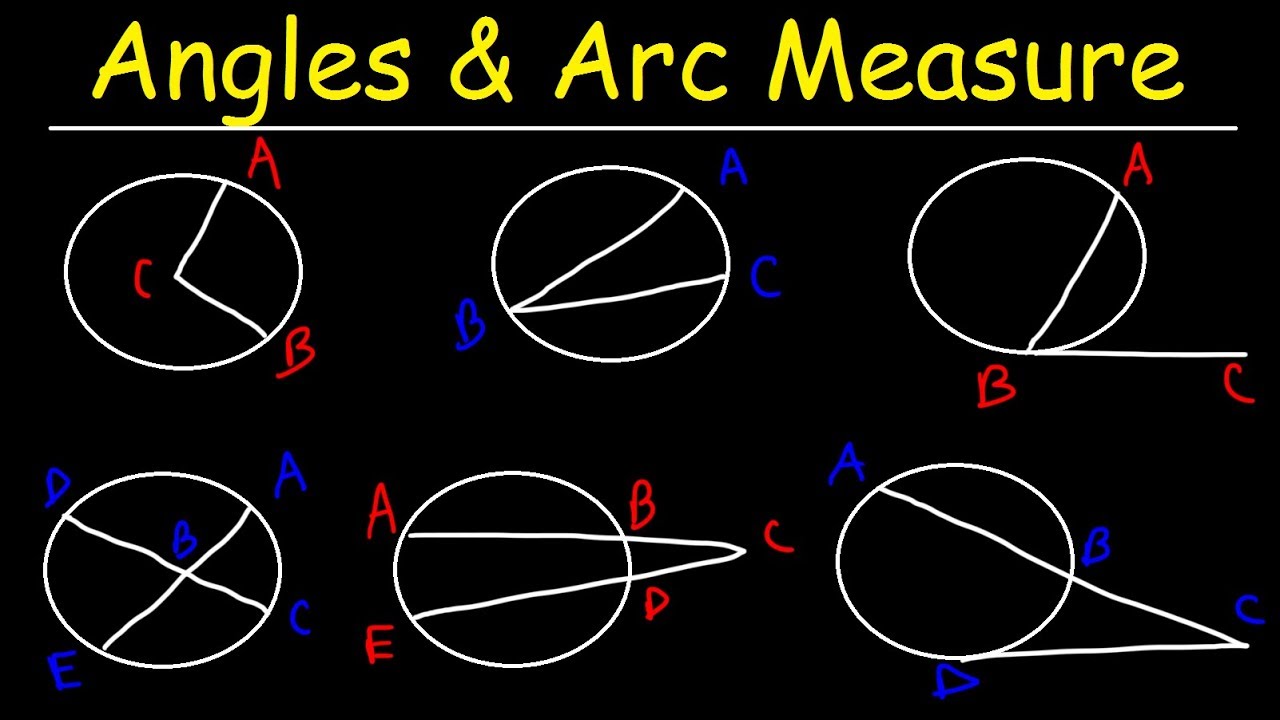
aop Você pode escrever também certo e agora nós vamos falar do ângulo inscrito que será que a diferença do ângulo central para o ângulo inscrito você tem ideia gente e agora um ângulo inscrito um ângulo inscrito em uma circunferência é qualquer ângulo cujo vértice agora não tá no centro mais tá agora o vértice pertence a essa circunferência e seus lados sejam secantes a ela ter secante quer dizer que eles passam por dois pontos e aí você pode observar que nesse caso diferente lá do ângulo central que o verbo estava no centro aquele tá em cima

da circunferência olha aqui ó um caso aqui tem um exemplo aqui eu tenho outro exemplo de é inscrito o verso está em cima da circunferência aqui também tem um outro caso o vértice tá em cima da circunferência e os lados são secantes né gente e aí diz qual que é a relação que nós temos quando for fazer os exercícios do ângulo inscrito veja que todo o ângulo escrito gente a medida desse ângulo inscrito ela vai ser igual à metade da medida do arco correspondente então por exemplo se eu tiver Deixa eu fazer de outra cor

se eu tiver por exemplo esse arco AB aqui ó o esse arco AB é rei ali né medindo por exemplo 120 graus aproximadamente qual vai ser a medida do meu ângulo inscrito você tem ideia falei o que que era igual à metade do seu arco correspondente Então quer dizer que esse ângulo inscrito e ele vai ser que metade vai ser 60° Ah e outra coisa que você pode observar se eu tivesse desenhado o ângulo central aqui ele teria mesma medida do arco você marca outra observação que eu falei já né E aí o ângulo inscrito

sempre a metade por exemplo aqui se eu pegar vou ver se eu acerto o desenho agora ó se eu pegar esse arco aqui ó o ou agora acho que foi em e eu falar que esse arco tem 80 graus gente só tô olhando a representação Tá qual vai ser a medida do ângulo inscrito vai ser a metade Então esse ângulo inscrito terá 40 graus e aqui nesse outro caso por exemplo se esse arco aqui a vale48 por exemplo a medida do ângulo que vai ser a metade 24 esse foram número ímpar gente por exemplo a

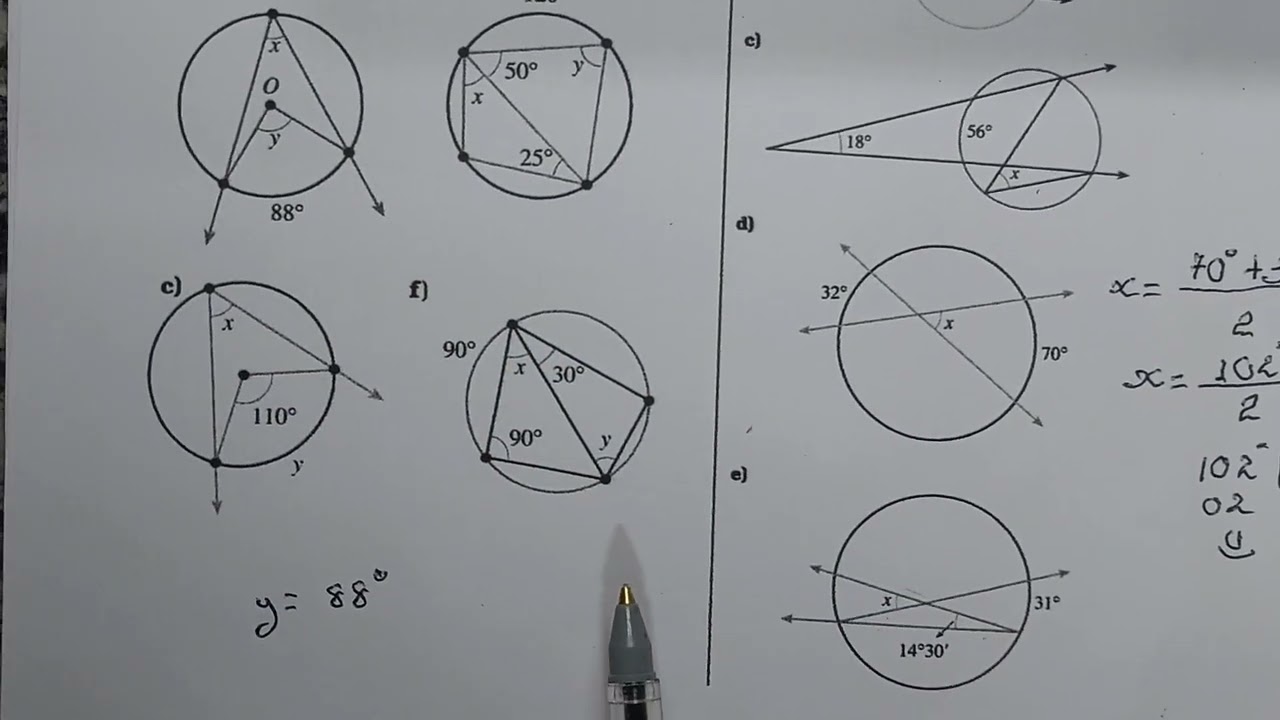
45 aqui seria 4522 e meio né 22 e meia a metade você pode trabalhar também com o meu impor Sem problema tá bom e agora nós vamos fazer exercícios Vamos lá gente agora não exercício olha ali você termine o valor de X em cada caso apresentado Então você já marcou né recapitulando quando eu tenho um ângulo central o ângulo central tem a mesma medida do arco certo do seu arco correspondente e quando eu tenho um ângulo inscrito com aquele ângulo que tem um vértice em cima da circunferência a medida desse ângulo inscrito é a metade

do arco correspondente ou também podemos falar que a metade do ângulo central que a né que a medida do arco igual ao ângulo central então a medida do inscrito é a metade do Central Tudo bem então vamos lá ver aqui nesse primeiro caso veja que eu tenho 140 aqui e fiz aqui quando que eu tenho mesmo ângulo central quando o Vert já está no centro então aqui é ângulo central e esse daqui como vértice está em cima da circunferência ele é um ângulo inscrito então o ângulo inscrito é a metade do ângulo central nossas mas

você não falou que o ângulo escrita metade do arco correspondente veja bem gente se eu desenhar o arco aqui ó que vem daqui ó o arco tá aqui no tal como vai seu acerto agora o desenho Tá aqui ó o arco tá aqui se o ângulo central Vale 140 Quanto que mede esse arco não é 140 também então só se eu já tenho a medida do ângulo central posso fazer a conta com ele se o ângulo central é 140 um ângulo inscrito vai ser a metade então quer dizer aqui gente que a medida do X

que é o ângulo inscrito ela vai ser igual a 140 que a medida do ângulo central / 2 pode fazer a conta direto só tô representando tá então x vai é igual 70 que é o que 140 / nós então assistir vários 70 pronto gente conseguir encontrar nesse outro caso aqui veja aqui o arco agora Ele trouxe o arco e não ângulo central mas vai dar na mesma né você percebeu então o ar que a 55 Qual que é a medida do X então a medida do X que ele é um ângulo inscrito vai ser

a medida do a arco correspondente que a 55 / 2 então x vai ser igual vamos fazer cálculo mental 55 / 2 20 quanto 27,5 27,5 graus ai Pronto terminei nesse outro caso aqui o produção misturou agora em será que dá certo ao contrário agora ó aquilo 55 a referente ao ângulo inscrito porque ele a circunferência e aqui o X é do ângulo central porque o vértice dele ao ângulo aqui abertura está no centro então quer dizer que agora é o contrário a medida de X vai ser igual ao dobro do ângulo inscrito Então vai

ser igual a duas vezes 55 porque gente né ó na lógica né se o ângulo inscrito a metade do Central o Central é o dobro do inscrito tá bom Marca aí para você não esquecer Então nesse caso x vai ser igual duas vezes 55 110° Prontinho gente e nesse outro caso aqui olha como é que tá engraçado esse desenho bom eu sei que aqui ó é o centro então aqui eu tenho um ângulo central e esse ângulo aqui que mede 13° é um ângulo inscrito ó si um ângulo inscrito é 13 Olha bem aqui eu

não tenho o arco com Oi gente vai esse ângulo inscrito Então esse arco é o dobro é 20 100 graus e aqui esse arco não é referente a esse ângulo central e quando eu tenho o arco o ângulo central vai ser igual a medida do arco Então quer dizer que nesse caso x vai ser 26° nossas mas esses exercícios são muito simples aí eu já vi no minhas atividades que tem com x + 8 não sei o que Então veja que esses outros exercícios vamos ver nível 2 eu vou fazer em outra aula para você

você marcou bem essa aula aqui ó deixa eu fazer um resuminho aqui ó Então você aprendeu o que que o ângulo central vou colocar a ser de ângulo central Ele é igual a medida do arco Ok tudo bem aí você viu o também que a medida do ângulo inscrito ai ai mesmo que não pertençam a medida do ângulo inscrito O que é a medida do ângulo central / 2 tá bom E também você pode pensar que a medida do ângulo central vai ser duas vezes a medida do ângulo inscrito que é o dobro que é

o que eu fiz aqui as duas vezes a medida do inscrito marcou bem gente essas três casos que pode acontecer algo escrito a metade do Central e o Central do Brasil inscrito e aqui a medida do ângulo central é a mesma medida do arco correspondente E aí gente que que você achou dessa matéria dos ângulos na circunferência bem tranquilo né bem fácil de fazer então não deixe de deixar aquele like pra gente e se inscrever no canal compartilhar a aula com seus colegas e também ó visite o site da gis correios.com.br e lá você vai

encontrar listas de exercícios e a próxima aula também que eu vou fazer de ângulo inscrito e eu vejo você Como afinar aula tchau