COORDENADAS POLARES #01

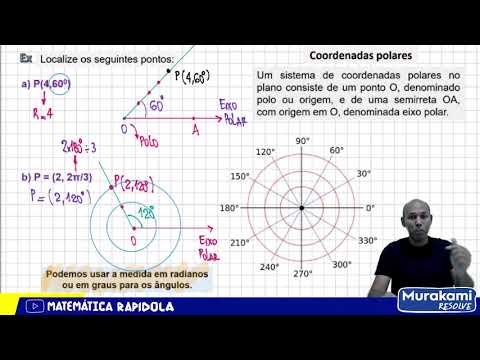
E aí [Música] e nós vamos conversar de um sistema de coordenadas que nós chamamos de Polar sistema de coordenadas polares como é isso Professor cheguei aqui eu tô bugado não tô entendendo essa história de coordenadas polares meu querido preste bem atenção eu vou começar direto na situação localize os pontos esse ponto aqui quatro e sessenta graus professora não entendo o que é isso venha cá vamos lá para gente compreender legalzinho primeiro no nosso sistema de coordenadas polares você vai ter alguns referenciais um eixo que nós chamamos de eixo polar Então vou colocar bem aqui com eixo como referencial esse carinha bem que o meu eixo polar então aqui eu tenho o meu eixo polar Escreva aí eu quero que você anote juntinho aí bem aqui eu tenho um eixo polar é que aqui na teoria eu até chamei de o ar porque o a que seria a origem essa origem aqui alguns professores chamam de Polo bem aqui você tem o seu Polo e aqui você tem um ponto a como referencial para você ter essa semirreta aqui lá que eu chamado e chocolate ela mas para que serve isso o que essa sua semirreta vai ser o nosso referencial porque quando aqui aparecer esse valor filhão 60 graus O que é isso é o angulo que ângulo que esta semi-reta está formando com uma outra então eu vou imaginar eu posso pegar o meu compasso desenhar que uma abertura de 60 graus e passar essa semirreta saindo aqui da sua origem do seu Polo bem aqui você vai passar uma semi-reta anote aí filhão vamos colocar de verde aqui essa semirreta também aqui eu tenho uma semi-reta e essa semirreta pelo Poder da Fé que eu tenho está formando um ângulo aqui com meu eixo polar um ângulo de quanto 60° é esse é o nosso esquema Essa é a sacada que você tem que ter a própria já entendi eu tenho este o colar aí aqui no Polo eu passo uma semi-reta uma abertura formando com esse eixo polar um ângulo de 60° sim legal e esse quatro Esse quarto é o seguinte a distância a distância de um ponto que você aqui é uma reta esse de verde aqui essa reta é formada por infinitos pontos mas você não vai pegar qualquer um você vai pegar um pontinho dessa sua semi reta de tal maneira que a distância é um número 4 esse quatro aqui é a nossa distância que alguns professores chamam de ro eu vou chamar Rua um pezinho é tipo um pesinho o Draqui é o meu R que vale quatro e aqui é o meu ângulo 60 graus aa e bem aqui você coloca o ponto filhão esse ponto bem aqui quatro e sessenta graus é aqui que está a representação em coordenada polar você entendeu Como funciona e esse ângulo professor ele pode ser grosso até coloquei as observação para você podemos usar a medida em radianos ou em graus é você que decide por exemplo nessa questão na B eu tenho ponto aqui dois e dois filhos / 3 a professor eu não sei o utilizar essa história de Pi eu tô bugado bem aqui ei uma dica rapidola para você no lugar do PPI você coloca 180 E aí você faz as contas que conta Professor filhão você multiplica por 2 e depois de vídeo por triste duas a 180 360 / 3 120 A então aqui é o meu ponto dos e o ângulo a que de 120 Girls sim dessa maneira vamos representar a própria como é que eu faço primeiro você pega o nosso referencial quem é o nosso referencial o eixo polar também aqui eu tenho um eixo polar pode fazer uma linha aí bacana aí no seu caderno e chocola vem aqui eu tenho meu Polo que a origem e aí eu pego eu compasso e preciso formar um ângulo de 120 graus 90 é assim 120 é um pouquinho maior Então 120° deixa eu colocar desse de Las aqui eu vou colocar um verde coloca bem aqui a minha cm reta está bem aqui uma semi-reta E aí você tem um ângulo esse ângulo formado aqui de 120° E essa semirreta você vai contar uma distância vai colocar na unidade de medida 11 por exemplo aí e aí você coloca um 1 cm daqui ó 12 Opa acabou o que é dois esse dois é a distância então aqui está o meu. P esse meu. P é o ponto 2 e 120 graus Não é dessa maneira que você representa o seu ponto em coordenada polar mural o que você fez esse desenho do lado porque eu gostaria que você percebesse que em verdade em verdade eu vos digo quando você faz isso aqui você tá fazendo circunferências concêntricas você percebeu isso eu posso tentar desenhar aqui algumas circunferências vou colocar bem aqui teria uma circunferência de raio 1 aqui uma outra circunferência de Raio 2 Então são circunferências concêntricas circunferências o mesmo centro A única diferença que você vai ter aqui ó é a distância essa distância chamei de raio não foi à toa porque o raio de cada circunferência Então esse ponto P é um ponto que ele pertence a uma circunferência de Raio 2 que é a minha distância e de propósito Eu chamo de raio para ficar bem entendido e esse 120° é o meu ângulo de rotação Então isso que a coordenada polar e é esse que você tem que saber agora Lógico eu tô aqui eu tô querendo que você aprenda Esse é meu sonho eu tenho um sonho com você que você aprenda esse tão não posso parar só aqui eu preciso te ensinar mais alguns detalhes duas perguntas no mínimo primeira pergunta seria esse um ângulo for negativo outra pergunta é possível eu tô aqui tentando resolver uma questão eu tô bugado que apareceu menos dois e aí você falou que esse menos dois é o raio e pode ser negativo como é que eu faço isso vocês querem inventar no sinal de menos copia que eu estou voltando e vamos resolver aqui essa situação nunca disse o seguinte pontos os seguintes pontos ele termine outras coordenadas polares que os representem preste atenção primeiro queria bater um papo com você legal pode aparecer na sua prova aí uma situação quando esse cara que é negativo Primeiro vamos transformar para Girls que tá mais fácil para você marcar esse ponto aqui é o meu ponto que você coloca assim o meu R meu r o que é que sempre assim você tem horror né ou então r o Ro é o pesinho lá invocadinho pesinho a cena é que alguns professores Coloca esse rolo aí bom então tenho bem aqui o meu vô e eu tenho meu ângulo só que esse ângulo aqui é negativo e apareceu o pi / 4 como é que eu tenho a forma para Girls no lugar do PPI você coloca 180 E aí dividir por 4 vai dar 45 E aí você tem a forma rápido a isso aí na manha tão bem aqui menos 45 Mas assim mesmo é estranho porque você deveria ter percebido na minha fala se eu não reforcei vou reforçar que esse ângulo quando você marca lá é no sentido anti-horário É nesse sentido aqui só que veio - 45 como é que vou montar - 45 aqui não - 45 É no sentido horário A então bugou agora Professor Calma que eu vou te ajudar bem aqui você coloca o nosso eixo polar aqui é na manhã na Mãe venha cal e coloca o nosso eixo polar bem que choro milhão Deixa eu fazer aqui e chocola para você entender escreva direito isso aí e chocola bem aqui o tenho meu Polo tem o nosso Polo aqui meu sozinho agora eu vou ter uma reta né uma semirreta ou uma reta se você quiser passar logo formando um ângulo de menos 45 é menos 45 eu saio nesse sentido aqui vou ter menos 45 graus bom então agora vou passar aqui a minha semirreta e pronto vai logo passar exagerado aqui para você perceber um detalhe passar aqui uma reta também aqui está a nossa reta eu posso dar uma puxada bem aqui jogar um pouco mais para cá para bater certinho que a gente quer está aqui a nossa semirreta e aqui você vai montar a reta né e aqui você vai montar o seguinte uma distância de quatro unidades você vem aqui marca não vou fazer muito longe só vai invadir o espaço da próxima na questão Um dois três quatro então parou bem aqui então se você quiser eu posso agora até recolher aqui Oi tá bem aqui tá bem aqui vai estar meu ponto Esse é meu ponto esse pontinho essa extremidade aqui é o meu ponto que ponto é esse a professor é o ponto 4 e menos 45 Esse é o meu.

4 e menos 45 graus C é só que ele pede para marcar né localiza a localizei está aqui o nosso. P só que ele pede um detalhe especial que eu represente de uma outra maneira que caísse no mesmo lugar seria esse o grosso Monster esse aqui é 14 - 45 não poderia ter uma outra acarica isso mesmo assim bastava você lembrar que você se deslocou 45 aqui no sentido horário E por que não no anti-horário o que se você observar a soma tem que dar presença senta Girls eu estou te dizendo pequeno gafanhoto que aqui você tem um ângulo Oi e a soma desse ângulo de vermelho com esse interno é bem aqui tem que dar presente 6045 mais alguém tem que dar 360 ou faça aí 360 - 45 que valor é esse aqui 315 eu estou te dizendo se eu representar esse ponto dessa maneira quatro e 315 é o mesmo. Está no mesmo lugar tá bom então tem essa maneira tem essa outra maneira e logo posso te dizer tem várias maneiras mas porque o que eu posso dar várias voltas eu poderia chegar aqui 315 a professor vamos dar mais uma volta aí tu pega a 315 e macho 360 a posso dar duas voltas sim quantas voltas você quiser então não há uma única representação vez que ele fala né e determine outras representa aqui quem quiser colocar mais aí fique à vontade fica como exercício a cada 360 graus você vai cair no mesmo lugar passa lembrar essa história lá da trigonometria né que é de lá que vem isso né Essa Ideia está lá vão ver se o exemplo porque aqui que a galera buga gente é aqui que mora o perigo como daqui aparece o sinal de mente Olha eu vou logo te contar porque às vezes ficar aí fica bugado que eu vou explicar uma coisa aqui ele acha difícil que eu vou falar na praça eu vou falar é o seguinte bem aqui você só faz um favor primeiro quando aparecer em radianos você pode facilitar sua vida e colocar o resultado em graus no lugar do PPI coloque 180 dividir por três essa equivalência é sempre a para transformar de graus para radianos né e radianos para graus está presença equivalência que pia equivale acento é 180 dividido por 3 Vai dar 60 e aí você Então coloque bem aqui 60 e aqui está o esquema se você quer apenas chegou aqui que é só terminar questão que ir embora eu vou te ajudar te ajudar porque ir embora então termina logo a questão esquema seguinte toda vez que aparecer negativo né a gente fala tem que ser nós definimos é uma convenção O que é esse menos dois estranhos e negativo que esse menos dois aí é meu raio ele é a minha a distância menos dois o que quer dizer menos dois quando vocês colocam quer dizer o seguinte se aparecer essa ideia do menos dois é a ideia de você fazer esse esquema aqui apareceu menos você pega o oposto se tá menos dois você pega mais dois esse é o nosso esquema E aí você pega mais um detalhe pega esse ângulo aqui até senta sempre 180 graus você aumenta então a e depois e o valor ac240 então aqui está a nossa inscreve aí é só desenhar Meu desenhar o mais fácil chego bem aqui posso desenhar para você ele pediu né para localizar não deixa eu e o localizar para você esse carinho eu tenho bem aqui vou colocar aqui um eixo colar a Cadê a minha ratinha bem aqui eu tenho meu eixo colar está aqui aqui colocar uma setinha uma setinha meu ó meu Polo aqui o eixo polar aparecendo aqui do meu lado eixo colar está bem aqui ó quase em cima meu eixo polar e eu tenho ângulo de 240 Girls 240 seria por aqui eu tenho 180 passa um pouquinho mais então seria por aqui esse 240 é você ter uma ideia deixa eu puxar essa receitinha não vai dar vai ficar aí mesmo ou eu tento desenhar mais uma vez para encaixar certinho ali no vazio E aí agora vem esse é meu ângulo lógico Gente eu estou desenhando aqui a mão livre aqui é o meu ângulo 240° positivo positivo no sentido anti-horário que a convencionar no sentido positivo nesse sentido aqui né é o horário negativo anti-horário A positivo e aqui você tem uma distância de duas unidades uma duas unidades Então esse é o meu.

É a representação do ponto menos dois e pi dividido por 3 ou então essa outra maneira para representar ele dois e 240 lembra aquela observação que eu posso dar mais uma volta vou pegar a 240 somar mais 360 tem uma outra representação dois e aqui o valor que você vai ter que você pegar 240 mas 360 e vai dar dois e seiscentos graus é o mesmo cara então cuidado quando for negativo é assim que se faz mas eu queria ainda eu acredito muito em vocês eu queria fazer você entender um pouquinho essa ideia que aqui ó essa história de virar positivo como é essa história história o seguinte quando vier essa simbologia ou Colocar assim vem aqui eu tenho meu ex o colar bem aqui está meu eixo colar Coloca ele sabe o nome né E este colar bem que eu tenho o meu Polo e aqui o meu socorro que eu tenho por exemplo um carinha que vale que eu vou chamar assim de menos R esse cara vou puxar aqui Oi e aí estar vindo com essa pérola de chamar até medir Não é esse aqui é o menos R E esse. - RT tá esse teto esse ângulo bem aqui hoje esquema quando aparecer essa simbologia menos reta é como se a gente rebatece amor eu não entendo como rebater se está aqui ó esse cara é minha extremidade pelo menos reta Eu vou rebater ele na mesma linha na mesma reta bem aqui só que eu vou rotacionar ele eu vou pegar o oposto dele então se aqui é o menos é eu vou pegar aqui o mais R é aonde e vai estar só para você entender esse giro bem aqui que a gente faz então essa representação do - TRT reta a gente tem essa visão essa ideia pega bem aqui e você rebate rebati deixa eu colocar mais para cá Oi e aí você tem esse cara bem aqui quando que vai ser a nossa simbologia ao nosso.