ÍNDICES DE MILLER - O que é, para que serve e como calcular!
107.5k views1444 WordsCopy TextShare

Hudson Zanin
Olá colegas,
Esta VÍDEO AULA busca introduzir os conceitos dos índices de Miller para descrição de p...
Video Transcript:
Olá pessoal hoje nós vamos falar sobre direções e planos cristalográficos utilizando uma ferramenta chamada índice de mirer esse tópico é de especial importância principalmente porque materiais possuem propriedades anisotrópicas em alguns casos ou seja suas propriedades dependem da direção e dos planos da medida por exemplo você pode determinar planos de clivagem de um cristal onde seria mais fácil de cortar de lapidar esse Cristal porque as as forças de ligações seriam mais fracas você poderia encontrar diferentes índices de refração no material B refringente por exemplo mas antes de entrar na questão das propriedades nós vamos falar como
definimos esses planos e índices cristalográficos vamos começar aqui com o caso das direções Vamos definir uma posição como a nossa origem onde colocaremos os nossos eixos de coordenadas x y e z Então a partir daí Vamos definir setas vetores que V dar direções em em e nesses nessa rede cristalográfica tá então vamos pensar primeiro caso aqui ó Desse exemplo onde nós temos esse vetor aqui como é que poderíamos dar uma orientação para que nós entendemos que esse vetor está representado sem visualizar a figura por exemplo veja que no eixo X el corta em zer no
eo Y ele corta no valor máximo da rede e no Z também então esse aqui seria a direção o vetor de direção 0 1 um veja que é representado entre colchetes quadrados tá e não há vírgula entre esses números que indicam as coordenadas do vetor sempre a base do nosso vetor vai estar na origem ou transladada Mas a partir da origem nós vamos desenhar essa ca e a coordenada vai ser em relação a essa ponta aqui então vamos ver um exemplo outro qualquer por exemplo vamos identificar essa direção 1 0 z0 vamos ver como desenhamos
esse vetor da origem caminhamos x até o valor máximo que é 1 e y até em zero então ele permanece Onde está e z também Zero então a intersecção é nessa posição aqui e o nosso eixo o nosso eh Nossa direção 1 está nessa posição aqui tá por exemplo vamos desenhar esse vetor e vamos identificar as coordenadas desse vetor da direção qual é essa direção Então veja que em X intercepta em um no valor máximo em Y não intercepta só em zero e em Z no valor máximo Então seria máximo em 1 em x máximo
é 0 em y e máximo em Z então teríamos 1 0 1 tá agora vamos ver o caso onde a gente tem esse vetor aqui ó com a direção negativa representado com essa Barrinha em cima do número 1 0 1 por exemplo então tem uma sugestão que eu dou aqui é que você transl o seu eixo de coordenadas na direção do número negativo mas adicionando uma unidade na direção positiva então aqui ó como o nosso eixo negativo o valor negativo é em x a gente quer a gente faz isso para representar o vetor dentro da
ca célula caso contrário Ele ficaria fora então qual é qual é a dica transl um no eixo X e coloque um novo novo eixo de coordenadas ali nada impede que você tenha um uma segunda Ah uma segunda origem então seria um Y linha por exemplo um X linha um z linha e essa aqui passa a ser sua nova origem certo então para representar aquele vetor aquela direção ali nós ah partirmos da origem como sempre e iríamos para valor -1 em x 0 em y e 1 em Z Então esse é o valor então essa aqui
é a ponta do nosso vetor e então ligari a base e a ponta tá E esse aqui é o nosso vetor -1 0 e 1 fica uma dica uma dúvida como colocar como expressar vetores que têm valores maiores do que é uma unidade um vetor como esse por exemplo a dica que eu dou é que você reduza esse vetor a um número unitário Então esse cara aqui ó era O negativo ficou em -1 Du ve 0 0 e 1 ou seja é o mesmo vetor que a gente tá representando aqui que a gente acabou de
representar porque esse dois aqui simplesmente dá noção de intensidade que não nos interessa nesse nesse nessa altura aqui para definir direções e tudo certo quero chamar atenção agora para um caso específico desse vetor aqui ó como representariam esse vetor se tomarmos nossa origem antiga poderíamos ter algum problema ficar difícil de visualizar mas um jeito de você ah visualizar mais fácil por exemplo esse vetor é simplesmente introduzir uma nova Origin nada impede você ter uma x duas linhas um Y duas linhas um z duas linhas você pode pôr quantas origens você desejar tá E aí esses
valores são relativos Mas eles descrevem perfeitamente a direção independente do referencial Veja essa direção aqui ele alcança o x duas linhas agora no valor máximo o y em zer e z em zer tá nunca vai cruzar o nem o x nem o y duas linhas e nem o z duas linhas logo essa direção é 1 0 0 Veja essa daqui esse vetor que a gente apresentou há pouco é o mesmo vetor por isso esses vetores fazem parte de uma família de direção 1 1 0 0 Então por analogia esses vetores aqui na parte superior que
apontam nessa direção também devem fazer parte dessa família tá perfeito vamos ver os planos Ah o detalhe é que no caso das famílias de quando você tá se referindo a famílias de eh direções você usa esses colchetes triangulares ou sinal de maior e menor tá no caso dos planos eu vou desenhar rapidinho aqui três redes cristalográficas Então como fizemos nos planos nós definimos uma origem e colocamos o nosso eixo de coordenada x y e z vamos começar aqui com com com meu plano Predileto o um um um que é o mais simples deles e os
planos nós eh definimos no índice de Miller entre parênteses e sem vírgula tá como no no no caso dos das direções então aqui basta a gente identificar onde eh essas orientações aqui cruzam no eixo x y e z e a gente vê que é no valor máximo da célula então basta unir os pontos e a gente vai ter o Plano 1 1 1 tá esse plano é gigantesco que vai ao infinito é muito grande só que dentro da célula ele tem essa aparência triangular vamos continuar aqui o nosso raciocínio e identificar um segundo plano então
definimos primeiro o nosso eixo de coordenadas nós queremos identificar esse plano aqui ó qual seria o índice de Miller para esse plano agora ele intercepta o X em 1 o y em meio e não intercepta o z por isso vamos colocar como nem no infinito então para isso a gente tem que tomar o recíproco tá ou seja quem tá no denominador vai pro denominador e quem tá no denominador vai denominador fica 1 sobre 1 não muda nada nesse caso aqui fica 2 sobre 1 e aqui fica 1 sobre o infinito Então esse plano pode ser
representado como 1 2 0 tá 1 2 0 entre parênteses né porque é o índice de planos agora vamos ver mais um caso aqui o primeiro passo é definir a origem x y e z ela pode ser em qualquer lugar onde você preferir tá agora vamos ver os planos e por exemplo 0 1 esse plano 1er ele intercepta o X em 1 no valor máximo mas não intercepta nem nem o y nem o z então ele vai ser essa Face aqui ó do cubo veja nunca toca o y nunca toca o z tá outra maneira
de dizer seria 1 sobre infinito e infinito e tomo o recíproco dos dois 1 sobre 1 fica na mesma 1 sobre infinito Então seria 1 0 0 certo e o plano 00 o plano 01 Nunca intercepta nem o x nem o y somente o z por isso ele é o topo desse cubo aqui e por analogia o 0 0 é esse é essa Face do cubo aqui todos devem estar entre parênteses porque são planos e eles formam uma família de planos que só são diferentes por conta da orientação então a gente pode definir aqui ó
1 só a a questão do referencial que diferencia os planos então é a família de plano 1 então isso a gente tem uma primeira visão de como nós descrevemos os as direções os planos e por enquanto é isso Tá certo muito obrigado
Related Videos

11:34
Defeitos em cristais: 0 a 3D
Hudson Zanin
17,436 views

22:22
SISTEMAS CRISTALOGRÁFICOS: 14 de Bravais
Hudson Zanin
40,380 views

35:07
Densidade Linear
Euliane Jesus
25,596 views
7:13
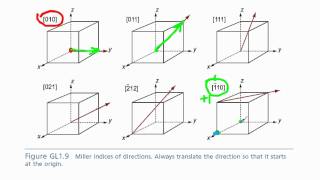
crystallographic directions
Linda Vanasupa
697,280 views
10:29
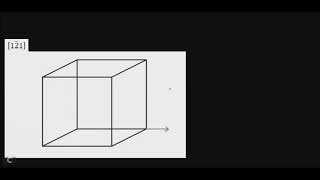
Planos e Direções Cristalográicas 1
Juliano Oliveira
13,380 views

8:20
Working with Crystallographic Planes and M...
Scott Ramsay
271,284 views

13:03
Direções Cristalográficas - Dificuldades p...
Prof. Danielton Gomes
19,055 views

14:47
VOCÊ CONSEGUE CALCULAR O TAMANHO DESSE LOTE??
Matemática com AMORim
1,976,020 views

19:42
METAIS, ISOLANTES e SEMICONDUTORES. Você c...
Hudson Zanin
24,900 views

20:07
Videoaula | Estrutura Cristalina e Imperfe...
Roberto Lima
40,448 views

21:41
VOLUME E CAPACIDADE! NUNCA MAIS ERRE ESSE ...
Matemática com AMORim
895,759 views

28:38
Ciência dos Materiais - Aula 01 - Por que ...
UNIVESP
216,716 views
27:14
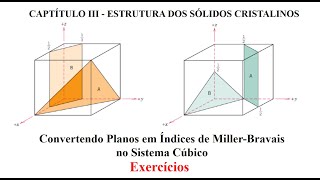
Convertendo Planos em Índices de Miller-Br...
Engenharia Raiz
21,181 views
![Planos Cristalográficos e os Índices de Miller. [Identificação e Notações]](https://img.youtube.com/vi/NnQWgNd5u9M/mqdefault.jpg)
8:07
Planos Cristalográficos e os Índices de Mi...
From Metal Till Now
1,070 views
13:47
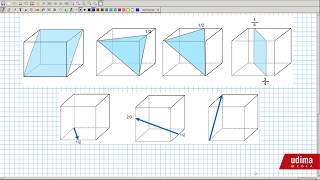
Obtención de índices de Miller de direccio...
Profesor Lucas Castro
91,381 views

12:23
Indices de Miller (Miller indices)
Ciencia y tecnología
138,294 views

34:31
Ramanujan: Making sense of 1+2+3+... = -1/...
Mathologer
3,398,844 views

11:09
Como calcular área de terrenos regulares, ...
Dicas do Fred
265,926 views
11:11
Aula 3 – Sistemas cristalográficos.
Engenharia vídeos
4,689 views
10:04
Lei de Bragg para cristalografia
Paulo H. Roesler
22,980 views