Cálculo I - Aula 17 (2/3) Concavidade e inflexão: exemplos

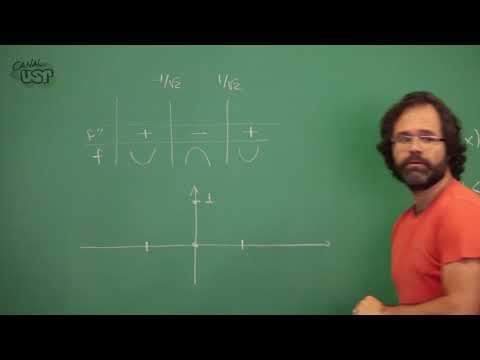
[Música] vamos fazer um exemplo com uma função bem importante está elevado - x ao quadrado vamos fazer tudo o que a gente consegue até agora que é o que estudar os intervalos de crescimento e de crescimento e todas as concavidades como é que determina os intervalos de crescimento e de crescimento dessa função a primeira derivados na então olhar pra f linha de x quem é fininha dx que a gente calcula derivada disso a regra da cadeia direto não é derivada do exponencial ela mesma mais pra frente vezes a derivada do que está dentro dos policiais

que quanto menos 2 x 1 na qual é o comportamento dessa função qual é o sinal dela a exponencial sempre positiva tá certo então que quem manda no crescimento é de crescimento é um fator menos 2 x 1 qual é o comportamento do menos 2 x troca de sinal 10 né então é fininha quando x é negativo tudo isso aqui dá positivo quando chega é positivo isso aqui fica negativo então você sabe que há é uma função estritamente crescente até 10 e estritamente decrescente depois do 0 o que a gente pode concluir disso esse ponto

aqui é um ponto de máximo local depois se você quiser tudo o que que é que acontece do ponto de vista global dá pra fazer também não é você consegue mostrar que esse ponto de máximo global da função que não teria garantia de existir porque a gente está olhando a função definida em toda reta real é bom o crescimento é esse com qualidade como é que são os com cavidades em vista desse problema que a gente acabou de olhar o que eu posso fazer para estudar com qualidade efe duas linhas quem efe duas linhas de

levar essa expressão aqui que agora é um produto legítimo na certo então como é que deriva isso ele fala do primeiro - 2 ea - x quadrado ele foi o primeiro golpe o segundo mais copiam o primeiro entre o segundo enquanto que dá vai ficar menos 2 x vezes a derivada dessa elevada de si é ameno x quadrado a derivada x quadrado - 2 x com esse - 2 x + 4 x quadrado tá bom como é que você pode escrever isso 4 x 2 - do boto 2 em evidência se você quiser bom e

de novo quem vai te contar com cavidades tudo ao sinal desse objeto como é que é o sinal desse objeto isso aqui é sempre positivo quem vai mandar no final esse termo que é uma função de segundo grau a gente sabe direitinho o que acontece então vamos montar como é que chama isso você só no varal zinho o varal do a gente tem agora duas raízes quais são os pontos onde efe duas linhas valorizar os pontos que a mão àquele por nome né e 2 x quadrado - 1 a 0 quando quando x for mais

ou menos 1 sobre raios de dois né então - um sobre raios de 21 sobre raios de dois vou ter o efe duas linhas e vou poder dizer o que acontece com a efe bom já em vista do que a gente falou agora mas se você sempre soube aquele polônia que está ali dentro do parente system com qualidade pra cima né sem conca verdade pra cima ele é positivo antes da menor raiz e depois da raiz maior negativo no meio então sinais aqui são positivo e negativo e positivo que isso quer dizer a segunda derivada

é positiva em todo esse intervalo então a função tem qualidade pra cima nesse intervalo série negativa aqui com qualidade para baixo depois com qualidade possível a gente sabe exatamente como que a função cresce decresce e qual é a concavidade em cada intervalo de crescimento de crescimento tá bom pergunta quais são os pontos de inflexão nos pontos onde muda concavidade exatamente esses dois está nesse caso calhou de ser exatamente os pontos onde efe duas linhas vale zero porque isso porque efe duas linhas é uma função contínuo gente eu vou escrever isso daqui a pouquinho da sua

função uma função de classe c2 todo ponto de inflexão satisfaz efe duas linhas igual a zero é tipo um teorema de fermat para a segunda derivada que o teorema de fermat dizia você tem uma função derivava eu tá esse um cara ponto de máximo então a primeira derivado de zero qual é o análogo aqui se você tem uma função duas vezes derivava eu a segunda derivada contínua se um cara ponto de inflexão então segundo privada tem que ser zero bom dá pra mostrar isso fácil mas vamos concluir só a gente tem então os intervalos de

crescimento e de crescimento com cavidades isso te permite com um certo na verdade com grande grau de precisão tentar estudar como é que um gráfico dos a função agora quais são os pontos interessantes que apareceram pra gente o zero que é um ponto onde você tem uma troca de crescimento de crescimento e mais ou menos 1 sobre raios de dois vão marcar esses pontos com 11 pontos interessantes eu sei que esse ponto a função vai ter algum valor vamos preocupar em calcular isso agora está no zero a função vale um claro aqui ela vai ter

algum valor aqui outro eu sei que esses pontos um ponto de inflexão o que acontece com a função quando x tende para - infinito isso aqui tem de pagar quanto a primeira observação esse valor e troca de sinal é sempre positivo sempre negativo que dá pra dizer exponencial a imagem sempre positiva tá então quando for desenho gráfico dessa função ele vai estar todo dinheiro pra cima do eixo x ótimo que acontece quando x é muito negativo quando se estende para - infinito quando se estende para - infinito x ao quadrado tende para mais ínfimo itu

e portanto eu tô calculando exponencial de um número bem negativo como é que é exponencial de um número bem negativo tende a zero sarto gráfico do elevado x é assim se eu pego um x bem negativa substituiu aqui o resultado vai ser um número bem negativo voltar com uma quantidade cada vez mais próxima de zero então esse gráfico ele começa bem próximo dos comércios não porque não tem começo não revelado - infinito ele está cada vez mais próximo de zero o que acontece até 10 ele vai ser sempre crescente e como é que ele cresce

ele vai ser crescente de boca pra cima até esse ponto então ele é crescente um boca pra cima a partir desse ponto ele inverte a concavidade mas continua crescente até 10 tá bom do zero pra frente o que é que ele começa a fazer e aí começa a descer decrescente de crescente mas ainda de boca para baixo até esse ponto aqui ea partir desse ponto que vai acontecer ele vai continuar crescendo só que agora de boca pra cima e que acontece quando x vai para o infinito de novo voltar com esse potencial de um número

bem negativo vai para zero não tá muito perfeito porque o que se sabe de si gráfico essa função uma função para se trocar x por - x o valor da função variante então como é uma função para o gráfico é totalmente simétrica em relação ao eixo y então tinha que se metros eu fosse um bom desenhista qual é difícil não lembra da definição de função para a gente disse que é uma função nova função para si fdx é igual à efe - x quem quer dizer que dois pontos opostos tem o mesmo valor então o

gráfico é simétrico em relação ao eixo y que é uma função ímpar você vai ter menos fora que não não quer dizer que ela se metem em relação ao eixo x o que a assimetria que acontece se eu trocar se eu pegar um x que tem um valor menos x vai ter valor proposto então se o ponto x y está no gráfico quem vai estar no gráfico também menos x - y ele vai querer dizer que o gráfico em variante por uma rotação em torno da origem de 180 graus o que está no primeiro quadrante

pá para no terceiro e vice-versa o que está no segundo exemplos de função para o conselho de x x ao quadrado é um exemplo de uma função pac por exemplo já motiva uma coisa bem interessante que vai ficar clara depois você tem uma função x quadrado é simétrica ac x ao cubo é uma função importante porque se você troca x 1º x a conta é o que acontece esse raminho do x ao clube com esse componente está aqui você pega esse cara gira 180graus então tá aí a situação que a gente tem um exemplo concreto

e ver como isso aqui vai te ajudar a fazer o esboço de gráficos tá esse é um gráfico simples por enquanto que a gente fez e se você tentar usar alguma ferramenta computacional para fazer esse gráfico vai ter uma coisa bem parecida com a que diga a inclinação aqui é isso que você quer saber com a inclinação da reta tangente nesse ponto o que você pode pensar isso né que a reta tangente nesses pontos ser um ponto de inflexão quer dizer que trocou de concavidade então um ponto antes do ponto o gráfico está acima ou

abaixo e depois desse ponto o inverso da qual é a inclinação da reta tangente nesses pontos você vai ter que calcular a primeira derivada nesse ponto enquanto que vale quando x for - um sobre raios de 2 dar quanto você colocar aqui vai dar raio de dois né - vai ficar mais de 2 positiva e levado à vezes elevado - meio então é um é 45 graus para ser 45 graus esse número teria que ser um bom pergunta existe algum ponto onde só aqui vale um tem que tentar resolver essa equação como é que se

resolve a situação igual isso aqui é um só vai ter o qq elevado x ao quadrado tem que ser igual 2x existe algum ponto onde os gráficos dessas funções se interceptam como é que eu posso querer saber se existe ou não teria valor intermediário quero saber se uma função vale 1 como ela é contínua que eu faço acho um ponto onde é menor que 1 em um ponto onde ela maior que o valor intermediário alguém ali no meio vai fazer um tá bom esse povo tem que ser real 11 qualquer coisa se ele tem que

ser real ou qualquer coisa o que se chama de qualquer coisa complexo a gente não está tratando de números complexos aqui então quando eu estou procurando uma solução tem que ser uma solução real o teorema do valor intermediário lida com funções que chegam saem dr chego em que o cara tá te dizendo se um ponto ela valeu 0 no outro ponto ela falou 2 em algum ponto intermediário vai fazer um número real 1 agora se essa equação existe admite soluções complexas isso aqui é igual a 1 você tem que primeiro pensar o que é exponencial

complexo eu acho que vocês nunca viram isso se a solução a solução teria que ser real se você conseguir aplicar o teorema do valor intermediário ela garante que é real agora o que seria uma solução complexa para essa equação se você não sabe o que é um exponencial complexa que é elevado o número complexo a gente nunca tratou disso aqui e nem vai tá o que se sabe é soluções complexas para polinômios você vê um pouquinho disso na escola as equações que envolvam funções que não são por nomear mais podem ser tratadas com o complexo

também está mas não está no escopo desse curso tem o que é oceano de um número complexo no conjunto dos números complexos a equação sendo dizer igual a dois tem solução o número complexo sendo dizer não precisa estar entre - unb mas isso aqui não é um cálculo para funções de uma variável real é o que a gente está fazendo chega então basicamente segunda determina concavidade a segunda derivada determina concavidade do gráfico em cada ponto achar o ponto de inflexão é isso fica mais a cargo da primeira mão o ponto de inflexão o que é

um ponto de inflexão é onde muda concavidade o que eu uso para determinar concavidade segunda derivado então achar pontos de inflexão tá muito ligado com estudo da segunda derivada achar pontos dê máximo e mínimo tá ligado com a primeira derivada exemplo deu pra ver pela isso não a primeira derivada de conta como a função cresce como ela decresce a partir disso eu consigo concluir que esse ponto aqui é um ponto de máximo local eu não consigo dizer se ela cresce de boca pra cima de boca pra baixo tá você consegue imaginar uma situação dessas onde

aqui ela tem a boca para baixo uma parábola - x quadrado esse ponto a ponto de máximo eu tenho com qualidade para baixo tá então a só a primeira de elevada não te contar nada a respeito da concavidade da função lote conta a respeito do coeficiente agora em cada ponto então eu estou nesse ponto a primeira derivada não diz quem é o coeficiente angular da reta tangente essa função passa por esse ponto com essa reta tangente tem boca para baixo tem outra função que passa por aqui com o boca pra cima o que vai diferir

essa função dessa sabendo que ela passa por esse ponto e tem a primeira derivada que determina esse coeficiente angular o que vai distinguir a concavidade a segunda derivada da então isso é uma coisa que a gente vai vai ser interessante daqui a pouco quer dizer se eu te dou um ponto no plano em uma reta tangente tem várias funções que passam a te dou um ponto em uma reta quanto às funções existem que passam por esse ponto infinitas tá o que eu posso dizer de todas as funções que passam por esse ponto e tem essa

reta gente essa reta como tangente ao gráfico naquele ponto todas elas vão ter o mesmo valor no ponto x 0 ea mesma primeira derivada o que distingue duas funções que passam por aqui tem esse cara correto tangente a segunda derivada vai ajudar a distinguir a então por exemplo se passa por aqui com essa reta tangente tem segunda derivada negativa vai ter que ser uma coisa desse tipo você tem segunda derivada positiva vai ser uma coisa desse tipo agora só olhando as que têm segunda derivada positiva eu consigo tem duas funções que passam por esse ponto

com essa reta tangente e com qualidade para cima tem tem essa já tem uma outra que passa assim e aí isso vai medir o que o que vai fazer a diferença o quanto mais côncava ou menos com cabeça função é o que vai te dizer isso como varia a segunda derivada você tem que olhar pra terceira derivado da então duas funções que passam por esse ponto com essa reta tangente e com a mesma concavidade elas com certeza tem a mesma primeira derivada da mesma segunda derivada e o mesmo valor no ponto que vai distinguir a

terceira deriva prefeito desgosta gráficos a gente só vai fazer a análise da primeira e da segunda derivada porque eu já me dou por satisfeito em saber como ela cresce e cresce com uma concavidade como varia concavidade você poderia precisar estudar mas você consegue fazer um bom grau fico já com essas ferramentas já então observação importante essa aqui é tipo de um firmar pra comprar a ponto de inflexão tá se você tem q f é de classe c2 que quer dizer que é de classe c2 que ela é contínua deriva' viveu duas vezes derivava eu ea

segunda de elevada é uma função contínuo tá bom chefe de classe c 2 x 0 é ponto de inflexão df então com certeza efe duas linhas de x 0 e gozar tá uma sutileza ea mesma sutileza que o teorema de fermat vamos tentar se convencido porque isso é verdade tá supõe que efe duas linhas não é zero por exemplo é positiva então tem um ponto onde a segunda derivada é positiva por hipótese segundo elevado uma função contínua que isso quer dizer se ela é positiva nesse ponto é contínua vai ter um pequeno intervalo onde ela

continua positiva então cef duas linhas de x era positiva em função de classe c2 ela vai ser positivo no intervalo em volta do continente 0 que lhe garante se eu tenho um intervalo onde a segunda derivada positiva em todos os pontos desse intervalo a função tem concavidade para cima portanto esse ponto não pode ser um ponto de inflexão certo cf duas linhas por positiva onde existe um intervalo e onde efe duas linhas de x é maior do que zero escreve assim para x pertencente no intervalo aberto pelo teorema que a gente acaba de demonstrar a

segunda de elevada e positiva no intervalo em todos os pontos há concavidade pra cima e sair com qualidade pra cima em todos os pontos desse intervalo antes e depois do x 0 com qualidade é a mesma para cima portanto fizeram não pode ser um ponto de inflexão certo de maneira análoga ciac for negativo se não ponta negativa ela continua negativo em volta desse ponto e portanto ela teria que ter com qualidade para baixo em todos os pontos desse intervalo e portanto não troca de então se ela for de classe 2 e 1 ponto x é

um ponto de inflexão forçosamente segundo derivado de zero qual é o erro comum é o mesmo erro do teorema de fermat que teorema de fermat dizia que esse é ponto de máximo a um mínimo a primeira derivado de zero o que era falso que a primeira derivado de zero ponto de março mundo tá então aqui o que está dizendo que se for ponto de inflexão a segunda dele vai de 0 a segunda derivada for zero é verdade que fui aquele ponto um ponto de inflexão não temos um exemplo vagos né então cuidado de novo né

outra vez de escrever atenção em letras garrafais cuidado pega fdx igual x a quarta tá enquanto que vale é filhinho de x 4 x 3 enquanto que vale efe duas linhas de x 12 x ao quadrado enquanto que vale então efe duas linhas de 0 a 0 pergunta esse ponto zero é um ponto de inflexão do gráfico de she's a quarta não é porque antes do zero isso aqui é positivo boca pra cima depois do zero é positivo boca pra cima também tá então x a quarta o gráfico não é uma parábola né mas é

uma coisa assim bom nesse ponto a segunda derivada igual a zero esse ponto não é um ponto de inflexão do mesmo jeito que a gente usou x ao cubo para concluir que a derivada no ponto era zero e ele não era nem máximo nenhum então muito cuidado com isso aí então se eu estou procurando quem são os pontos de inflexão de uma função de classe c2 eu pego e olha o preço aqui quando resolveu essa equação eu vou achar os candidatos a ponto de inflexão a não quer dizer que eles sejam então tem um ponto

no segundo derivado de zero pode ser que ele seja um ponto de inflexão que eu preciso fazer olhar para os valores antes e depois para vencer concavidade mudou não diga joga muito bem a vamos fazer então uma técnica alternativa para calcular limite que é famosos super útil ea partir de daqui a pouco vocês vão poder usar tá que é o que a gente chama de regras do hospital