FRACTURE TOUGHNESS and Crack Modes in Under 10 Minutes!

part of maintenance procedures and parts that are already in service including inspecting for cracks and notches that have been developed during service an important part of manufacturing or production engineering consists on inspecting newly produced parts or even raw material for cracks flaws inclusions or defects before service begins analyzing these imperfections as an elastic stress concentration is almost useless as the smaller the imperfection the smaller the radius we use to find stress concentration factors which yield stress concentration factors that approach infinity relatively brittle materials are such materials that can fracture without yielding now brittle fracture is

not instantaneous crack propagation needs time for the energy to feed the crack but there is such a thing as an unstable crack size which would cause a material to fracture also not only brittle materials fracture most materials have a ductile to brittle transition temperature that bring even low carbon steel and strong aluminum alloys to a relatively brittle state when temperature drops today we will look at crack modes stress intensity factor stress intensity modification factor and fracture toughness we will focus on crack propagation one of the earliest fracture mechanics ideas studied stress field calculations for an

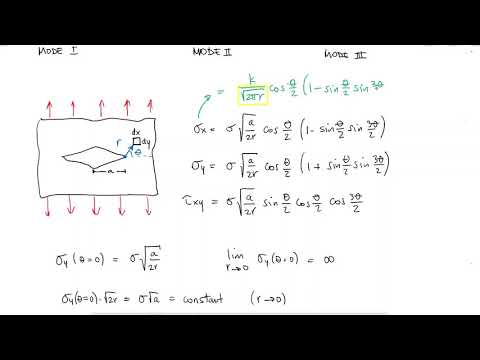
elliptical flaw in this case the maximum sigma y was given by the product of the stress concentration factor and the external stress but this model was slightly flawed as again for a sharp crack b would approach zero making sigma max approach infinity today we use three different crack modes a tensile stress that results in the opening crack propagation mode the sliding mode due to an in-plane shear and the tearing mode which results from out of plane shear and of course you can have combinations of more than one mode however since mode 1 is the most

common one we will focus on that one today using more complex stress field calculations for an infinitesimal element around the crack tip that i will not show today but you can check some references in the video description we have expressions for sigma x sigma y and tau xy if we look at the expression for sigma y when theta is 0 which is the plane where the crack exists we obtain an expression that depends on the external stress the crack length a and the distance to the crack r however just as with the elliptical crack example

we see that sigma y would approach infinity as r goes to zero however if we rearrange this expression we see that sigma y times square root of two r is constant and equal to the external stress times the square root of the crack length even for when r approaches zero because of this we call this constant the stress intensity factor and the reason we add a pi inside the square root is so that when i write my stress equations in terms of the stress intensity factor i find a square root of the circumference in the

denominator and since this stress intensity factor is only true for mode 1 of crack modes and i don't want to confuse it with other stress concentration factors such as kt or kts we label this one as k1 in roman numerals the units of this stress intensity factor are therefore mega pascals times square root of meters or ksi square root of inches so we know that the stress intensity factor is a function of the external stress and the crack length a but it makes sense that the values for these expressions will change if the geometry shape

or even location of the crack changes therefore the stress intensity factor is also a function of geometry shape and location and for this we use a stress intensity modification factor for which either beta or capital y is used a few examples for this stress intensity modification factor include a crack inside a plate in longitudinal tension a crack at the edge of a plate loaded in longitudinal tension rectangular cross-section beams that have an edge crack or cracks inside a circular hole inside a plate and tension once you have completed all the calculations to find your stress

intensity factor k1 you would compare its value to the critical stress intensity factor k1c which is a material property that depends on the material the crack mode the processing of the material temperature loading rate etc this critical stress intensity factor is also known as fracture toughness and since it's defined as a material property theoretically you could find its value for an engineering material some examples would be aluminum between 26 and 33 megapascal square root of m titanium between 55 and 115 and steels between 14 and 99 but these ranges are just examples the actual values

for fractured toughness are more often than not tested in a lab where you as a designer can find experimentally what the fractured toughness value is for the specific operation conditions like i mentioned before the ductal to brittle transition temperatures are very important to determine if your material is going to behave as a relatively brittle material and even then tables of transition temperature for different materials are not commonly published mainly because the values vary a lot a key indicator however is the ratio between the yield strength and the ultimate strength because a higher ratio means that

the ability to absorb energy in the plastic region is low and therefore there's a higher chance of brittle fracture the fractured toughness to the stress intensity factor ratio can be used as a factor of safety let's take a look at an example where we put everything we've learned to use we have a titanium plate in longitudinal tension that has a crack right in the middle we want to know what the current factor of safety is and the maximum tensile force before fracture would occur i know that to get the factor of safety i need to

calculate the stress intensity factor and to do that i need to find the tensile stress and the stress intensity modification factor beta the tensile stress would be equal to the load over the area and to find the stress modification factor i would use the charts or plots for this specific case an off-center crack in a plate in longitudinal tension for the modification factor i know that 2b is equal to 300 millimeters that since the crack is centered the distance d would be half of that making d over b 1 and that the crack that is

90 millimeters would make a equal to 45 millimeters notice that the x-axis is the a over d ratio which in this case would be 0.3 using the top curve for d over b equal to 1 and an x value of 0.3 i would find that my stress intensity modification factor is equal to 1.05 with these values i can calculate the stress intensity factor and by using the fracture toughness over that value i can find the factor of safety since the stress intensity factor is directly proportional to the stress and the stress is directly proportional to

the force the maximum force would be equal to the factor of safety times my current force if you want to check out other examples where we make use of the concepts that we've learned today make sure to check the links in the video description in the next video we will take a look at crack propagation crack growth equations which allow us to calculate the rate of crack growth per cycle and we will introduce the concept of fatigue thanks for watching