Entendendo tudo sobre Campos Vetoriais no R² e no R³ | Cálculo Vetorial
11.84k views5062 WordsCopy TextShare

Matemateca - Ester Velasquez
O que são Campos Vetoriais e como analisar graficamente?
Faça parte da plataforma Matemateca Academ...
Video Transcript:
O que são os campos vetoriais e como a gente representa eles graficamente vamos lá entender Oi gente meu nome é Ester Velasques e sejam bem-vindos a mais um vídeo do canal matemática nessa aula a gente vai começar a falar sobre Campos vetoriais entendendo o que é isso exatamente como a gente representa algebricamente e graficamente também tá bom então antes de começar Já curte aí embaixo se inscreve no canal e vamos lá gente então para começar a falar sobre Campos vetoriais vamos imaginar uma situação em que você tá estagiando em uma empresa que trabalha com meteorologia
e ele te deu a seguinte função você vai ter que pegar o mapa da costa do litoral ali do Nordeste e você tem que desenhar como tá funcionando o vento naquela região Então como tá a velocidade do vento ali então Sabe aquele mapa que tem uma setinhas mostrando como tá o vento em determinada região você vai ter que fazer isso aqui você vai ter que mostrar para o pessoal como tá o vento nessa parte aqui que tá ventando muito se a velocidade do vento tá alta você tá baixa em quais regiões estão ventando mais né
Então você vai ter que implementar esse mapa e para fazer isso você resolveu fazer o seguinte Você desenhou dois eixos um eixo horizontal que é o x e o eixo vertical que é o y e aí você vai desenhar para alguns pontos específicos Como tá a velocidade do vento Então você estabeleceu aqui como x = 0 aqui como Y = 0 e você vai começar a desenhar setinhas que representam o vento tá aí você vai começar pelo ponto onde x Vale 0 e y vale zero e você repara o seguinte não tem vento nessa região
nem para direita nem para esquerda e nem para cima ou para baixo tanto na horizontal quanto na vertical não tem vento tá valendo zero então aqui você vai deixar desse jeitinho mesmo né não vai desenhar seta nenhuma agora quando você vai para x = 1 permanecendo no Y = 0 você repara que você também não tem vento na horizontal Mas você vê que você tem uma componente de Vento pequenininha com valor escalar igual a 1 na vertical apontando para cima então na vertical Você tem uma componente 1 querendo dizer que a velocidade do vento ele
não tá tão alta no escalar além do só um né tá apontando para um aqui no Y Só que tem um vento né Tem algum vento acontecendo ali e aí a mesma coisa acontece quando você vai para x = 2 você repara que você não tem vento na direção horizontal ou seja não tá ventando para lá e nem para lá nessa altura mas você tem uma componente 2 na direção vertical Ou seja a velocidade do vento aqui deu uma aumentada não tá apenas um mas agora tá no dois o valor escalar dela o tamanho dessa
setinha tá indo até o 2 ou seja para essas duas setinhas aqui o vento tá na mesma direção mas para quem tá aqui nesse ponto vai sentir a velocidade do vento maior do que quem tá aqui nesse ponto aqui no meio do mar aí você resolve andar para a esquerda ao invés disso então você vem para um de x é igual menos um e o y permanece valendo zero ou seja você foi para o ponto menos um zero do seu mapa você Pare que aqui também não tem vento na direção horizontal mas você tem um
vento na direção vertical que tá indo no sentido contrário ao que estava antes então antes estava indo para cima né em direção a Sergipe agora tá indo lá em direção a Salvador lá para baixo e também com velocidade baixinha velocidade valendo um que é o tamanho dessa setinha aqui então ele tá apontando para baixo por isso tem sinal negativo e o tamanho dele é um tá aí você cansou de desenhar setinhas para o Y igual a zero você decidiu dar uma subida aqui e vir para o x = 0 porém Y = 1 então quando
X é zero e y é um você repara que você não tem vento na direção vertical mas você tem um vento na direção horizontal valendo um Ou seja você tem algo assim o vento indo só na direção horizontal Quando você vai para Y = permanecendo com x = 0 você não tem vento na direção vertical mas você tem um vento com uma velocidade um pouco maior na direção horizontal Agora o seu vento a setinha aqui tá com módulo igual a 2 que o vento tá com uma velocidade maior aqui nessa região agora vamos mudar a
cor para desenhar no ponto em que x = 1 e y é igual a 1 Então nesse ponto Amarelo aqui nesse ponto onde os dois valem um você repara que você tem uma componente de velocidade do vento valendo um na direção horizontal e valendo um na direção vertical Ou seja você tem algo assim para esse ponto aqui quem tá nesse ponto vai sentir o vento vindo tanto para cima quanto para o lado né vai formar esse vetorzinho aqui E aí quando você vai desenhando você chega nesse padrão aqui ó aqui tá onde a gente desenhou
um zero aqui o dois zero aqui é o zero um né os vetores que a gente desenhou para cada um dos pontos e o que você conseguiu reparar seguindo esse padrão aqui da setinhas é que a velocidade do vento aqui na Costa do nordeste está funcionando da seguinte forma em cada ponto x y que você tem aqui no gráfico que Você desenhou a velocidade do vento vamos chamar de v aqui a velocidade do vento nesse ponto x y vai ser um vetor que sempre vai apontar na horizontal para o valor de y e na vertical
tá apontando para o valor de X Então olha só aqui quando X era 1 e y era zero era zero não horizontal e um na vertical agora aqui quando X Era Zero e y era 1 era a segunda coordenada apontando no eixo horizontal e a primeira coordenada apontando no eixo vertical então você conseguiu reparar que você sempre tem esse padrão aqui ó para cada ponto x y o vetor que representa a velocidade do vento vai ser o valor de y o valor de X sempre nesse formato tanto é que aqui no zero ó não tem
vetor porque as duas componentes valem zero tanto x quanto Y então por exemplo essa seta grandona aqui ela tá no ponto onde x = -5 e y é igual a 5 Então esse vetor aqui se a gente for ver para onde ele tá apontando ele vai estar apontando para cinco na direção horizontal e para menos cinco na direção vertical então é como se fosse esse vetor aqui ó que aponta para cinco no eixo horizontal para menos cinco no eixo vertical só que a diferença é que a gente pegou esse vetor e deslocou ele até o
ponto menos cinco cinco a gente trouxe ele aqui para cima mas ele continua apontando para mesmo direção mesmo sentido e com o mesmo tamanho então gente basicamente o que você encontrou nessa tarefa do seu estágio é que o vento a velocidade do vento em determinado Ponto X e Y da Costa do teste tá funcionando dessa forma tá indo com velocidade Y na direção I que a direção horizontal e tá indo com Velocidade X na direção J que é a direção vertical então só lembrando quando tem ir a gente está falando do eixo X quando tem
j a gente está falando do eixo Y então se você quiser saber para onde está apontando o vento no ponto 32 desse gráfico aqui da Costa do Nordeste a velocidade do vento Vamos colocar ela assim vai ser a coordenada Y apontando na direção e mas a coordenada x que é 3 apontando na direção Y gente então repara que cada um desses pontos aqui da Costa do Nordeste vai ter um vetorzinho associado a eles é claro que a gente não desenhou para todos os pontos não tem como a gente desenhar cada um dos infinitos vetores nos
infinitos pontos mas olhando o gráfico por cima dá para a gente ter uma ideia de como o vento tá se comportando nessa região certo para cada ponto que a gente tem a gente tem um vetorzinho do vento associado a ele então para o ponto um zero tem um pro ponto dois zero tem outro para o ponto 53 vai ter outro vetorzinho cada ponto tá associado a um vetor que representa a velocidade do vento nesse caso então gente essa tarefa que você cumpriu ali nada mais é do que um campo vetorial que você fez para representar
a velocidade do vento você fez um campo de velocidade do vento ali e o que é um campo vetorial então um campo vetorial quando a gente tá no R2 então quando a gente tem um plano vai ser uma função que associa cada ponto então cada um dos pontinhos que a gente tem aqui ele associa a um vetor então cada um desses pontos vai ter um vetor associado a ele e o campo vetorial vai fazer essa Associação de acordo com uma determinada lei ele vai terminar ó para cada ponto x y o vetor vai ser p
na direção x e q na direção Y Então esse p e q são funções escalares não tem vetor envolvido nelas individualmente Pode ser que elas sejam por exemplo P de x y = 2x + Y e q de X Y Às vezes pode ser uma constante também então o que esse caso estaria falando para gente é que para cada ponto x e y que a gente tem a gente vai ter um vetor que é ponta para 2x + Y na direção do eixo X e aponta para três na direção do eixo Y isso é a
mesma coisa que escrever o vetor 2x + Y 3 esse aqui é o nosso vetor no Ponto X Y ou seja se você pegar o ponto um do seu plano o vetor F que esse campo vetorial vai gerar para ele vai ter coordenada 2x + Y na direção horizontal ou seja duas vezes x + y que no caso também vale um na direção do eixo X e vai apontar para o 3 de acordo com essa lei na direção do eixo Y então o vetor gerado no ponto 1 por esse campo vetorial aqui porque é essa
lei que a gente gerou aqui vai ser três na direção do eixo X e 3 na direção do eixo Y ou seja para esse caso o vetor que sai do ponto 1 vai ser o vetor 33 então o campo vetorial Como o próprio nome diz vai justamente gerar um campo de vetores aqui como eu falei anteriormente Claro que tem infinitos pontos infinitos vetores mas que a gente representa só por alguns para entender como é o comportamento daquele Campo naquela região específica então aqui a gente tem exemplo de Campo vetorial que tem essa lei ó ele
vai sempre apontar para o menos y na direção do eixo X e para o x na direção do eixo Y ou seja para cada ponto x y o vetor associado a ele vai ser um vetor que aponta para menos y no eixo horizontal e que aponta para X no eixo vertical então por exemplo se a gente pegar o ponto um zero aqui quando x é 1 e y é zero ele vai ter um vetor associado a ele que esse vetor vai apontar para Zero no eixo horizontal já que o y Aqui é zero e vai
apontar para um no eixo vertical então o vetor aqui é algo nesse formato e repara que quando o y é positivo então aqui acima do eixo X que é quando o Y tem valor expositivos as setinhas estão todas apontando para a esquerda porque no eixo horizontal a gente tá apontando para menos y esse o y que é ao vivo a gente está apontando para algo negativo entendeu E quando o y é negativo as setinhas estão todas apontando mais para o lado direito inclinadas para o lado direito porque se o y é negativo a gente vai
estar apontando para um número positivo no eixo horizontal Então se a gente tiver 2 - 3 quem é o vetor associado a esse ponto aqui de acordo com esse campo vetorial então f de dois menos três vai ser menos y na direção e então 3 na direção e e x na direção J então é o vetor 32 uma outra coisa que a gente consegue reparar aqui ó do lado direito X é positivo do lado esquerdo ele é negativo né do lado direito as setinhas estão sempre inclinadas para cima elas estão mais para cima do que
para baixo porque quando X é positivo a gente vai estar apontando para positivo no eixo vertical ao eixo vertical tá pegando o valor de X para ele tá pegando o valor de X para representar o vetor Então se o X é positivo a gente vai estar positivo no eixo vertical agora na esquerda que o x começa a ser negativo as setinhas vão apontando mais para baixo porque se agora o X é negativo a gente tá apontando para valores negativos em relação ao eixo vertical isso para essa lei aqui para essa função de Campo vetorial tá
bom E outra coisa que a gente pode reparar é que quanto maior o valor de x é maior o valor de y em módulo maiores são as setinhas Ó quanto mais distante a gente tá da origem as setinhas vão aumentando de tamanho é a mesma coisa que acontecia aqui quando a gente estava mais longe da origem as setinhas eram maiores porque os valores de x e y eram maiores em módulo né tipo tamanhos maiores em valores absolutos então isso quer dizer que nessas regiões a velocidade do vento era maior do que aqui próximo de Feira
de Santana de Salvador um outro exemplo de Campo vetorial no R2 esse campo vetorial tá falando para gente que para cada ponto x y a gente vai ter um vetor apontando para Y na direção horizontal e apontando para o seno de x na direção vertical ou seja o f de x e y para esse caso é um vetor onde a primeira coordenada é o valor de y e a segunda coordenada é o valor do seno de x Então primeiramente repara que quando o y é negativo no eixo horizontal a gente tá apontando para a esquerda
porque a primeira coordenada do vetor depende do Y esse Y é negativo a primeira coordenada vai apontar para algo negativo e quando Y é positivo todas as setinhas apontam para a direita Porque se o y é positivo as setinhas vão apontar para algo positivo no eixo fundamental agora em relação a segunda coordenada é o que está apontando para o eixo vertical isso vai depender do seno de x e a gente sabe que o seno de x não varia muito né ele só vai de -1 até 1 ele vai variando sempre Entre esses valores é por
isso que as setinhas estão com comportamento uniforme né ela sobe um pouco em relação ao eixo vertical descem um pouco mas nunca vão subir absurdos e nem descer muito aqui vai sempre mantendo um certo comportamento tanto é que em uma mesma altura Y que essa altura aqui a gente vê que as setinhas vão aumentando e diminuindo de tamanho isso é por causa da variação do seno Aqui é onde o seno de x é maior aqui onde o seno de x é menor mesmo mantendo o mesmo valor de y as setinhas vão aumentando e diminuindo o
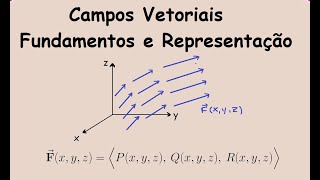
tamanho e a gente vê que quanto mais longe da origem maiores a setinhas né porque vai aumentar o valor de y e consequentemente vai aumentando o valor da setinha também que é o que tá representando a primeira coordenada do nosso vetor e além de ter Campos vetoriais no plano que é só no XY a gente também pode ter Campos vetoriais no espaço no R3 então quando a gente trabalha com x y e z e vai funcionar da mesma forma o campo vetorial no R3 vai ser uma função que para cada ponto x e y e
z vai associar um vetor um vetor que aponta para p no eixo X aponta para que no eixo Y e aponta para R no eixo k então revisando o i é associada ao eixo X o J é associada ao eixo Y e o k é associado ao eixo Z Mas ó não confunde não é porque tá no eixo X que a coordenada x que Vai comandar ele como a gente viu pode ser que o z seja a coordenada no eixo X então que seja um z envolvendo aqui a coordenada aí então por isso o ideal
é você chamar de i j e k então por isso que eu recomendo para você não confundir é quando você for falar dos pontos você falar de X Y Z então aqui é um ponto x y z com determinado coordenada x determinada Y determinado Z o vetor associado a esse ponto vai apontar em uma direção em relação aí JK então para você não confundir no vetor você pode chamar de ijk e no ponto você chama de x e y z Tá bom então isso aqui é só uma estratégia para não confundir mesmo então vamos ver
alguns exemplos de Campos vetoriais no R3 quando a gente tá no espaço esse campo aqui tá falando que para cada ponto x y z a gente vai ter um vetor que aponta para o valor de y em direção e para o valor menos dois na direção j e para o valor de X na direção k então vou finalizar aqui o que isso quer dizer aqui a gente tem x que é o que a gente chama de aqui a gente tem o y que a gente chama de j e aqui a gente tem o z que
a gente chama de k o que a gente consegue reparar primeiramente no eixo J que é esse eixo aqui a gente vê que a setinhas estão sempre apontando para a parte negativa né não tem uma setinha que tá apontando para cá em relação a esse eixo o que faz sentido já que aqui na equação dele o J tá apontando sempre para o -2 tá apontando para uma constante que é ao menos dois então realmente olhando que nesse intervalo do -2 para frente todas as setinhas vão apontar naquela direção vou apontar para o menos dois no
eixo cá que esse eixo em pé a gente vê que as setinhas vão apontando cada vez mais para cima conforme a gente vem mais para frente o que faz sentido já que no eixo cá a a gente tá com o valor de X acoplado então quanto maior o X mais para cima a gente vai apontar no eixo k e quanto menor o X mais para baixo a gente vai apontar no eixo k então quando X cresce a gente vai apontando mais e mais para cima e na direção e que a direção do eixo X a
gente vai sempre estar apontando para o valor do Y então quando o y é 3 a gente vai apontar para o três em relação ao eixo X a gente então esse aqui é o campo vetorial que a gente tá analisando nesse caso as setinhas aqui não estão com tamanho original delas o próprio software dá uma normalizada ali para a gente conseguir enxergar mas o comportamento em relação à direção e ao sentido da setinhas É esse aqui agora olha esse campo vetorial gente para cada ponto x y z a gente vai apontar para o y no
eixo I pro valor dizer no eixo j e para o valor de X no eixo k então ó a maior o valor de x mais para cima a setinha tá apontando em relação ao eixo k mais para cima ela vai estar e quanto menor o X mais para baixo ela aponta certo isso porque no eixo k a gente tá acoplado ao valor de X agora no eixo j a gente está acoplado ao valor de z e realmente ó quando o z é negativo no j a gente tá apontando para esquerda para valores negativos também e
quando Z é positivo a gente começa a apontar para direita do eixo J certo isso porque no eixo j a gente tá acoplado o valor de z e no eixo i a gente tá acoplado ao valor de y Então vai acontecer a mesma coisa ó quando Y é positivo que tá acontecendo aqui no eixo X a gente tá apontando para valor expositivos e quando Y é negativo em relação ao eixo X a gente está apontando lá para o lado negativo dele certo então vamos fazer alguns exercícios aqui gente a gente quer começar esboçando o campo
vetorial fxy que é dado por y vezes I mais meio vezes j ou seja para cada ponto x e y do Plano A gente vai ter um vetor que aponta para Y na direção horizontal e aponta para meio na direção vertical Então a gente vai desenhar para alguns pontos específicos Tá bom vamos começar com um ponto um zero no ponto um zero o nosso vetor vai apontar para zero na direção horizontal e para meio em direção vertical Então vai sempre apontar para meio aqui no eixo vertical né agora para o ponto 20 aí vai acontecer
o mesmo para todos os pontos em que o y vale zero né vai sempre apontar para zero noite horizontal e para meio no eixo vertical agora se você vier para o ponto um de X vale um Y vale um você vai ter um vetor que aponta para um no eixo horizontal e para meio no eixo vertical Então vai ser um vetor nesse formato né a ponta para um no horizontal e a ponta para meio no vertical se você vier para o ponto onde x é 1 e y é 2 você vai ter um vetor que
aponta para dois no eixo horizontal e para meio no eixo vertical Então vai ser um vetor nesse formato assim agora se você tiver no menos um um você vai ter um vetor que aponta para um no eixo horizontal e para meio no eixo vertical Então continua algo nesse formato agora vamos analisar para alguns valores negativos do Y quando Y Vale menos um por exemplo se você tiver no ponto onde X é um e y é menos um você vai ter um vetor que aponta para menos um no eixo horizontal e para meio no eixo vertical
então Como se você tivesse esse vetor aqui que aponta para -1 na horizontal e meio na vertical Mas você traz esse vetor para cá agora então vai ser algo assim quando X é zero por exemplo aqui no ponto onde X é 0 e y é -1 você vai ter um vetor que aponta para -1 no eixo horizontal e para meio no eixo vertical Então vai manter o mesmo padrão desse vetor que você tinha aqui do lado né vai ser a mesma coisa que ele então a gente pode ver que o x não interfere nesse Campo
vetorial você pode variar o x o quanto for mas quem vai realmente influenciar é o y porque só ele tá envolvido aqui né E a outra coordenada tá sempre sendo meio então esse aqui é o campo vetorial gente repara que realmente se o y for o mesmo o x pode mudar o quanto for que a setinha vai sempre ficar igual ó para essa linha de y as setinhas São Todas Iguais para essa linha de y a setinhas São Todas Iguais E aí quando Y A negativo a gente tá apontando para esquerda quando Y é positivo
a gente tá apontando para a direita agora Olha só esse exercício gente a gente quer relacionar cada um desses Campos vetoriais que a gente tem aqui com a figura correspondente Ou seja a gente quer saber cada um desses Campos Qual é a figura que tá representando eles então aqui a gente tem os campos em tamanho maior para a gente analisar cada um deles vamos começar por essa letra A vamos ver o que tá acontecendo aqui ó quando o z tá valendo zero a gente vê que o campo dele tá bem comportadinho bem estável né as
setinhas estão simplesmente apontando aqui para frente tudo certo quando você vai crescendo a gente vê que as setinhas vão apontando cada vez mais para cima em relação ao k e quando você vai diminuindo ficando negativo a gente vê que as setinhas estão apontando cada vez mais para baixo em relação ao cabo ou seja a gente já pode pensar que no eixo k Talvez ele esteja relacionado ao valor do Z Então dependendo do Z aqui a gente tá apontando mais para cima ou mais para baixo concorda a gente vê esse comportamento aqui no eixo k então
a gente pode pensar que essa figura só pode estar relacionada ou ao campo 2 ou ao campo três porque são eles que tem o z envolvido com o eixo k legal mas então como a gente sabe se é o 2 ou se é o 3 no 2 o i e o J estão relacionados ao próprio i e j e no três o i e o J estão relacionados a constantes então para o três o i e o J sempre tem que estar apontando para os mesmos valores e gente se a gente for ver ó dá
uma olhada nessa região aqui da setinhas percebeu que todas elas são muito uniformes todas elas estão muito parecidas assim como nessa região aqui então diferente do quanto a gente está variando y e do quanto a gente está variando o x a setinhas só estão mudando quando a gente varia o Z quando os Z cresce elas apontam mais para cima quando se diminui elas apontam mais para baixo ou seja no eixo Y e no eixo j a gente deve estar apontando para constantes né a gente está apontando para algo que independente do quanto x o y
e z variam vai se manter igual ou seja em relação à figura a gente só pode estar falando desse Campo três onde a gente tem uma mudança no eixo k mas o eixo i j permanecem uniformes agora vamos ver a figura B aqui a gente tem o mesmo tipo de fenômeno né no eixo k quando Z vai aumentando as setinhas vão apontando cada vez mais para cima pelo que a gente consegue notar aqui e quando você vai diminuindo as setinhas vão apontando mais para baixo não vão apontando mais para cima igual esse aqui então a
gente já sabe que no eixo k a gente também tá acoplado a variável Z então só sobraria o campo 2 aqui né Nós vamos entender em relação ao x e ao Y ó quando X tem valores negativos as setinhas estão apontando lá para a esquerda do eixo X e quando X tem valor expositivos que acontece para cá as setinhas estão apontando para parte positiva do eixo I certo então estão apontando aqui para gente Para parte positiva então no eixo e a gente deve ter alguma complemento com o valor do X com valor do x em
cada ponto e mesmo coisa no Y quando Y é positivo as setinhas estão apontando para cá para parte positiva dele e quando o y é negativo as setinhas estão apontando para o outro lado em relação ao eixo k que é o eixo do Y então todas as setinhas vão crescendo conforme o X e Y aumentam logo a gente pode relacionar o campo da figura B com Campo 2 e por fim na figura C acontece a mesma coisa quando X é positivo as setinhas estão apontando para parte positiva do eixo X quando X é negativo as
setinhas estão apontando para a parte negativa do eixo X e isso leva a gente acreditar que existe um acoplamento entre x e da mesma forma quando o y é positivo a setinhas apontam para a parte positiva do Y quando Y é negativo as setinhas apontam para a parte negativa do Y e portanto a gente leva acreditar que tem um acoplamento entre y e o eixo J em relação ao eixo k a gente vê que as setinhas estão sempre apontando para cima independente do valor de x de y elas estão sempre com um comportamento uniforme em
relação ao eixo vertical e por isso a gente pode relacionar o colocar a uma constante tá sempre apontando para o três aqui nesse caso então campo um é relacionado a figura C gente essa aula foi mais para a gente entender o que são os campos vetoriais como ele se comportam E como eles são utilizados álgebricamente graficamente Mas no geral você não vai precisar ficar desenhando as setinhas identificando cada uma delas como vai se comportar não é uma tarefa que a gente vai ver daqui para frente Tá bom então agora que a gente entendeu que são
Campos vetoriais a gente consegue partir para os assuntos das próximas aulas gente então foi isso nessa aula eu espero que vocês tenham gostado não esquece de curtir se inscreve no canal compartilha com seus amigos e já me segue lá no Instagram para ficar por dentro de tudo Tá bom então a gente se vê no próximo vídeo gente beijo [Música]
Related Videos

19:01
O que é o Campo Gradiente? | Cálculo Vetorial
Matemateca - Ester Velasquez
7,844 views

28:50
Como calcular Integrais de Linha de Campos...
Matemateca - Ester Velasquez
16,667 views

22:34
ENTENDA GRÁFICOS EM DUAS E TRÊS DIMENSÕES:...
Matemateca - Ester Velasquez
15,151 views

27:44
Visualizando e Calculando o Rotacional e o...
Matemateca - Ester Velasquez
10,252 views

27:33
UEMA 2023 Considerando a natureza ondulató...
Desvendando os Vestibulares
13 views

22:30
Parametrização de Superfícies: Visualizaçã...
Matemateca - Ester Velasquez
11,034 views

54:58
INTEGRAL DE LINHA #01✒️
Prof. MURAKAMI - MATEMÁTICA RAPIDOLA
147,928 views
21:19
Cálculo Vetorial - Campos Vetoriais (01 - ...
Prof. Dr. Diego Veras
7,603 views

12:36
CAMPO CONSERVATIVO - FUNÇÃO POTENCIAL
Prof. MURAKAMI - MATEMÁTICA RAPIDOLA
44,957 views

23:54
Entendendo o Teorema de Stokes e como util...
Matemateca - Ester Velasquez
17,464 views

25:34
Como encontrar o Plano Tangente a uma supe...
Matemateca - Ester Velasquez
5,037 views

20:48
Integrais de Linha de Campos Conservativos...
Matemateca - Ester Velasquez
10,922 views

17:54
Introdução às Funções Vetoriais: Gráficos,...
Matemateca - Ester Velasquez
22,013 views

29:10
Exercício Resolvido: Integrais de Superfíc...
Matemateca - Ester Velasquez
5,211 views

30:43
Campos Conservativos e Independência do Ca...
Matemateca - Ester Velasquez
9,315 views

21:40
Integrais Duplas: Introdução + Como calcul...
Matemateca - Ester Velasquez
55,186 views

32:39
Aula 01 Cálculo III - Campo Vetorial
Professor Douglas Maioli
43,670 views

23:42
Multiplicadores de Lagrange: Extremos com ...
Matemateca - Ester Velasquez
36,874 views

16:00
Combinação Linear de vetores: LI e LD | Ge...
Matemateca - Ester Velasquez
55,367 views

32:30
O que é o Teorema de Green e como utilizar...
Matemateca - Ester Velasquez
17,586 views