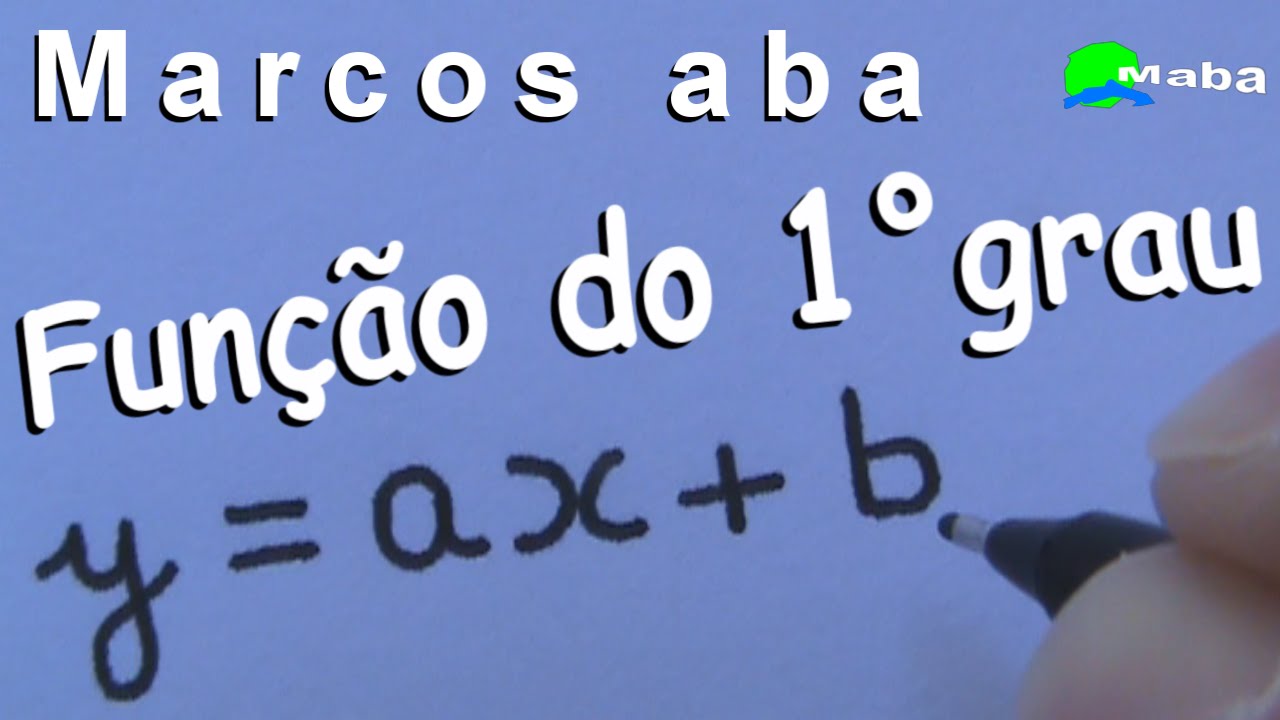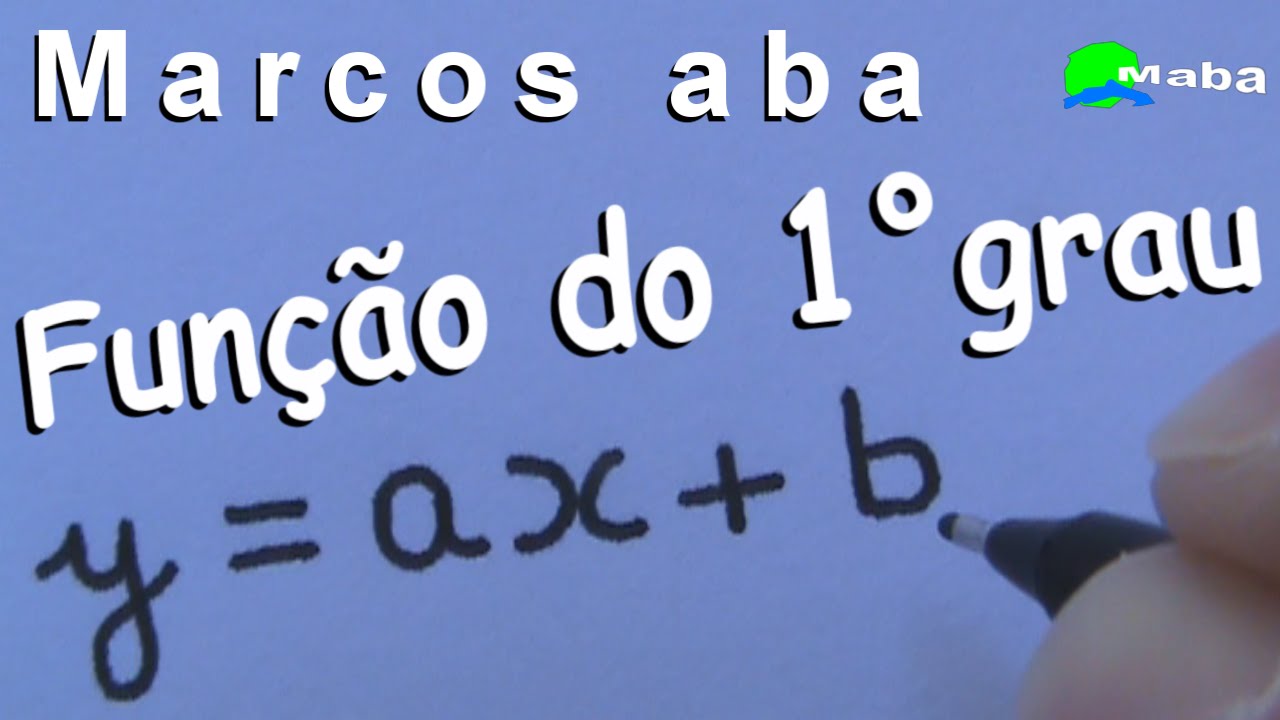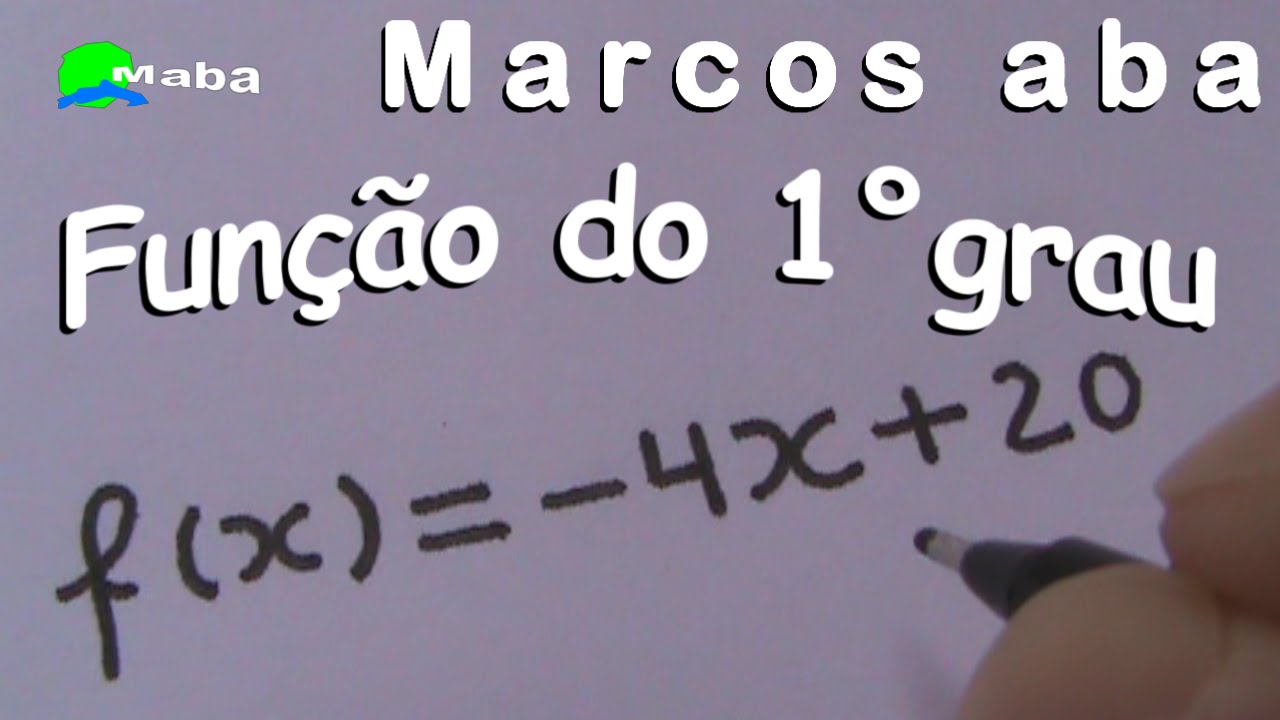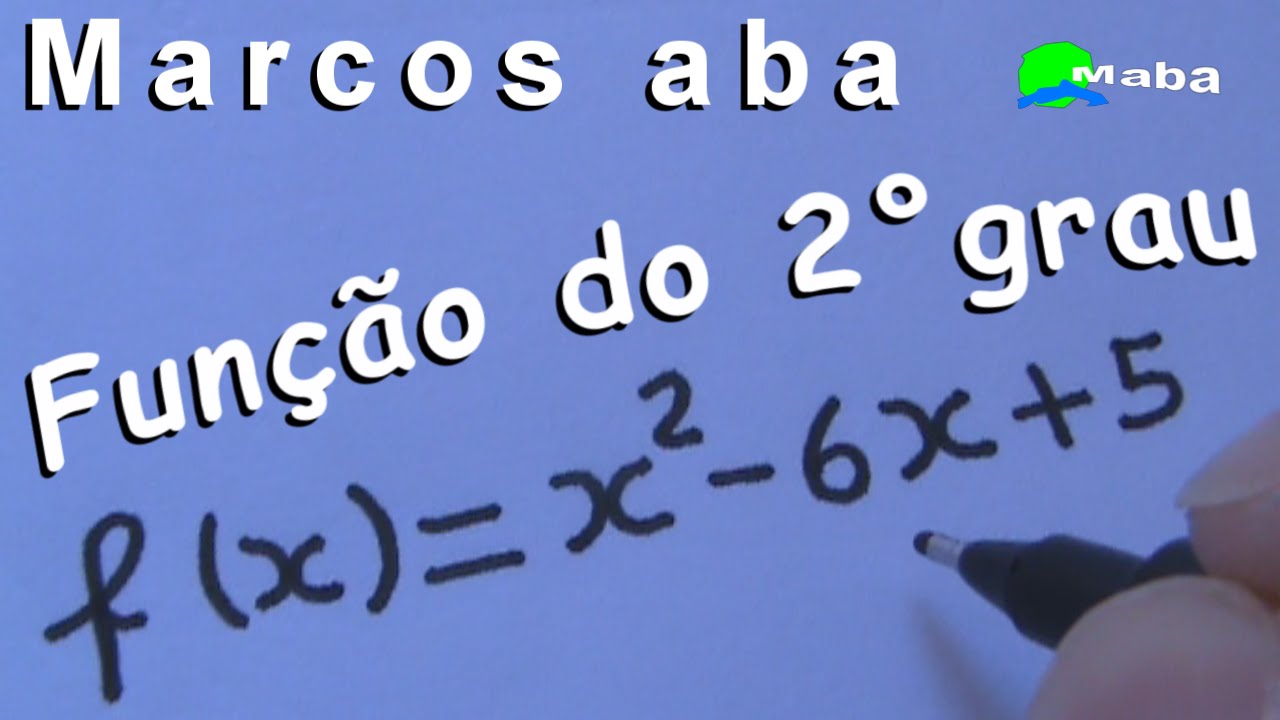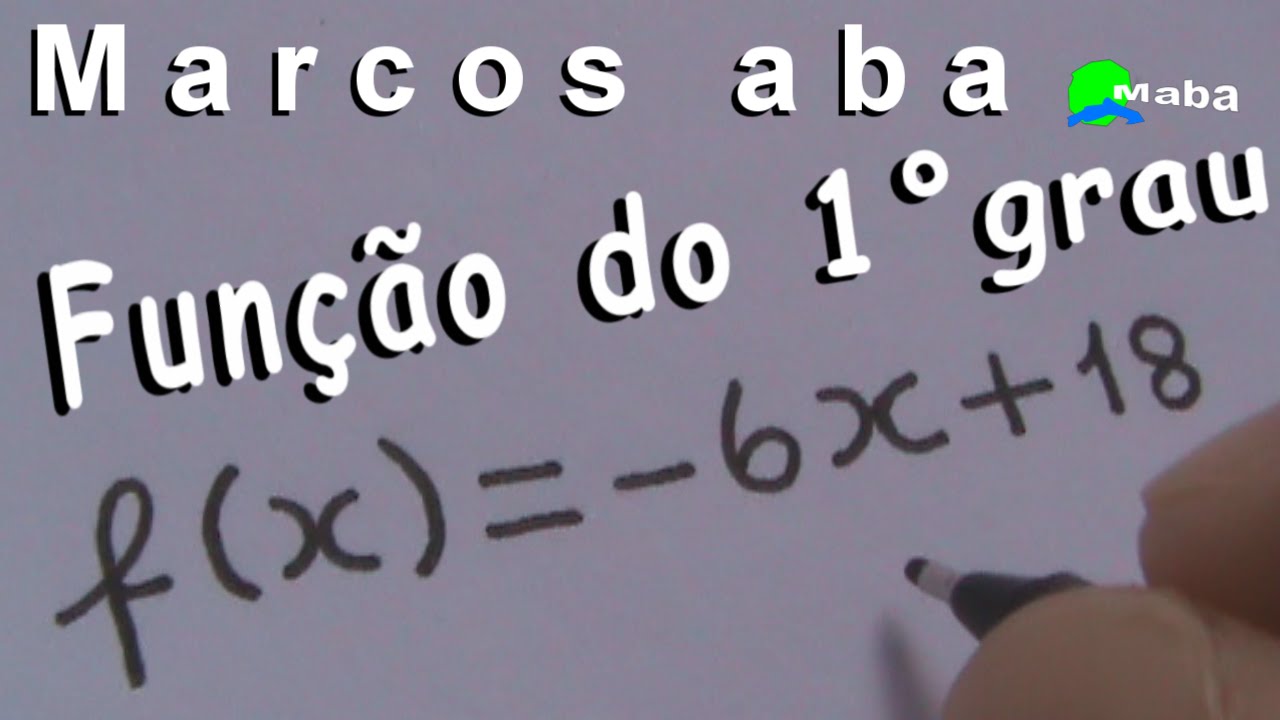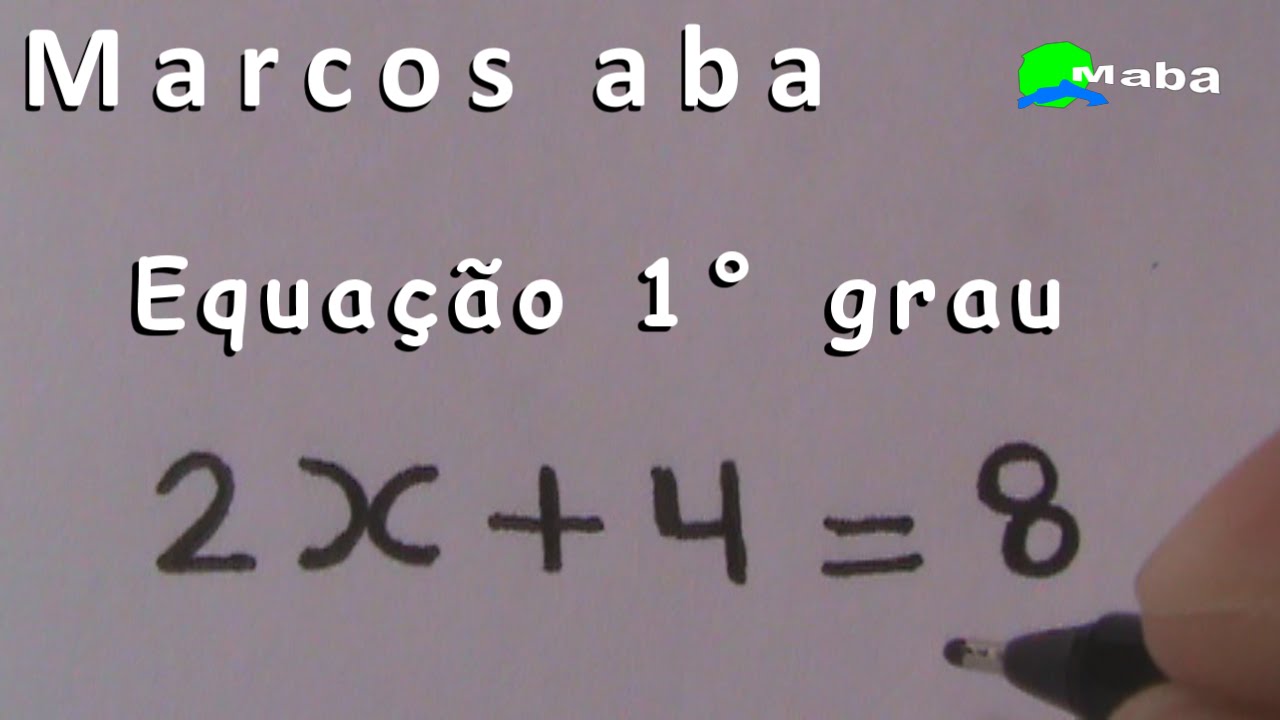Funções do primeiro grau - aula 02

Olá pessoal Marcos Aba com vocês novamente aqui no YouTube pessoal hoje a gente vai dar continuidade a aulinha sobre função do primeiro grau Hoje é aula 2 aqui está nossa função do primeiro grau que aprendemos na aula anterior né FX = a x+ b tá na aulinha passada Nós aprendemos a diferença entre função do primeiro grau do segundo grau e terceiro grau mais ou menos né aprendemos a encontrar o valor do X certo aprendemos que isso aqui um coeficiente de x esse aqui é um termo independente também chamado de coeficiente né vamos dar algumas informações

sobre o a hoje vamos dar ênfase ao gráfico e outras dicas interessantes aí que a gente vai aprender sobre a função do primeiro grau vamos começar vamos para iniciar vou mostrar para vocês aqui ó o sistema de coordenadas também chamado de sistema coordenadas cartesiano ou plano cartesiano temos aqui a reta Y né que é a reta vertical né para cima positivo para baixo negativo né reta Y reta vertical reta em pé temos aqui a reta x né que é a reta horizontal a reta deitada né chamada de X pra direita sempre positivo pra esquerda sempre

negativo né negativo pra esquerda negativo para baixo positivo pra direita e positivo para cima aqui é o ponto de origem né aonde o z o X vale z0 e o y também vale zer mas não vamos trabalhar com isso bonitinho vamos pegar apenas o eixo Y e o eixo X e trabalhar com eles Tá bom então voltando aqui pegando o eixo Y será esse eixo vertical Faça de conta que que está retinho bonitinho tá bom E aqui o eixo horizontal eixo X né e o eixo Y Então são esses dois aqui tá bom hoje vamos

dar ênfase em gráfico o que que é um gráfico por exemplo na Bolsa de Valores você tem um gráfico um dos gráficos né Mais ou menos assim ó Isso aqui é um gráfico o que que é são valores medidos ao longo do tempo então este ponto mais alto aqui por exemplo é um ponto indicado entre a reta x que vem daqui o valor e entre a reta Y que vem daqui valor então os dois se encontram aqui ó Isso aqui é um gráfico tá bom é um exemplo de gráfico um outro exemplo de gráfico seria

por exemplo na eletricidade a tomada da sua casa por exemplo exemplo a tomada da sua casa ela tem uma onda e assim chamado de senoidal né o que acontece aqui ora ela está a 110 V máximo 110 V ora está zer ora está - 110 V isso aqui também é um gráfico é o gráfico da eletricidade este ciclo completo aqui ó que forma 360º se chama senoidal tá bom e é 60 hz 60 vezes por segundo tá 60 ciclos por segundo orora 110 hora 0 hora negativo E aí vai 110 - 110 110 - 110

um outro tipo de gráfico por exemplo é o gráfico que utilizamos na parábola né que é da equação do segundo grau e função do segundo grau que é mais ou menos parecido com isso aqui ó uma parábola Onde Aqui é indicado o termo independente ó o termo independente ele indica onde vai passar no eixo Y eixo vertical e aqui embaixo em alguns casos por exemplo a parábola ela atravessa o eixo X aqui ó Então são dois pontos duas raízes a serem encontradas isso aqui também é um gráfico gráfico gráfico gráfico Marcão agora vem a pergunta

qual que é o gráfico da função do primeiro grau o gráfico da função do primeiro grau é o gráfico mais simples que existe Qual que é o gráfico da função do primeiro grau eixo Y eixo X o gráfico é é uma reta isso aqui é o gráfico da função do primeiro grau é a coisa mais simples que existe Tá bom então essa reta poderá estar aqui poderá estar aqui poderá estar aqui tá bom Ó neste sentido ó aqui o primeiro quadrante segundo terceiro quarto quadrante com com com relação à seta é sempre pra direita e

no caso aqui para cima por que para cima Ela será para cima quando o nosso a for diferente de zero Ou seja quando o a for maior que zero ou A positivo tá bom co serão várias retas não é apenas uma reta O que que a gente vai encontrar a gente vai encontrar o valor no eixo Y e o valor no eixo X e quando o a for menor que zero o a for menor que zero como que fica então vamos fazer aqui a reta horizontal a reta vertical né quando ele for menor que zero

então a reta ficará neste sentido aqui ó pra direita também Porém para baixo agora porque o a é menor que zero tá vendo Então a reta ficará neste sentido aqui ó sentido do quarto quadrante primeiro segundo terceiro quarto quadrante então aqui no caso o a ele é diferente de zero no entanto o a ele é menor que zero sempre que o a for menor que zero a reta será para baixo aqui ó todos pra direita Porém para baixo com relação ao eixo Y aqui né o eixo vertical tá vendo ó a menor que 0 para

baixo a maior que zer para cima marcou só existem estas duas posições só essas duas posições tá bom para cá não conta porque para cá é negativo ó para lá é negativo também então é sempre pra direita A positivo e a negativo agora vamos a algumas informações sobre o a Vamos colocar aqui ó FX = a x + b este a aqui ó e Existem algumas informações sobre ele o nome dele é coeficiente nós já aprendemos o nome dele certo é coeficiente angular que eu já vou explicar para vocês por angular outra coisa e uma

informação já foi né Qual que é a outra informação o a jamais pode ser zero Por que Marcão que o a jamais pode ser zero imagina que você coloque um zero aqui no lugar do A então vamos lá FX é igual 0 ou 0 x + b ó o a agora é 0 o que acontece aqui ó 0 x x 0 vezes qualquer coisa é 0 Você acaba de eliminar a função do primeiro grau mas como assim Marcão que você acabou de anular a função do primeiro grau porque ó para termos uma função do primeiro

grau temos que ter pelo menos um X e 0 x x você elimina o x fica 0 né 0 vezes qualquer coisa é 0 então não existe mais a função no primeiro grau apenas o termo independente que é chamado também de constante Tá bom então dando valor aqui ó FX é igual a 0x + 3 o que acontece esse aqui é eliminado então fica só constante E aí Alguns costumam chamar de função constante O que seria uma função constante é uma função onde não há o x h apenas o b aqui ó o ou seja

o y será igual ao B este será o valor do Y no caso 3 então a gente conta TRS como é positivo 1 2 3 e a reta passará aqui ó deitada Tá bom então será uma função constante aqui no caso FX ou Y né FX = 3 Tá e isso aqui não é uma função do primeiro grau porque função do primeiro grau o gráfico é uma reta meio que oblíqua assim né meio deitada né com relação a esses dois aqui que estão perpendiculares né eixo X e eixo Y que formamos 90º aqui 90 aqui

90 aqui e 90 aqui 360 total né então agora então essa foi mais uma informação sobre o a o a jamais pode ser zero o a é diferente de zero tá bom qual que é a outra informação sobre o a a outra informação é o seguinte ele é chamado de coeficiente angular Por que coeficiente angular porque é o seguinte Dependendo do valor dele por exemplo vamos traçar aqui um gráfico Dependendo do valor dele vamos supor que o nosso B seja iG 0 B = 0 o b a reta passa bem aqui nesse meio Zinho aqui

ó bem no 0 do x 0 z0 do Y eu vou explicar isso mais paraa frente aí o que acontece o a Dependendo do valor do a vamos supor que o a seja um valor qualquer Por exemplo agora eu vou dar um valor o a será igual a 9 o a tendo o valor de 9 a nossa reta ficará mais ou menos aqui ó tá então o que acontece ele forma um ângulo aqui um ângulo maior e um ângulo menor aqui ó por isso que ele é chamado de coeficiente angular mudando o valor dele por

exemplo Vamos diminuir o valor era 9 agora vamos fazer o a iG A1 o a = A1 por exemplo a reta ficará certinho aqui ó o a = 1 temos 45° aqui e 45º aqui ó então você vê que ele é um coeficiente angular Porque dependendo do valor dele ele muda o ângulo aqui ó da reta Vamos diminuir o valor vamos vamos diminuir esse valor por exemplo para zer para 0,2 aqui ó com a valendo 0,2 a nossa reta ficaria mais ou menos aqui ó você vê um ângulo bem fechadinho aqui um ângulo bem maior

aqui e E se o a for igual a z0 por exemplo teremos aqui a reta ficará aqui em cima ó Isso se o nosso B for zero né então a reta ficará aqui em cima ó o a = 0 e se o a inverter o a for menor que zero vamos passar aqui para um um outro valor aqui por exemplo menos o men-1 vai Então temos aqui o eixo ag o eixo X o eixo Y A nossa reta agora ela começa a descer o -1 por exemplo seria o contrário agora el fica para cá ó

45º aqui 45º aqui nesse caso o a vale é igual a -1 então é por isso que ele se chama coeficiente angular Porque dependendo do valor dele ele terá um tipo de reta e sabemos que a reta Quando está para cima o a é positivo A positivo aqui o a anula né o a = 0 e aqui o a negativo ó -1 a reta está para baixo por isso que ele se chama coeficiente angular tá Tá bom Agora vamos trabalhar um pouquinho com o FX em relação ao gráfico e aqui está FX = 4x +

8 bom vamos formar o gráfico em primeiro lugar como que a gente faz para encontrar o valor de X nós trocamos nós igualamos o FX a 0 aprendemos na aulinha anterior tá bom o FX também é chamado D Y né então nós passamos o Y para z0 isso aqui que também é isso né Y = 4x + 8 e para encontrarmos o valor de X basta trocar isso aqui por um zero então 0 ig a 4x + 8 né que que a gente faz agora passa o 4x para cá ou mais 8 para cá vamos

passar a + 8 então ficará 0 + 8 passando para cá do sinal de igual fica -8 é igual quem que ficou do lado de lá o 4x aqui está e o que nós temos aqui agora 0 - 8 0 não é nada né então ficou apenas o -8 aqui ó zero não considera para nada então -8 é ig a 4x que que temos agora temos que encontrar o valor do X né aqui por exemplo é 4x = -8 eu não quero saber o valor de 4x eu quero saber o valor de X então vamos

jogar este número para cá então Olha só vamos jogar esse quat para cá né ele está multiplicando ali jogando pro lado de cá do sinal de igual ele passa dividindo ele inverte tá multiplicando o contrário da multiplicação é a divisão então vamos passar para cá vai ficar -8 so 4 então -8 so 4 é igual ao valor de X temos aqui embaixo o mais do 4 né então é o seguinte menos dividido por mais é menos conforme a regrinha de sinais que eu ensinei a vocês né menos dividido por mais é menos esquece os sinais

agora os números agora 8 di 4 = 2 então -2 = x ou seja o valor deste X é -2 né x = -2 Marcos o que que é esse -2 esse -2 aqui ó é o valor que o x terá na reta Então vamos traçar o gráfico aqui ó então aqui está a reta x e temos aqui a reta Y né então o X = -2 então você pode colocar aqui ó para esquerda sempre negativo né aqui no meio é chamado de ponto de origem é o zero do Y e o zer do X

Este é o eixo X e este é o eixo Y Então -2 a gente vai colocar para cá então -1 - 2 aqui está - 2 então é o valor do X o valor do X que você encontrar é o valor que você vai colocar na reta x Marcos para nós encontrarmos o valor do X nós igualamos o y a 0 este Y aqui por acaso é este Y exatamente que que nós fizemos vamos supor que o valor estaria aqui ó vamos descer ele para zero ou seja para este ponto se ele estiver negativo vamos

aumentá-lo para zero ó aqui ó será Zerado ele estará bem no eixo X isso que é o y = z0 que é o caso que está aqui ó nós trouxemos o Y para zer trouxemos para cá então quando o y Vale 0 o x Vale -2 tá aqui ó então aqui é a junção do X com Y então podemos colocar até aqui uma marca aqui ó que a junção dos dois estará aqui porque o y estará 0 e o x estará -2 que acabamos de encontrar o valor dele tá bom ótimo então já encontramos o

x do nosso gráfico Lembrando que o gráfico da função do primeiro grau é uma reta não é nada mais que uma reta né então já encontramos um ponto aonde a nossa reta irá passar certo agora eu pergunto para você esta reta ficará neste sentido daqui para lá ou ficará neste sentido aqui ó neste sentido e por que ficará neste sentido porque o a é positivo ó o a é maior que zero é positivo então a reta ficará neste sentido agora eu não sei se ela ficará assim assim assim ou assim depende do valor do Y

que é este valor aqui ó que é o f Dex aqui também é chamado de F Dex Então dependendo do valor do y a reta ficará em uma posição agora para nós traçarmos para nós encontrarmos o ponto que será do zero para cima no Y temos que encontrar o valor do Y como fazer para encontrar o valor do Y olha só para nós encontrarmos o valor do X nós trocamos o Y por 0 ou seja nós zeramos o y nós anulamos o y trouxemos para zero e para encontrarmos o valor do Y agora adivinha vamos

zerar o x ou seja vamos supor que o valor é -2 vamos trazer para zer vamos levar para zer vamos supor que ele é mais alguma coisa mais 7 vamos trazer para zero e trazer o X para zer o que que é é colocar um zero no lugar dele da mesma forma que o y é só colocar um zero no lugar dele vamos fazer isso vamos então o y continua ou Fx né então vamos colocar aqui ó Y aqui já é uma outra coisa né então Y é igual qual que é a nossa função do

primeiro grau Esta é a função inha do primeiro grau que está levando a este gráfico não se esqueça hein então o FX ou Y é = 4x + 8 Então vamos colocar aqui 4x + 8 para encontrarmos o valor de y devemos igualar o x a z0 trazer pro ponto de origem então y é igual a 4 aqui está multiplicando né então vai ser a 4 vezes quem 4 x 0 porque agora vamos encontrar o y mais 8 e o que que a gente está fazendo aqui olha só 4 x 0 = 0 qualquer coisa

vezes 0 é 0 nós acabamos de trazer o X para 0 anulamos o x e ficamos com mais 8 Então y é igual 4 x 0 é 0 + 8 0 + 8 é apenas o 8 né que não é nada então Y ig a + 8 + 8 e 8 é a mesma coisa então o que que a gente fez a gente igualou o x a 0 encontramos o valor do Y Marcos uma pergunta eu percebi que o y é igual ao b o valor do B que é o o Ax + B né

FX Vamos colocar aqui ó FX = Ax + B eu percebi que o o Y ou Fx É iG B aqui ó Y iG b o valor do B + 8 exatamente Então já guarda isso daí ó o b ele é o valor que a nossa reta ele é o valor o b é o nosso valor em que a reta irá tocar o eixo Y no caso o + 8 aqui já estava indicando então o 8 é o ponto onde vai ser tocado a nossa reta Y eu só igualei a zero aqui para vocês perceberem

aqui ó então o y será toado no 8 onde está o b normalmente o b indica onde a reta y será tocada então aqui a gente vai encontrar o 8 então Y ig a 8 né que é este 8 aqui ó Então vamos contar aqui ó 1 2 3 4 5 6 7 8 Então será aqui ó então quando o nosso x vier a 0 ele ficará aqui o nosso Y valerá o o tá ali ó que acabamos de encontrar Então a nossa reta ficará neste sentido aqui ó tá vendo o nosso coeficiente angular que

é o azinho ele foi positivo então fica dará uma uma reta neste sentido aqui tá bom esta este eixo vertical aqui poderia ser maior não há problema nenhum qualquer tamanho Então temos aqui uma o nosso gráfico da função do primeiro grau tá bom aprendemos mais um pouquinho aí tá bom pessoal então o que que aprendemos aqui a encontrar o valor de x que já havíamos aprendido colocamos aqui no gráfico né no caso -2 para que isso aconteça o y deverá ser zero é só colocar um zero no lugar dele não há segredo nenhum E aí

encontramos o men2 que é o valor do X uma outra dica aqui ó alguns professores chamam o X Ele contém três nomes guarda isso aí o X Ele é chamado de raiz da função o o nome dele é raiz da função por quê encontre o valor da raiz da função ou seja o valorzinho do X que nós encontramos aqui ó em outro caso ele é chamado de zero da função ele também é chamado de zero da função só que o valor dele não será zero para encontrarmos o zero da função ou seja o x quem

deverá ser zero é o y Hum uma dica importantíssima o X é ch chamado de zero da função é apenas o nome dele que é zero da função ele terá um valor quem será Zero no ato em que o x chamará zero E terá um valor quem estará com valor de zero é o y porque trouxemos ele para zero aqui ó então isso aqui é o X é o zero da função e a raiz da função também o zero da função é igual a -2 e quando que ele é zero quando que ele é o

zero da função quando você encontra o valor dele quando o y é igual a 0 Tá bom então vamos parar por aqui na aulinha seguinte a gente eh treina um pouquinho mais com mais dicas e vamos fazer mais gráficos tá bom Por favor se você gostou clique no joia se inscreva compartilhe deixe um comentário não estou conseguindo responder a todos e uma coisa muito importante alguns alunos estão deixando comentários mas não há a possibilidade de resposta Olha só Nesta aula aqui por exemplo temos algumas respostas este Aluno por exemplo não há resposta neste outro outro

caso aqui ó esta Nesta aula aqui esta aluna aqui ó não tem direito de resposta eu não sei se é porque vocês estão usando tablet celular ou o que que é então é isso aí pessoal Marcos Aba aqui no YouTube com vocês novamente eu espero vocês pra próxima aula um abraço Marcos Aba aqui no YouTube com vocês [Música] novamente [Música] n