Projeto e Análise de Algoritmos - Aula 01 - Introdução ao projeto e análise de algoritmos

[Música] Hola pesoal sean benvidos a nosa primera aula de análisis proyecto y análisis de algoritmos n Esa primera aula vamos a presentar algunos conceptos introductorios para disciplina apres presentaremos algun conitos como que algoritmo o que que un problema o que una instancia y apr presentaremos también comoera de correción de algoritmo y como medir consumo de tiempo de un algoritmo así como acontece con engeros civ el tcnicas y algas mtricas que usan para prever comportamento estruturas antes de construirlas asim comoes elesen nos tambén como engeros da computación a gente precisa prever como que será comportamento de

un algoritmo antes de implementarlo esa disciplina nos ayudar aer exatamente ISO ent primero vamos ver alguns conceitos importantes para para poder traballar yer anális su algoritmos primero precisamos definir o que que un algoritmo un algoritmo un procedimiento computacional que está bien definido que recebe algun valores como entrada y producir dar como resposta alg valores como saída otra defini simples ferr para resol problemas computacion un algoritmo res un problema y que un problema un problema definido por una descrición parámetros tanto de entrada como de saída una descrición sobre propriedades que a resposta de satisfer y o

que que una instancia una instancia de un problema eh se obt a fixar alguns valores a fixar verdad valores para todos os parmetros problema de aquí a pqu vamos ver un exemplo aquí temos un exemplo vamos suos un problema de ordenar una secia de elementos a1 a2 at a Y esa secia que ser ordenada de manea crescente precisamos definir con que ser entrada son saídas como que ser a saída y cu propriedades que esa saída de cumprir a entrada esa secia a1 a2 a n cu que a saída a saída tamb secia a L A

l a L que cumpre seguintes propriedades esa secia permut secia original certo permuta t que a un l se menor que a do L y así sucesivamente y todasas se menor que a n l aquí un exemplo decia acia de entrada por exemplo sera secia aquí 10544 y a segda sería secuencia ordenada de manea crescente 4 5 10 20 40 nesta disciplina vamos ver varias formas Deer ISO de ordenar una secuencia de elementos aquí temos un otro exemplo eh de problema o problema o seguinte encontrar o camino mínimo desde un punto inicial at un punto

final certo ent cualqu entrada entrada entrada ser por exemplo coordenadas punto inicial y coordenadas de es punto final y que serda saída ser cam que mea desde pto inicial atto final y al propedades esam de ser mínimo disciplina también vamos ver alg algoritmos que per res es problema problema cam mínimo por exemplo usando grafos cuando a gente proyet un algoritmo primero queos que ver es si algoritmo está correto un algoritmo correo si resolve problema para toda instancia de entrada o algoritmo termina característica importante que algoritmo termine no fi infinitamente un Loop intermin y produz saída

que satisf propiedades que for definidas para problema Ah primero paso es demostrar si algoritmo está correcto si f o que promete para Fer a proba de correción algoritmo existen algumas técnicas cuando estamos trabando con un algoritmo interativo que usa lazos usada a técnica de invariante do lazos o que que un invariante dos lazos una propriedad que debe ser verdadeira antes durante y após execu do lazo usando ISO a gentee mostrar provar que algoritmo está correto no caso de algoritmos interativos no caso de algoritmos recursivos usada a técnica de inducción matemática eho instas veremos de aquí

a un exemplo fechamos ese exemplo de algoritmo un algoritmo simples que Calcula un máximo de una secuencia a gente decidió un algoritmo recursivo poderíamos feo un algoritmo interativo también que que ent recebe como parámetro un vector a deo n y encontrar cu que máximo Dee vector si n igual a un o se sio de vector un ent ya que un máximo prio elemento que único que está n vector que sería caso contrario a gente Lamar recursivamente algoritmo para calcular que máximo vector a con n men Un elementos o se desde posición un posición n men

ent es ese método de aquí calcular que máximo desde de a desde 1 n yver un valor que valor x certo aquí aquí ya valor má máximo de un vector de un a tn men 1 cuando obtiver ese valor único que ficara para resolver es perguntar si ese máximo encontrado es mayor a un elemento que está faltando que sería o a posición n si mayor a posición n ent qui un mayor es x caso contrario un mayor e a de Okay ya Pro estamos o noso algoritmo o próximo paso verificar se algoritmo está correto estamos

vendo que un algoritmo recursivo ent vamos usar a técnica de inducción matemática noo que sería n para demostrar que algoritmo está correcto ent Cómo que usamos esa técnica primero falamos si algoritmo está correcto para un instancia pequena n ese caso para nahu después asumimos para una instancia de tamaño n men verificamos si está correcta y despu mostramos para n si que debeer ent vamos ver pasos para demar cor algoritmo máximo si n ig 1 Vamos ver algoritmo dev a respa correta si n ig 1 sí un elemento devolve a dev resposta correta s por hipótesis

a supor que para n mayor igual a do o algoritmo a llamada máximo con un parámetro a y n - 1 produ un resultado esperado pues n - 1 es menor a n Enton supondo que esa Lía de aquí Me devolve resultado correcto me devolve realmente cu que máximo de vector a desde posición atn - 1 tambo Mostrar agora que o algoritmo está correcto cóm ent H aquí a gente ya sabe que me devolve a respesta respuesta correcta para un vector de un atn men 1 considerando ISO vamos ver si lneas cuat a se calculan

correctamente un máximo vector a de 1 n supondo que un x Está correcto que un máximo de un atn men 1 único que estaría faltando ver a última posición vector mayor menor que xo exatamente que estamos l cer cono demra que algoritmo realment está coro desp de ver algoritmo Está correcto próximo paso calcular que cons para vamos estimar cuá tempo a máquina gastar o cu de memoria será necesar para resolver una instancia de problema forma simples deero ser simplesmente colocar colocar algoritmo no inicio y colocar que peg horario de inicio horario de yer a diferen

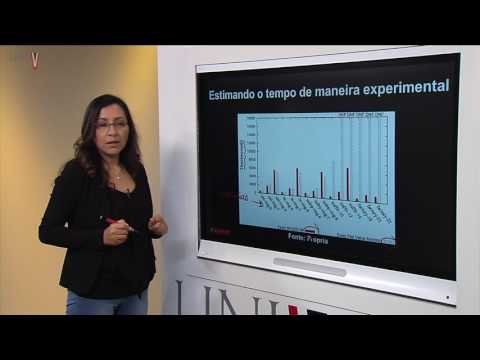
no prio programa vamos estimar tempo de manea experimental vamos suos aquí do algoros ese verm y ese otro aquí de ponchos son do algoritmos que resolv un mismo problema aquí est mostrando tempo que demora para resolver varias instancias aquí instancias varias instancias yo es do algoritmos est mostrando aquí tempo que cons vemos Que o vermelin consue resolver todos problemas todas instancias desp todas instancias ese problema enant de punos ve no consue resolver problema noo máximo determinado aquí significa que no terminó did not Finish DEA forma veces comparamos algoritmos de manea experimental a gentea de saber

cuor que real cons enmos de entrada es de aquí de manea experimental simples veamos novamente pas de para problema de ordena queremos ordenar un vector a de una n de manea crescente y no entrada esencia de números 23 21 28 etc y a saída acia ordenada certo vamos ver primero agora o algoritmo de ordenación por inser o que que y para eso vamos Mostrar como que funciona con una instancia en particular eh posición J en algú momento algoritmo de ordenación por inser que que posición J men Un vectores ordenado si vedes observan aquí toda esa

parte en amarelo está ordenada está y vamos tentar inserir toda esa parte aquí no está ordenada Vamos tentar inserir o valor que está posición J no lugar certo eso de aquí ese elemento que deseamos inserir no lugar certo ISO o que o algoritmo que tenter o algoritmo de ordena por inser por eso que se Chama de inser porque tenta inserir un elemento no lugar certo c vamos guardar esa posición eh ese valor verd Chave esa vari Chave est guardando es2 que desira parte vor y guardamos vari Chave Okay aquí estamos como un problema que queremos

resolver que que vamos que2 queer colar lugar certo Okay o que queos vamos ir comparando con todos elementos y empurrando elementos que son mayores a vamos perguntar aave mayor que no emp elemento yamos vamos comparar con7 a que2 mayor que7 no emp con3 aave mayor que 23 no amos con 21 aave que 22 mayor que 21 samos empar elementos y colamos lug y cer O 22 lugar certo y que queora noo parte vector ordenado yotra parte vector que no está ordenado certo yora mmo proco para próximo elemento que serí 25 colocamos ji jalando a posición

posición está elemento 2 guardamos 25 variável Chave y vamos tentar o mesmo yos mesmas perguntas a Chave mayor que 28 no empur aave mayor 27 no emp aave mayor que 23 ent 25i certo se aquí cu que proco que a gente a gente está comparando 25 con todos elementos que est antes del y empurrando elementos que son mayores no pior dos casos a gente que empurrar todos es elementos que est aquí certo y ahí continuamos agora queos parte vector ordenado continuamos con próximo elemento que ser colocar o 24 no lugar certo y agora vamos o

mesmo con 24 empur 2 empur 2 empur 25 pergamos si aave mayor que 23 no os 24 lugar certo de noos agora parte que está ordenada está faltando 29 o 29 ahos o mesmo pergamos con cada un elementos not que seos n elementos a gente prisar no pior casos vamos que aquí temos elemento no lugar de 2os noor casos a gente que empurrar n - 1 elementos certo es importante notar depois para anális algoritmo n caso a gente no preciser nada porque femos apenas pergunta o 29 mayor que 28 s ent coloca posición y+ pronto

y acabó finalmente vetor ordenado completamente desde posición posición n Aquí está pudo algoritmo ordena por ehos aquí ent rece como parmetro vector y n que sero vector estamos trando con vectores desde n importante notaro parición do atn que ir guardando Chave elemento que desar lugar certo esa parte de aquí cu se queer perguntar aave mayor que elemento posición y seave mayor empurrando elementos es de aquí Ur elementos que simula con es inst y final cuandoo no se verd aoca aave posición yto es aquí algoritmo de ordena por inser test ese algoritmo no verdad se joda

ese algoritmo o pensa Cuántas veces son feitas voy botar un poquillo aquí Cuántas Cuántas compara es algoritmo que compara compara aquí aquí y aquí si por exemplo garía de contar Cuántas compares algoritmo a podería ese gráfico aquí eh aquí para un vector deño n de uno n fixo un suor deo eh 60 cuas compara realiza algoritmo anterior a gente poder rodar con instancias diferentes claro de mesmo 60 un número de compara a conta de algo número de compara a encontrar por exemplo de aquí que aquí a gente no para un problema deo 40 por exemplo

60 para unmo un número de compar diferente aquí gente aquí pior caso y también un mellor caso que sería es de aquí cierto y también teng un caso medio medo mesmo para una instancia mesmo comportamentos verdad un número de comparaciones diferentes a gente podería medir otras cosas por exemplo no somente un número de podería ser un número de atribui en número de linas que son executadas os varias formas de medir cu que consumo deo algoritmo vamos que queremos contar un número máximo de atribu número máximo de atribu que atribu aquí aquí aquí aquí noer atribu

aquí atribu aquí tamb y aquí tambén vamos contar cuas que número máx de algoritmo eh es de aquí es prima lerri verd por que n n para contaras atrion aquí men do má ser número de atri que certo que cont que má para pod aquí má que igual a n a gente está contando atribu por atribui que trab cuantas atribu doer menos que l un a do a TR men atribu cuas atribu cuero yora es par de aquí importante Cuántas ve empurra aquí Cuántas atribu son feitas aquí que enas palas sertas ve que empurra elemento

no pior casos a a máxima cuantidad quee empurrar ser que vi exemp que para último elemento pior casos podería empurrar n-1 elementos certo ahí pueder n-2 etc etc y para posiciones iniciales vaer do y 1 no máximo eso de aquí dar que eh n por n 1 sobre 2 es somatoria eh da es resultado o mesmo acontecer cona se y depois a L s ser o mesmo que a L do 3 que n - 1 se a gente a somat deo ISO o resultado ser n 3n - 3 número máximo de atribu menor ig n

3n - 3 not que a gente un cálculo a atribu que for realizad pens en Consumo de de consumo de tempo por cada l de ex a gente contar Cuántas ve executada cada l considerando que cada l cons unid deo vamos contaro esa l de aquí ser ex n ve de aquí ser n ve n n a sa que n tamb y a ser desp vamos pasor a c y a que vies n n etc etc certo [Música] aer ve a porque que verificar má ve para poro que aquí má considerando c aquí ser do

finala deoo dar ese total de aquí 3n mán -8 porora estamos calculando cu que cons considerando que cada l cons unid deo eh tambén podemos considerar ser má detal aí y considerar que cadaa y de có consum unidades de tiempo Cada deas consum unidades de tiempo diferente ISO aar n expr no Mostrar como que feo es cálculo multiplicar cada cada un valores que tamos slide anterior por no final vamos expr tipo ser expr C2 n c1 c en que C2 c y C constantes Que depend ti verdad a gente varos cálculos diferentes formas de calcular

o consumo de tempo de algoritmo cuando calculamos número de atribui chegamos n ese result cuando consideramos que amos computar todas linas que foron executadas no algoritmo considerando que cada una consume una unidad de tempo lamos n ese resultado y cuando consideramos que cada una consume ti unidades de tempo lamos n otro resultado má será que para un n Grand diferencia Fer una contag t deter esa de aquí muo má detal será que diferen a gente Vero de aquí a ent n noas análises vamos ficar satisfeitos anális má aproximadas pretendemos medir apenas a ordem de grandeza

función de tempo algoritmo cu consum algoritmo Queremos saber para n grandes parao vamos introducir alguns conitos que son n ese caso anotación o teta y ega o oma y teta es conitos será apresentados Noa próxima aula ent espero quean gostado de esa aula y no percan a nua aula número [Música] do [Música] [Música] [Música] ah [Música] Oh