Cálculo I - Aula 28 (3/3) Exemplo com frações parciais; Volumes
7.6k views4298 WordsCopy TextShare
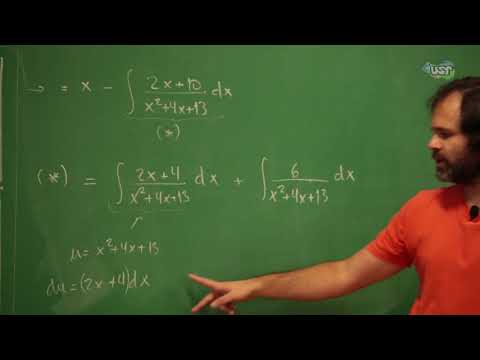
Canal USP
▶ Este é o curso de Cálculo Diferencial e Integral I oferecido pelo Instituto de Matemática e Estatí...
Video Transcript:
[Música] do primeiro para o segundo não tem um grande salto na via com o que se percebe que raízes simples do poli nome vão gerar fatores na primitiva que vão te ver com eliene desse cara as duplas vão aparecer fatores desse tipo raízes tripas vão aparecer o caso ao quadrado etc o que fica um pouquinho mais chato é o caso quando você tem coisas irredutíveis vamos pensar nesse exemplo aqui ó x ao quadrado mais 2 x + 3 / x ao quadrado mais 4 x mais 13 quase um exemplo aleatórios dois planos de grau 2
como é que faz seu grau é igual dá para dividir então vai dividir x ao quadrado mais 2 x + 3 / x quadrado mais 4 x mais 13 o que você espera que dê uma constante como divisor o resto um plano de grau 1 não pode ser um resto pode ser zero porque obviamente esses problemas não são últimos 12 ou 13 porque se fosse também um exercício muito fácil cancela sob uma constante tchau então aqui vai ficar 1 eu vou ter menos x quadrado - 4 x menos 13 que vai te dar 6 x
mas é aqui é mais tão menos 10 os dois ou mais aqui fica menos 2 x menos 10 é isso esse é o resto né e portanto essa primitiva aqui como é que fica vamos escrever mais uma vez justamente ele x ao quadrado mais 2 x + 3 eu consigo escrever como sendo uma vez x ao quadrado mais 4 x mais 13 mas o resto que é quanto menos 2 x menos 10 na hora que eu divido tudo o x quadrado mais 4 x mais 13 o que vai ser esse cara cancela vai ficar 1
- 2 x mais 10 sobre x ao quadrado mais 4 x mais 13 não tem duas primitivas para calcular eu vou calcular as duas né essa aqui é muito fácil mas tem que fazer também então esse cara aqui vai virar o que né ele vai ficar x - a primitiva de 2 x mais 10 sobre x quadrado mais 4 x mais treze pb x então esse cara que a gente precisa calcular também pergunta o que dá pra fazer alguma coisa com ele esse povo não por nome o irredutível neves e calcular o delta você vê
que não tem raiz ok você não pode não é redutível que a gente sabia que na decomposição via frações parciais e aparecer o que um cara de grau um morador dele eu preciso fazer essa conta não jataí já têm um cada degrau então esse exercício para mostrar como você lida com carinho desse tipo aqui tá e como é que se lida com carinho desse tipo a o de baixo o que ele é x ao quadrado mais 4 x mais 13 ele tem a ver com a derivada de cima quase na qual é a derivada do
denominador 2x mais quatro aqui eu tenho 2 x + 4 se forçar a barra se enxerga lá dentro né o numerador é 2x mais quatro mais seis tá bom então vou poder escrever isso aqui né essa é a graça quando você tem um cara de grau dois aqui embaixo a derivada dele vai ser o que um cara de grau 1 a mais e multiplica e some subtrai coeficientes pra sempre dá pra fazer isso é importante é um cara de grau dois aqui embaixo do elevado vai ser um termo de grau 1 a 1 então eu
posso multiplicar por constantes para ajeitar o termo linear para ficar igual e são mais subtrai constantes depois para que o termo constante fica igual também tá então nesse caso como ja ta 2x é que fosse 3 o que quer fazer o que eu faria multiplica por dois terços multipliquem dividir por dois textos que dá certo não precisa nesse caso não precisa então esse cara que eu posso escrever como sendo 2 x + 4 sobre x ao quadrado mais 4 x mais 13 deixei mais primitiva de 6 x ao quadrado claro pra todo mundo que qual
foi a passagem que eu fiz porque eu fiz a conta desse jeito sim está também muito bem desse jeito tem uma das parcelas é que é muito fácil de calcular qual delas a primeira porque a primeira é um consciente onde o numerador é derivada do denominador enquanto que dá uma primitiva desse tipo vai aparecer um blog ou você depois de muita prática seja sob qual é com o que têm que fazer senão qual que é o jeito o padrão para resolver esse cara aqui vamos chamar nessa parcela aqui né vou fazer o que gostes ao
quadrado mais 4 x mais 13 quem vai ser o meu tá tudo feito de caso pensado pra essa separação 2x mais 10 desse jeito foi de caso pensado para acontecer exatamente isso tá bom então essa primeira parcela vai ficar o que a primitiva de che é 2x mais quatro de x é o de um e esse cara que é o mais a primitiva que ficou faltando ali que é o pedacinho vão dizer que tem alguma novidade então o que vai te dar isso lm do módulo de o quinto módulo de 11 x quadrado mais 4
x + 13 + essa primitiva aí tudo bem certo jóia pergunta se você quiser ser muito minucioso uma coisa é necessário esse módulo aqui não porque se tornou um problema de grau dois e irredutível portanto ele nunca troca de sinal e nunca troca de sinal e no zero ele vale 13 quer dizer que ele é sempre positivo você quiser sentir esse mundo não é necessário também ok que sobrou então para calcular esse cara aqui que eu vou chamar de duas estrelas como é que o calcula primitiva de uma constante por um polígono de grau dois
é irredutível a constante pode sair rock então se você quiser esse cara vai ficar seis vezes a primitiva de the x o que você precisa fazer uma coisa de novo é tudo de caso pensado né a gente usa uma técnica que chama completar quadrados tá toda vez que tem o nome de grau 2 desse tipo eu consigo nesse caso basta subtrair uma constante mas por exemplo fosse x quadrado mais 6 x mais alguma coisa que dá pra fazer sempre consegue pensar x ao quadrado mais 6 x tem alguma outra constante que fecha unb nome de
nilton perfeitinho x ao quadrado mais 6 x o que tem que vem depois para ser um quadrado perfeito 9 porque é sempre a mais b o quadrado e ao quadrado mais dois saber mais ver o quadrado então tenho x ao quadrado mais 6 x wire x e ali os 6 x é 12 a bené então vai ser 2 x alguma coisa 6 x 2 x alguma coisa essa coisa 3 e ele vai ser o quadrado então nesse caso aqui como é que eu posso pensar x ao quadrado mais 4 x que é o cara que
falta para completar o quadrado perfeito x ao quadrado mascotes mais lembra que esse aqui está x 2 é dois mais quatro né então isso aqui eu consigo escrever como sendo seis vezes a primitiva estou fazendo nada que não seja puramente algébrica aqui né x ao quadrado mais 4 x mais quatro que está faltando para dar certo 9 o treze eu quebrei com 429 certo e aí muito bem isso aqui vai numa direção boa tudo bem tudo feito de caso pensado para funcionar dúvida pode ser por exemplo é que fosse x ao quadrado mais 4 x
mais um que eu ia fazer eu ia somar 3 e subtrair 3 então é ficar x mais o quadrado menos três nesse caso ficou mais ainda bem se não muda tudo tá que dá pra fazer a gente sabe alguma primitiva que tem uma cara de uma coisa ao quadrado mais constante um denominador aqui você sabe quanto que é essa aqui a gente sabe quanto vale a primitiva de 1 sobre o mainz ao quadrado então eu tenho que fazer vou tentar isso aqui está quase lá né a diferença é que não tem um número um aqui
e aqui tem um fator linear elevada ao quadrado o que eu vou fazer vou brigar um pouquinho essa expressão para tentar deixar ela com aquela cara de qualquer jeito bom deixá la com aquela cara pra começar é isso aqui vira um número 1 a 1 e como é que eu posso fazer isso virar um número 1 sem bagunça muito a vida da integral puxa 19 em evidência se você quiser então puxando nova evidência ele vai sair da integral eu vou poder escrever isso como sendo de x sobre x + 2 ao quadrado sobre 9 mais
um certo esse sobrenome eu posso jogar lá pra dentro do paredes e ele vira 1313 mais bonitinho bom e agora está com uma cara muito muito muito boa como é que eu faço isso vai virar daquele jeito mas uma mudança de variável chama 'o de x mais dois sobre três então se o for igual à x mais dois sobre três quem que deu quando teria visto em relação às chances de um terço também então fazendo essa mudança de variável só que vai ficar seis nomes que de x 3 deu ao quadrado mais um bom sabemos
o 3 pela forma integral quanto que vai dar das seis sobre três chama 2 vai ficar duas vezes à tangente de u mas a constante quem é um mês mais dois sobre três então isso a 2 argenti x mais dois sobre três mais uma constante de integração acabou médio né então voltando e isso é o dois asteriscos né dois asteriscos usei para cálculo integral do asterisco então isso aqui o que quer na verdade x - o asterisco quem é o asterisco asterisco é esse blog x ao quadrado mais 4 x + 13 + o dois
asteriscos mas tem um menu só não pode esquecer na a ficar menos 2 x mais dois sobre três mas a constante ao menos entrar no carro é preciso então é uma coisa bem trabalhosa mas você tem um algoritmo né pegou porém o cara lá foi racional você sabe exatamente o que fazer a seguir ao de cima o formato de baixo de vide para deixar no jeito pra aplicar a teoria já veio menor o fator denominador estuda utilidade das raízes ou não a existência dessas raízes tá então tem um algoritmo de mora em um exemplo pra
você fazer uma lista e a boa notícia que o melhor que uma boa noite você acha que tem chance de eu te perguntar isso um lugar que tem umas cinco questões para resolver os olhos muito profundo é só uma se você não sabe se tira zero sabe tinha idéias não é legal né então né esse tipo de coisa é bom você saber que existe mas é claro que a gente em cobra o próprio frações parciais dominique deverá agradecer tudo que precisa mais infrações parciais é claro que a gente cobra em prova a gente não cobra
esse caso que é muito chato beleza com isso a gente já tem condições plenas de resolver todas aquelas primitivas da da lista já aquelas 77 acho que não né 77 primitivas com essas técnicas que a gente não dá pra fazer todas depois eu vou ensinar mais uma técnica que assim é um chama aquele enfeites e põe em cima do bolo não serve pra nada mas é assim facilita resolver um ou dois exercícios é uma técnica extra mas é promete um bônus assim tá mas dá pra fazer tudo e é bom você fazer todos eles para
sentir as dificuldades treinar etc etc curiosamente quando você chega lá no cálculo 3 a lista 0 que nem a gente tem a lista 0 de cálculo um analista 0 de cálculo três são exatamente 77 exercício é do tipo é o que você tem que saber tá pra seguir no curso vamos ver a parte mecânica é o que corresponde a parte mecânica daquele curso legal bom depois a gente volta dessas técnicas de primitivas especiais etc eu acho que como é que a gente está de tempo você começa o assunto ante 51 15 minutos está então a
gente pode usar o chamar volumes áreas e cumprimentos tá a gente pode usar o que a gente está aprendendo agora quer dizer integral de funções em uma variável para calcular o volume de certos tipos de sólidos tá sólidos que tem uma certa simetria rotacional o que eu quero dizer exatamente a gente consegue calcular sólidos que são obtidos girando o gráfico de uma certa função em torno do eixo x ou em torno do eixo y é tão exemplo bem simples qual a função mais simples e é que a gente conhece o som constante beleza não pega
uma função constante na súmula como el gráfico dela isso aqui se eu pegar no intervalo a b isso aqui me dá um retângulo seu giro esse retângulo em volta do eixo x o que eu vou obter um cilindro então eu posso usar o fato de eu saber calcular essa área para determinar o volume de cilindro de rotação aqui tá se eu roubar isso aqui em volta do eixo y que eu vou obter um anel não cilindro vazado com outro cilindro dentro dá pra gente tentar calcular esse volume via integrais de uma função de uma variável
no cálculo 3 você vai desenvolver uma técnica para calcular volumes de sólidos de qualquer tipo sólidos que você saiba calcula o volume e volume existe a gente consegue calcular de algum velho por enquanto a gente não está restrito a sólidos que são determinados pela rotação de gráficos de funções em torno de um dos eixos da até mas isso a gente não vai fazer mas é uma coisa muito interessante você tentar fazer a ponte entre as disciplinas que está aprendendo né está vendo coisas de álgebra linear se você quisesse tem um gráfico de uma função se
eu roubar ela em torno de outro eixo que não seja o eixo x o eixo y dá pra fazer alguma coisa eu quero pega o gráfico de uma função que o volume do sólido obtido rotacionando em torno de outro eixo fazer isso você tem um eixo panahi 2 se você tem um eixo tem um vetor que dá a direção deseja se acham caro ortogonal ele e portanto vai ter uma base ortogonal para o r2 você tem a base canônica que da oea x y e outra base você tem um gráfico da sua função é pontos
da forma x vírgula fdx são as coordenadas dele na base canônica reescreve esse vetor x do fx nessa outra base e aplicar essa mesma técnica então você consegue fazer usando uma mudança de base e rotação e torno de qualquer um pode ser que a função da nova fórmula 1 seja tão bonitinha contrária antes pode ser que a nova forma não deu gráfico de uma função em geral não dá então gostaria de algumas outras coisas mas dá pra fazer sempre importante ligados a matérias que a gente está aprendendo então vamos lá a ideia primeira é que
a gente vai ter o seguinte só pode ter uma função integrável definida no intervalo a b por exemplo contínua vai para garantir a função contínua que minha intenção é rotacionar esse gráfico a figura vai virar tridimensional certo vou sair da lousa eu vou tirar isso aqui em volta do eixo x isso vai produzir um sólido né de que tipo uma coisa mais ou menos assim vai falta de simetria puramente dá pra imaginar o que aconteceu nessa girou virou um vasinho ali alguma coisa desse tipo tá certo que a minha intenção é calcular o volume de
ensino de sólido como é que a gente pode fazer isso pensar em termos da soma de rima né quando o qual prova integral embaixo da função que eu tinha integral de fx o intervalo a b a área embaixo desse gráfico né e como eu poderia então o que eu estava fazendo intuitivamente era somar áreas de pequenos retângulos do acerto não era isso integral de riman retângulos diminuindo a base cada vez mais para tentar o rock como é que eu poderia obter uma aproximação para esse volume poderia aproximar esse volume pelo cálculo do volume de pequenos
cilindros do mesmo tipo como pega os retângulos doutor soma de rima tudo bem você e todos nós somos irmãos e hoje esses retângulos que obtenho cilíndricos né então a idéia é mais ou menos essa cirurgia é um cara desse tipo você vai obter um pequeno cilindro e a idéia é fazer o que somar o volume de cilindros pedindo que a altura deles tender para zero como que você calcula o volume de cada um desses cilindros que é o volume de um cilindro a área da base vezes altura né então quem que é a altura de
um cilíndrico desses na soma de rima altura o delta tem e quem que é o raio é altura o valor da função em algum naquele ponto sei que a gente escolher da soma de ri muito certo então o que a gente vai fazer qual vai ser minha sombra de renan que vai determinar esse volume à área da base da circunferência quanto vezes o valor da função do intervalo seino pontos e ao quadrado vezes delta tem então soma de rima que a gente vai estar olhando é uma coisa desse tipo e vezes fdc ao quadrado pergunta
essa soma de rima há uma certa parte são pequenos gerou os pontos têm uma certa a escolha dos pontos sem essa soma de rimas eu tomar o limite com a norma da parte não tem medo prazerosa converge o limite ou seja essa função qual é a função que eu sou essa soma de renan a soma de renda de qual função é a função que estou calculando é a função da constante pi fez fdx ao quadrado relativa participei escolha do serviço o certo é isso pergunta é essa função aqui é uma função integrável sim porque se
a f é integrável né pega contínua para facilitar a cef é contínua é o quadrado também é contínuo portanto é integrável toda função continua integrado então isso aqui é uma função integrável portanto esse cara que se eu tomar o limite e vai convergir para uma certa integral e integral chamado de volume tá bom então quem é o volume do sólido de rotação nesse caso é integral de até b de pi vezes fdx ao quadrado deixe se consiga determinar o sólido volume de solo exemplos vamos fazer dois exemplos bem simples se der tempo 3 vai coisas
que a gente sabe calcular o volume e que se encaixam nessa situação qualquer caso que a gente sabe qual o volume mais simples um cilindro como é que o volume do cilindro eu consiga obter o cilindro como rotação de uma função que eu falei a gente pega função constante né então pega fdx constante igual a r tá isso vai produzir um gráfico desse tipo se eu pegar no intervalo a b quando rotacional obter exatamente um cilindro vamos calcular através dessa forma para ver se bate com a área do cilindro que a gente quer mesmo então
a quem que seria o volume integral de até b dp vezes é o quadrado de xx quando que vai dar isso integral de apb pf é constante igual r é o quadrado de x você concorda que tudo é uma constante saída integral enquanto que fica então integral e integral de até da função constante igual a um vale - a tudo bem então que deu isso exatamente a área da base pi vezes o raio quadrado alto bateu essa função não for constante ela for uma reta que passa pela origem o que a gente obtém um cone
sabe calcular o volume do coni um terço da área da base vezes altura vamos ver se bate então pega fdx igual a uma constante tá que vai te dar isso uma reta de coeficiente angular a que passa pela origem na hora que eu vou acionar obter exatamente um cone né enquanto o volume desse ícone vamos dizer que esse ponto aqui é o ponto h que vai mexer altura do conde né então o volume desse ícone o que seria integral de zero até h da fonte vezes a função o quadrado bem quanto que vai dar essa
coisa aqui e say say x ao quadrado de 0h quando que dá isso com a primitiva de x quadrado ao cubo sobre três calculado no hm 10 vai dar deu certo isso é o volume desse ícone enquanto que a área é também estranho aparentemente né enquanto que é essa altura que vai ser o raio da base né se a função fx é igual à x quanto que esse valor à vezes h tudo bem então isso aqui eu posso escrever como sendo pe a vezes h ao quadrado sobre três vezes h sob três para ficar bem
na área da base vez altura sobre três então bate com a forma do culto ao outro que a gente sabe o volume esfera eu consigo produzir fera como rotação de algum gráfico como é que se pode pensar numa esfera a partir de uma rotação se eu tirar uma circunferência em torno de um eixo que passa pelo centro obter esferas só que o seu gráfico de uma função então o que a gente faz é da minha esfera foi exatamente exatamente isso 4 - ao quadrado porque se está com raiva dois né então vamos pensar num caso
mais geral sim né se você tem uma esfera de raio é você tem raio r eu vou pegar a equação da circunferência metade que seria quase passando a circunferência de hardware x2 mais opções dois igual é enquadrado para pegar uma função que eu vou pegar quem a raiz positiva por exemplo então raiz quadrada de r ao quadrado enfatizou quadrados de solo y en se pegando sua metade de cima tá certo então quem seria o volume é integral de menos r até r jipe vezes essa função ao quadrado deixe-se certo quando eu tirar essa mesma conferência
obter essa atmosfera de raio é tem que fazer essa conta quanto que da piccola fora integral de - rtr ele vai ficar e vezes o raio quadrado né escreveu isso pipo lá fora tem meu jeito de escrever isso aqui você pode ter um sistema integral de menos r até gera um quadrado de x - integral de r - rtr ao quadrado do x bom rock sabe calcular cada uma delas sabe quanto que vai daqui a primitiva é é o quadrado vezes x vai dar r ao cubo - - é o cubo sobre 32 ep vezes
2 é o cubo sobre três é que vai dar chances ao cubo sobre três se faz a continha tá quente não tem mais tempo você fizer toda a conta juro para vocês aqui vai dar quatro textos de pizarro tá bom a gente consegue ao povo onde na esfera outras coisas que você pode fazer pega a região presa entre dois gráficos e rotaciona consegue fazer isso por exemplo calcular o volume de um cilindro vazado ou você pode pegar um cone e vaza com cilindro é fácil porque você tem a fórmula dos dois poderia calcular vice integral
vai fazer o volume de fora - o volume de dentro não precisa ser uma coisa as retas para quaisquer das funções você tem uma peça que você precisa calcular que ela é composta pelo corte se pega um cilindro e como uma parábola de dentro dele caso alguma peça qual é o volume de solo você sabe calcular o volume do cilindro - o volume da parábola que você tem pelo outro em torno do xx dá pra fazer tudo isso de trabalho nesses exercícios mais pra frente e pra próxima aula que a gente vai fazer vamos ver
como calcular o volume de um sólido pegando um gráfico rotacionando em volta do eixo y e depois eu aprendi também a calcular a área superficial né foi quando eu volto só isso é que gera uma superfície tem uma certa área pergunta natural eu consigo calcular essa área com cinco então vou calcular a área de rotações em volta do eixo x a área de rotações em volta do eixo y em outra coisa que é de interesse calcular e qual é o cumprimento dessa curva né se eu pegar esse gráfico e esticar ele é uma linha retorcida
né você pensa que já pensa em título finalmente gráfica uma linha que o leitor se você esticar quanto que mede isso com que vai ter vez com o derivado né é derivado é o que diz o quanto gráfico importa então vai na hora que for calcular cumprimento vai aparecer dentro da fórmula 1 é filhinho ali a gente faz tudo isso na próxima 8 e aí faltou só mais um ou dois tópicos a gente termina matéria tá bom vamos discutir bastante desses exercícios vão fazendo a lista por favor tá tão brigado e até sexta
Related Videos

25:36
Cálculo I - Aula 29 (1/3) Sólidos de Rotaç...
Canal USP
11,497 views

32:28
INTEGRAÇÃO POR FRAÇÕES PARCIAIS #21 ✅
Prof. MURAKAMI - MATEMÁTICA RAPIDOLA
159,234 views

jazz lofi radio 🎷 beats to chill/study to
Lofi Girl

26:35
Cálculo I - Aula 1 (1/3) - Panorama do Cál...
Canal USP
429,772 views

Classical Piano & Fireplace 24/7 - Mozart,...
Odd Eagle

28:11
Cálculo I - Aula 26 (3/3) Exemplos de subs...
Canal USP
12,202 views

28:21
Introdução ao Cálculo Diferencial e Integr...
Professor Possani
966,639 views

28:52
Cálculo I - Aula 25 (1/3) Integral de Riem...
Canal USP
45,766 views

30:31
Cálculo I - Aula 27 (3/3) Mais exemplos e ...
Canal USP
9,632 views

14:07
Me Salva! INT37 - Integral por Frações Par...
Me Salva! ENEM
572,481 views

23:57
Cálculo I - Aula 34 (1/3) ) Integração - o...
Canal USP
9,256 views

25:29
Cálculo I - Aula 29 (3/3) Comentários gera...
Canal USP
4,986 views

27:53
Cálculo I - Aula 29 (2/3) Sólidos de Rotaç...
Canal USP
5,938 views

27:35
Cálculo I - Aula 32 (1/3) Funções dadas po...
Canal USP
6,074 views

33:03
Cálculo I - Aula 30 (1/3) Cálculo de algum...
Canal USP
5,538 views

15:07
Trump's Rambling Lying Meet the Press Inte...
Jimmy Kimmel Live
1,702,747 views

14:20
🟢 PASSO a PASSO PARA CALCULAR INTEGRAL IN...
Matemática - Prof Reginaldo Moraes
687,829 views

16:06
The Greatest Mathematician Who Ever Lived
Newsthink
458,839 views

1:38:06
Best Fails of the Year | Try Not to Laugh ...
FailArmy
5,488,993 views