QUESTÃO LINDA DE ÁREA: VÁRIAS PROPRIEDADES EM UMA ÚNICA QUESTÃO .

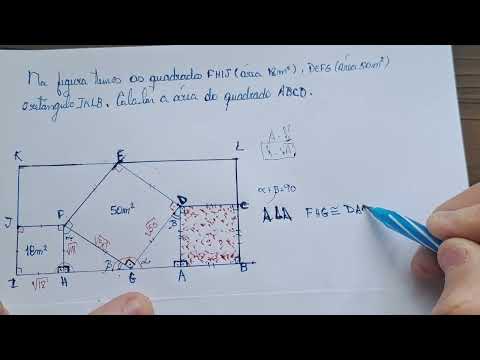
Olá pessoal sejam todos muito bem-vindos a mais uma vídeoaula eu sou o professor Márcio e trago para vocês mais uma questão de geometria plana para nós acharmos a área uma área desconhecida aqui uma área pintada aqui na nossa figura a questão diz o seguinte Na figura temos os quadrados f h e j de área 18 m qu de FG de 50 m qu e o retângulo e o retângulo I LB e IB calcule a área do quadrado a c d ok pessoal eu comecei a resolver essa questão porém como eu tô próximo do aeroporto aqui

às vezes acontece o helicóptero Passa muito próximo aqui faz barulho isso aí eu eu acho acabei de falar e não é proposital que eu que eu gravo essas aulas exatamente no horário de helicóptero é porque eu estou sem a minha luminária de mesa à noite geralmente eles não decolam E então [Música] Eh eu acabo fazendo essas aulas nesse horário e acaba coincidindo com o horário dos helicópteros vocês me perdoem aí o barulho externo que a gente não tem muito controle sobre isso Aliás não tem controle algum bom eh eu comecei a resolver como eu disse

eu e resolvi recomeçar a questão antes de começarmos a novamente a questão eu gostaria de pedir a você caso você não seja inscrito na na no nosso canal se inscreva no canal Aperte o Sininho das notificações para você receber todos os vídeos que a gente postar aqui e caso faça sentido para você a videoaula e você entenda sobretudo deixa o seu like e deixa o seu comentário ou Suas críticas ou uma maneira diferente de resolver a questão Isso vai ser muito interessante pro nosso canal aja Vista que o YouTube vai entender como sendo relevante este

canal eu agradeço antecipadamente bom eh eu comecei fazendo o seguinte como o i jfh foi isso que ele disse Exatamente é um quadrado e a área dele mede 18 m qu duas coisas a gente tem certeza absoluta aliás três né duas coisas a gente tem certeza três evidentemente que os lados são todos iguais que os ângulos internos também t a mesma medida e mede 90º cada um E que a área dele foi dada informada 18 m qu logo a gente conclui que o lado nada mais é do que a raiz quadrada da própria área dada

aqui então Ó o lado aqui é √1 assim como este lado também é √1 aqui É √18 aqui é √18 tudo bem E o mesmo raciocínio a gente vai usar para este quadrado que tem área de 50 m qu o lado dele os lados desse quadrado são todos iguais os ângulos medem 90º é importante a gente destacar eles né então o lado nada mais é do que a raiz quadrada da própria área dada aqui haja vista que a área de um quadrado né a área de um quadrado é igual ao lado ao quadrado logo o

lado nada mais é do que a raiz quadrada da área Ok Isso é bem tranquilo de entender feito isso eh perceba que este lado aqui ó esse esse triângulo aqui ó a gente pode provar que ele é retângulo Por que que ele é retângulo porque veja se eu tenho um ângulo de 90º aqui E esse ângulo aqui é um ângulo raso evidentemente que este ângulo somado com este dá 180º e 180 Men 90 né do do quadrado O que falta para completar o 180 evidentemente este ângulo aqui é um ângulo de 90º tudo bem beleza

feito isso eu vou e chamar este ângulo aqui ó de ângulo alfa e este ângulo aqui ó de ângulo Beta tudo bem perceba que alfa + beta é 90º haja vista que a soma dos ângulos internos de um triângulo qualquer sempre vai dar 180º se eu já tenho 90 quer dizer que ala + Beta é 90 agora eu queria que vocês prestassem atenção neste nosso ângulo aqui ó que é importante para nós que ângulo é esse é um ângulo raso ângulo de 180º perceba que você tem 90 e aqui você tem o ângulo Beta né

esse ângulo 90 mais Beta mais esse ângulo tem que dar 180 como eu já tenho 90 aqui e eu sei que al mais B é 90 se aqui é Beta aqui evidentemente que vai ser Alfa algo mais importante também que é interessante a gente destacar que como o esse esse quadrilátero é um quadrado né quadrado tem as medidas Todas Iguais né os lados todos iguais né e os ângulos também tem a mesma medida 90º então perceba que este ângulo é 90 e este ângulo pelo mesmo raciocínio daqui este ângulo também é 90 Ok note o

seguinte se eu tenho um ângulo de 90 e tenho Alfa aqui efetivamente este ângulo será Beta e professor estamos diante de um triângulo de dois triângulos semelhantes eu digo mais além de semelhante eles são congruentes porque veja a hipotenusa deste triângulo aqui é 50 √50 a hipotenusa deste triângulo aqui também é √50 o ângulo com a hipotenusa é alfa o ângulo com a hipotenusa no outro triângulo também é Alfa perceba que o outro ângulo também é Beta e também no triângulo ADG o outro ângulo também é Beta pelo caso lado lado ângulo lado Opa ângulo

perdão ângulo lado ângulo pelo caso ângulo lado ângulo lado ângulo Então eu tenho o ângulo Alfa ângulo Alfa tem o lado que é a hipotenusa também tem a hipotenusa igualzinho tem o ângulo Beta e tem o ângulo Beta então pelo caso ângulo lado ângulo esses dois triângulos são congruentes eu posso dizer que D perdão f h g é congruente ao triângulo d a g certo além de semelhante eles são e é muito melhor a gente visualizar el sendo eh congruente por quê Porque ele sendo congruente os lados opostos aos seus ângulos que são homólogos né

que são iguais também tem a mesma medida então perceba [Música] eh Antes de nós calcularmos aqui efetivamente vamos voltar ao triângulo fhg fazendo isso vamos aplicar o teorema de Pitágoras e vamos encontrar este lado o que que diz o teorema de Pitágoras colocando de uma forma genérica aqui o quadrado da hipotenusa é igual a soma dos quadrados dos catetos tá a hipotenusa é o a quadrado que eu estou dizendo aqui então a hipotenusa no nosso triângulo ali é a raiz 50 evidentemente eu tenho que elevar ao quadrado pelo teorema de Pitágoras aí o b Vamos

colocar como sendo a ra 18 a quadrado e o c é aquele valor desconhecido que eu quero encontrar feito isso eu aplico aqui eu ó eu posso cancelar a o expoente 2 com o radical de índice do né é a mesma coisa que escrever isso aqui na forma de potência com expoente aono o expoente vai dar 1 então aqui ó 50 é igual a 18 ó cancelei o radical com 2 + C Quad daí nós temos que C qu vou passar o 18 pro outro lado é 50 - 18 C qu é igual a [Música]

32 50 - 18 10 Men dá 2 32 a c é ra 32 novamente eu não vou me importar em tirar aqui aqui é ra 32 tá ra de 32 calculamos aqui concluímos que esse triângulo é congruente a este triângulo hja Vista que aqui é Alfa tem a hipotenusa 50 e tem um ângulo Beta aqui também tem um ângulo Alfa a hipotenusa 50 e um ângulo Beta caso ângulo lado ângulo também também poderia ser ângulo lado ângulo oposto poderia ser também ó ângulo lado ângulo oposto ângulo lado ângulo oposto também poderia ser esse caso de

especial do triângulo retângulo bom feito isso Perceba o seguinte no triângulo isósceles nós concluímos isso os lados que T Como eu disse anteriormente os lados que TM ângulos homólogos eles têm né os os os lados opostos a ângulos homólogos eles são exatamente iguais nos dois triângulos então ó quando você olha pro ângulo Alfa você enxerga qual lado a ra 32 do mesmo modo que olha só no ângulo Alfa aqui ó nesse outro triângulo que é congruente né no triângulo ADG quem o ângulo Alfa está enxergando está enxergando o lado do quadrado logo o lado do

quadrado mede o que ra de 32 máo mas nós não vamos tirar essa raiz quadrada aí fatorar isso não precisa por quê Porque nós não queremos a área do quadrado quer dizer que todo lado desse quadrado mede cada lado mede √32 eu quero a área do quadrado a área do quadrado é o lado ao quadrado então a área do quadrado que eu procuro né vai ser o quê posso até colocar aqui ó a b CD é igual a qu a ra Quad 32 visto que é o lado ao quadrado né então a área do do

quadrado AB CD é exatamente o quê 32 como foi dado em metros né a área é met qu é isso pessoal Note que a congruência de triângulo apareceu ali foi muito importante para nós Eh deduzirmos aí a área calcularmos a área do do quadrado aí que foi pedido Espero que tenham gostado se isso aconteceu deixe o seu like compartilhe deixe seus comentários e se inscreva no canal sobre tudo caso você não seja inscrito até a próxima vídeoaula e bons estudos para vocês