Projeto e Análise de Algoritmos - Aula 13 - Problema do caminho mais curto
6.26k views2947 WordsCopy TextShare

UNIVESP
Projeto e Análise de Algoritmos - Aula 13 - Problema do caminho mais curto de uma única origem em gr...
Video Transcript:
[Música] o [Música] olá pessoal sejam bem vindos à nossa aula número 13 do projeto em análise algoritmos nessa hora vemos o problema de caminho mais curto de uma única origem grafos vamos ver a técnica de relaxamento e vamos ver apenas um algoritmo que faz essa tarefa que o algoritmo de destro suponha que você deseja encontrar o caminho mais curto possível desde o rio de janeiro até são paulo então entra aqui para aqui como é terminar rota mais curta nesse caso a gente pode modelar esse problema como um problema em gráficos você vai ter um grafo
conversa encerrar esta em que os vértices são as cidades e as áreas são os caminhos entre essas cidades se você vai ter um peso nessas tarefas então cada aresta vai ter um peso associado que seria por exemplo nesse caso a distância entre o peso de um caminhão como que vai ser calculado então dá um caminhão p aqui temos um caminho que vai de vencer o avaí eo e terminei ver k vai ser calculado como a soma dos preços de todas as arestas que passam por esses sete meses que seria essa fórmula 1 daqui então temos
que o peso no caminho p essa uma história dos preços das arestas que vão de 90 cm não sou um atleta e sair com lhe dizer um até cá como definimos então o peso do caminho mais curto de seu a tv de maneira genérica a gente vai calcular os preços de todos os caminhos possíveis isso porque assim existe um caminho ou a tv pegamos todos os caminhos possíveis e o atv e calculamos com o que vai ser o mínimo então isso vai ser em tom é definiu como o caminho mais curto desvio antes eo atleta
então não existe um caminho de uma tv essa distância deu à tv mais sedada mas só definirá como infinito tem uma característica importante nos caminhos mais curtos que a subir estrutura ótima está definido aqui nesses lá e depois vamos ver um exemplo do que significa isso seja um grafo g que tem um conjunto levanta e se um conjunto de erez da sombra foi orientado e compensamos isso querem ser ponderado e seja um caminho neste gráfico vamos supor que temos um caminho que segui todos esses vetos e vê uma tv cá se a gente pega um
sub caminho desse caminho vamos supor que pegamos uma parte desse sucesso desse caminho que seria por exemplo esse caminho pj que vai desde 96 atletas e j esses subica minho também vai ser o caminho mais curto dizia a tj se esse caminho daqui era o caminho mais curto deveu à tv cá de maneira sempre vamos ver aqui então é sempre um sobre isso suponha que você conhece qualquer uma o menor caminho do rio de janeiro até são paulo se você já tem isso isso porque esse realmente o melhor caminho do rio de janeiro em são
paulo se a gente pega o sub caminho desse caminho esse caminho também vai ser um caminho mais curto entre essas cidades por exemplo se a gente pega o caminho desde agora tem que tá até são paulo esse caminho aqui esse caminho aqui também vai ser um sub caminho mais curto entre a cidade e agora tem tá até são paulo uma outra característica que precisamos é ver investigar e que acontece quando temos áreas de pressão negativa o carro pode vir a lista de peso negativo sim claro no nosso exemplo anterior que sobre a distância sobre caminhos
entre as cidades a distância não pode ser negativo mas para outros 60 anos poderia ter-se uma distância negativa 1 um peso negativo na verdade nas áreas como nem sempre a descer grafo que temos aqui em baixo os pesos do caminho de caminhos mais curtos não vão estar bem definidos caso assista um ciclo de peso negativo como nesse exemplo de quim aqui temos um ciclo de peso negativo e seria esse de quinta e se a p&g ps cujo valor seria menos dois toda vez que a gente passa por esse ciclo a gente vai ter menos 2
- 2 - 2 - 2 - 2 - 2 se a gente passa infinitamente por ele vai ser menos infinito é então que aconteça com isso a gente não pôde calcular qual que o caminho mais curto quando a gente tem ciclos de peso negativo se um ciclo de peso negativo em algum grafo num caminho de se a tv então vamos definir que a distância desse a tv - infinito existem dois organismos conhecidos para resolver o problema de caminho mais curto de um homem de origem que são o algoritmo de dastan e orgulho de ver na
foto o algoritmo de desta ele vai supor que todos os presos as arestas um grafo são negativos então com ele por exemplo podemos resolver o problema do caminho mais curto de são paulo até qualquer outra cidade do brasil por exemplo né e organismo verma for ele permitem arestas e pessoal negativo no gráfico sim o que ele vai fazer na verdade ele vai verificar se esses em ciclos e caso esses ciclos ele vai detectar isso e vai produzir uma resposta correta para o problema o resultado da busca do caminho mais curto é uma árvore ray sada
no na origem então ele vai mostrar qual é o caminho mais curto desde a origem em ciência a tecnologia verde e acessível a partir desse quem mais a gente já tinha falhado isso antes também quando a gente trabalhava com algoritmos de busca em profundidade em buscas na largura na verdade o algoritmo de busca em largura em gráficos porém nesse caso a gente não trabalhava com os pesos entre é nessas áreas não tínhamos peso nas arestas nesse caso temos é temos um caso do mapa uma distância entre uma cidade e outra por exemplo então o resultado
do do caminho mais curto resolver o problema o caminho mais curto vai ser uma árvore aqui temos um exemplo de um grafo e aqui temos um exemplo das duas possíveis árvores que poderia ser a solução do caminho mais curto para esse grafo estão mostrando se aqui então temos aqui essa árvore que está enraizada em s e ele está mostrando que o caminho mais curto para ir de se ater e passar exatamente porém saretta de si até que o custo e 3 o caminho mais curto para ir dance a tx tem um pessoal de 9 e
ela passa pelo vértice ele passa pela está e ct-e área tx e assim por diante temos uma outra opção que também tem os mesmos valores é um caminho mais curto também mas que passa por outras arestas quem sabe aqui um caminho mais curto de si até 3 o caminho mais curto de se a y r 5 mas ela passa pela área está e citei pela está tem destino certo que os custos são iguais então são duas possíveis soluções para o mesmo problema o estado orismar de weimar for quanto o agora os modais para ele usa
eles usam a técnica de relaxamento eles vão ter que calcular uma estimativa do mapa do caminho mais curto que vão chamar de de dever então em de ver a gente vai aguardar o limite superior sobre o peso do caminho mais curto desde a origem ea tevê início quando não sabemos nada um grafo esse limite superior vai ser infinito não sei qualquer chance de dizer se a teoria é que se qualquer então vou colocar infinito então primeiro vamos fazer a inicialização passou de inicialização que eu acabei de falar como não sabemos nada a estimativa de qualquer
e é o valor do caminho mais curto até cada vez e ver mas ser infinito não sabemos quem são os pais não só colocar mil e sabemos que a instância de origem e se a teoria inss serão a gente já está no próprio vértice agora então vamos ver o passo de relaxamento esse passo de relaxamento consiste em verificar se podemos melhorar o caminho mais curto para ver encontrado até agora pela passagem através de u se acontecer isso vamos atualizar a nossa estimativa de e também que o pai é então como key é feito isso se
a gente tem uma estimativa a tba tv de s isso porque a gente tem é se a gente tem aqui a gente tem uma estimativa de qualquer instância passado por outros vezes até 90 cv isso porque ela é de dever e agora a gente vai verificar se passado por uma agente consiga melhorar isso não tá agora vamos ter a estimativa até u vamos ver se um samba a esta o v a gente consiga melhorar essa estimativa vamos supor que eu sei que o dever de 20 eu sei que o dedé eo é tri é vou
colocar um número menor de 15 e à distância entre um e vem e 3 seu olho aqui então passado por um eu posso melhorar a minha estimativa a tv agora vai ser 18 no lugar de 20 isso é o que está sendo feito aqui se a estimativa que eu tinha a tv é maior que a estimativa que eu tenho até o mais o pessoal da arysta o v então eu posso melhorar a minha estimativa como esse valor e aí a polícia que em que o pai de ver o pai de ver eu seja a gente
está atualizando quem que o pai de ver agora passava pelo para chegar em ver esse é o processo de relaxamento então quem quer faz valores mobiliários da extra ele vai calcular qual é o caminho mais curto tem uma única origem em um algoritmo orgulhoso nesse caso ele só permite que as arestas tenha peso positivo em consequentemente não vai ter ciclos de peso negativo ele não vai precisar se preocupar com isso além disso o tempo de execução o curso de processamento dele é inferior ao coritiba for que um pouquinho mais genérico que ele pode se trabalhar
com arestas negativas valores modais trabalha com dois conjuntos evets o conjunto esse que são os doentes cuja distância para arraes shea conhecida é ou seja é a definitiva e um conjunto vermelho não sei se é que o conjunto de veto e sem que a distância é conhecida ainda é uma estimativa provisória seja apenas em estimativa não sei se é exatamente isso não para isso o algoritmo vai utilizar duas estruturas o ec que vai ser um conjunto de eventos cuja distância é definitiva e o que para para guardar os 76 quando estância provisória é esse que
vai ser uma filha de prioridade mínima e aqui temos então o pessoal do código do algoritmo de da strans ele usa o algoritmo que faz a inicialização das estimativas e o relaxamento das estimativas aqui para ver o funcionamento desse terrorismo vou mostrar aqui um exemplo então suponho que temos um grafo com cinco vértice o vertis e é ct x e y en sei que estão aqui também nessa tabela em baixo e temos a qualquer o peso de cada uma das areias neste gráfico também queremos saber qual é o caminho mais curto desse ato até todos
os verdes e atingíveis a partir desse aqui nessa tabela vamos guardando qualquer estimativa que são os pais que vai ter a fila de prioridades e o que vai ter um conjunto esse certo então no início o primeiro que vai ser feito vai ser a um passo de inicialização no momento inicializar a gente vai colocar que a nossa estimativa é infinito para todo mundo os pais é exceto para o noé se que a instância dsts e terceiro quem são os pais todo mundo uniu a gente não sabe quem é o pai na área da resposta e
aí depois a gente vai ver é inicializar o conjunto e se com vazio e o conjunto que com todos os répteis que está aqui mostrado com 11 chega e aí depois enquanto a filha não esteja vazia o que vai ser feito continuamos aqui enquanto a filha não seja macia a não ser o mínimo do conjunto que o mínimo do conjunto que nesse caso é aquele que tem a estimativa melhor nesse caso o fcs vamos colocar em tom e se esse evento disse vamos colocar no conjunto esse maiúscula esse aqui ok o próximo passo é então
fazer um relaxamento das arestas o que vamos nos perguntar nesse passo será que podemos melhorar o caminho mais curto att que são um dos grandes ideais de acidentes a esse é encontrado até agora pela passagem através desse sim a gente tem estava infinita a nossa estimativa passando por esse a gente tem um caminho mais curto que o tamanho 10 certo faremos o mesmo com o outro vértice que a gente sente a ele que o y e aí perguntava será que podemos melhorar o caminho mais curto até este não encontraram até agora pela passagem desse sim
a minha estimativa é infinito e agora eu tenho uma estimativa de 5 passando por pelo ipc s então vamos atualizar esses valores aqui então temos agora que os valores foram atualizados para 5 e 10 aqui também vamos atualizar nossa tabela a nossa estimativa mudou e agora o próximo passo é original ou extrair um mínimo da da filha que tem o valor mínimo da fila na filha eu tenho te x y e c que tem um valor mínimo é o y então vou extrair o y e vou colocar ele no conjunto e se estou colocando aqui
no conjunto e se depois vamos passar de novo passo de relaxamento no passo do relaxamento a gente vai verificar todos os dentes adjacentes à distância definitiva mínima até o efeito senão já sabemos que cinco que agora vamos ver os recentes certo então será que podemos melhorar o caminho mais curto para quem são os agentes então os recentes vão ctx ec x e certo será que podemos melhorar o caminho mais curto para ter encontrado até agora pela passagem através da y então vamos lá se passamos por aqui será que podemos melhorar a instância a att sim
se a gente passa por esse caminho aqui vamos a ter uma distância menor que vai ser oito o mesmo perguntamos para x será que podemos melhorar o caminho mais curto para a x encontrado até agora pela passagem através de y se a gente vai por aqui vamos ter uma distância de 5 mais 93 se que o mesmo será que podemos melhorar o caminho mais curto atc sim a minha estimativa é infinito se passamos por isso não vou ter cinco mais 271 então vamos atualizar todos esses valores na tabela então vou ter a minha estimativa att
mudou que em 2008 a tx mudou que 14 e até segunda o q7 e assim continuamos e agora vamos perguntar quem é o menor elemento que está na nossa filha ok é que termine estância menor estimativa menor é um vai acontecer colocámos em tom e vai acontecer no conjunto é esse ok e agora temos a distância definitiva a gente já sabe que a distância mínima até o fcc e 7 e aí continuamos com os vizinhos ele para ver se podemos melhorar o caminho mais curto e aí nós perguntamos será que podemos melhorar o caminho mais
curto para a x encontrado até agora pela passagem através de z então estamos aqui a gente está aqui ea gente tenta usar tenta chegar em x usando esse areia aqui será que o valor melhorar a estimativa do x fica melhor então temos sim passamos por aqui 17 + 6 3 6 3 e melhor de 14 é então vamos mudar o valor dele foi mudado para 3 se o próximo passo vamos tirar o elemento que o elemento menor com esse motivo o menor da fila que o vento e ct colocamos ele no conjunto e se verificamos
já sabemos a verdade é que ela está a ser definitivo a mínima até 2078 verificamos sujacente sair perguntando será que podemos melhorar o caminho mais curto para x encontrado até agora pela passagem através de t então se a gente olha aqui se os amuos pensar esta é que é a chegar em x será que a estimativa fica melhor fica vai ficar 8 mais 19 e aqui há a exigência não se machuca era 3 então melhorarmos a nossa estimativa o que agora é 9 finalmente o o o vértice único vai dizer que está na fila eu
x quem ontem vizinhos não têm mais nada então já sabemos que a estância definitivo a miníma de 96 x 109 e então por fim acabamos com esse evento e já sabemos coloquei-a a nossa árvore está a mostrar aqui então a a nossa água e responsa em saber que já sabemos quais são as distâncias mínimas de cada vez e na verdade a partir do fcs até todos os 86 atingíveis a partir desse a distância mínima de 100 a y e cinco de distância mínima de si até e 8 dez efe a x-9 dse c e 7
c e as arestas pelas quais temos que passar para as para chegar nesse nosso está marcado aí na árvore no vermelho bom essa foi a nossa aula número 3 se sobre o algoritmo de da estrada principalmente espero que vocês tenham gostado [Música] [Música] [Música] [Música]
Related Videos

22:16
Projeto e Análise de Algoritmos - Aula 14 ...
UNIVESP
14,363 views

25:44
Algoritmo de Prim - Árvores Geradoras Míni...
Aulas de Computação
11,767 views
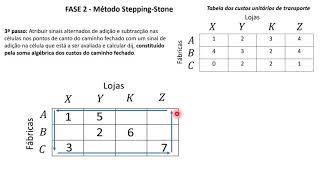
22:37
Algoritmo de Transportes - Método Stepping...
INDUSTRIAL 21
6,252 views

58:12
MIT Introduction to Deep Learning (2023) |...
Alexander Amini
1,986,588 views

37:20
AULA PATOLOGIA DE DOENÇAS GENÉTICAS - I
Alvaro Galdos
3,275 views

21:27
Ergonomia - Aula 01 - Conceitos Básicos e ...
UNIVESP
127,405 views

48:20
EPIDEMIOLOGIA
Medcel
158,101 views

29:56
Complexidade e Classes de Problemas em Oti...
Pedro Munari
14,840 views

25:41
Redes de Computadores - Aula 01 - Introduç...
UNIVESP
413,137 views

29:46
Física Quântica – Aula 01 – Breve História...
UNIVESP
511,639 views

21:06
Bioquímica - Aula 01 - Conceitos básicos
UNIVESP
226,197 views

16:54
Introdução à Engenharia - Aula 1
UNIVESP
337,028 views

22:42
Engenharia de Software - Aula 01 - Modelos...
UNIVESP
287,123 views

16:04
AFINAL, CADÊ O ATAQUE DO IRÃ CONTRA ISRAEL...
Professor HOC
286,424 views

17:25
Estrutura de Dados - Aula 21 - Árvores AVL
UNIVESP
40,641 views

29:48
Logística – Aula 01 – Logística e Cadeia d...
UNIVESP
196,709 views

28:38
Ciência dos Materiais - Aula 01 - Por que ...
UNIVESP
216,655 views

1:07:58
MIT 6.S191: Convolutional Neural Networks
Alexander Amini
60,572 views

59:31
Transtorno Bipolar e Depressão - Lidando c...
Abrata
454,345 views

Jornal da Cultura | 20/08/2024
Jornalismo TV Cultura